数学建模——粒子群优化算法(PSO)【有详细样例 + 工具:matlab】(万字总结)
文章目录
- 一、粒子群优化算法(PSO)是什么?
- 二、粒子群优化算法有什么用?
- 三、粒子群优化算法的适用范围?
- 四、算法简介(有助于理解)
- 五、算法流程
-
- 第一步:初始化
- 第二步:计算粒子的适应度
- 第三步:更新个体极值与全局最优解
- 第四步:更新个体的速度和位置
- 第五步:设置终止条件
- 六、matlab代码实现
- 七、运行结果
-
- 1、各粒子的初始状态位置
- 2、各粒子的状态位置变化图
- 3、各粒子的最终收敛位置
- 4、收敛过程
- 七、粒子群优化算法的使用流程图
- 八、粒子群优化算法的特点:
- 九、拓展知识
- 十、总结:
- 十一、参考附录:
敲到码穷处,望尽天涯路。
数学建模系列文章——总结篇:《数模美一国一退役选手的经验分享[2021纪念版]》.
一、粒子群优化算法(PSO)是什么?
粒子群优化算法(Particle Swarm optimization,PSO) 是一种通过 模拟鸟群觅食行为 而发展起来的一种 基于群体协作 的 随机搜索 算法。
设想这样一个场景:一群在随机搜索。在这个区域处处分散着虫子。所有的都不知道最集中的地方在哪里。
但是它们知道各自目前位置的虫子密度 和 其他鸟周围的虫子密度。那么找到目标地点的最优策略是什么呢?
最简单有效的策略就是:
1. 众鸟一起去搜寻 目前在虫子密度区域最大的鸟 的周围区域。
2. 根据自己飞行的经验,来判断虫子密度最大的区域的所在。
算法核心思想:PSO的基础是 信息的“社会共享”
二、粒子群优化算法有什么用?
和蚁群算法、遗传算法类似,包括粒子群算法,这三者都属于 无约束 的优化算法,属于全局搜索算法,是 启发式 算法。
它只能够得到 全局最优的近似解 ,可能得不到全局最优解。
这些算法可以用在全局路径搜索、网络路由规划、寻找复杂函数的最值点等应用,比如 TSP路线搜索。
三、粒子群优化算法的适用范围?
该算法可以用在,关于 大数据、复杂度高、目标函数复杂的 要求要解出最优值 的问题中。
也可将其作为辅助模型来搭配主流模型,将两个模型的结果做一个对比、分析。看看智能优化算法与主流模型的差距。
四、算法简介(有助于理解)
在PSO中,搜索空间中的每一只鸟 对应 优化问题的每个解。我们将 “鸟” 称之为 “粒子” 。
所有的粒子都有一个 “随身携带” 的属性,即需优化的目标函数所计算出的适应值(fitness value)。每个粒子还有两个属性一个是飞翔的速度,另一个是当前的位置。
然后粒子们就追随当前的 最优 粒子,动态地在解空间中搜索全局最优解。
五、算法流程
我们以两个例子(第2个例子在 十、拓展 一栏)作跳板,从 1维 到 多维 , 由易到难。
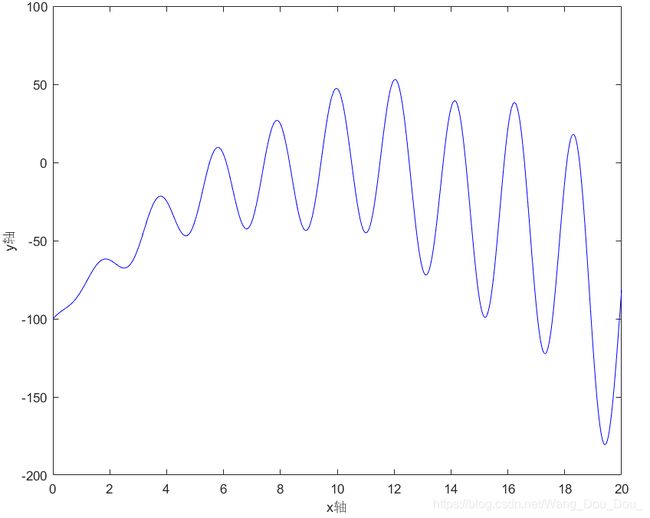
假设我现在要解决 1维 空间的问题(比如:求如下函数的最大值问题)
f ( x ) = − ( x − 10 ) 2 + x × s i n ( x ) c o s ( 2 x ) − 5 x × s i n ( 3 x ) , 其 中 , x ∈ [ 0 , 20 ] f(x)= - (x - 10) ^ 2 + x\times sin(x) cos(2x) - 5 x \times sin(3x) ,其中,x∈[0,20] f(x)=−(x−10)2+x×sin(x)cos(2x)−5x×sin(3x),其中,x∈[0,20]
第一步:初始化
在 D = 1 D=1 D=1 维的空间里,初始化有 N N N 个粒子,这些粒子分别初始化有以下属性 ( 因为这些粒子只能在 x x x轴上运动,所以我称之为一维 ):
①第 i i i 个粒子的位置: x i , i = 1 , 2 , . . . , N x_i,i=1,2,...,N xi,i=1,2,...,N
②第 i i i 个粒子的速度: v i , i = 1 , 2 , . . . , N v_i,i=1,2,...,N vi,i=1,2,...,N
③第 i i i 个粒子所经过的最好的位置: p b e s t i , i = 1 , 2 , . . . , N pbest_i,i=1,2,...,N pbesti,i=1,2,...,N
注:“pbest” 中的 “p” 指得是 “PSO” 中的 “P” → Particle(中文翻译:粒子)
④整个粒子群所经过的最好的位置: g b e s t gbest gbest
注:“gbest” 中的 “g” 指得是 Group .
⑤给所有粒子的 位置 加上限制: x l i m i t i ∈ [ X m i n , X m a x ] , i = 1 , 2 , . . . , N xlimit_i∈[X_{min},X_{max}],i=1,2,...,N xlimiti∈[Xmin,Xmax],i=1,2,...,N。
在上面这个例子里面就是 x l i m i t i ∈ [ 0 , 20 ] , i = 1 , 2 , . . . , N xlimit_i∈[0,20],i=1,2,...,N xlimiti∈[0,20],i=1,2,...,N
⑥给所有粒子的 速度 加上限制: v l i m i t i ∈ [ V m i n , V m a x ] , i = 1 , 2 , . . . , N vlimit_i∈[V_{min},V_{max}],i=1,2,...,N vlimiti∈[Vmin,Vmax],i=1,2,...,N
⑦设置迭代次数 i t e r iter iter。这个例子我假设 i t e r = 50 iter=50 iter=50 。
⑧设在每次迭代过程中,粒子们的自我学习因子 c 1 c_1 c1 。它用来调节 粒子每次移动的步长 受 “自我” 的影响因素大小。
⑨设在每次迭代过程中,粒子们的群体学习因子 c 1 c_1 c1 。它用来调节 粒子每次移动的步长 受 “群体” 的影响因素大小。
⑩设在每次迭代过程中,粒子们的惯性权重为 w w w 。它是一个非负数,用来体现 继承上一刻自己速度的 “能力”。
第二步:计算粒子的适应度
这里的适应度函数就是 f ( x ) = − ( x − 10 ) 2 + x × s i n ( x ) c o s ( 2 x ) − 5 x × s i n ( 3 x ) f(x)= - (x - 10) ^ 2 + x\times sin(x) cos(2x) - 5 x \times sin(3x) f(x)=−(x−10)2+x×sin(x)cos(2x)−5x×sin(3x)
将第 i i i 个粒子当前的位置 x i x_i xi 带入即可得到 该粒子当前的适应度 f ( x i ) f(x_i) f(xi) 。
第三步:更新个体极值与全局最优解
更新 第 i i i 个粒子的个体最佳适应度 f p b e s t ( x i ) f_{pbest}(x_i) fpbest(xi) 和 群体整体的最佳适应度 f g b e s t f_{gbest} fgbest。这两个不仅可以用来画后面的 收敛图,还可以用到 第五步中的方案② 。
再根据 f p b e s t ( x i ) f_{pbest}(x_i) fpbest(xi) 更新 粒子的最佳位置 p b e s t i , i = 1 , 2 , . . . , N pbest_i,i=1,2,...,N pbesti,i=1,2,...,N。
再从这些 最佳位置 p b e s t i pbest_i pbesti 中找到一个群体的最佳位置 g b e s t gbest gbest ,叫做 本次迭代 的全局最佳位置。
第四步:更新个体的速度和位置
更新公式如下: v i = v i × w + c 1 × r a n d ( ) × ( p b e s t i − x i ) + c 2 × r a n d ( ) × ( g b e s t − x i ) v_i = v_i \times w + c_1 \times rand() \times ( pbest_i - x_i) + c_2 \times rand() \times (gbest - x_i) vi=vi×w+c1×rand()×(pbesti−xi)+c2×rand()×(gbest−xi) x i = x i + v i x_i=x_i+v_i xi=xi+vi 说明:①rand() 是 matlab 里面的一个产生 [0,1]之间的随机数函数 。
②若在迭代过程中,第 i i i 个粒子的位置 x i x_i xi 超过了边界 [ X m i n , X m a x ] [X_{min},X_{max}] [Xmin,Xmax] ,则该粒子的 x i x_i xi 被调节为 X m i n X_{min} Xmin 或 X m a x X_{max} Xmax。(看它是超过了下限还是上限)。同理,对于 v i v_i vi 也是这样处理。
第五步:设置终止条件
终止条件一般有这两种方案:
①达到设定迭代次数。
②某一指标与理想目标的差值满足某一最小界限。(可以理解为精度达到某一要求)
若未达到终止条件,则转到第二步。对于这个样例,我采用的是 “终止方案①”。
六、matlab代码实现
clc;clear;close all;
f= @(x) - (x - 10) .^ 2 + x .* sin(x) .* cos(2 * x) - 5 * x .* sin(3 * x) ; % 适应度函数表达式(求这个函数的最大值)
figure(1);
fplot(f, [0 20], 'b-'); % 画出初始图像
d = 1; % 空间维数(该例子是1维)
N = 15; % 初始种群个数
x_limit = [0, 20]; % 设置位置限制
v_limit = [-1, 1]; % 设置速度限制
x = x_limit(1) + (x_limit(2) - x_limit(1)) * rand(N, d); %初始每个粒子的位置
v = rand(N, d); % 初始每个粒子的速度
pbest = x; % 初始化每个个体的历史最佳位置
gbest = zeros(1, d); % 初始化种群的历史最佳位置
fp_best = zeros(N, 1); % 初始化每个个体的历史最佳适应度 为 0
fg_best = -inf; % 初始化种群历史最佳适应度 为 负无穷
iter = 50; % 最大迭代次数
w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.2; % 群体学习因子
hold on;
plot(x, f(x), 'ro');
title('初始状态图');
record = zeros(iter, 1); % 记录器(用于记录 fg_best 的变化过程)
figure(2);
i = 1;
while i <= iter
fx = f(x) ; % 计算个体当前适应度
for j = 1:N
if fp_best(j) < fx(j)
fp_best(j) = fx(j); % 更新个体历史最佳适应度
pbest(j) = x(j); % 更新个体历史最佳位置
end
end
if fg_best < max(fp_best)
[fg_best,ind_max] = max(fp_best); % 更新群体历史最佳适应度
gbest = pbest(ind_max); % 更新群体历史最佳位置,其中 ind_max 是最大值所在的下标
% 注:将上面的两个式子换成下面两个是不可以的
% [gbest, ind_max] = max(pbest); % 更新群体历史最佳位置,其中 ind_max 是最大值所在的下标
% fg_best = fp_best(ind_max); % 更新群体历史最佳适应度
end
v = v * w + c1 * rand() * (pbest - x) + c2 * rand() * (repmat(gbest, N, 1) - x); % 速度更新
% 注: repmat(A,r1,r2):可将矩阵 扩充 为每个单位为A的r1*r2的矩阵
% 边界速度处理
v(v > v_limit(2)) = v_limit(2);
v(v < v_limit(1)) = v_limit(1);
x = x + v;% 位置更新
% 边界位置处理
x(x > x_limit(2)) = x_limit(2);
x(x < x_limit(1)) = x_limit(1);
record(i) = fg_best;%最大值记录
% 画动态展示图
zuo_x = 0 : 0.01 : 20;
plot(zuo_x, f(zuo_x), 'b-', x, f(x), 'ro');
title('状态位置变化')
pause(0.1)
i = i + 1;
% if mod(i,10) == 0 % 显示进度
% i
% end
end
figure(3);
plot(record);
title('收敛过程');
zuo_x = 0 : 0.01 : 20;
figure(4);
plot(zuo_x, f(zuo_x), 'b-', x, f(x), 'ro');
title('最终状态图')
disp(['最佳适应度:',num2str(fg_best)]);
disp(['最佳粒子的位置x:',num2str(gbest)]);
七、运行结果
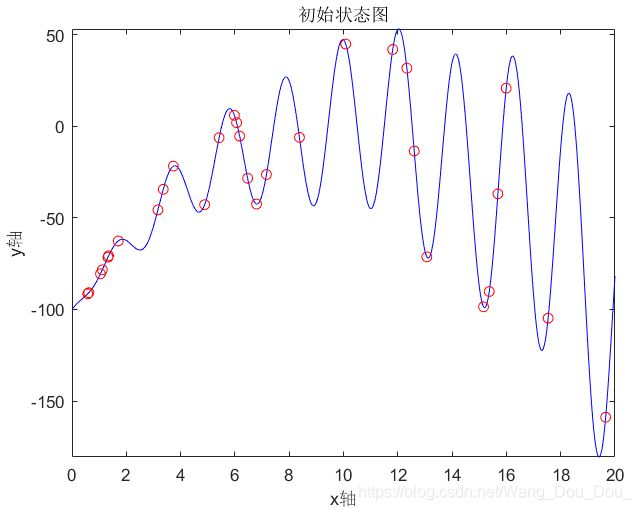
1、各粒子的初始状态位置
2、各粒子的状态位置变化图
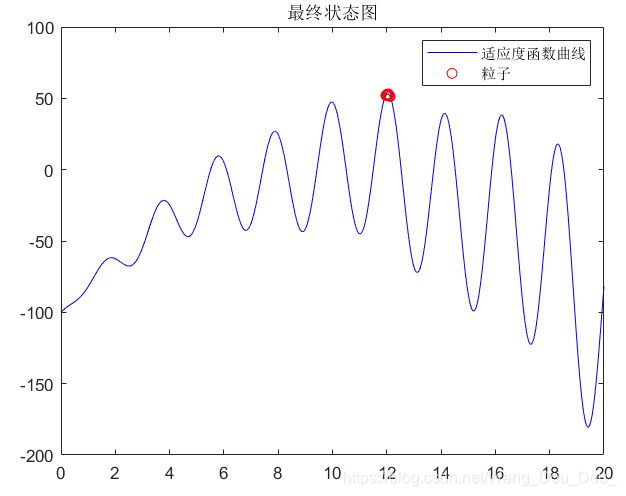
3、各粒子的最终收敛位置
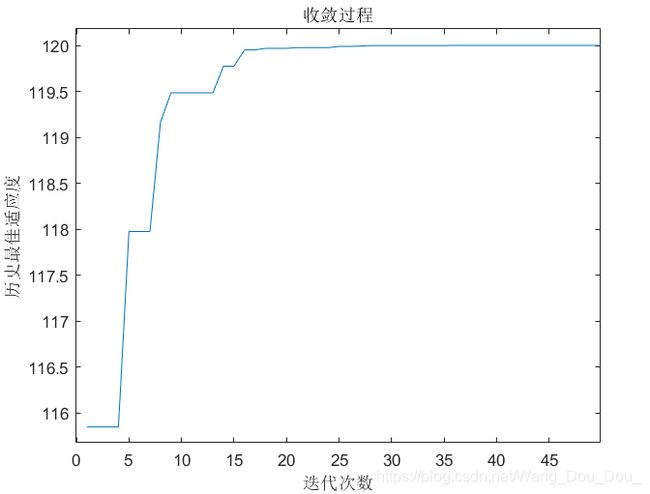
4、收敛过程
注:x 轴代表的是迭代次数,y 轴代表的是 群体的历史最佳适应度 f g b e s t f_{gbest} fgbest 。
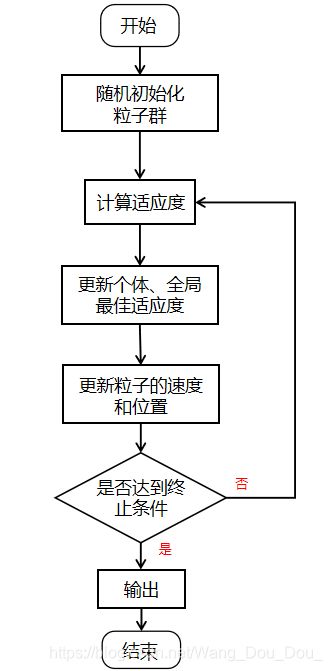
七、粒子群优化算法的使用流程图
八、粒子群优化算法的特点:
(1)它是一类不确定算法。不确定性体现了自然界生物的生物机制,并且 在求解 某些特定问题 方面优于 确定性算法 。
(2)是一类 概率型 的全局优化算法。非确定算法的优点在于算法能有更多机会求解全局最优解。
(3)不依赖于优化问题本身的严格数学性质。
(4)是一种基于多个智能体的 仿生优化算法 。粒子群算法中的各个智能体之间通过 相互协作 来更好的适应环境,表现出与环境交互的能力。
(5)具有自组织性、进化性和记忆功能,所有粒子都保存有最优解的相关 属性 。
(6)都具有稳健性。稳健性是指在不同条件和环境下算法的实用性和有效性,但是现在 粒子群算法的数学理论基础还不够牢固 ,算法的收敛性还需要讨论。
九、拓展知识
上面个例子是针对于 1维 的情况,但是在实际生活中,我们往往是要解决多维的问题。
虽然维度 D D D 增加了,但 算法的核心思想还是没有变 。
知识代码要做相应的变化。下面就以 2维 的例子大致讲一下。(主要是代码变了点)
假设我现在要解决 2维 空间的问题(比如:求如下函数的最大值问题)
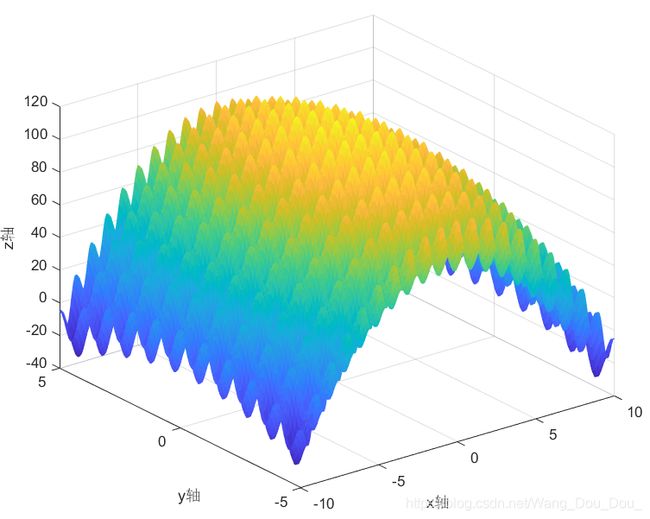
f ( x , y ) = − x 2 − y 2 + 10 × c o s ( 2 π x ) + 10 ∗ c o s ( 2 π y ) + 100 , 其 中 , x ∈ [ − 10 , 10 ] , y ∈ [ − 5 , 5 ] f(x,y) = - x^2 - y^2 + 10 \times cos(2 \pi x) + 10*cos(2 \pi y) + 100,其中,x∈[-10,10] ,y∈[-5,5] f(x,y)=−x2−y2+10×cos(2πx)+10∗cos(2πy)+100,其中,x∈[−10,10],y∈[−5,5]
该函数x新建在 f_xy.m 文件里面
function z = f_xy(x, y)
% 适应度函数
z = - x.^2 - y.^2 + 10*cos(2*pi*x) + 10*cos(2*pi*y) + 100;
end
% 主调用函数
clc;clear;close all;
[ZuoBiao_x, ZuoBiao_y] = meshgrid(-10:0.1:10,-5:0.1:5); % 产生二维坐标
ZuoBiao_z = f_xy(ZuoBiao_x, ZuoBiao_y);
figure(1);
s = mesh(ZuoBiao_x, ZuoBiao_y, ZuoBiao_z); % 画网格曲面图
s.FaceColor = 'flat'; % 修改网格图的属性
% 初始化种群
N = 100; % 初始种群个数
D = 2; % 空间维数
iter = 50; % 迭代次数
x_limit = [-10, 10; -5, 5]; % 位置限制
v_limit = [ -2, 2; -1, 1]; % 速度限制
x = zeros(N, D);
for i = 1:D
x(:,i) = x_limit(i, 1) + (x_limit(i, 2) - x_limit(i, 1)) * rand(N, 1);%初始种群的位置
end
v(:,1) = rands(N, 1) * 1; % 初始种群x方向的速度
v(:,2) = rands(N, 1) * 2; % 初始种群y方向的速度
p_best = x; % (初始化)每个个体的历史最佳位置
f_best = zeros(1, D); % (初始化)种群的历史最佳位置
fp_best = zeros(N, 1) - inf; % (初始化)每个个体的历史最佳适应度为负无穷
fg_best = -inf; % (初始化)种群历史最佳适应度为负无穷
w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子
figure(2);
s = mesh(ZuoBiao_x, ZuoBiao_y, ZuoBiao_z); % 画网格曲面图
s.FaceColor = 'flat'; % 修改网格图的属性
hold on;
plot3(x(:,1), x(:,2),f_xy(x(:,1), x(:,2)), 'ro');
title('初始状态图');
figure(3);
i = 1;
record = zeros(iter, 1); % 记录器
while i <= iter
fx = f_xy(x(:,1), x(:,2)); % 个体当前适应度
for j = 1:N
if fp_best(j) < fx(j) % 记录最大值
fp_best(j) = fx(j); % 更新个体历史最佳适应度
p_best(j,:) = x(j,:); % 更新个体历史最佳位置
end
end
if fg_best < max(fp_best)
[fg_best, ind_max] = max(fp_best); % 更新群体历史最佳适应度
f_best = p_best(ind_max, :); % 更新群体历史最佳位置
end
v = v * w + c1 * rand() * (p_best - x) + c2 * rand() * (repmat(f_best, N, 1) - x); % 速度更新
% 速度处理
for t=1:N
for k=1:D
if v(t,k) > v_limit(k,2) % 超速处理
v(t,k) = v_limit(k,2);
elseif v(t,k) < v_limit(k,1) % 慢速处理
v(t,k) = v_limit(k,1);
end
end
end
x = x + v; % 位置更新
% 边界处理
for t=1:N
for k=1:D
if x(t,k) > x_limit(k,2) % 超过边界上限
x(t,k) = x_limit(k,2);
elseif x(t,k) < x_limit(k,1) % 超过边界下限
x(t,k) = x_limit(k,1);
end
end
end
record(i) = fg_best; % 最大值记录
i = i + 1;
if mod(i,10) == 0
i % 收敛进度输出
end
pause(0.1)
end
figure(4)
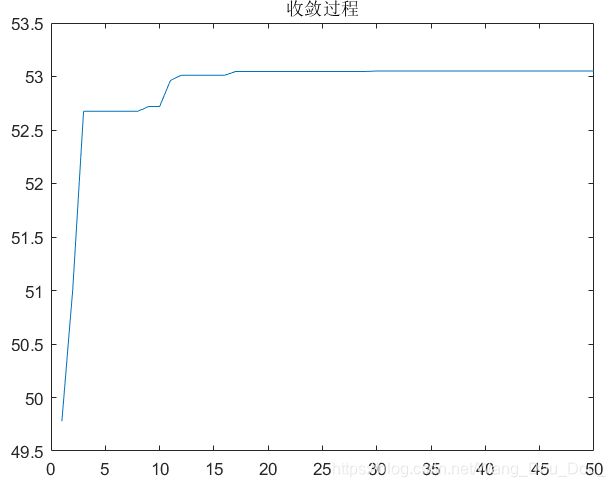
plot(record);
title('收敛过程');
% 画最终状态图
figure(5);
[ZuoBiao_x, ZuoBiao_y] = meshgrid(-10:0.1:10,-5:0.1:5); % 产生二维坐标
s = mesh(ZuoBiao_x, ZuoBiao_y, ZuoBiao_z); % 画网格曲面图
s.FaceColor = 'flat'; % 修改网格图的属性
hold on;
scatter3(x(:,1), x(:,2), f_xy(x(:,1), x(:,2)), 'ro');
title('最终状态图')
disp(['最大值:',num2str(fg_best)]);
disp(['变量取值:',num2str(f_best)]);
% 下面一段用来输出 粒子群最佳适应度的排行榜
[socre,ind] = sort(fp_best, 'descend') % 降序排序
DaAn = zeros(3,2);
for i=1:N
row = ind(i);
DaAn(i,:) = p_best(row,:);
end
运行结果:
十、总结:
本文细分目录,从头到尾 大致 讲解了PSO的定义、原理、实现、配合样例和相关拓展。主要内容如下:
①粒子群优化算法是什么?
②粒子群优化算法(PSO)是什么?
③粒子群优化算法有什么用?
④粒子群优化算法的适用范围?
⑤算法简介(有助于理解)
⑥算法的实现流程
⑦matlab代码实现
⑧粒子群优化算法的使用流程图
⑨粒子群优化算法的特点
⑩拓展知识(1维→多维)
最后,我没有 非常深入 地阐述其原理,只阐述了有什么用、怎么用。如要了解详细的原理,可以看看文章最后的 参考附录 。
十一、参考附录:
[1] 《粒子群优化算法(PSO)》
阅读这篇文章可以知道 PSO 的 研究背景、来源和主要应用
链接: https://blog.csdn.net/weixin_40679412/article/details/80571854.
[2] 《粒子群优化算法 很好的博客》
这篇文章的最后讲解了c1、c2的深刻含义。
链接: https://blog.csdn.net/zqx951102/article/details/89927955.
数学建模系列文章——总结篇:《数模美一国一退役选手的经验分享[2021纪念版]》.
⭐️ ⭐️