LDA隐狄利克雷分配
LDA隐狄利克雷分配
因为组会汇报系统学习了一下LDA,顺便将自己的讲稿记录在博客上。
1. 主题模型
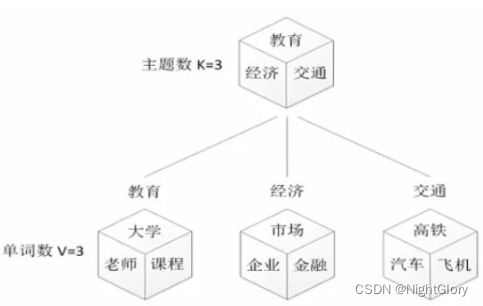
主题模型是一种能够在大量文档中挖掘抽象主题的统计模型。它能够将复杂的非结构化文档中的高维词汇空间映射到文档-主题-单词的低维空间,从而获取到文档的主题分布。
一篇文章的每个词都是以一定概率选择了某个主题,并从这个主题中以一定概率选择某个词语而组成的。
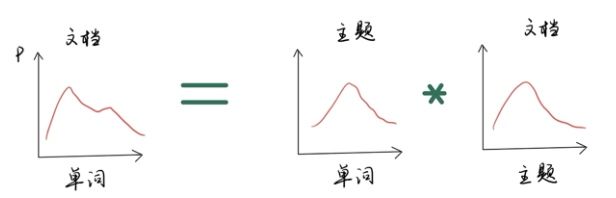
具体而言,一个文档的单词分布可以转换成文档-主题分布和主题-单词分布的乘积,即:
P ( 单 词 ∣ 文 档 ) = P ( 单 词 ∣ 主 题 ) × P ( 主 题 ∣ 文 档 ) P(单词|文档)=P(单词|主题)\times P(主题|文档) P(单词∣文档)=P(单词∣主题)×P(主题∣文档)
上式可以从贝叶斯的角度推导出来,也可以从条件分布的定义推导出来。该公式被称为条件概率的链式法则。
对于上面的核心公式,我们首先要明确我们的任务是获取特定文档的主题,这也是主题模型的目标,我们通过假定文档的主题分布,将单词 W W W和文档 D D D联系起来,原始文档的单词分布 P ( W ∣ D ) P(W|D) P(W∣D)就是我们的训练数据,用来学习两个分布 P ( W ∣ T ) P(W|T) P(W∣T)和 P ( T ∣ D ) P(T|D) P(T∣D)。学习的过程就是不断拟合的过程,最终,我们将学到的分布 P ( T ∣ D ) P(T|D) P(T∣D)作为我们模型的输出。
通过上面的描述,我们可以知道主题模型的训练其实是非常消耗时间的,因为要从一个分布中拟合另外两个分布。同时对训练的技巧提出了要求。
以词袋模型方向为例,我们了解一下主题模型的发展路径。
所谓词袋模型是指词与词之间没有任何关联,仅统计词汇的数理统计信息。
词袋模型方向的主题模型大体经历了如图所示的发展路径。从最初的Unigrams模型,直接统计文档与单词数量的关联,到混合Unigrams模型中引入了中间层主题层,再到PLSA(概率潜在语义分析)假设文档包含多个主题,且主题间符合某种分布,然后到LDA在PLSA基础上增加了贝叶斯框架。LDA本质上是PLSA的贝叶斯版本。
L D A = P L S A + 先 验 LDA=PLSA+先验 LDA=PLSA+先验
LDA是一种混合概率模型,它通过最大化词语共现概率寻找词语聚类,利用狄利克雷分布刻画文档生 成过程,并限定文档主题数量,避免PLSA方法过拟合以及参数过多的问题。
LDA也是一个典型的词袋模型。
那么我们就从贝叶斯的角度来看看LDA的具体内容吧。
2. 基础知识
要理解LDA模型,主要是需要了解下面的几个概念:
- 一个函数:Gamma函数
- 四个分布:二项分布、多项分布、beta分布、Dirichlet分布
- 一个概念和一个理念:共轭先验和贝叶斯框架
- 两个模型:PLSA、LDA
- 一个采样:Gibbs采样
我们首先从贝叶斯框架聊起。贝叶斯公式在统计学上的解释是这样的:
后 验 概 率 ∝ 似 然 函 数 × 先 验 概 率 后验概率 \propto 似然函数\times 先验概率 后验概率∝似然函数×先验概率
其中似然函数也就是样本信息。
其次我们还需要知道的一个概念是共轭先验:如果后验概率分布与先验概率分布属于同一类型(参数不必相同),则称先验概率和后验概率为共轭分布,先验概率分布被称为共轭先验。后面会提到几个共轭分布。
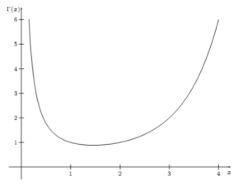
在了解四个分布之前,我们先了解一下Gamma函数。其实Gamma函数是阶乘函数在实数上的推广。即对整数而言:
Γ ( n ) = ( n − 1 ) ! \Gamma(n)=(n-1)! Γ(n)=(n−1)!
对于实数而言:
Γ ( x ) = ∫ 0 ∞ t x − 1 e − t d t \Gamma(x)=\int_{0}^{\infty} t^{x-1} e^{-t} \mathrm{~d} t Γ(x)=∫0∞tx−1e−t dt
二项分布是多次试验的伯努利分布,其概率密度函数为:
P { X = k } = ( n k ) p k ( 1 − p ) n − k P\{X=k\}=\left(\begin{array}{c} n \\ k \end{array}\right) p^{k}(1-p)^{n-k} P{X=k}=(nk)pk(1−p)n−k
多项分布是二项分布拓展到多维的情况。
概率密度函数:
P ( X 1 = x 1 , X 2 = x 2 , … , X k = x k ) = n ! x 1 ! x 2 ! ⋯ x k ! p 1 x 1 p 2 x 2 ⋯ p k x k P\left(X_{1}=x_{1}, X_{2}=x_{2}, \ldots, X_{k}=x_{k}\right)=\frac{n !}{x_{1} ! x_{2} ! \cdots x_{k} !} p_{1}^{x_{1}} p_{2}^{x_{2}} \cdots p_{k}^{x_{k}} P(X1=x1,X2=x2,…,Xk=xk)=x1!x2!⋯xk!n!p1x1p2x2⋯pkxk
Bata分布是二项分布的共轭先验分布。也是从离散型到连续型的拓展。
给定参数 a > 0 a>0 a>0 和 b > 0 b>0 b>0 ,取值范围为 [ 0 , 1 ] [0,1] [0,1] 的随机变量 x x x 的概率密度函数:
f ( x ; α , β ) = 1 B ( α , β ) x α − 1 ( 1 − x ) β − 1 f(x ; \alpha, \beta)=\frac{1}{B(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1} f(x;α,β)=B(α,β)1xα−1(1−x)β−1
其中
B ( α , β ) = Γ ( α ) Γ ( β ) Γ ( α + β ) B(\alpha, \beta)=\frac{\Gamma(\alpha) \Gamma(\beta)}{\Gamma(\alpha+\beta)} B(α,β)=Γ(α+β)Γ(α)Γ(β)
最后,Dirichlet分布是Beta分布在高维度上的推广。将Beta分布的一个变量 x x x拓展为向量,两个参数拓展为多个参数。其概率密度函数如下:
Dir ( X ∣ α ) = f ( x 1 , ⋯ , x k ; α 1 , ⋯ , α k ) = 1 B ( α ) ∏ i = 1 d X i α i − 1 \operatorname{Dir}(\boldsymbol{X} \mid \boldsymbol{\alpha})=f\left(x_{1}, \cdots, x_{k} ; \alpha_{1}, \cdots, \alpha_{k}\right)=\frac{1}{\mathrm{~B}(\boldsymbol{\alpha})} \prod_{i=1}^{d} X_{i}^{\alpha_{i}-1} Dir(X∣α)=f(x1,⋯,xk;α1,⋯,αk)= B(α)1i=1∏dXiαi−1
其中
B ( α ) = ∏ i = 1 d Γ ( α i ) Γ ( α 0 ) , α 0 = ∑ i = 1 d α i , d ≥ 3 \mathrm{B}(\boldsymbol{\alpha})=\frac{\prod_{i=1}^{d} \Gamma\left(\alpha_{i}\right)}{\Gamma\left(\alpha_{0}\right)}, \quad \alpha_{0}=\sum_{i=1}^{d} \alpha_{i}, \quad d \geq 3 B(α)=Γ(α0)∏i=1dΓ(αi),α0=i=1∑dαi,d≥3
我们以三维为例,通过观察这里的热力图,我们可以发现该分布可以通过对参数的调整来设定范围和位置。以此达到我们需要的分布。
以上四个概率分布之间的关系是:
3. LDA模型
假设「文本-主题」和「主题-单词」的概率分布符合上述分析的最高阶的Dirichlet分布。同时通过样本获取对参数的先验估计,将模型导向更加合理的参数。
以贝叶斯的视角即:
参 数 的 后 验 概 率 ∝ 似 然 函 数 × 先 验 概 率 参数的后验概率 \propto 似然函数\times 先验概率 参数的后验概率∝似然函数×先验概率
先验分布的导入使得LDA能够更好地应对主题模型学习过程的过拟合现象,因为Dirichlet先验暗含了一个假设:样本分布往往是稀疏的。
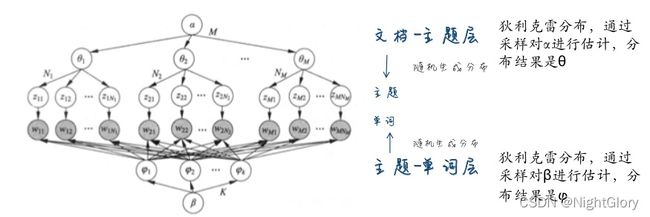
LDA是概率图模型,其特点是以狄利克雷分布为多项分布的先验分布,学习就是给定文本集合,通过后验概率分布的估计,推断模型的所有参数,利用LDA进行话题分析,即使对给定的文本集合,学习到每个文本的话题分布,以及每个话题的单词分布。
如图,通过对两个先验分布的估计,逐渐拟合到合适的参数,使得两个分布的组合能够很好的解释我们所能从样本中观察到的单词统计数据,即这里的观测变量。
对比两个算法:
- LDA避免了刻板印象对主题分布的影响,防止过拟合。而刻板印象通常意味着局部最优解。
- PLSA与LDA的本质区别在于它们去估计未知参数所采用的思想不同,前者采用的是频率派的思想(条件概率分布),后者用的是贝叶斯派的思想。
- 狄利克雷分布的超参数 α α α 和 β β β 通常也是事先给定的。在没有其他先验知识的情况下,可以假设向量 α α α 和 β β β 的所有分量均为 1 1 1。 这时的文本的话题分布 θ m \theta_m θm是对称的,话题的单词分布 φ k \varphi_k φk也是对称的。
性能对比上:
- 文本聚类:两者差不多
- 文档分类:LDA略好
- LDA主题比PLSA主题更稀疏,主题稀疏性提高了主题的可读性
要是你恰好数学能力优秀,上面的算法可以用一个式子表示:
p ( w , z , θ , φ ∣ α , β ) = ∏ k = 1 K p ( φ k ∣ β ) ∏ m = 1 M p ( θ m ∣ α ) ∏ n = 1 N m p ( z m n ∣ θ m ) p ( w m n ∣ z m n , φ ) p(\mathbf{w}, \mathbf{z}, \theta, \varphi \mid \alpha, \beta)=\prod_{k=1}^{K} p\left(\varphi_{k} \mid \beta\right) \prod_{m=1}^{M} p\left(\theta_{m} \mid \alpha\right) \prod_{n=1}^{N_{m}} p\left(z_{m n} \mid \theta_{m}\right) p\left(w_{m n} \mid z_{m n}, \varphi\right) p(w,z,θ,φ∣α,β)=k=1∏Kp(φk∣β)m=1∏Mp(θm∣α)n=1∏Nmp(zmn∣θm)p(wmn∣zmn,φ)
具体参考《统计学习方法2》
LDA的展开图模型如下:
4. 吉布斯采样
LDA模型的学习通常采用收缩的吉布斯抽样 (collapsed Gibbs sampling)方法,基本想法是,通过对隐变量 θ \theta θ和 φ \varphi φ 积分, 得到边缘概率分布 p ( w , z ∣ α , β ) p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta) p(w,z∣α,β) (也是联合分布),其中变量 w \mathbf{w} w 是可观测的,变量 z \mathbf{z} z 是不可观测的;对后验概率分布 p ( z ∣ w , α , β ) p(\mathbf{z}| \mathbf{w}, \alpha, \beta) p(z∣w,α,β) 进行吉布斯抽样,得到分布 p ( z ∣ w , α , β ) p(\mathbf{z}| \mathbf{w}, \alpha, \beta) p(z∣w,α,β) 的样本集合;再利用这个样本集合对参数 θ \theta θ和 φ \varphi φ 进行估计,最终得到 LDA 模型 p ( w , z , θ , φ ∣ α , β ) p(\mathbf{w}, \mathbf{z}, \theta, \varphi \mid \alpha, \beta) p(w,z,θ,φ∣α,β) 的所有参数估计。
数学小课堂开始啦:根据刚才的分析,条件概率分布可分解为:
p ( z ∣ w , α , β ) = p ( w , z ∣ α , β ) p ( w ∣ α , β ) ∝ p ( w , z ∣ α , β ) p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta)=\frac{p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta)}{p(\mathbf{w} \mid \alpha, \beta)} \propto p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta) p(z∣w,α,β)=p(w∣α,β)p(w,z∣α,β)∝p(w,z∣α,β)
联合分布的分解:
p ( w , z ∣ α , β ) = p ( w ∣ z , α , β ) p ( z ∣ α , β ) = p ( w ∣ z , β ) p ( z ∣ α ) \begin{array}{c} p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta)=p(\mathbf{w} \mid \mathbf{z}, \alpha, \beta) p(\mathbf{z} \mid \alpha, \beta) \\ =p(\mathbf{w} \mid \mathbf{z}, \beta) p(\mathbf{z} \mid \alpha) \end{array} p(w,z∣α,β)=p(w∣z,α,β)p(z∣α,β)=p(w∣z,β)p(z∣α)
左边为:
p ( w ∣ z , β ) = ∫ p ( w ∣ z , φ ) p ( φ ∣ β ) d φ = ∫ ∏ k = 1 K 1 B ( β ) ∏ v = 1 V φ k v n k v + β v − 1 d φ = ∏ k = 1 K 1 B ( β ) ∫ ∏ v = 1 V φ k v n k v + β v − 1 d φ = ∏ k = 1 K B ( n k + β ) B ( β ) \begin{aligned} p(\mathbf{w} \mid \mathbf{z}, \beta) &=\int p(\mathbf{w} \mid \mathbf{z}, \varphi) p(\varphi \mid \beta) \mathrm{d} \varphi \\ &=\int \prod_{k=1}^{K} \frac{1}{\mathrm{~B}(\beta)} \prod_{v=1}^{V} \varphi_{k v}^{n_{k v}+\beta_{v}-1} \mathrm{~d} \varphi \\ &=\prod_{k=1}^{K} \frac{1}{\mathrm{~B}(\beta)} \int \prod_{v=1}^{V} \varphi_{k v}^{n_{k v}+\beta_{v}-1} \mathrm{~d} \varphi \\ &=\prod_{k=1}^{K} \frac{\mathrm{B}\left(n_{k}+\beta\right)}{\mathrm{B}(\beta)} \end{aligned} p(w∣z,β)=∫p(w∣z,φ)p(φ∣β)dφ=∫k=1∏K B(β)1v=1∏Vφkvnkv+βv−1 dφ=k=1∏K B(β)1∫v=1∏Vφkvnkv+βv−1 dφ=k=1∏KB(β)B(nk+β)
其中
p ( w ∣ z , φ ) = ∏ k = 1 K ∏ v = 1 V φ k v n k v p(\mathbf{w} \mid \mathbf{z}, \varphi)=\prod_{k=1}^{K} \prod_{v=1}^{V} \varphi_{k v}^{n_{k v}} p(w∣z,φ)=k=1∏Kv=1∏Vφkvnkv
右边为:
p ( z ∣ α ) = ∫ p ( z ∣ θ ) p ( θ ∣ α ) d θ = ∫ ∏ m = 1 M 1 B ( α ) ∏ k = 1 K θ m k n m k + α k − 1 d θ = ∏ m = 1 M 1 B ( α ) ∫ ∏ k = 1 K θ m k n m k + α k − 1 d θ = ∏ m = 1 M B ( n m + α ) B ( α ) \begin{aligned} p(\mathbf{z} \mid \alpha) &=\int p(\mathbf{z} \mid \theta) p(\theta \mid \alpha) \mathrm{d} \theta \\ &=\int \prod_{m=1}^{M} \frac{1}{\mathrm{~B}(\alpha)} \prod_{k=1}^{K} \theta_{m k}^{n_{m k}+\alpha_{k}-1} \mathrm{~d} \theta \\ &=\prod_{m=1}^{M} \frac{1}{\mathrm{~B}(\alpha)} \int \prod_{k=1}^{K} \theta_{m k}^{n_{m k}+\alpha_{k}-1} \mathrm{~d} \theta \\ &=\prod_{m=1}^{M} \frac{\mathrm{B}\left(n_{m}+\alpha\right)}{\mathrm{B}(\alpha)} \end{aligned} p(z∣α)=∫p(z∣θ)p(θ∣α)dθ=∫m=1∏M B(α)1k=1∏Kθmknmk+αk−1 dθ=m=1∏M B(α)1∫k=1∏Kθmknmk+αk−1 dθ=m=1∏MB(α)B(nm+α)
其中
p ( z ∣ θ ) = ∏ m = 1 M ∏ k = 1 K θ m k n m k p(\mathbf{z} \mid \theta)=\prod_{m=1}^{M} \prod_{k=1}^{K} \theta_{m k}^{n_{m k}} p(z∣θ)=m=1∏Mk=1∏Kθmknmk
再将两个式子合并到一起:
p ( z , w ∣ α , β ) = ∏ k = 1 K B ( n k + β ) B ( β ) ⋅ ∏ m = 1 M B ( n m + α ) B ( α ) p(\mathbf{z}, \mathbf{w} \mid \alpha, \beta)=\prod_{k=1}^{K} \frac{\mathrm{B}\left(n_{k}+\beta\right)}{\mathrm{B}(\beta)} \cdot \prod_{m=1}^{M} \frac{\mathrm{B}\left(n_{m}+\alpha\right)}{\mathrm{B}(\alpha)} p(z,w∣α,β)=k=1∏KB(β)B(nk+β)⋅m=1∏MB(α)B(nm+α)
结合
p ( z ∣ w , α , β ) = p ( w , z ∣ α , β ) p ( w ∣ α , β ) ∝ p ( w , z ∣ α , β ) p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta)=\frac{p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta)}{p(\mathbf{w} \mid \alpha, \beta)} \propto p(\mathbf{w}, \mathbf{z} \mid \alpha, \beta) p(z∣w,α,β)=p(w∣α,β)p(w,z∣α,β)∝p(w,z∣α,β)
最终可得:
p ( z ∣ w , α , β ) ∝ ∏ k = 1 K B ( n k + β ) B ( β ) ⋅ ∏ m = 1 M B ( n m + α ) B ( α ) p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta) \propto \prod_{k=1}^{K} \frac{\mathrm{B}\left(n_{k}+\beta\right)}{\mathrm{B}(\beta)} \cdot \prod_{m=1}^{M} \frac{\mathrm{B}\left(n_{m}+\alpha\right)}{\mathrm{B}(\alpha)} p(z∣w,α,β)∝k=1∏KB(β)B(nk+β)⋅m=1∏MB(α)B(nm+α)
接下来,我们用满条件分布来从采样的样本中估计相关参数。分布 p ( z ∣ w , α , β ) p(\mathbf{z}| \mathbf{w}, \alpha, \beta) p(z∣w,α,β)的满条件分布可以写成:
p ( z i ∣ z − i , w , α , β ) = 1 Z z i p ( z ∣ w , α , β ) p\left(z_{i} \mid \mathbf{z}_{-i}, \mathbf{w}, \alpha, \beta\right)=\frac{1}{Z_{z_{i}}} p(\mathbf{z} \mid \mathbf{w}, \alpha, \beta) p(zi∣z−i,w,α,β)=Zzi1p(z∣w,α,β)
结合上面推导的公式
p ( z i ∣ z − i , w , α , β ) ∝ n k v + β v ∑ v = 1 V ( n k v + β v ) ⋅ n m k + α k ∑ k = 1 K ( n m k + α k ) p\left(z_{i} \mid \mathbf{z}_{-i}, \mathbf{w}, \alpha, \beta\right) \propto \frac{n_{k v}+\beta_{v}}{\sum_{v=1}^{V}\left(n_{k v}+\beta_{v}\right)} \cdot \frac{n_{m k}+\alpha_{k}}{\sum_{k=1}^{K}\left(n_{m k}+\alpha_{k}\right)} p(zi∣z−i,w,α,β)∝∑v=1V(nkv+βv)nkv+βv⋅∑k=1K(nmk+αk)nmk+αk
其中第 m m m 个文本的第 n n n 个位置的单词 w i w_i wi是单词集合的第 v v v 个单词,其话题 Z i Z_i Zi 是话题集合的第 k k k 个话题, n k v n_{kv} nkv 表示第 k k k 个话题中第 v v v 个单词的计数,但减去当前单词的计数, n m k n_{mk} nmk 表示第 m m m 个文本中第 k k k 个话题的计数,但减去当前单词的话题的计数。
通过吉布斯抽样得到的分布 p ( z ∣ w , α , β ) p(\mathbf{z}| \mathbf{w}, \alpha, \beta) p(z∣w,α,β)的样本,可以得到变量 z z z 的分配值,也可以估计变量 θ θ θ和 φ \varphi φ。
-
参数 θ = { θ m } θ=\left\{θ_m\right\} θ={θm}的估计:
p ( θ m ∣ z m , α ) = 1 Z θ m ∏ n = 1 N m p ( z m n ∣ θ m ) p ( θ m ∣ α ) = Dir ( θ m ∣ n m + α ) p\left(\theta_{m} \mid \mathbf{z}_{m}, \alpha\right)=\frac{1}{Z_{\theta_{m}}} \prod_{n=1}^{N_{m}} p\left(z_{m n} \mid \theta_{m}\right) p\left(\theta_{m} \mid \alpha\right)=\operatorname{Dir}\left(\theta_{m} \mid n_{m}+\alpha\right) p(θm∣zm,α)=Zθm1n=1∏Nmp(zmn∣θm)p(θm∣α)=Dir(θm∣nm+α)
推导可得:
θ m k = n m k + α k ∑ k = 1 K ( n m k + α k ) \theta_{m k}=\frac{n_{m k}+\alpha_{k}}{\sum_{k=1}^{K}\left(n_{m k}+\alpha_{k}\right)} θmk=∑k=1K(nmk+αk)nmk+αk
这里 n m = { n m 1 , n m 2 , ⋯ , n m K } n_{m}=\left\{n_{m 1}, n_{m 2}, \cdots, n_{m K}\right\} nm={nm1,nm2,⋯,nmK}是第 m m m个文本的话题的计数, Z θ m Z_{\theta_m} Zθm表示分布 p ( θ m , z m ∣ α ) p\left(\theta_{m}, \mathbf{z}_{m} \mid \alpha\right) p(θm,zm∣α)对变量 θ m \theta_m θm的边缘化因子。
-
参数 φ = { φ k } φ=\left\{φ_k\right\} φ={φk} 的估计:
p ( φ k ∣ w , z , β ) = 1 Z φ k ∏ i = 1 I p ( w i ∣ φ k ) p ( φ k ∣ β ) = Dir ( φ k ∣ n k + β ) p\left(\varphi_{k} \mid \mathbf{w}, \mathbf{z}, \beta\right)=\frac{1}{Z_{\varphi_{k}}} \prod_{i=1}^{I} p\left(w_{i} \mid \varphi_{k}\right) p\left(\varphi_{k} \mid \beta\right)=\operatorname{Dir}\left(\varphi_{k} \mid n_{k}+\beta\right) p(φk∣w,z,β)=Zφk1i=1∏Ip(wi∣φk)p(φk∣β)=Dir(φk∣nk+β)
推导可得:
φ k v = n k v + β v ∑ v = 1 V ( n k v + β v ) \varphi_{k v}=\frac{n_{k v}+\beta_{v}}{\sum_{v=1}^{V} \left(n_{k v}+\beta_{v}\right)} φkv=∑v=1V(nkv+βv)nkv+βv
上面推导的 θ \theta θ的估计对应的分布就是文档-主题分布。也就是我们的目标。
总览一下LDA的吉布斯采样算法:
5. LDA等主题模型的应用
- 文本主题分析
- 文本分类/聚类
- 文本生成任务
- 文档降维
文档降维:用得到的文本-话题分布参数表示文档。
缺点:短文本(微博、短评)效果不好。
解决方法:词嵌入/主题嵌入(因为嵌入技术考虑了上下文关系)
这就是另一个大的话题了~