机器学习之线性回归
机器学习之线性回归
- 1 线性回归
-
- 1.1 定义
- 1.2 一元线性回归
- 1.3 多元线性回归
- 1.4 损失函数
- 1.5 欠拟合与过拟合
- 2 代码实现正规方程算法
- 3 代码实现梯度下降算法
- 4 代码实现岭回归算法
前言:主要介绍线性回归的定义,线性回归的分类,损失函数,正规方程、梯度下降、岭回归算法的代码实现。
1 线性回归
1.1 定义
线性回归通过一个或者多个自变量与因变量之间之间进行建模的回归分析。其中特点为一个或多个称为回归系数的模型参数的线性组合。
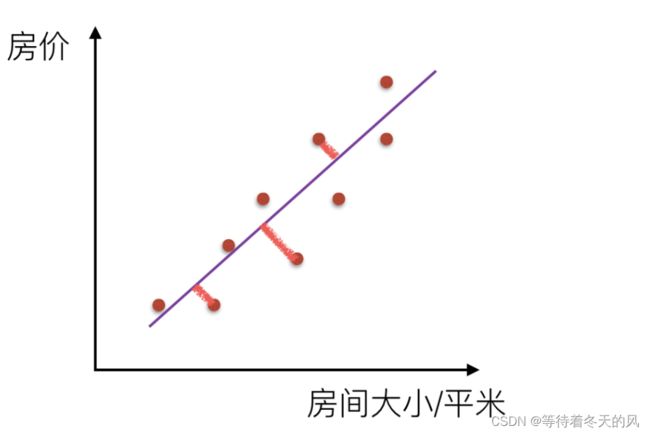
1.2 一元线性回归
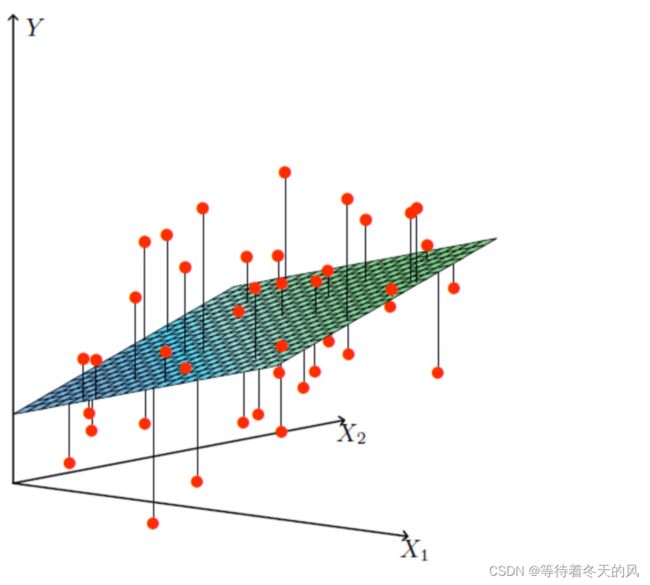
1.3 多元线性回归
- 线性模型中的向量W值,客观的表达了各属性在预测中的重要性,因此线性模型有很好的解释性。对于这种“多特征预测”也就是(多元线性回归),那么线性回归就是在这个基础上得到这些W的值,然后以这些值来建立模型,预测测试数据。简单的来说就是学得一个线性模型以尽可能准确的预测实值输出标记。
1.4 损失函数
- 损失函数是一个贯穿整个机器学习重要的一个概念,大部分机器学习算法都会有误差,我们得通过显性的公式来描述这个误差,并且将这个误差优化到最小值。
- 对于线性回归模型,将模型与数据点之间的距离差之和做为衡量匹配好坏的标准,误差越小,匹配程度越大。我们要找的模型就是需要将f(x)和我们的真实值之间最相似的状态。于是我们就有了误差公式,模型与数据差的平方和最小:

1.5 欠拟合与过拟合
机器学习中的泛化,泛化即是,模型学习到的概念在它处于学习的过程中时模型没有遇见过的样本时候的表现。在机器学习领域中,当我们讨论一个机器学习模型学习和泛化的好坏时,我们通常使用术语:过拟合和欠拟合。我们知道模型训练和测试的时候有两套数据,训练集和测试集。在对训练数据进行拟合时,需要照顾到每个点,而其中有一些噪点,当某个模型过度的学习训练数据中的细节和噪音,以至于模型在新的数据上表现很差,这样的话模型容易复杂,拟合程度较高,造成过拟合。而相反如果值描绘了一部分数据那么模型复杂度过于简单,欠拟合指的是模型在训练和预测时表现都不好的情况,称为欠拟合。
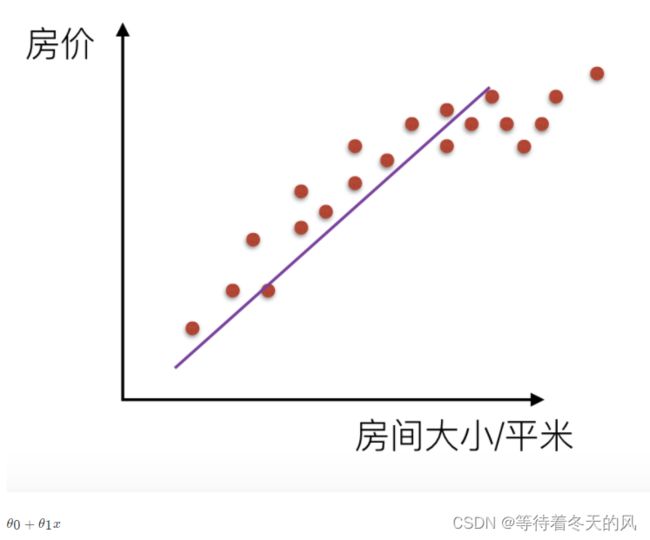
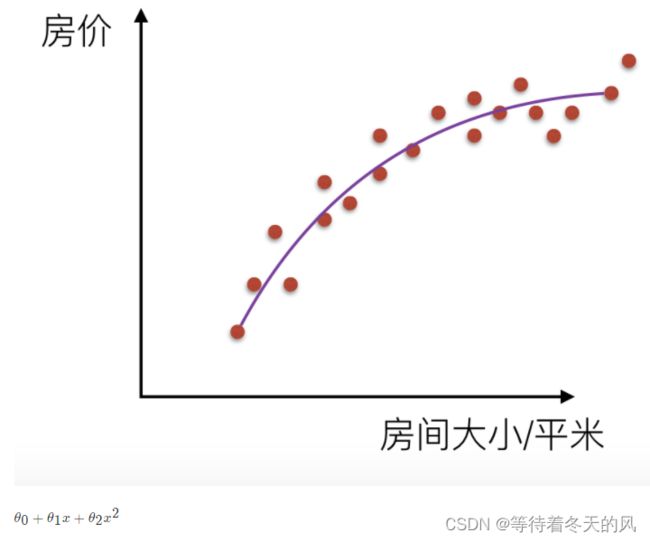

- 解决欠拟合:欠拟合指的是模型在训练和预测时表现都不好的情况,欠拟合通常不被讨论,因为给定一个评估模型表现的指标的情况下,欠拟合很容易被发现。矫正方法是继续学习并且试着更换机器学习算法。
- 解决过拟合:对于过拟合,特征集合数目过多,我们需要做的是尽量不让回归系数数量变多,对拟合(损失函数)加以限制。
2 代码实现正规方程算法
代码如下(以预测波士顿房价为例):
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def mylinner():
"""
线性回归预测房子价格
"""
lb = load_boston()
# x_train, x_test是特征值 y_train, y_test是目标值
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
#特征化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.fit_transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))
# estimator预测
# 正规方程求解方式预测结果
lr = LinearRegression()
lr.fit(x_train, y_train)
print(lr.coef_) #回归系数
#预测测试集的房子价格
y_predict = std_y.inverse_transform(lr.predict(x_test))
for y in y_predict:
print(y[0])
print("正规方程的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_predict))
if __name__ == '__main__':
mylinner()
pass
3 代码实现梯度下降算法
代码如下(以预测波士顿房价为例):
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def mylinner():
"""
线性回归预测房子价格
:return:
"""
lb = load_boston()
# x_train, x_test是特征值 y_train, y_test是目标值
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
#特征化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.fit_transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))
# 梯度下降去进行房价预测
sgd = SGDRegressor()
sgd.fit(x_train, y_train)
print(sgd.coef_)
#预测测试集的房子价格
y_predict = std_y.inverse_transform(sgd.predict(x_test))
for y in y_predict:
print(y)
print("梯度下降的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_predict))
if __name__ == '__main__':
mylinner()
pass
4 代码实现岭回归算法
代码如下(以预测波士顿房价为例):
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
def mylinner():
"""
线性回归预测房子价格
:return:
"""
lb = load_boston()
# x_train, x_test是特征值 y_train, y_test是目标值
x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25)
#特征化
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.fit_transform(x_test)
# 目标值
std_y = StandardScaler()
y_train = std_y.fit_transform(y_train.reshape(-1,1))
y_test = std_y.transform(y_test.reshape(-1,1))
# 岭回归去进行房价预测
rd = Ridge(alpha=1.0)
rd.fit(x_train, y_train)
print(rd.coef_)
# 预测测试集的房子价格
y_predict = std_y.inverse_transform(rd.predict(x_test))
for y in y_predict:
print(y[0])
print("岭回归的均方误差:", mean_squared_error(std_y.inverse_transform(y_test), y_predict))
if __name__ == '__main__':
mylinner()
pass