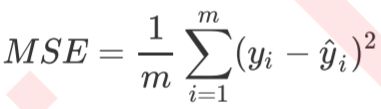数据挖掘：模型评估指标

数据挖掘：模型评估

一般在比赛中，我们会看到对于回归（分类）问题，不同的比赛会有不同的评价指标。我们在训练模型时，不能只记住回归问题用均方误差，而不去在意比赛目标的评价指标，这样我们往往会得到比较差的结果，南辕北辙。

一、为什么会有这么多衡量的指标

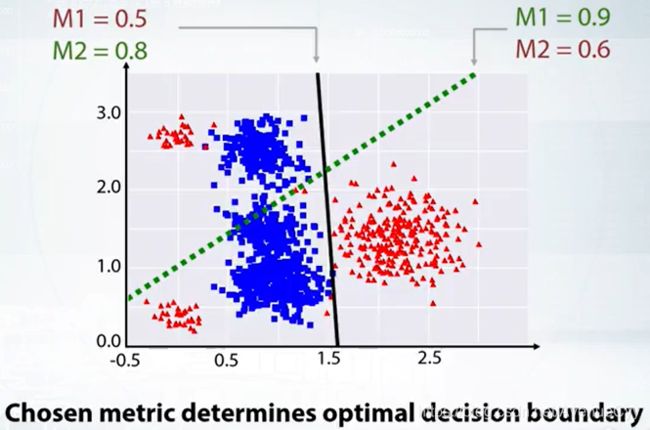
因为具体场景不同，比赛会有不同的偏向。比如，同一个问题，M1和M2分类的准确率不一样，这时，就需要看具体的要求，如果侧重M1多一些，那么在优化时，就应该对M1进行侧重优化。

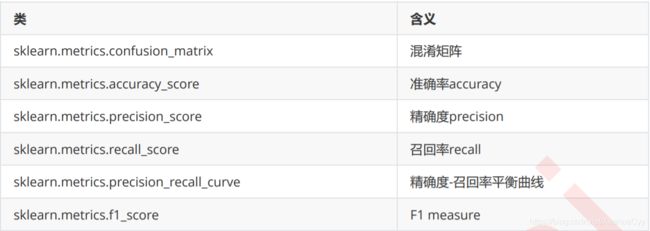
常见的一些评价指标。

这里贴出网上写的比较好的模型评估的文章，由于本人的知识量有限，无法做出较好的总结，因此先参考别人的。等以后对这块更加熟悉后，再做补充。
机器学习模型的评价指标和方法
机器学习模型评价(Evaluating Machine Learning Models)-主要概念与陷阱
机器学习模型相关评价指标最全总结
模型评估常用指标
另外，本篇文章也是来自菜菜机器学习。

二、回归问题评估指标

回归类与分类型算法的模型评估其实是相似的法则——找真实标签和预测值的差异。回归类算法中，我们有两种不同的角度来看待回归的效果：
第一，我们是否预测到了正确的数值。
第二，我们是否拟合到了足够的信息。
这两种角度，分别对应着不同的模型评估指标。

否预测到了正确的数值：MSE和MAE

RSS残差平方和，是预测值与真实值之间的差异，也就是从第一种角度来评估我们回归的效力，所以RSS既是我们的损失函数，也是我们回归类模型的模型评估指标之一。但是，RSS有着致命的缺点：它是一个无界的和，可以无限地大，（样本越多，残查平方和越大）。
为了应对这种状况，sklearn中使用RSS的变体，均方误差MSE（mean squared error）来衡量我们的预测值和真实值的差异（这样就消除了由于样本因素而对模型评估的影响。），得到有了平均误差。就可以将其和标签的取值范围在一起比较，以此获得一个较为可靠的评估依据。（得到每一个样本上的平均误差，跟均值比较看相差有多少）在sklearn当中，我们有两种方式调用这个评估指标，

1. 是使用sklearn专用的模型评估模块metrics里的类mean_squared_error，
2. 是调用交叉验证的类cross_val_score并使用里面的scoring参数来设置使用均方误差。
   

1. 均方误差为负：
cross_val_score(reg,X,y,cv=10,scoring=“neg_mean_squared_error”)
因为均方误差本身是一种误差，损失。所以被sklearn划分为模型的一种损失(loss)。在sklearn当中，所有的损失都使用负数表示，因此均方误差也被显示为负数了。真正的均方误差MSE的数值，其实就是neg_mean_squared_error去掉负号的数字。
metrics里可以调出正的均方误差。

MAE：Mean absolute error，绝对均值误差

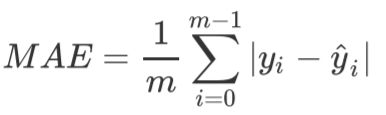
其表达的概念与均方误差完全一致，不过在真实标签和预测值之间的差异外我们使用的是L1范式（绝对值）。现实使用中，MSE和MAE选一个来使用就好了。（MAE比MSE对异常值更加不敏感，有较好的鲁棒性）
在sklearn当中，我们使用命令from sklearn.metrics import mean_absolute_error来调用MAE。
也可以使用交叉验证中的scoring = “neg_mean_absolute_error”，以此在交叉验证时调用MAE。

是否拟合了足够的信息
对于回归类算法而言，只探索数据预测是否准确是不足够的。除了数据本身的数值大小之外，我们还希望我们的模型能够捕捉到数据的”规律“，比如数据的分布规律，单调性等等，而是否捕获了这些信息并无法使用MSE来衡量。
这个图里，如果用MSE来衡量，那么均方误差会很小，但从图上看，很明显这个拟合是不正确的，数据变化的趋势没有拟合。因此不能光从MSE上对回归数据进行评估。

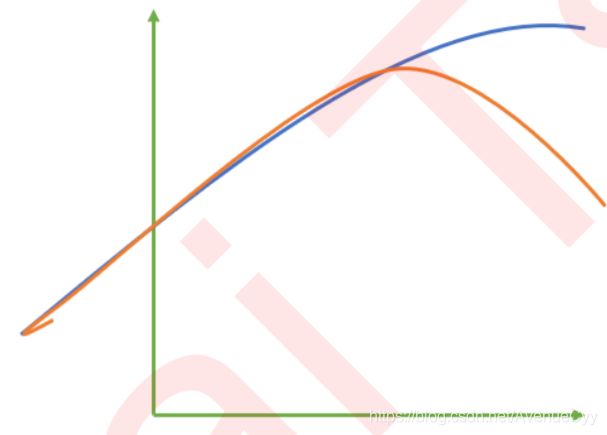
我们使用方差来衡量数据上的信息量。如果方差越大，代表数据上的信息量越多，而这个信息量不仅包括了数值的大小，还包括了我们希望模型捕捉的那些规律。为了衡量模型对数据上的信息量的捕捉，我们定义了R^2来帮助我们:

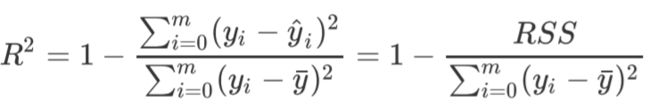
其中分子是MSE，分母是方差，由于都跟样本的倒数有关，所以约掉了。方差的
本质是任意一个y值和样本均值的差异，差异越大，这些值所带的信息越多。
在R^2中，分子是真实值和预测值之差的差值（衡量差异程度），也就是我们的模型没有捕获到的信息总量，分母是真实标签所带的信息量，所以其衡量的是1 - 我们的模型没有捕获到的信息量占真实标签中所带的信息量的比例，所以， R^2越接近1越好。
sklearn中可以使用三种方式来调用，

1. 是直接从metrics中导入r2_score，输入预测值和真实值后打分。
2. 是直接从线性回归LinearRegression的接口score来进行调用。（所有回归模型都有这个接口）
3. 是在交叉验证中，输入"r2"来调用。

from sklearn.metrics import r2_score
r2_score(yhat,Ytest)
r2 = reg.score(Xtest,Ytest)
r2

然而这两种结果不一样。。。

2. 相同的评估指标不同的结果

在我们的分类模型的评价指标当中，我们进行的是一种 if a == b的对比，这种判断和if b == a其实完全是一种概念，所以我们在进行模型评估的时候，从未踩到我们现在在的这个坑里。
然而看R2的计算公式，R2明显和分类模型的指标中的accuracy或者precision不一样，R2涉及到的计算中对预测值和真实值有极大的区别，必须是预测值在分子，真实值在分母，所以我们在调用metrcis模块中的模型评估指标的时候，必须要检查清楚，指标的参数中，究竟是要求我们先输入真实值还是先输入预测值。（在给R^2参数时，要注意输入的是分子【预测值】还是分母【真实值】，输入的顺序不同，结果也不一样。）

3. 负的 R^2
TSS=ESS+RSS不是永远成立的。


关于2()/TSS，()内的公式是否等于0.需要查看线性回归的有关假设条件：

1. 因变量和自变量之间具有线性关系
2. 在重复抽样中，自变量的取值是固定的，即假设x是非随机的
3. 误差项是一个期望为0的随机变量。
4. 对所有x，误差项的方差都相同
5. 误差项服从正态分布.
   其中3条件若不满足，则()内的公式就不会为0.
   

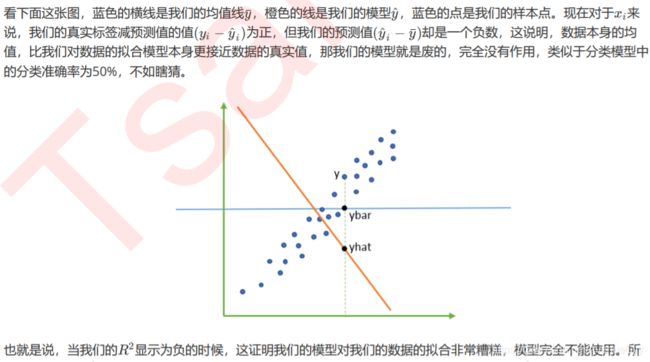
当R^2为负时，首先看建模过程和数据处理过程是否正确，也许你已经伤害了数据本身，也许你的建模过程是存在bug的。如果是集成模型的回归，检查你的弱评估器的数量是否不足，随机森林，提升树这些模型在只有两三棵树的时候很容易出现负的 。如果你检查了所有的代码，也确定了你的预处理没有问题，但你的 R^2 也还是负的，那这就证明线性回归模型不适合你的数据。

另外还有

三、分类问题评估指标

在用准确率衡量分类问题时，对于少数类样本的情况无法进行正常捕捉。（比如，80个正，20个负，如果都预测为正，那么就会有80%的准确率，但这毫无意义，对于信用卡诈骗等，我们更关心少数类样本，因此无法用准确率去衡量）我们往往在寻找捕获少数类的能力和将多数类判错后需要付出的成本的平衡。如果一个模型在能够尽量捕获少数类的情况下，还能够尽量对多数类判断正确，则这个模型就非常优秀了。为了评估这样的能力，我们将引入新的模型评估指标：混淆矩阵和ROC曲线。

混淆矩阵：
混淆矩阵是二分类问题的多维衡量指标体系，在样本不平衡时极其有用。在混淆矩阵中，我们将少数类认为是正例，多数类认为是负例。（真实值永远写在前面）

我们有六个不同的模型评估指标，这些评估指标的范围都在[0,1]之间，以11和00为分子的指标都是越接近1越好，以01和10为分子的指标都是越接近0越好。

3.1 捕捉少数类的艺术：精确度，召回率和F1 score

模型整体效果：准确率
准确率Accuracy，就是所有预测正确的所有样本除以总样本，通常来说越接近1越好。

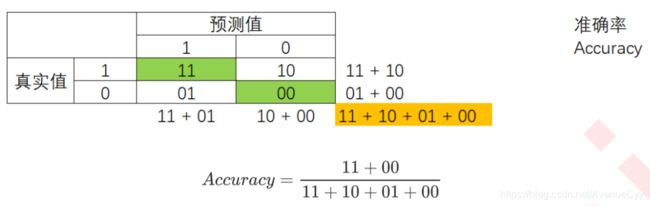
捕捉少数类的艺术：精确度，召回率和F1 score

精确度Precision，又叫查准率，表示所有被我们预测为是少数类的样本中，真正的少数类所占的比例。

精确度越低，则代表我们误伤了过多的多数类（在我们预测为少数类的样本中，既有多数类又有少数类，所以，如果我们的精确度很低，那么就说明有很多本来是多数类的被我们误伤成了少数类，如果我们对多数类判误的代价比较高，即我们希望有很多多数类被判正确，那么我们就不应该误伤多数类，要追求高精确度）。精确度越低，我们对多数类的判断就会越错误。当然了，如果我们的目标是不计一切代价捕获少数类，那我们并不在意精确度。在意多数类是否被判断正确，选择精确度。

召回率Recall，又被称为敏感度(sensitivity)，真正率，查全率
表示所有真实为1的样本中，被我们预测正确的样本所占的比例。

只跟少数类有关。召回率越高，代表我们尽量捕捉出了越多的少数类（这个的前提是所有的类别都为真实的少数类，所以，召回率越高，代表真实的少数类中，我们预测对的比例越大，即捕捉到了更多的少数类），召回率越低，代表我们没有捕捉出足够的少数类。

召回率和精确度是此消彼长的（少数类跟多数类之间很多时候是交叠在一起的，在捕捉少数类的同时，也会误伤一些多数类），两者之间的平衡代表了捕捉少数类的需求和尽量不要误伤多数类的需求的平衡。 是误伤多数类的成本高，还是无法捕捉少数类的成本更高，这之间需要根据业务进行衡量。

为了同时兼顾精确度和召回率，我们创造了两者的调和平均数作为考量两者平衡的综合性指标，称之为F1measure。两个数之间的调和平均倾向于靠近两个数中比较小的那一个数，因此我们追求尽量高的F1 measure，能够保证我们的精确度和召回率都比较高。F1 measure在[0,1]之间分布，越接近1越好。

3.2 判错多数类的考量：特异度与假正率

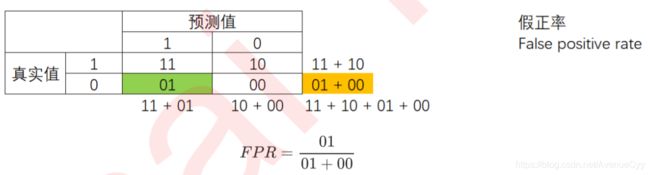
**特异度(Specificity)**表示所有真实为0的样本中，被正确预测为0的样本所占的比例。

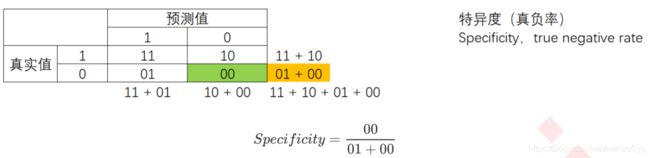
特异度衡量了一个模型将多数类判断正确的能力，而1 - specificity就是一个模型将多数类判断错误的能力，这种能力被计算如下，并叫做假正率（False Positive Rate）。（假正率：有多少多数类被判错了。精确度：有多少少数类被判对了。）

sklearn中由混淆矩阵衍生出的六个模型评估指标：

3.3 ROC曲线以及其相关问题

在我们的六个评估指标中，最重要的是召回率，然后是精确率，以及假正率FPR。

假正率有一个非常重要的应用：我们在追求较高的Recall的时候，Precision会下降，就是说随着更多的少数类被捕捉出来，会有更多的多数类被判断错误，但我们很好奇，随着Recall的逐渐增加，模型将多数类判断错误的能力如何变化呢？我们希望理解，我每判断正确一个少数类，就有多少个多数类会被判断错误。假正率（在多数类中，有多少多数类被判错了）正好可以帮助我们衡量这个能力的变化。（Recall越大，少数类被捕捉的也就越多，同时，也会误伤到更多的多数类，误伤意味着有更多的多数类被判错误，而FPR是衡量多数类中，有多少多数类被判错误，所以FPR也会随着Recall增加而增加。如果Recall比FPR增加的快，证明判断出一个少数类的代价不是很大；如果FPR比Recall增加的快，那就说明判断出一个少数类要牺牲更多的多数类）

相对的，Precision无法判断这些判断错误的多数类在全部多数类中究竟占多大的比例，所以无法在提升Recall的过程中也顾及到模型整体的Accuracy。因此，我们可以使用Recall和FPR之间的平衡，来替代Recall和Precision之间的平衡，让我们衡量模型在尽量捕捉少数类的时候，误伤多数类的情况如何变化，这就是我们的ROC曲线衡量的平衡。

ROC曲线，全称The Receiver Operating Characteristic Curve。这是一条以不同阈值下的假正率FPR为横坐标，不同阈值下的召回率Recall为纵坐标的曲线。

概率(probability)与阈值(threshold)：
概率：样本点判别为某一类的概率
阈值：人为设定的数，若概率大于阈值，则会被设定为某一类。

要理解概率与阈值，最容易的状况是来回忆一下我们用逻辑回归做分类的时候的状况。逻辑回归的predict_proba接口对每个样本生成每个标签类别下的似然（类概率）。对于这些似然，逻辑回归天然规定，当一个样本所对应的这个标签类别下的似然大于0.5的时候，这个样本就被分为这一类。在这个过程中，0.5就被称为阈值。
通过不断调整阈值，可以达到不同Recall和FPR。通常来说，降低阈值能够提升Recall.

但是注意，并不是升高阈值，就一定能够增加或者减少Recall，一切要根据数据的实际分布来进行判断。而要体现阈值的影响，首先必须的得到分类器在少数类下的预测概率。对于逻辑回归这样天生生成似然的算法和朴素贝叶斯这样就是在计算概率的算法，自然非常容易得到概率，但对于一些其他的分类算法，比如决策树，比如SVM，他们的分类方式和概率并不相关。

决策树有叶子节点，一个叶子节点上可能包含着不同类的样本。假设一个样本被包含在叶子节点a中，节点a包含10个样本，其中6个为1，4个为0，则1这个正类在这个叶子节点中的出现概率就是60%，类别0在这个叶子节点中的出现概率就是40%。对于所有在这个叶子节点中的样本而言，节点上的1和0出现的概率，就是这个样本对应的取到1和0的概率，大家可以去自己验证一下。但是思考一个问题，由于决策树可以被画得很深，在足够深的情况下，决策树的每个叶子节点上可能都不包含多个类别的标签了，可能一片叶子中只有唯一的一个标签，即叶子节点的不纯度为0，此时此刻，对于每个样本而言，他们所对应的“概率”就是0或者1了。这个时候，我们就无法调节阈值来调节我们的Recall和FPR了。
所以，如果我们有概率需求，我们还是会优先追求逻辑回归或者朴素贝叶斯。不过其实，SVM也可以生成概率。

SVM实现概率预测：重要参数probability，接口predict_proba以及
decision_function

越靠近决策边界的点，判别为某一类的概率越模糊，而越远离边界，判别为某一类的概率就越大。点到决策边界的距离衡量了样本归属于某一类别的可能性。接口decision_function返回的值也因此被我们认为是SVM中的置信度（confidence）。SVC有重要参数probability。

建立ROC曲线的根本目的是找寻Recall和FPR之间的平衡，让我们能够衡量模型在尽量捕捉少数类的时候，误伤多数类的情况会如何变化。
ROC曲线如果是凹的，那么把正负类调整一下就行。越接近中间的线，越糟糕。

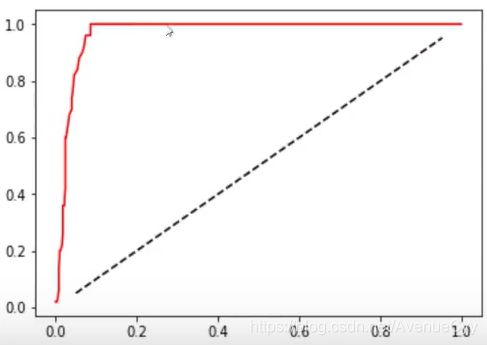
横坐标是FPR，代表着模型将多数类判断错误的能力，纵坐标Recall，代表着模型捕捉少数类的能力，所以ROC曲线代表着，随着Recall的不断增加，FPR如何增加。
我们希望随着Recall的不断提升，FPR增加得越慢越好，这说明我们可
以尽量高效地捕捉出少数类，而不会将很多地多数类判断错误。所以，我们希望看到的图像是，纵坐标急速上升，横坐标缓慢增长，也就是在整个图像左上方的一条弧线。这代表模型的效果很不错，拥有较好的捕获少数类的能力。
仅从曲线判断不太靠谱，需要一个数值来衡量曲线靠近左上角的程度。AUC面积，它代表了ROC曲线下方的面积，这个面积越大，代表ROC曲线越接近左上角，模型就越好。AUC面积的计算比较繁琐，因此，我们使用sklearn来帮助我们。

sklearn中的ROC曲线和AUC面积：
在sklearn中，我们有帮助我们计算ROC曲线的横坐标假正率FPR，纵坐标Recall和对应的阈值的类sklearn.metrics.roc_curve。同时，我们还有帮助我们计算AUC面积的类sklearn.metrics.roc_auc_score。

在无法获取模型概率的情况下，其实不必强行使用概率，如果有置信度，那也使可以完成我们的ROC曲线。

利用ROC曲线找出最佳阈值：
ROC曲线反
应的是recall增加的时候FPR如何变化，也就是当模型捕获少数类的能力变强的时候，会误伤多数类的情况是否严重。我们的希望是，模型在捕获少数类的能力变强的时候，尽量不误伤多数类，也就是说，随着recall的变大，FPR的大小越小越好。所以我们希望找到的最有点，其实是Recall和FPR差距最大的点。这个点，又叫做约登指数。

四、聚类问题评估指标

不同于分类模型和回归，聚类算法的模型评估不是一件简单的事。
在分类中，有直接结果（标签）的输出，并且分类的结果有正误之分，所以我们使用预测的准确度，混淆矩阵，ROC曲线等等指标来进行评估，但无论如何评估，都是在”模型找到正确答案“的能力。
而回归中，由于要拟合数据，我们有SSE均方误差，有损失函数来衡量模型的拟合程度。但这些衡量指标都不能够使用于聚类。

4.1 真实标签已知

4.2 真实标签未知

聚类，是完全依赖于评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。（希望b越大越好，a越小越好。）取值范围为(-1,1)，s大于0，说明聚类效果还可以，越接近1，聚类效果就越好。越接近0，说明这两个簇没有什么区别，可以合并为一个簇。



另外，可用卡林斯基-哈拉巴斯指数（Calinski-Harabaz Index，简称CHI，也被称为方差比标准），戴维斯-布尔丁指数（Davies-Bouldin）以及权变矩阵（Contingency Matrix）等。
其中sklearn.metrics.calinski_harabaz_score (X, y_pred)比较常用，由于是矩阵运算，比较快。
们通常会绘制轮廓系数分布图和聚类后的数据分布图来选择我们的最佳n_clusters。代码请参考上面的机器学习菜菜。
学习曲线不能解决轮廓系数在聚类上的问题，因为如果不分析每一类聚出来的效果，很难说最高的轮廓系数的值就是最佳聚类。