优化算法专题一：SA模拟退火算法及Python代码实操

备注：本文参照《进化优化算法–基于仿生和种群的计算机智能方法》整理而得，并在文末附上Python代码

1 爬山算法

模拟退火的核心与爬山算法相似，首先介绍一下爬山算法。
爬山算法：从当前的节点开始，和周围的邻居节点的值进行比较。 如果当前节点较优，那么返回当前节点；反之就用更优的邻居节点，来替换当前节点，从而实现向山峰的高处攀爬的目的。
模拟退火：与爬山算法不同的是，当邻居节点劣于当前节点时，以一定的概率接受该邻居节点。

2 自然退火

晶格状物质特性：晶格体结构是液体或固体中原子或分子的一种排列，常见的晶格体有石英、冰和盐。高温让物质的能量增加，从而导致很多的振动和混乱；而当温度降低时，晶格状物质会进入一个更加有序的状态。物质经过多次加热和冷却，每次会进入不同的均衡状态。
退火：给物质加温并让它冷却到再结晶的过程。
自然退火目的：让晶体进入低能量组态，晶格状结构更有秩序。

3 模拟退火算法

模拟退火算法，模拟自然退火让晶体进入低能量组态这个过程。对于最小化问题，从候选解s开始，也从较高的温度开始，较高的温度使得候选解更有可能跳转到另一个组态（接受概率）。随机生成一个备选的候选解r并评估其费用：
上式，当r的费用小于s的费用时，以1的概率接受r作为下一时刻的候选组态；当r的费用大于或等于s的费用时，以一定的概率接受r作为下一时刻的候选组态。此时，E（s）

自然退火	模拟退火
原子组态	候选解
温度	探索搜索空间的趋势
冷却	降低探索的趋势
原子组态的改变	候选解的改变

4 主要参数

伪代码：最小化f(x)的基本模拟退火算法，函数U[0,1]返回[0,1]上均匀分布的随机数。

主要调试参数：

参数	性能影响	设置
初始温度T	为探索和开发的相对重要性设定上界	过低：不能有效地探索搜索空间； 过高：收敛时间长
冷却函数a(T)	控制收敛速率	算法开始：多探索少开发； 算法结束：多开发少探索
候选解生成策略	影响算法性能	随机 or 生成比当前组态更好的组态

5 冷却调度

6 候选解生成

简易的候选解生成方式，即在搜索空间中随机选择一个点。但在算法收敛到一个较好的解后，可以期望当前的候选解x0比搜索空间中绝大多数的点要好。此时，随机生成候选解可能效果不好。作为一般规则，让生成的候选解偏向当前的候选解x0。因此，可以选用以x0为中心的高斯分布或者柯西分布来生成更积极的候选解。

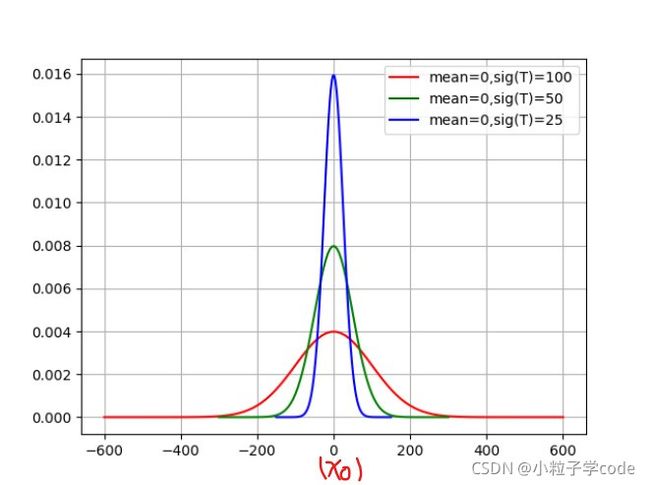
上图，新生成的候选解x~N(x0,T^2)。随着算法迭代，温度会下降，x会更大概率地落在x0附近，即搜索范围逐渐收窄（蓝色线）。

7 代码案例练习

优化函数案列


代码实操

import numpy as np
import random
import copy
import matplotlib.pyplot as plt
import math
from random import Random

class SAOptimization:
    '''
    The class for SA optimization algorithm
    '''
    def __init__(self, initial_Temp, cooling_Func, bound, vardim, num_iter):
        '''
        initial_Temp: initial temperature
        cooling_Func: choosing cooling function: linear, exp, inverse_cooling, log, inverse_linear
        candidate_Gene: choosing the way of generating candidate X
        bound: boundaries of variables
        vardim: the dimension of the vector
        num_iter: number of iteration
        '''
        self.initial_Temp = initial_Temp
        self.cooling_Func = cooling_Func
        self.bound = bound
        self.vardim = vardim
        self.num_iter = num_iter
        
		#储存整个过程中最好的solution及fitness
        self.best_solution = np.zeros((1, self.vardim))
        self.best_fitness = 1e10
        self.T = 1e10 #温度设置
        self.k = 0 #迭代次数
        self.trace = [] #记录每一次迭代的fitness值

    # generate the initial solution within the bound
    def initialize(self):
        rnd = np.random.random(size=self.vardim) #生成0-1之间的数值
        self.solution = np.zeros(self.vardim)
        for i in range(0, self.vardim):
            self.solution[i] = self.bound[0] + (self.bound[1] - self.bound[0]) * rnd[i]
        self.T = self.initial_Temp

    # evaluation of the fitnesses
    def evaluate(self):
        a = (-0.2 / self.vardim) * np.sum(self.solution * self.solution)
        b = [math.cos(2 * math.pi * i) for i in self.solution]
        c = (1 / self.vardim) * sum(b)
        self.fitness = 20 + math.exp(1) - 20 * math.exp(a) - math.exp(c)
	
	# cooling function
    def cooling(self):
        if self.cooling_Func == 'linear':
            b = 3
            Tmin = 10
            self.T = max(self.T - b, Tmin)
        if self.cooling_Func == 'exp':
            b = 0.9994
            self.T = b * self.T
        if self.cooling_Func == 'inverse_cooling':
            b = 0.001
            self.T = self.T / (1 + b * self.T)
        if self.cooling_Func == 'log':
            c = 100
            self.T = c / math.log(1 + self.k)
        if self.cooling_Func == 'inverse_linear':
            self.T = self.initial_Temp/ self.k

    #iteration process of SA algorithm
    def solve(self):
        #初始值，并将初始值的fitness赋值到best_fitness
        self.initialize()
        self.evaluate()
        self.best_fitness = self.fitness
        self.best_solution = copy.deepcopy(self.solution)

        #开始生成新的solution
        while self.k < self.num_iter:
        	# 储存当前的fitness和solution
            fit = self.fitness
            sol = copy.deepcopy(self.solution)
            
            # （为了约束解的取值范围）由高斯随机分布产生的随机数r，有0.9973的概率落在（0-3T，0+3T），将之映射到（-1,1）
            r = (1-(-1))/(3*self.T-(-3)*self.T) * Random().gauss(0, self.T)

            for i in range(self.vardim):
                if self.solution[i] * (1 + r) > self.bound[1]:
                    self.solution[i] = self.bound[1]
                if self.solution[i] * (1 + r) < self.bound[0]:
                    self.solution[i] = self.bound[0]
                else:
                    self.solution[i] = self.solution[i] * (1 + r)
			# 计算新solution对应的fitness值，并储存到fit_new中
            self.evaluate()
            fit_new = self.fitness
			
			# 如果新的fitness大于当前fitness，则以1的概率接受新的solution（之前已储存到全局变量self.solution中），作为下一时刻的候选组态
            if fit_new < fit:
                if fit_new < self.best_fitness:
                    self.best_fitness = self.fitness
                    self.best_solution = copy.deepcopy(self.solution)
                    
			#否则，则以一定概率接受新的solution
            else:
                a = np.random.random() #随机生成0-1之间的数值
                #如果a大于某一指定的概率，即不接受新的solution，用之前存储的sol（当前solution），作为下一时刻的候选组态。需将更新后的self.solution换回更新前的solution。
                if a > math.exp((fit - fit_new)/self.T):
                    self.solution = copy.deepcopy(sol)
                    self.fitness = fit
            self.trace.append(self.fitness)
            self.k = self.k + 1
            # 调用冷却函数，降低温度T
            self.cooling()

        print("Optimal function value is: %f; " %
              self.best_fitness)
        print("Optimal solution is:")
        print(self.best_solution)
        self.printResult()

    def printResult(self):
        '''
        plot the result of the SA algorithm
        '''
        x = np.arange(0, 100)
        y1 = self.trace[0:100]
        plt.plot(x, y1, 'r', label='optimal value')
        plt.xlabel("Iteration")
        plt.ylabel("function value")
        plt.title("SA algorithm for function optimization")
        plt.legend()
        plt.show()

if __name__ == "__main__":
    bound = [-30,30]
    sa = SAOptimization(100, 'inverse_cooling', bound, 20, 10000)
    sa.solve()

Results：

最小结果及最优解：

Optimal function value is: -0.000000; 
Optimal solution is:
[-1.31634338e-09 -3.74406660e-09 -2.94534205e-09 -2.40885869e-09
 -3.40915980e-09 -6.98357748e-11 -5.37607824e-09 -5.01749403e-09
 -8.58107969e-11  6.49798039e-09 -5.20549434e-09  6.01598851e-09
 -5.43241432e-09 -5.58455711e-09  4.49673641e-09 -4.49990081e-09
  2.76502072e-09  8.62887618e-10  1.58799297e-09 -5.23363203e-09]

备注：整理自《进化优化算法–基于仿生和种群的计算机智能方法》