Python数据分析与挖掘——使用Matplotlib绘制直方图
1. 使用hist绘制频数直方图
在Matplotlib中有一个专门绘制直方图的函数hist(),用来显示一组数据的分布情况。
使用hist()函数,无需对数据进行分拣整理,即可自动生成直方图。使用格式如下:
plt.hist(x, bins)
# 参数名基于官方文档声明参数x:用于绘制直方图的一维数组,列表或者DataFrame的列向量形式。
参数bins:分两种情况:
(1)一个整数,按照数组的最小取值范围(即以数组的最小值和最大值作为区间的两端点)均匀分为若干组。
(2)数字列表,以列表的各个数字作为分组的边界点。
例如,随机生成一个含有1000个元素的服从标准正态分布的数组,绘制直方图,代码如下:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt # 导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.figure(figsize=(7,5))
data = np.random.randn(1000) # 1000个服从标准正态分布的随机数
plt.hist(data, 10) # 分成10组,结果如图1
plt.show()
# div = [-4, -3.5, -3, ..., 3, 3.5, 4]
div = []
x = -4
while x <= 4:
div.append(x)
x += 0.5
plt.hist(data, div) # 指定分界点,结果如图2
plt.show()
得到的直方图如下:
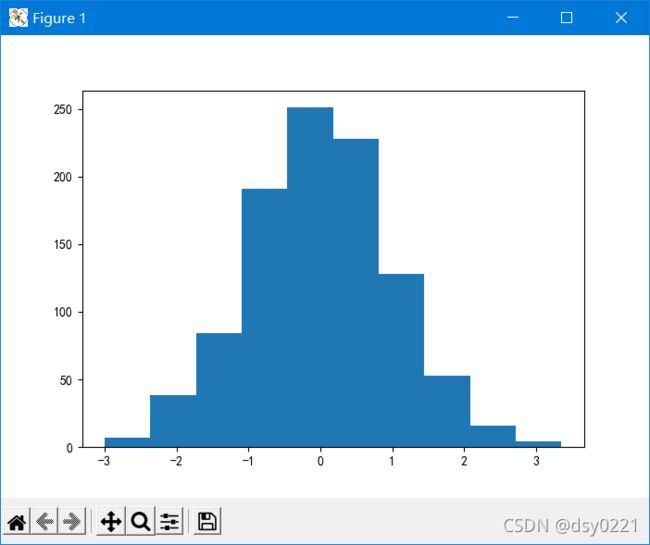 图1
图1  图2
图2
2. 绘制频率直方图
Matplotlib中的hist()函数,实际上是在统计落在各区间的数据个数(相当于放置了若干个桶,把这些数据按照所落在的区间分别放进相应的桶内)并生成直方图,因此纵坐标是频数。
如果要绘制同样的直方图,但是要把纵坐标表示成频率或者频率与各组间距之比,需要先对数据进行分拣处理,然后以条形图(bar)形式输出结果。
以条形图的形式输出,有两种方式:
(1)直接用plt.bar()函数,使用格式:
plt.bar(x, height)
# 参数名基于官方文档声明x为横坐标的标签,height为纵坐标的数值,二者均为列表或者DataFrame的列向量,且相同下标一一对应。
(2)封装成DataFrame对象后使用内置方法plot(),并指定kind参数为“bar”。只能使用该DataFrame对象中指定的一列数据,并且要在封装对象时指定索引列,以索引列作为横坐标的标签。使用格式:
df[col].plot(kind = "bar")对于上一节的例子,采用plt.bar()函数绘制直方图的代码如下:
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt # 导入图像库
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.figure(figsize=(18,5))
data = np.random.randn(1000) # 1000个服从正态分布的随机数
# div = [-4, -3.5, -3, ..., 3, 3.5, 4]
div = [-4]
x = [] # 横坐标,分组
y = [] # 纵坐标,频率,初始化为与分组同等数量的0
i = -3.5
j = 1
while i <= 4:
div.append(i)
x.append("["+str(div[j-1])+","+str(div[j])+")")
y.append(0)
i += 0.5
j += 1
# 分拣数据
for item in data:
for i in range(0, len(div) - 1):
if item >= div[i] and item < div[i + 1]:
y[i] += 1
break
# 转换为频率
for i in range(len(y)):
y[i] = round(y[i] / 1000, 3) * 100 # 化为百分比
plt.bar(x, y)
plt.xlabel("分组")
plt.ylabel(r"频率/%")
plt.show()如果封装成DataFrame对象,使用内置方法plot()并指定kind参数为“bar”,则上面代码的后四行应改为:
import pandas as pd
df = pd.DataFrame(y, index=x)
df.plot(kind="bar")
plt.xlabel("分组")
plt.ylabel(r"频率/%")
plt.show()结果如图3:(此为采用第一种方法得到的结果,第二种方法得到的形状相同,只是横坐标的标签逆时针旋转90度)
 图3
图3
3. 绘制频率分布直方图(纵轴为频率/组距)
将上一节绘制直方图的代码“# 转换为频率”以下的部分改成下列代码,即可将纵轴设置为频率与各分组间距之比,即频率分布直方图:
# 转换为频率/组距
for i in range(len(y)):
y[i] = round(y[i] / 1000 / 0.5, 3) # 频率/组距,保留三位小数
plt.bar(x, y)
plt.xlabel("分组")
plt.ylabel("频率/组距")
plt.show()# 转换为频率/组距
for i in range(len(y)):
y[i] = round(y[i] / 1000 / 0.5, 3) # 频率/组距,保留三位小数
df = pd.DataFrame(y, index=x)
df.plot(kind="bar")
plt.xlabel("分组")
plt.ylabel("频率/组距")
plt.show()结果如图4:
 图4
图4