Python多分类问题pr曲线绘制（含代码）

研究了三天的多分类pr曲线问题终于在昨天晚上凌晨一点绘制成功了！！
现将所学所感记录一下，一来怕自己会忘可以温故一下，二来希望能给同样有疑惑的铁子们一些启迪！

下图为我画的pr曲线，因为准确度超过了97%，所以曲线很饱和。

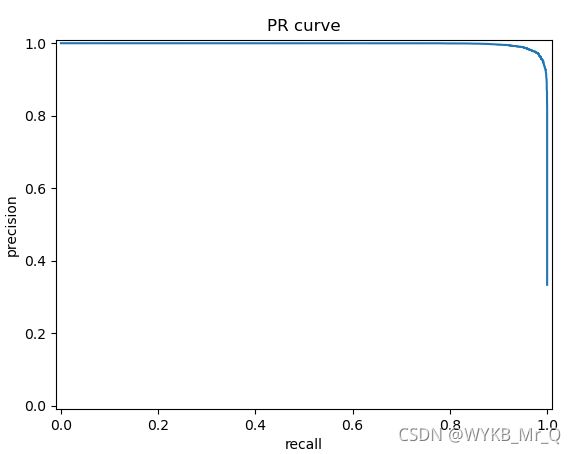
首先了解一下二分类中的pr曲线是怎么画的？

“p” 是precition，是查准率，也是我们常用到的准确率。
“r” 是recall，是查全率，也叫召回率。

​
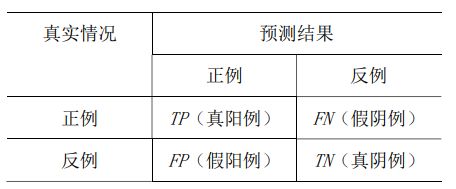
上图为测试结果的混淆矩阵，表示一个数据集上的所有测试结果。
其中竖列均为测试结果，即分类器预测概率大于0.5为正类，小于0.5即为负类。
横列表示groundtruth，即真实的类别。

TP 表示正确分出正例的数量；
FN 表示把正例错分为反例的数量；
TN 表示正确分出反例的数量；
FP表示把反例错分为正例的数量。

准确率： P = TP /（TP+FP）
召回率： R = TP / (TP+FN)

上面是对精确率和召回率的简单介绍，下面进入正题！

---

我们根据预测结果只能够求出一组 “p” 值和 “r” 值，那是因为我们默认把阈值设置成了0.5，大于0.5就是正例，反之就是反例。

假如说我们有一组飞机和大雁的图片集，我们想从中找出飞机的图片。
此时飞机就是正例，大雁或者说其它就是反例。
之后我们算出所有图片经测试为飞机的概率，（当然这里有两组概率，为飞机或者为大雁，这时我们不管为大雁的概率，只关注为飞机的概率），并从大到小进行排序。

蓝色虚线是我们设置阈值为0.5时候的分类情况，大于0.5是测试为飞机的概率，小于0.5是测试不为飞机的概率。

当阈值变小时，更多样本会被测试成飞机，虚线下移。假设取极限，阈值为0，那么所有样本都会被预测为飞机，召回率最大，为1；而精确率为 5/10 等于0.5。同理，阈值变大，虚线上移，精确率会变高，但召回率反而变低。

在设置阈值的时候，有两种方法：
1、从0-1之间按照等间隔设置，比如0，0.1，0.2，…，0.9，1.0。这样能得到10组 “p” “r” 值。当然也可以把间隔设置的小一点，可以得到更多组 “p” “r” 值。
2、把所有样本的概率预测值从小到大排序去重，并以此数列分别为阈值，进行计算 “p" “r” 值，可以得到更多组 “p” “r” 值。

绘制多分类的pr曲线

首先多分类方法无法绘制标准的pr曲线。

对于多分类问题，针对每一种类别都可以得到相对应的精确率和召回率，这样多分类问题就可以得到多组 “p” “r” 值，（P1, R1), (P2, R2), …, (Pn, Rn)。

对此计算平均值，就可以得到一组平均精确率和召回率，又叫做 "宏精确率” （macro-P）和 “宏召回率”(macro-R)。由此画得的曲线应该叫做 “宏pr曲线”！

因此我们需要先确定出数据集的测试结果。包括测试集的ground-truth类别，预测类别，以及对于每个测试样本的预测概率，保存成.txt文件。下图为.txt文件中的部分数据：

2 2 0.0000 0.0000 1.0000
0 0 0.9748 0.0252 0.0000
1 1 0.0000 1.0000 0.0000
2 1 0.0000 0.7629 0.2371
0 0 0.9999 0.0001 0.0000
1 1 0.0000 0.9996 0.0004
2 2 0.0000 0.0360 0.9640
0 0 0.9954 0.0046 0.0000
1 1 0.0000 0.9997 0.0003
2 2 0.0000 0.0000 1.0000
1 1 0.0000 1.0000 0.0000
1 1 0.0000 1.0000 0.0000
0 0 0.9972 0.0028 0.0000
1 1 0.0000 1.0000 0.0000

以三分类为例，上图是从左到右分别是标签、预测类别、以及预测概率（三类别，因此有三个概率），这个根据自己的分类的情况，从预测结果中提取出来就行。

这是提取.txt文件的参考代码：

# 提取.txt文件的参考代码  clses是分类标签列表，preds是预测结果列表，pred_score是预测得分。
print("Saving files to txt....")
with open("pr_curve.txt", 'w') as pr:
    for i in range(len(clses)):
        pr.write(str(clses[i]) + " " + str(preds[i]) + " " + str(format(pred_score[i][0], '.4f')) + " " +
                str(format(pred_score[i][1], '.4f')) + " " + str(format(pred_score[i][2], '.4f')) + "\n")
print("All files have been written!")

下面是计算“宏pr值”以及绘制pr曲线的代码（含注释）：

import numpy as np
import matplotlib.pyplot as plt

score_path = "./pr_curve.txt"  # 文件路径
with open(score_path, 'r') as f:
    files = f.readlines()      # 读取文件

lis_all = []
for file in files:
    _, _, s1, s2, s3 = file.strip().split(" ")
    lis_all.append(s1)
    lis_all.append(s2)
    lis_all.append(s3)
lis_order = sorted(set(lis_all))   # 记录所有得分情况，并去重从小到大排序，寻找各个阈值点

macro_precis = []
macro_recall = []

for i in lis_order:

    true_p0 = 0         # 真阳
    true_n0 = 0         # 真阴
    false_p0 = 0        # 假阳
    false_n0 = 0        # 假阴

    true_p1 = 0
    true_n1 = 0
    false_p1 = 0
    false_n1 = 0

    true_p2 = 0
    true_n2 = 0
    false_p2 = 0
    false_n2 = 0
    for file in files:
        cls, pd, n0, n1, n2 = file.strip().split(" ")       # 分别计算比较各个类别的得分，分开计算，各自为二分类，
                                                            # 最后求平均，得出宏pr

        if float(n0) >= float(i) and cls == '0':               # 遍历所有样本，第0类为正样本，其他类为负样本，
            true_p0 = true_p0 + 1                              # 大于等于阈值，并且真实为正样本，即为真阳，
        elif float(n0) >= float(i) and cls != '0':             # 大于等于阈值，真实为负样本，即为假阳；
            false_p0 = false_p0 + 1                            # 小于阈值，真实为正样本，即为假阴
        elif float(n0) < float(i) and cls == '0':
            false_n0 = false_n0 + 1

        if float(n1) >= float(i) and cls == '1':                # 遍历所有样本，第1类为正样本，其他类为负样本
            true_p1 = true_p1 + 1
        elif float(n1) >= float(i) and cls != '1':
            false_p1 = false_p1 + 1
        elif float(n1) < float(i) and cls == '1':
            false_n1 = false_n1 + 1

        if float(n2) >= float(i) and cls == '2':                # 遍历所有样本，第2类为正样本，其他类为负样本
            true_p2 = true_p2 + 1
        elif float(n2) >= float(i) and cls != '2':
            false_p2 = false_p2 + 1
        elif float(n2) < float(i) and cls == '2':
            false_n2 = false_n2 + 1

    prec0 = (true_p0+0.00000000001) / (true_p0 + false_p0 + 0.00000000001)      # 计算各类别的精确率，小数防止分母为0
    prec1 = (true_p1+0.00000000001) / (true_p1 + false_p1 + 0.00000000001)
    prec2 = (true_p2+0.00000000001) / (true_p2 + false_p2 + 0.00000000001)

    recall0 = (true_p0+0.00000000001)/(true_p0+false_n0 + 0.00000000001)        # 计算各类别的召回率，小数防止分母为0
    recall1 = (true_p1+0.00000000001) / (true_p1 + false_n1+0.00000000001)
    recall2 = (true_p2+0.00000000001)/(true_p2+false_n2 + 0.00000000001)

    precision = (prec0 + prec1 + prec2)/3
    recall = (recall0 + recall1 + recall2)/3               # 多分类求得平均精确度和平均召回率，即宏macro_pr
    macro_precis.append(precision)
    macro_recall.append(recall)

macro_precis.append(1)
macro_recall.append(0)
print(macro_precis)
print(macro_recall)

x = np.array(macro_recall)
y = np.array(macro_precis)
plt.figure()
plt.xlim([-0.01, 1.01])
plt.ylim([-0.01, 1.01])
plt.xlabel('recall')
plt.ylabel('precision')
plt.title('PR curve')
plt.plot(x, y)
plt.show()

代码是针对三分类写的，当然五分类多分类等，在代码里添加修改就可以了。

首先是了解pr曲线原理；
然后得到包含标签、预测类别和预测得分的.txt文件；
最后绘制pr曲线。

到这里多分类绘制pr曲线就介绍完毕了，早上写到了10点半，主要是想赶紧记下来，不然后面自己肯定又会懒惰了。

编写本文主要参考了：
周志华的《机器学习》西瓜书
https://sanchom.wordpress.com/tag/average-precision/
https://blog.csdn.net/hysteric314/article/details/54093734

日常学习记录，一起交流讨论吧！侵权联系~