【智能优化算法 】基于适应度相关优化器求解单目标优化问题附matlab代码
1 内容介绍
在本文中,提出了一种新的群体智能算法,称为适应度依赖优化器(FDO)。蜂拥而至的繁殖过程及其集体决策启发了这种算法。它与蜜蜂算法或人工蜂群算法没有算法联系。值得一提的是,FDO 被认为是一种基于粒子群优化(PSO)的算法,它通过增加速度(步速)来更新搜索代理的位置。但是,FDO 计算速度的方式不同;它使用问题适应度函数值来产生权重,这些权重在探索和利用阶段指导搜索代理。在本文中,介绍了 FDO 算法,并解释了该想法背后的动机。此外,在一组 19 个经典基准测试函数上对 FDO 进行了测试,并将结果与 PSO、遗传算法(GA)和蜻蜓算法(DA)三种著名算法进行了比较;此外,FDO 在 IEEE 进化计算基准测试函数大会(CEC-C06,2019 竞赛)[1] 上进行了测试。将结果与三种现代算法进行比较:(DA)、鲸鱼优化算法 (WOA) 和 salp swarm 算法 (SSA)。 FDO 结果在大多数情况下显示出更好的性能,而在其他情况下则显示出比较结果。此外,使用 Wilcoxon 秩和检验对结果进行统计检验,以显示结果的显着性。同样,探索和开发阶段的 FDO 稳定性也使用不同的标准测量进行验证和性能证明。最后,将 FDO 应用到实际应用中作为其可行性的证据。
2 仿真代码
% 此函数包含基准的完整信息和实现
% 文中表1、表2、表3中的函数
% lb是下限: lb=[lb_1,lb_2,...,lb_d]
% up是上限: ub=[ub_1,ub_2,...,ub_d]
% dim是变量的数量(问题的维度)
function [lb, ub, dim, fobj] = Get_Functions_details(F)
switch F
case 'F1'
% Sphere
fobj = @F1;
lb=-100;
ub=100;
dim=30;
case 'F2'
% Schwefel 2.22
fobj = @F2;
lb=-10;
ub=10;
dim=50;
case 'F3'
% Schwefel 1.2
fobj = @F3;
lb=-100;
ub=100;
dim=100;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=30;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=30;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=30;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=30;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=30;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=30;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=30;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=30;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=30;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=30;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
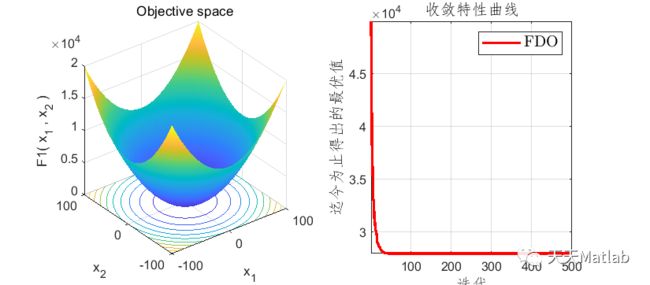
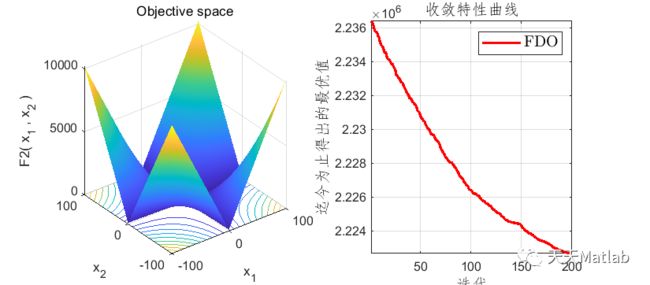
3 运行结果
4 参考文献
[1] Abbas D K , Rashid T A , Bacanin K , et al. Using Fitness Dependent Optimizer for Training Multi-layer Perceptron[J]. 2022.
博主简介:擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真,相关matlab代码问题可私信交流。
部分理论引用网络文献,若有侵权联系博主删除。