【机器学习-西瓜书】-第3章-线性回归-学习笔记-上
3.1基本形式
通过属性的线性组合来进行预测的函数,即
f ( x ) = w 1 x 1 + w 2 x 2 + … + w d x d + b f(\boldsymbol{x})=w_{1} x_{1}+w_{2} x_{2}+\ldots+w_{d} x_{d}+b f(x)=w1x1+w2x2+…+wdxd+b
f ( x ) = w T x + b f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b f(x)=wTx+b
线性模型具有很好的可解释性(可理解性),通过权重的大小可以判断属性的重要性
3.2线性回归
线性回归(linear regression)
学得一个线性模型尽可能准确地预测实值输出标记
数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D=\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\} D={(x1,y1),(x2,y2),…,(xm,ym)}
x i = ( x i 1 x i 2 ; … ; x i d ) , y i ∈ R \boldsymbol{x}_{i}=\left(x_{i 1}\right.\left.x_{i 2} ; \ldots ; x_{i d}\right), y_{i} \in \mathbb{R} xi=(xi1xi2;…;xid),yi∈R
属性的处理
线性回归中处理的属性都是实数值,所以针对离散属性需要转换
- 属性间存在"序"(order)关系
- 通过连续化将其转化为连续值
- 例:高度的高中低,可转换为{1.0,0.5,0.0}
- 通过连续化将其转化为连续值
- 属性间不存在序关系
- k个属性值,直接转换为k维向量
- 例:瓜类的取值,西瓜、南瓜、黄瓜,转换为(0,0,1),(0,1,0),(1,0,0)
无序属性直接连续化处理,可能会引入不恰当的序关系
线性回归 v.s. 正交回归
线性回归最小化蓝色误差
正交回归最小化红色误差
线性回归的公式推导
下面以单属性为例
线性回归的目标
f ( x i ) = w x i + b , 使得 f ( x i ) ≃ y i f\left(x_{i}\right)=w x_{i}+b, \text { 使得 } f\left(x_{i}\right) \simeq y_{i} f(xi)=wxi+b, 使得 f(xi)≃yi
最小二乘法理解
- 基于均方误差最小化来进行模型求解
- 均方误差也称为平方损失
- 有很好的集合意义,对应了欧几里得距离(欧式距离)
- 思想
- 试图找到一条直线,使得样本到直线上的欧式距离之和最小
- 应用范围
- 用途很广,不仅限于线性回归
两个角度看最小二乘法
- 数学角度:最小化均方误差
- 集合角度:最小化点到直线平行y轴的距离
优化公式
( w ∗ , b ∗ ) = arg min ( w , b ) ∑ i = 1 m ( f ( x i ) − y i ) 2 = arg min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 \begin{aligned} \left(w^{*}, b^{*}\right) &=\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2} \\ &=\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} \end{aligned} (w∗,b∗)=(w,b)argmini=1∑m(f(xi)−yi)2=(w,b)argmini=1∑m(yi−wxi−b)2
其中 w ∗ w^* w∗, b ∗ b^* b∗分别代表 w w w和 b b b的解
补充说明
- arg: argument
- min: minimum
a r g m i n arg\text{ }min arg min v.s. m i n min min
- a r g m i n arg\text{ }min arg min 代表使目标函数达到最小值的参数取值
- m i n min min 代表的是目标函数的最小值
min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 s.t. w > 0 b < 0 \begin{array}{l} \min _{(w, b)} \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} \\ \text { s.t. } w>0 \\ \quad b<0 \end{array} min(w,b)∑i=1m(yi−wxi−b)2 s.t. w>0b<0
- 在指定范围内求目标函数的最小值
- s . t . s.t. s.t.是subject to, 受约束于,即为约束条件
求解 w w w和 b b b使 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 E_{(w, b)}=\sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} E(w,b)=∑i=1m(yi−wxi−b)2最小化的过程,称为线性回归模型的最小二乘"参数估计"
极大似然估计理解
一个变量由很多独立变量加和之后得到的情况下,可以认为该变量符合正态分布
针对线性回归,假设
y = w x + b − ϵ y=w x+b-\epsilon y=wx+b−ϵ
其中 ϵ \epsilon ϵ代表的是不受控制的随机误差,通常假设服从均值为0的正态分布 ϵ ∼ N ( 0 , σ 2 ) \epsilon \sim N\left(0, \sigma^{2}\right) ϵ∼N(0,σ2)
所以 ϵ \epsilon ϵ的概率密度为
p ( ϵ ) = 1 2 π σ exp ( − ϵ 2 2 σ 2 ) p(\epsilon)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\epsilon^{2}}{2 \sigma^{2}}\right) p(ϵ)=2πσ1exp(−2σ2ϵ2)
将 ϵ \epsilon ϵ替换成 y − ( w x + b ) y-(w x+b) y−(wx+b),之后得到的式子,可以将y看成随机变量,即得到了y的概率密度函数
p ( y ) = 1 2 π σ exp ( − ( y − ( w x + b ) ) 2 2 σ 2 ) p(y)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y-(w x+b))^{2}\right.}{2 \sigma^{2}}\right) p(y)=2πσ1exp(−2σ2(y−(wx+b))2)
总结下,上述过程,通过对 ϵ \epsilon ϵ进行建模,进而得到 y y y的建模, y ∼ N ( w x + b , σ 2 ) y \sim N\left({w} x+{b}, \sigma^{2}\right) y∼N(wx+b,σ2)
接下来使用极大似然估计,来估计 w w w和 b b b
L ( w , b ) = ∏ i = 1 m p ( y i ) = ∏ i = 1 m 1 2 π σ exp ( − ( y i − ( w x i + b ) ) 2 2 σ 2 ) ln L ( w , b ) = ∑ i = 1 m ln 1 2 π σ exp ( − ( y i − w x i − b ) 2 2 σ 2 ) = ∑ i = 1 m ln 1 2 π σ + ∑ i = 1 m ln exp ( − ( y i − w x i − b ) 2 2 σ 2 ) = m ln 1 2 π σ − 1 2 σ 2 ∑ i = 1 m ( y i − w x i − b ) 2 \begin{aligned} L(w, b)=& \prod_{i=1}^{m} p\left(y_{i}\right)=\prod_{i=1}^{m} \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-\left(w x_{i}+b\right)\right)^{2}}{2 \sigma^{2}}\right) \\ \ln L(w, b) &=\sum_{i=1}^{m} \ln \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{\left(y_{i}-w x_{i}-b\right)^{2}}{2 \sigma^{2}}\right) \\ &=\sum_{i=1}^{m} \ln \frac{1}{\sqrt{2 \pi} \sigma}+\sum_{i=1}^{m} \ln \exp \left(-\frac{\left(y_{i}-w x_{i}-b\right)^{2}}{2 \sigma^{2}}\right)\\ &=m \ln \frac{1}{\sqrt{2 \pi} \sigma}-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} \end{aligned} L(w,b)=lnL(w,b)i=1∏mp(yi)=i=1∏m2πσ1exp(−2σ2(yi−(wxi+b))2)=i=1∑mln2πσ1exp(−2σ2(yi−wxi−b)2)=i=1∑mln2πσ1+i=1∑mlnexp(−2σ2(yi−wxi−b)2)=mln2πσ1−2σ21i=1∑m(yi−wxi−b)2
其中 m m m和 σ \sigma σ均为常数,所以最大化 ln L ( w , b ) \ln L(w, b) lnL(w,b) 等价于最小化 $ \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2}$
( w ∗ , b ∗ ) = arg max ( w , b ) ln L ( w , b ) = arg min ( w , b ) ∑ i = 1 m ( y i − w x i − b ) 2 \left(w^{*}, b^{*}\right)=\underset{(w, b)}{\arg \max } \ln L(\boldsymbol{w}, b)=\underset{(w, b)}{\arg \min } \sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} (w∗,b∗)=(w,b)argmaxlnL(w,b)=(w,b)argmini=1∑m(yi−wxi−b)2
所以极大似然估计和最小二乘法的目标是相同的
数学概念
n元实值函数
含有 n n n个自变量,值域为实数域 R \mathbb{R} R的函数,称为n元实值函数
(多元函数未加特殊说明均为实值函数)
凸集
设集合 D ⊂ R n D \subset \mathbb{R}^{n} D⊂Rn 为 n n n 维欧式空间中的子集
如果对 D D D 中任意的 n n n 维向量 x ∈ D \boldsymbol{x} \in D x∈D 和 y ∈ D \boldsymbol{y} \in D y∈D 与 任意的 α ∈ [ 0 , 1 ] \alpha \in[0,1] α∈[0,1] , 有
α x + ( 1 − α ) y ∈ D \alpha \boldsymbol{x}+(1-\alpha) \boldsymbol{y} \in D αx+(1−α)y∈D
则称集合 D D D 是凸集
凸集的几何意义
- 若两个点属于此集合, 则这两点连线上的任意一点均属于此集合
- 常见的凸集有空集 ∅ \varnothing ∅ , 整个 n n n 维欧式空间 $\mathbb{R}^{n} $
凸函数
对于区间 [ a , b ] [a,b] [a,b]上定义的函数 f f f,若对区间中任意两点 x 1 , x 2 x_1,x_2 x1,x2均有
f ( x 1 + x 2 2 ) ⩽ f ( x 1 ) + f ( x 2 ) 2 f\left(\frac{x_{1}+x_{2}}{2}\right) \leqslant \frac{f\left(x_{1}\right)+f\left(x_{2}\right)}{2} f(2x1+x2)⩽2f(x1)+f(x2)
则称 f f f为区间 [ a , b ] [a,b] [a,b]上的凸函数
-
U形曲线的函数通常是凸函数
- 例: y = x 2 y=x^2 y=x2
-
(在高等数学定义中称之为凹函数)
梯度
分母布局
∇ f ( x ) = ∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \nabla f(\boldsymbol{x})=\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}=\left[\begin{array}{c} \frac{\partial f(\boldsymbol{x})}{\partial x_{1}} \\ \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \end{array}\right] ∇f(x)=∂x∂f(x)=⎣ ⎡∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)⎦ ⎤
分子布局
∇ f ( x ) = ∂ f ( x ) ∂ x T = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , ⋯ , ∂ f ( x ) ∂ x n ] \nabla f(\boldsymbol{x})=\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}^{\mathrm{T}}}=\left[\frac{\partial f(\boldsymbol{x})}{\partial x_{1}}, \frac{\partial f(\boldsymbol{x})}{\partial x_{2}}, \cdots, \frac{\partial f(\boldsymbol{x})}{\partial x_{n}}\right] ∇f(x)=∂xT∂f(x)=[∂x1∂f(x),∂x2∂f(x),⋯,∂xn∂f(x)]
- 梯度指向的方向是函数值增大速度最快的方向
- 在最优化中习惯采用分母布局
Hessian矩阵
∇ 2 f ( x ) = ∂ 2 f ( x ) ∂ x ∂ x T = [ ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 ⋯ ∂ 2 f ( x ) ∂ x 1 ∂ x n ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 ⋯ ∂ 2 f ( x ) ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 … ∂ 2 f ( x ) ∂ x n 2 ] \nabla^{2} f(\boldsymbol{x})=\frac{\partial^{2} f(\boldsymbol{x})}{\partial \boldsymbol{x} \partial \boldsymbol{x}^{T}}=\left[\begin{array}{cccc} \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{1}^{2}} & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{n} \partial x_{2}} & \ldots & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{n}^{2}} \end{array}\right] ∇2f(x)=∂x∂xT∂2f(x)=⎣ ⎡∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)⋯⋯⋱…∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)⎦ ⎤
- 二阶偏导数均连续, ∂ 2 f ( x ) ∂ x i ∂ x j = ∂ 2 f ( x ) ∂ x j ∂ x i \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{i} \partial x_{j}}=\frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{j} \partial x_{i}} ∂xi∂xj∂2f(x)=∂xj∂xi∂2f(x)
凸函数的判断
对于实数集上的函数
二阶导数
- 在区间上非负,称为凸函数
- 在区间上恒大于0,称为严格凸函数
闭式解/解析解
可以通过具体的表达式解出待解参数
机器学习算法很少有闭式解,线性回归是一个特例
标量-向量的矩阵微分公式
设 x ∈ R n × 1 , f : R n → R \boldsymbol{x} \in \mathbb{R}^{n \times 1}, f: \mathbb{R}^{n} \rightarrow \mathbb{R} x∈Rn×1,f:Rn→R 为关于 x \boldsymbol{x} x 的实值标量函数, 则
∂ f ( x ) ∂ x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] , ∂ f ( x ) ∂ x T = ( ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋯ ∂ f ( x ) ∂ x n ) \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}=\left[\begin{array}{c} \frac{\partial f(\boldsymbol{x})}{\partial x_{1}} \\ \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} \\ \vdots \\ \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \end{array}\right], \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}^{\mathrm{T}}}=\left(\begin{array}{llll} \frac{\partial f(\boldsymbol{x})}{\partial x_{1}} & \frac{\partial f(\boldsymbol{x})}{\partial x_{2}} & \cdots & \frac{\partial f(\boldsymbol{x})}{\partial x_{n}} \end{array}\right) ∂x∂f(x)=⎣ ⎡∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)⎦ ⎤,∂xT∂f(x)=(∂x1∂f(x)∂x2∂f(x)⋯∂xn∂f(x))
左侧为分母布局,右侧为分子布局
矩阵分析/矩阵微分
对向量/矩阵进行求导,求一阶偏导之后按照不同的规则,将得到结果进行排列
单变量线性回归
求解过程
第一步: E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数
证明 E ( w , b ) = ∑ i = 1 m ( y i − w x i − b ) 2 E_{(w, b)}=\sum_{i=1}^{m}\left(y_{i}-w x_{i}-b\right)^{2} E(w,b)=∑i=1m(yi−wxi−b)2 的Hessian (海塞) 矩阵是半正定的
∇ 2 E ( w , b ) = [ ∂ 2 E ( w , b ) ∂ w 2 ∂ 2 E ( w , b ) ∂ w ∂ b ∂ ( w , b ) ∂ b ∂ w ∂ 2 E ( w , b ) ∂ b 2 ] = [ 2 ∑ i = 1 m x i 2 2 ∑ i = 1 m x i 2 ∑ i = 1 m x i 2 m ] \nabla^{2} E_{(w, b)}=\left[\begin{array}{ll} \frac{\partial^{2} E_{(w, b)}}{\partial w^{2}} & \frac{\partial^{2} E_{(w, b)}}{\partial w \partial b} \\ \frac{\partial_{(w, b)}}{\partial b \partial w} & \frac{\partial^{2} E_{(w, b)}}{\partial b^{2}} \end{array}\right] =\left[\begin{array}{cc} 2 \sum_{i=1}^{m} x_{i}^{2} & 2 \sum_{i=1}^{m} x_{i} \\ 2 \sum_{i=1}^{m} x_{i} & 2 m \end{array}\right] ∇2E(w,b)=[∂w2∂2E(w,b)∂b∂w∂(w,b)∂w∂b∂2E(w,b)∂b2∂2E(w,b)]=[2∑i=1mxi22∑i=1mxi2∑i=1mxi2m]
利用半正定矩阵的判别定理之一:若实对称矩阵的所有顺序主子式均为非负,则该矩阵为半正定矩阵
∣ 2 ∑ i = 1 m x i 2 ∣ > 0 ∣ 2 ∑ i = 1 m x i 2 2 ∑ i = 1 m x i 2 ∑ i = 1 m x i 2 m ∣ = 2 ∑ i = 1 m x i 2 ⋅ 2 m − 2 ∑ i = 1 m x i ⋅ 2 ∑ i = 1 m x i = 4 m ∑ i = 1 m x i 2 − 4 ( ∑ i = 1 m x i ) 2 \begin{array}{l} \left|2 \sum_{i=1}^{m} x_{i}^{2}\right|>0\\ \left|\begin{array}{cc} 2 \sum_{i=1}^{m} x_{i}^{2} & 2 \sum_{i=1}^{m} x_{i} \\ 2 \sum_{i=1}^{m} x_{i} & 2 m \end{array}\right|=2 \sum_{i=1}^{m} x_{i}^{2} \cdot 2 m-2 \sum_{i=1}^{m} x_{i} \cdot 2 \sum_{i=1}^{m} x_{i}\\ =4 m \sum_{i=1}^{m} x_{i}^{2}-4\left(\sum_{i=1}^{m} x_{i}\right)^{2} \end{array} ∣ ∣2∑i=1mxi2∣ ∣>0∣ ∣2∑i=1mxi22∑i=1mxi2∑i=1mxi2m∣ ∣=2∑i=1mxi2⋅2m−2∑i=1mxi⋅2∑i=1mxi=4m∑i=1mxi2−4(∑i=1mxi)2
4 m ∑ i = 1 m x i 2 − 4 ( ∑ i = 1 m x i ) 2 = 4 m ∑ i = 1 m x i 2 − 4 ⋅ m ⋅ 1 m ⋅ ( ∑ i = 1 m x i ) 2 = 4 m ∑ i = 1 m x i 2 − 4 m ⋅ x ˉ ⋅ ∑ i = 1 m x i = 4 m ( ∑ i = 1 m x i 2 − ∑ i = 1 m x i x ˉ ) = 4 m ∑ i = 1 m ( x i 2 − x i x ˉ ) 由于 ∑ i = 1 m x i x ˉ = x ˉ ∑ i = 1 m x i = x ˉ ⋅ m ⋅ 1 m ⋅ ∑ i = 1 m x i = m x ˉ 2 = ∑ i = 1 m x ˉ 2 = 4 m ∑ i = 1 m ( x i 2 − x i x ˉ − x i x ˉ + x i x ˉ ) = 4 m ∑ i = 1 m ( x i 2 − x i x ˉ − x i x ˉ + x ˉ 2 ) = 4 m ∑ i = 1 m ( x i − x ˉ ) 2 \begin{array}{c} \quad 4 m \sum_{i=1}^{m} x_{i}^{2}-4\left(\sum_{i=1}^{m} x_{i}\right)^{2} \\ \\ =4 m \sum_{i=1}^{m} x_{i}^{2}-4 \cdot m \cdot \frac{1}{m} \cdot\left(\sum_{i=1}^{m} x_{i}\right)^{2} \\ \\ =4 m \sum_{i=1}^{m} x_{i}^{2}-4 m \cdot \bar{x} \cdot \sum_{i=1}^{m} x_{i}\\ \\ =4 m\left(\sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m} x_{i} \bar{x}\right)\\ \\ =4 m \sum_{i=1}^{m}\left(x_{i}^{2}-x_{i} \bar{x}\right) \\ \\ \text { 由于 } \sum_{i=1}^{m} x_{i} \bar{x}=\bar{x} \sum_{i=1}^{m} x_{i}=\bar{x} \cdot m \cdot \frac{1}{m} \cdot \sum_{i=1}^{m} x_{i}=m \bar{x}^{2}=\sum_{i=1}^{m} \bar{x}^{2} \\ \\ =4 m \sum_{i=1}^{m}\left(x_{i}^{2}-x_{i} \bar{x}-x_{i} \bar{x}+x_{i} \bar{x}\right)=4 m \sum_{i=1}^{m}\left(x_{i}^{2}-x_{i} \bar{x}-x_{i} \bar{x}+\bar{x}^{2}\right)=4 m \sum_{i=1}^{m}\left(x_{i}-\bar{x}\right)^{2} \end{array} 4m∑i=1mxi2−4(∑i=1mxi)2=4m∑i=1mxi2−4⋅m⋅m1⋅(∑i=1mxi)2=4m∑i=1mxi2−4m⋅xˉ⋅∑i=1mxi=4m(∑i=1mxi2−∑i=1mxixˉ)=4m∑i=1m(xi2−xixˉ) 由于 ∑i=1mxixˉ=xˉ∑i=1mxi=xˉ⋅m⋅m1⋅∑i=1mxi=mxˉ2=∑i=1mxˉ2=4m∑i=1m(xi2−xixˉ−xixˉ+xixˉ)=4m∑i=1m(xi2−xixˉ−xixˉ+xˉ2)=4m∑i=1m(xi−xˉ)2
所以 4 m ∑ i = 1 m ( x i − x ˉ ) 2 ⩾ 0 4 m \sum_{i=1}^{m}\left(x_{i}-\bar{x}\right)^{2} \geqslant 0 4m∑i=1m(xi−xˉ)2⩾0 , Hessian (海塞) 矩阵 ∇ 2 E ( w , b ) \nabla^{2} E_{(w, b)} ∇2E(w,b) 的所有顺序主子式均非负, 该矩阵为半正定矩阵, 进而 E ( w , b ) E_{(w, b)} E(w,b) 是关于 w w w 和 b b b 的凸函数得证。
第二步:用凸函数求最值的思路,令 w w w和 b b b的导数均为0,得到w和b的最优解的闭式(closed-form)解, w ∗ w^* w∗和 b ∗ b^* b∗
∂ E ( w , b ) ∂ w = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) ∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) \begin{array}{l} \frac{\partial E_{(w, b)}}{\partial w}=2\left(w \sum_{i=1}^{m} x_{i}^{2}-\sum_{i=1}^{m}\left(y_{i}-b\right) x_{i}\right) \\ \frac{\partial E_{(w, b)}}{\partial b}=2\left(m b-\sum_{i=1}^{m}\left(y_{i}-w x_{i}\right)\right) \end{array} ∂w∂E(w,b)=2(w∑i=1mxi2−∑i=1m(yi−b)xi)∂b∂E(w,b)=2(mb−∑i=1m(yi−wxi))
w = ∑ i = 1 m y i ( x i − x ˉ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 b = 1 m ∑ i = 1 m ( y i − w x i ) w=\frac{\sum_{i=1}^{m} y_{i}\left(x_{i}-\bar{x}\right)}{\sum_{i=1}^{m} x_{i}^{2}-\frac{1}{m}\left(\sum_{i=1}^{m} x_{i}\right)^{2}}\\ b=\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-w x_{i}\right) w=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−xˉ)b=m1i=1∑m(yi−wxi)
若令 x = ( x 1 ; x 2 ; … ; x m ) , x d = ( x 1 − x ˉ ; x 2 − x ˉ ; … ; x m − x ˉ ) \boldsymbol{x}=\left(x_{1} ; x_{2} ; \ldots ; x_{m}\right), \boldsymbol{x}_{d}=\left(x_{1}-\bar{x} ; x_{2}-\bar{x} ; \ldots ; x_{m}-\bar{x}\right) x=(x1;x2;…;xm),xd=(x1−xˉ;x2−xˉ;…;xm−xˉ) 为去均值后的 x \boldsymbol{x} x ;
y = ( y 1 ; y 2 ; … ; y m ) , y d = ( y 1 − y ˉ ; y 2 − y ˉ ; … ; y m − y ˉ ) \boldsymbol{y}=\left(y_{1} ; y_{2} ; \ldots ; y_{m}\right), \boldsymbol{y}_{d}= \left(y_{1}-\bar{y} ; y_{2}-\bar{y} ; \ldots ; y_{m}-\bar{y}\right) y=(y1;y2;…;ym),yd=(y1−yˉ;y2−yˉ;…;ym−yˉ) 为去均值后的 y \boldsymbol{y} y
化简之后,可以使用矩阵乘法得到的 w w w结果
w = x d T y d x d T x d w=\frac{\boldsymbol{x}_{d}^{\mathrm{T}} \boldsymbol{y}_{d}}{\boldsymbol{x}_{d}^{\mathrm{T}} \boldsymbol{x}_{d}} w=xdTxdxdTyd
多元线性回归
为方便式子进行化简
将 b b b吸收入 w w w中得到 w ^ = ( w ; b ) \hat{\boldsymbol{w}}=(\boldsymbol{w} ; b) w^=(w;b)
同时对 x x x进行整理
X = ( x 11 x 12 … x 1 d 1 x 21 x 22 … x 2 d 1 ⋮ ⋮ ⋱ ⋮ ⋮ x m 1 x m 2 … x m d 1 ) = ( x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ) \mathbf{X}=\left(\begin{array}{ccccc} x_{11} & x_{12} & \ldots & x_{1 d} & 1 \\ x_{21} & x_{22} & \ldots & x_{2 d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m 1} & x_{m 2} & \ldots & x_{m d} & 1 \end{array}\right)=\left(\begin{array}{cc} x_{1}^{\mathrm{T}} & 1 \\ x_{2}^{\mathrm{T}} & 1 \\ \vdots & \vdots \\ x_{m}^{\mathrm{T}} & 1 \end{array}\right) X=⎝ ⎛x11x21⋮xm1x12x22⋮xm2……⋱…x1dx2d⋮xmd11⋮1⎠ ⎞=⎝ ⎛x1Tx2T⋮xmT11⋮1⎠ ⎞
同时将标记写成向量形式 y = ( y 1 ; y 2 ; … ; y m ) \boldsymbol{y}=\left(y_{1} ; y_{2} ; \ldots ; y_{m}\right) y=(y1;y2;…;ym)
最终求解的目标写成
w ^ ∗ = arg min w ^ ( y − X w ^ ) T ( y − X w ^ ) \hat{\boldsymbol{w}}^{*}=\underset{\hat{\boldsymbol{w}}}{\arg \min }(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}}) w^∗=w^argmin(y−Xw^)T(y−Xw^)
该式子的化简过程
具体如下:
E w ^ = ∑ i = 1 m ( y i − w ^ T x ^ i ) 2 = ( y 1 − w ^ T x ^ 1 ) 2 + ( y 2 − w ^ T x ^ 2 ) 2 + … + ( y m − w ^ T x ^ m ) 2 E_{\hat{\boldsymbol{w}}}=\sum_{i=1}^{m}\left(y_{i}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{i}\right)^{2}=\left(y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1}\right)^{2}+\left(y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2}\right)^{2}+\ldots+\left(y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m}\right)^{2} Ew^=i=1∑m(yi−w^Tx^i)2=(y1−w^Tx^1)2+(y2−w^Tx^2)2+…+(ym−w^Tx^m)2
E w ^ = ( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋯ y m − w ^ T x ^ m ) ( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋮ y m − w ^ T x ^ m ) E_{\hat{\boldsymbol{w}}}=\left(\begin{array}{cccc} y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} & y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} & \cdots & y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right)\left(\begin{array}{c} y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} \\ y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} \\ \vdots \\ y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right) Ew^=(y1−w^Tx^1y2−w^Tx^2⋯ym−w^Tx^m)⎝ ⎛y1−w^Tx^1y2−w^Tx^2⋮ym−w^Tx^m⎠ ⎞
( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋮ y m − w ^ T x ^ m ) = ( y 1 y 2 ⋮ y m ) − ( w ^ T x ^ 1 w ^ T x ^ 2 ⋮ w ^ T x ^ m ) = ( y 1 y 2 ⋮ y m ) − ( x ^ 1 T w ^ x ^ 2 T w ^ ⋮ x ^ m T w ^ ) \left(\begin{array}{c} y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} \\ y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} \\ \vdots \\ y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right)=\left(\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{array}\right)-\left(\begin{array}{c} \hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} \\ \hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} \\ \vdots \\ \hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right)=\left(\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{array}\right)-\left(\begin{array}{c} \hat{\boldsymbol{x}}_{1}^{\mathrm{T}} \hat{\boldsymbol{w}} \\ \hat{\boldsymbol{x}}_{2}^{\mathrm{T}} \hat{\boldsymbol{w}} \\ \vdots \\ \hat{\boldsymbol{x}}_{m}^{\mathrm{T}} \hat{\boldsymbol{w}} \end{array}\right) ⎝ ⎛y1−w^Tx^1y2−w^Tx^2⋮ym−w^Tx^m⎠ ⎞=⎝ ⎛y1y2⋮ym⎠ ⎞−⎝ ⎛w^Tx^1w^Tx^2⋮w^Tx^m⎠ ⎞=⎝ ⎛y1y2⋮ym⎠ ⎞−⎝ ⎛x^1Tw^x^2Tw^⋮x^mTw^⎠ ⎞
y = ( y 1 y 2 ⋮ y m ) , ( x ^ 1 T w ^ x ^ 2 T w ^ ⋮ x ^ m T w ^ ) = ( x ^ 1 T x ^ 2 T ⋮ x ^ m T ) ⋅ w ^ = ( x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ) ⋅ w ^ = X ⋅ w ^ \boldsymbol{y}=\left(\begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{array}\right), \quad\left(\begin{array}{c} \hat{\boldsymbol{x}}_{1}^{\mathrm{T}} \hat{\boldsymbol{w}} \\ \hat{\boldsymbol{x}}_{2}^{\mathrm{T}} \hat{\boldsymbol{w}} \\ \vdots \\ \hat{\boldsymbol{x}}_{m}^{\mathrm{T}} \hat{\boldsymbol{w}} \end{array}\right)=\left(\begin{array}{c} \hat{\boldsymbol{x}}_{1}^{\mathrm{T}} \\ \hat{\boldsymbol{x}}_{2}^{\mathrm{T}} \\ \vdots \\ \hat{\boldsymbol{x}}_{m}^{\mathrm{T}} \end{array}\right) \cdot \hat{\boldsymbol{w}}=\left(\begin{array}{cc} \boldsymbol{x}_{1}^{\mathrm{T}} & 1 \\ \boldsymbol{x}_{2}^{\mathrm{T}} & 1 \\ \vdots & \vdots \\ \boldsymbol{x}_{m}^{\mathrm{T}} & 1 \end{array}\right) \cdot \hat{\boldsymbol{w}}=\mathbf{X} \cdot \hat{\boldsymbol{w}} y=⎝ ⎛y1y2⋮ym⎠ ⎞,⎝ ⎛x^1Tw^x^2Tw^⋮x^mTw^⎠ ⎞=⎝ ⎛x^1Tx^2T⋮x^mT⎠ ⎞⋅w^=⎝ ⎛x1Tx2T⋮xmT11⋮1⎠ ⎞⋅w^=X⋅w^
( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋮ y m − w ^ T x ^ m ) = y − X w ^ \left(\begin{array}{c} y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} \\ y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} \\ \vdots \\ y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right)=\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}} ⎝ ⎛y1−w^Tx^1y2−w^Tx^2⋮ym−w^Tx^m⎠ ⎞=y−Xw^
E w ^ = ( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋯ y m − w ^ T x ^ m ) ( y 1 − w ^ T x ^ 1 y 2 − w ^ T x ^ 2 ⋮ y m − w ^ T x ^ m ) E w ^ = ( y − X w ^ ) T ( y − X w ^ ) \begin{array}{l} E_{\hat{\boldsymbol{w}}}=\left(\begin{array}{cccc} y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} & y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} & \cdots & y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right)\left(\begin{array}{c} y_{1}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{1} \\ y_{2}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{2} \\ \vdots \\ y_{m}-\hat{\boldsymbol{w}}^{\mathrm{T}} \hat{\boldsymbol{x}}_{m} \end{array}\right)\\ E_{\hat{\boldsymbol{w}}}=(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}}) \end{array} Ew^=(y1−w^Tx^1y2−w^Tx^2⋯ym−w^Tx^m)⎝ ⎛y1−w^Tx^1y2−w^Tx^2⋮ym−w^Tx^m⎠ ⎞Ew^=(y−Xw^)T(y−Xw^)
求解 w ^ \hat{w} w^
- 证明 E w ^ = ( y − X w ^ ) T ( y − X w ^ ) E_{\hat{\boldsymbol{w}}}=(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}}) Ew^=(y−Xw^)T(y−Xw^) 是关于 $\hat{\boldsymbol{w}} $ 的凸函数
- 用凸函数求最值的思路求解出 w ^ \hat{\boldsymbol{w}} w^
求 $E_{\hat{w}} $ 的Hessian (海塞) 矩阵 ∇ 2 E w ^ \nabla^{2} E_{\hat{\boldsymbol{w}}} ∇2Ew^ , 然后判断其正定性:
∂ E w ^ ∂ w ^ = ∂ ∂ w ^ [ ( y − X w ^ ) T ( y − X w ^ ) ] = ∂ ∂ w ^ [ ( y T − w ^ T X T ) ( y − X w ^ ) ] = ∂ ∂ w ^ [ y T y − y T X w ^ − w ^ T X T y + w ^ T X T X w ^ ] = ∂ ∂ w ^ [ − y T X w ^ − w ^ T X T y + w ^ T X T X w ^ ] = − ∂ y T X w ^ ∂ w ^ − ∂ w ^ T X T y ∂ w ^ + ∂ w ^ T X T X w ^ ∂ w ^ \begin{aligned} \frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}} &=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left[(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})^{\mathrm{T}}(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})\right] \\ &=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left[\left(\boldsymbol{y}^{\mathrm{T}}-\hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}}\right)(\boldsymbol{y}-\mathbf{X} \hat{\boldsymbol{w}})\right] \\ &=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left[\boldsymbol{y}^{\mathrm{T}} \boldsymbol{y}-\boldsymbol{y}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}-\hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \boldsymbol{y}+\hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}\right] \\ &=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left[-\boldsymbol{y}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}-\hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \boldsymbol{y}+\hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}\right] \\ &=-\frac{\partial \boldsymbol{y}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}}{\partial \hat{\boldsymbol{w}}}-\frac{\partial \hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \boldsymbol{y}}{\partial \hat{\boldsymbol{w}}}+\frac{\partial \hat{\boldsymbol{w}}^{\mathrm{T}} \mathbf{X}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}}{\partial \hat{\boldsymbol{w}}} \end{aligned} ∂w^∂Ew^=∂w^∂[(y−Xw^)T(y−Xw^)]=∂w^∂[(yT−w^TXT)(y−Xw^)]=∂w^∂[yTy−yTXw^−w^TXTy+w^TXTXw^]=∂w^∂[−yTXw^−w^TXTy+w^TXTXw^]=−∂w^∂yTXw^−∂w^∂w^TXTy+∂w^∂w^TXTXw^
利用矩阵微分公式
∂ x T a ∂ x = ∂ a T x ∂ x = a \frac{\partial x^{\mathrm{T}} \boldsymbol{a}}{\partial \boldsymbol{x}}=\frac{\partial \boldsymbol{a}^{\mathrm{T}} \boldsymbol{x}}{\partial \boldsymbol{x}}=\boldsymbol{a} ∂x∂xTa=∂x∂aTx=a
∂ x T A x ∂ x = ( A + A T ) x \frac{\partial \boldsymbol{x}^{\mathrm{T}} \mathbf{A} \boldsymbol{x}}{\partial \boldsymbol{x}}=\left(\mathbf{A}+\mathbf{A}^{\mathrm{T}}\right) \boldsymbol{x} ∂x∂xTAx=(A+AT)x
∂ A x x = A T \frac{\partial \mathbf{A} \boldsymbol{x}}{\boldsymbol{x}}=\mathbf{A}^{\mathrm{T}} x∂Ax=AT
可以得到
∂ E w ^ ∂ w ^ = − X T y − X T y + ( X T X + X T X ) w ^ = 2 X T ( X w ^ − y ) \begin{aligned} \frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}} &=-\mathbf{X}^{T} \boldsymbol{y}-\mathbf{X}^{T} \boldsymbol{y}+\left(\mathbf{X}^{T} \mathbf{X}+\mathbf{X}^{T} \mathbf{X}\right) \hat{\boldsymbol{w}} \\ &=2 \mathbf{X}^{\mathrm{T}}(\mathbf{X} \hat{\boldsymbol{w}}-\boldsymbol{y}) \end{aligned} ∂w^∂Ew^=−XTy−XTy+(XTX+XTX)w^=2XT(Xw^−y)
∇ 2 E w ^ = ∂ ∂ w ^ ( ∂ E w ^ ∂ w ^ ) = ∂ ∂ w ^ [ 2 X T ( X w ^ − y ) ] = ∂ ∂ w ^ ( 2 X T X w ^ − 2 X T y ) = 2 X T X \begin{aligned} \nabla^{2} E_{\hat{\boldsymbol{w}}} &=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left(\frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}}\right) \\ &=\frac{\partial}{\partial \hat{\boldsymbol{w}}} {\left[2 \mathbf{X}^{\mathrm{T}}(\mathbf{X} \hat{\boldsymbol{w}}-\boldsymbol{y})\right]} \\ &=\frac{\partial}{\partial \hat{\boldsymbol{w}}}\left(2 \mathbf{X}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}-2 \mathbf{X}^{\mathrm{T}} \boldsymbol{y}\right)\\ &=2 \mathbf{X}^{\mathrm{T}} \mathbf{X} \end{aligned} ∇2Ew^=∂w^∂(∂w^∂Ew^)=∂w^∂[2XT(Xw^−y)]=∂w^∂(2XTXw^−2XTy)=2XTX
对$ \mathbf{X}^{\mathrm{T}} \mathbf{X}$分情况讨论
1)为满秩矩阵或者正定矩阵时
∂ E w ^ ∂ w ^ = 2 X T ( X w ^ − y ) = 0 2 X T X w ^ − 2 X T y = 0 2 X T X w ^ = 2 X T y w ^ = ( X T X ) − 1 X T y \begin{array}{c} \frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial \hat{\boldsymbol{w}}} =2 \mathbf{X}^{\mathrm{T}}(\mathbf{X} \hat{\boldsymbol{w}}-\boldsymbol{y})=0 \\ 2 \mathbf{X}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}-2 \mathbf{X}^{\mathrm{T}} \boldsymbol{y}=0 \\ 2 \mathbf{X}^{\mathrm{T}} \mathbf{X} \hat{\boldsymbol{w}}=2 \mathbf{X}^{\mathrm{T}} \boldsymbol{y} \\ \hat{\boldsymbol{w}}=\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \boldsymbol{y} \end{array} ∂w^∂Ew^=2XT(Xw^−y)=02XTXw^−2XTy=02XTXw^=2XTyw^=(XTX)−1XTy
得到的线性回归模型为 f ( x ^ i ) = x ^ i T ( X T X ) − 1 X T y f\left(\hat{\boldsymbol{x}}_{i}\right)=\hat{\boldsymbol{x}}_{i}^{\mathrm{T}}\left(\mathbf{X}^{\mathrm{T}} \mathbf{X}\right)^{-1} \mathbf{X}^{\mathrm{T}} \boldsymbol{y} f(x^i)=x^iT(XTX)−1XTy
2)不为满秩矩阵时
会有多个 w ^ \hat{w} w^的解,此时选择哪儿个解,由学习算法的归纳偏好决定,常见的做法是引入正则化
广义线性模型
y = g − 1 ( w T x + b ) y=g^{-1}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b\right) y=g−1(wTx+b)
- $ g(·)$
- 为单调可微函数,同时连续且充分光滑
- 称为联系函数
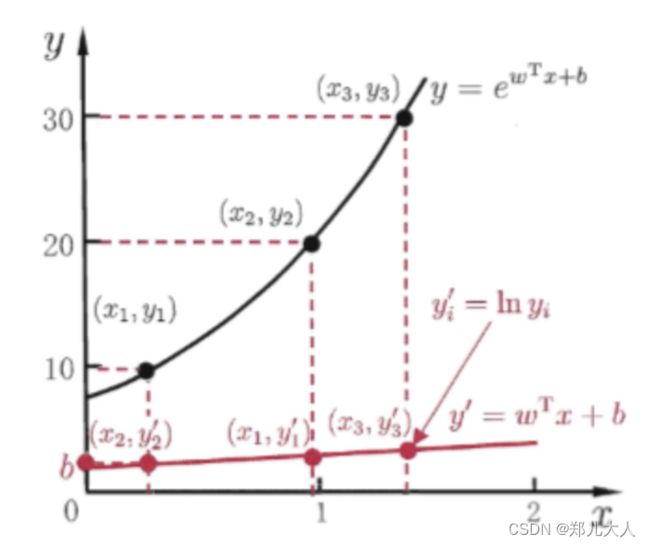
对数线性回归
ln y = w T x + b \ln y=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b lny=wTx+b
形式为线性回归,本质是让 y y y接近 e w T x + b e^{\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b} ewTx+b
求取输入空间到输出空间的非线性映射