基于人工蜂群算法的线性规划求解matlab程序

基于人工蜂群算法的线性规划求解matlab程序

1 人工蜂群算法概述
2005年D. Karaboga教授仿照蜜蜂集群采蜜生物行为，提出了人工蜂群仿生算法，可以有效解决有关函数优化等相关难题。ABC算法仿照蜜蜂蜂群中不同蜂种相互协作，蜂群间进行角色转换的工作方式完成信息之间的传递与分享，不断寻优找到最佳的蜜源。ABC算法结构简单操作容易、参数个数少、且待求解的问题的特殊信息不需要被知晓，只需要计算待求解问题的可行性解的适应度值并通过贪婪算法挑选出较优的食物源。单个蜜蜂在局部范围内搜索优质的解，最终整个群体便会向全局最优解趋近，优化搜索的效率较高，因此近年来广大研究学者将人工蜂群算法应用到各个领域之中。

自然界中蜜蜂与熊猫、仓鼠等独居动物不同，由于单个蜜蜂个体的行为特征十分简单，不能完成复杂的活动，因此蜜蜂常以群居的方式共同生活在一起，蜂群中的各个蜂种协同合作，各司其职，彼此间进行信息交互可以使蜂群具有复杂的行为模式，可以保证当蜂群处于恶劣的环境中时，依旧可以井然有序地搜索到蜜源的位置从而采集到花蜜。

蜜蜂属于高级的社会性昆虫，蜂群中不同的蜜蜂个体协调合作完成采蜜等社会性行为。当蜜蜂进行采蜜时，一部分工蜂转化为侦查蜂外出搜索食物源，只要发现高品质的蜜源，这些侦查蜂便会转变为采蜜蜂，采蜜后返回蜂巢大本营，通过跳“8”字型舞蹈或者圆圈舞将信息传达给同伴，这种舞蹈称为“摇摆舞”。通过跳摇摆舞可以隐晦地表现出蜜源的一些相关信息，舞蹈的持续时间越长表明该位置的食物源品质越高，摇摆舞与蜂巢之间和与太阳之间的方位关系决定了蜜源的方向。同伴们通过观察多个采蜜蜂带回来的信息并挑选自己认为最好的蜜源，转化为跟随蜂并开始跟随采蜜蜂一起前往蜜源位置进行采蜜，于是整个蜂群便会逐步向最好品质的蜜源位置处前进。以这种方式进行采蜜，蜜蜂之间角色进行相互转换，有序协调合作，可以使蜂群快速地适应环境的改变，当已被收集的蜜源品质逐渐降低或发现有更高质量的蜜源时，侦查蜂可以高效快速地向整个蜂群传达出最及时的蜜源信息，引导整个蜂群高效的采集到花粉数量最多的食物源。
蜜蜂种群采蜜的模型中包含了3种主要的组成部分：食物源、雇佣蜂和非雇佣蜂。

（1）食物源 也称为蜜源，是人工蜂群算法中的研究主体。蜜源的质量由蜜源距离蜂巢的远近程度、蜜源中的花粉数量以及对其进行采蜜的难易水平等多方面共同决定的。在优化问题中食物源也有相应的适应度函数可以对其进行评价。

（2）雇佣蜂 即为引领蜂、采蜜蜂。与食物源位置相对应，雇佣蜂的数量与食物源的数量一致。雇佣蜂的职责是在发现食物源后返回蜂巢，以跳舞的方式将食物源的信息进行分享。

（3）非雇佣蜂 包括跟随蜂和侦查蜂两类蜂种。在蜂巢周边随机检索蜜源的是侦查蜂；跟随蜂留守在蜂巢内通过接收雇佣蜂传递回来的信息寻找蜜源。在蜜蜂个体在进行采蜜过程时，包含了两种行为：招募更多蜜蜂到搜索的蜜源处，放弃经过搜索依旧没有更新的蜜源。为更好的理解两种行为，参照图3-1进行具体的说明。

2 线性规划算例
2.1算例

2.2算例答案

3 人工蜂群优化算法求解结果

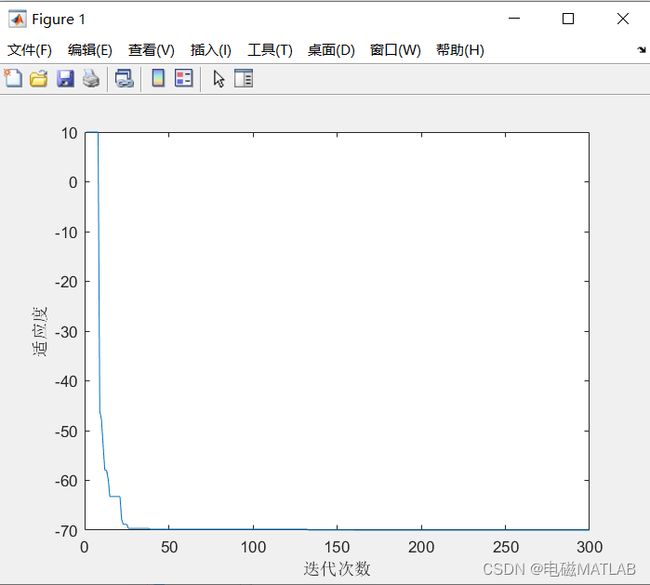
1）迭代曲线

2）求解答案

4 matlab程序
1）主函数

close all
clc
clear
%%
NP=20; %/* The number of colony size (employed bees+onlooker bees)*/f蜂群大小
FoodNumber=NP/2; %/*The number of food sources equals the half of the colony size*/
limit=100; %/*A food source which could not be improved through "limit" trials is abandoned by its employed bee*/
maxCycle=300; %/*The number of cycles for foraging {a stopping criteria}*/
%/* Problem specific variables*/
objfun='Sphere'; %cost function to be optimized29 / 成本函数有待优化 
D=3; %/*The number of parameters of the problem to be optimized*/要优化的问题的参数数量
ub=ones(1,D)*15; %/*lower bounds of the parameters. */参数的下限
lb=ones(1,D)*0;%/*upper bound of the parameters.*/
runtime=1;%/*Algorithm can be run many times in order to see its robustness*/
GlobalMins=zeros(1,runtime);
for r=1:runtime  
% /*All food sources are initialized */
%/*Variables are initialized in the range [lb,ub]. If each parameter has different range, 
%use arrays lb[j], ub[j] instead of lb and ub */
Range = repmat((ub-lb),[FoodNumber 1]);
Lower = repmat(lb, [FoodNumber 1]);
Foods = rand(FoodNumber,D) .* Range + Lower;
ObjVal=feval(objfun,Foods);
Fitness=calculateFitness(ObjVal);
%reset trial counters
trial=zeros(1,FoodNumber);
%/*The best food source is memorized*/
BestInd=find(ObjVal==min(ObjVal));
BestInd=BestInd(end);
GlobalMin=ObjVal(BestInd);
GlobalParams=Foods(BestInd,:);
iter=1;
while ((iter <= maxCycle))
%% %%%%%%% EMPLOYED BEE PHASE %%%%%%%%%%%%%%%%%%%%%%%%
    for i=1:(FoodNumber)        
        %/*The parameter to be changed is determined randomly*/
        Param2Change=fix(rand*D)+1;        
        %/*A randomly chosen solution is used in producing a mutant solution of the solution i*/
        neighbour=fix(rand*(FoodNumber))+1;       
        %/*Randomly selected solution must be different from the solution i*/        
            while(neighbour==i)
                neighbour=fix(rand*(FoodNumber))+1;
            end;        
       sol=Foods(i,:);
       %  /*v_{ij}=x_{ij}+\phi_{ij}*(x_{kj}-x_{ij}) */
       sol(Param2Change)=Foods(i,Param2Change)+(Foods(i,Param2Change)-Foods(neighbour,Param2Change))*(rand-0.5)*2;        
       %  /*if generated parameter value is out of boundaries, it is shifted onto the boundaries*/
        ind=find(solub);
        sol(ind)=ub(ind);       
        %evaluate new solution
        ObjValSol=feval(objfun,sol);
        FitnessSol=calculateFitness(ObjValSol);        
       % /*a greedy selection is applied between the current solution i and its mutant*/
       if (FitnessSol>Fitness(i)) %/*If the mutant solution is better than the current solution i, replace the solution with the mutant and reset the trial counter of solution i*/
            Foods(i,:)=sol;
            Fitness(i)=FitnessSol;
            ObjVal(i)=ObjValSol;
            trial(i)=0;
        else
            trial(i)=trial(i)+1; %/*if the solution i can not be improved, increase its trial counter*/
       end;
 end;  
%% %%%%%%%%%%%%%%%%%%%%%% CalculateProbabilities %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
prob=(0.9.*Fitness./max(Fitness))+0.1;  
%% %%%%%%%%%%%%%%%%%%%%%% ONLOOKER BEE PHASE %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
i=1;
t=0;
while(tub);
        sol(ind)=ub(ind);        
        %evaluate new solution
        ObjValSol=feval(objfun,sol);
        FitnessSol=calculateFitness(ObjValSol);        
       % /*a greedy selection is applied between the current solution i and its mutant*/
       if (FitnessSol>Fitness(i)) %/*If the mutant solution is better than the current solution i, replace the solution with the mutant and reset the trial counter of solution i*/
            Foods(i,:)=sol;
            Fitness(i)=FitnessSol;
            ObjVal(i)=ObjValSol;
            trial(i)=0;
        else
            trial(i)=trial(i)+1; %/*if the solution i can not be improved, increase its trial counter*/
       end;
    end;    
    i=i+1;
    if (i==(FoodNumber)+1) 
        i=1;
    end;   
end; 
%/*The best food source is memorized*/
         ind=find(ObjVal==min(ObjVal));
         ind=ind(end);
         if (ObjVal(ind)limit)
    trial(ind)=0;
    sol=(ub-lb).*rand(1,D)+lb;
    ObjValSol=feval(objfun,sol);
    FitnessSol=calculateFitness(ObjValSol);
    Foods(ind,:)=sol;
    Fitness(ind)=FitnessSol;
    ObjVal(ind)=ObjValSol;
end;
BestCost(iter)=GlobalMin;
fprintf('iter=%d,ObjVal=%g\n',iter,GlobalMin);
       plot(BestCost(1:iter));
    xlabel('迭代次数');
    ylabel('适应度');
    drawnow 
iter=iter+1;
end % End of ABC
GlobalMins(r)=GlobalMin;
end %end of runs
%% 
disp('输出结果')
disp('最优变量')
sol
disp('最优值')
GlobalMin
。。。。。略

5 matlab完整程序链接
https://mp.weixin.qq.com/s?__biz=Mzg4MTc1MjE2Mg==&mid=2247484473&idx=1&sn=0073195207c3deb103a43372969e083b&chksm=cf606534f817ec224071d71b2b2d78394a94cf4b60296cdf74364f8b6b2c721e4ea02d6bbd68&token=858541086&lang=zh_CN#rd