几何向量:空间三角形内心
之前计算过外心了,这次我们计算一下空间三角形内心(内切圆的圆心)。
问:已知世界空间中任意三角形和顶点坐标,求其内心坐标。如下:
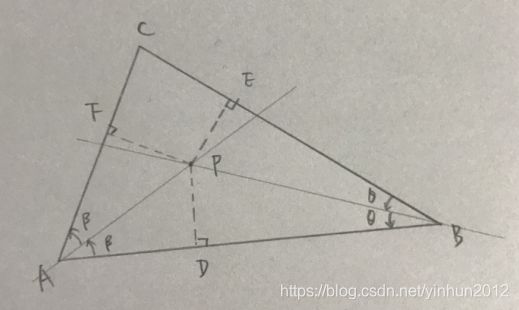
一般平面三角形内心求法:任意两角的平分线相交点即为内心,如图:
这也好理解:△ABC任意两角角度平分后交于P点,做垂线PD、PE、PF,可以组成四个直角三角形,则垂线PD、PE、PF的长度相同,所以交点P即为内心。
那么求空间三角形内心的关键:求空间角平分线,例如求∠BAC平分线AP,如下:
我们得到单位平分线AG的表达式。
接下来就是求△ABC平分线的交点P(x,y,z),也就是内心:
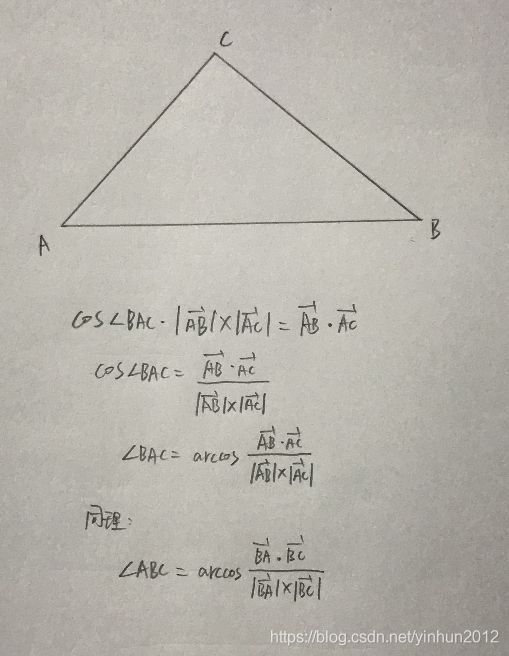
主要是通过直角三角形性质,求得r2或者r1的长度,即可得到P点的坐标表达式。其中∠ABC和∠BAC的求法如下:
主要就是通过点积求得角度。
接下来就是通过代码来具体实现一下,看下我们推导是否正确:
using UnityEngine;
public class TriangleInsideCenter : MonoBehaviour
{
public Transform TA;
public Transform TB;
public Transform TC;
public Transform TP;
void Start()
{
float deg = 30f;
float sin = Mathf.Sin(deg * Mathf.Deg2Rad);
float cos = Mathf.Cos(deg * Mathf.Deg2Rad);
float arcsin = Mathf.Asin(sin) * Mathf.Rad2Deg;
float arccos = Mathf.Acos(cos) * Mathf.Rad2Deg;
}
void Update()
{
Vector3 p = CalculateInsideCenter(TA.position, TB.position, TC.position);
TP.position = p;
#if UNITY_EDITOR
Debug.DrawLine(TA.position, TB.position, Color.black);
Debug.DrawLine(TB.position, TC.position, Color.black);
Debug.DrawLine(TC.position, TA.position, Color.black);
Debug.DrawLine(TA.position, p, Color.white);
Debug.DrawLine(TB.position, p, Color.white);
Debug.DrawLine(TC.position, p, Color.white);
#endif
}
private Vector3 CalculateInsideCenter(Vector3 A, Vector3 B, Vector3 C)
{
Vector3 AB = B - A;
Vector3 AC = C - A;
Vector3 BA = A - B;
Vector3 BC = C - B;
Vector3 nBA = BA.normalized;
Vector3 nBC = BC.normalized;
float radBAC = Mathf.Acos(Vector3.Dot(AB, AC) / (AB.magnitude * AC.magnitude));
float radABC = Mathf.Acos(Vector3.Dot(BA, BC) / (BA.magnitude * BC.magnitude));
float halfRadBAC = radBAC / 2f;
float halfRadABC = radABC / 2f;
float r2 = AB.magnitude / (Mathf.Cos(halfRadBAC) * Mathf.Sin(halfRadABC) / Mathf.Sin(halfRadBAC) + Mathf.Cos(halfRadABC));
Vector3 P = ((nBA + nBC) / 2f).normalized * r2 + B;
return P;
}
}
效果如图:
估计这种看不出来结果是否正确,我们得将内心P到△ABC每条边的垂点和模长计算出来才行,如下:
可以根据向量表达式和点积以及一元二次方程求根得到垂点D的表达式,接下来通过代码实现如下:
using UnityEngine;
public class TriangleInsideCenter : MonoBehaviour
{
public Transform TA;
public Transform TB;
public Transform TC;
public Transform TP;
void Start()
{
float deg = 30f;
float sin = Mathf.Sin(deg * Mathf.Deg2Rad);
float cos = Mathf.Cos(deg * Mathf.Deg2Rad);
float arcsin = Mathf.Asin(sin) * Mathf.Rad2Deg;
float arccos = Mathf.Acos(cos) * Mathf.Rad2Deg;
}
void Update()
{
Vector3 A = TA.position;
Vector3 B = TB.position;
Vector3 C = TC.position;
Vector3 P = CalculateInsideCenter(TA.position, TB.position, TC.position);
TP.position = P;
#if UNITY_EDITOR
Debug.DrawLine(A, B, Color.black);
Debug.DrawLine(B, C, Color.black);
Debug.DrawLine(C, A, Color.black);
Vector3 D = CalculateVerticalVertex(A, B, P);
Vector3 E = CalculateVerticalVertex(B, C, P);
Vector3 F = CalculateVerticalVertex(C, A, P);
Debug.DrawLine(D, P, Color.white);
Debug.DrawLine(E, P, Color.white);
Debug.DrawLine(F, P, Color.white);
Debug.LogFormat("DP = {0} EP = {1} FP = {2}", Vector3.Distance(D, P), Vector3.Distance(E, P), Vector3.Distance(F, P));
#endif
}
private Vector3 CalculateInsideCenter(Vector3 A, Vector3 B, Vector3 C)
{
Vector3 AB = B - A;
Vector3 AC = C - A;
Vector3 BA = A - B;
Vector3 BC = C - B;
Vector3 nBA = BA.normalized;
Vector3 nBC = BC.normalized;
float radBAC = Mathf.Acos(Vector3.Dot(AB, AC) / (AB.magnitude * AC.magnitude));
float radABC = Mathf.Acos(Vector3.Dot(BA, BC) / (BA.magnitude * BC.magnitude));
float halfRadBAC = radBAC / 2f;
float halfRadABC = radABC / 2f;
float r2 = AB.magnitude / (Mathf.Cos(halfRadBAC) * Mathf.Sin(halfRadABC) / Mathf.Sin(halfRadBAC) + Mathf.Cos(halfRadABC));
Vector3 P = ((nBA + nBC) / 2f).normalized * r2 + B;
return P;
}
private Vector3 CalculateVerticalVertex(Vector3 A, Vector3 B, Vector3 P)
{
Vector3 AB = B - A;
Vector3 nAB = AB.normalized;
float Xn = nAB.x;
float Yn = nAB.y;
float Zn = nAB.z;
float Xa = A.x;
float Ya = A.y;
float Za = A.z;
float Xp = P.x;
float Yp = P.y;
float Zp = P.z;
float a = Xn * Xn + Yn * Yn + Zn * Zn;
float b = Xn * Xa - Xn * Xp + Yn * Ya - Yn * Yp + Zn * Za - Zn * Zp;
float c = 0;
float[] rs = CalculateQuadraticEquation(a, b, c);
Vector3 D = Vector3.zero;
//剔除模长r为0的情况
if (rs[0] != 0)
{
D = nAB * rs[0] + A;
}
else if (rs[1] != 0)
{
D = nAB * rs[1] + A;
}
return D;
}
private float[] CalculateQuadraticEquation(float a, float b, float c)
{
float x1 = (-b + Mathf.Sqrt(b * b - 4 * a * c)) / (2 * a);
float x2 = (-b - Mathf.Sqrt(b * b - 4 * a * c)) / (2 * a);
return new float[]
{
x1,
x2
};
}
}
最后效果如下:
可以通过图形和打印看得出来结果正确。