自然语言处理学习笔记-lecture07-句法分析01
句法分析(syntactic parsing)的任务就是识别句子的句法结构(syntactic structure)。包含短语结构分析 (Phrase parsing)和依存句法分析 (Dependency parsing)
短语结构分析
英语中的结构歧义随介词短语组合个数的增加而不断加深的,这个组合个数我们称之为开塔兰数(Catalan number,记作 C N C_N CN)。如果句子中存在这样 n n n ( n n n为自然数)个介词短语, C N C_N CN 可由下式获得:
C N = ( 2 n n ) 1 n + 1 = ( 2 n ) ! ( n ! ) 2 ( n + 1 ) C_N = \left(\begin{matrix}2n \\ n\end{matrix}\right)\frac{1}{n + 1} = \frac{(2n)!}{(n!)^2(n + 1)} CN=(2nn)n+11=(n!)2(n+1)(2n)!
基本方法和开源的句法分析器:
基于CFG规则的分析方法:
- 线图分析法 (chart parsing)
- CYK 算法
- Earley (厄尔利)算法
- LR算法/Tomita算法 …
Top-down: Depth-first/Breadth-first
Bottom-up
基于 PCFG 的分析方法
线性分析图
包括三种策略:自底向上、从上到下、从上到下和从下到上结合
自底向上的 Chart 分析算法
给定一组CFG规则: X P → α 1 ⋯ α n , n ≥ 1 XP\rightarrow \alpha_1\cdots \alpha_n,n \geq 1 XP→α1⋯αn,n≥1,句子的词性序列 S = W 1 W 2 ⋯ W n S = W_1W_2\cdots W_n S=W1W2⋯Wn,构造一个线图,一组节点和边的集合,之后建立一个二维表,记录每一条边的起始位置和终止位置,执行操作:查看任意相邻几条边上的词性串是否与某条重写规则的右部相同,如果相同,则增加一条新的边跨越原来相应的边,新增加边上的标记为这条重写规则的头(左部)。重复这个过程,直到没有新的边产生。
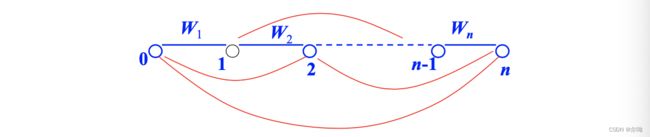
点规则:用于表示规则右部被归约(reduce)的程度。活性边(活动弧):规则右部未被完全匹配,非活性边(非活动弧, 或完成弧):规则右部已被完全匹配
例如给规则集:
![]()
对应的分析结果:再分析之前完成了形态分析和词性标注

将上面的图的边变为节点,将节点变为边,得到一棵树:

- 线图(Chart):保存分析过程中已经建立的成分(包括终结符和非终结符)、位置(包括起点和终点)。通常以 n × n n\times n n×n 的数组表示( n n n 为句子包含的词数)。
- 代理表(待处理表)(Agenda):记录刚刚得到的一些重写规则所代表的成分,这些重写规则的右端符号串与输入词性串(或短语标志串)中的一段完全匹配, 通常以栈或线性队列表示。
- 活动边集(ActiveArc):记录那些右端符号串与输入串的某一段相匹配,但还未完全匹配的重写规则,通常以数组或列表存储。
算法描述:从输入串的起始位置到最后位置,循环执行如下步骤:
- 如果待处理表(Agenda)为空,则找到下一个位置上的词,将该词对应的(所有)词类 X X X 附以 ( i , j ) (i, j) (i,j) 作为元素放到待处理表中,即 X ( i , j ) X (i, j) X(i,j)。其中, i , j i, j i,j 分别是该词的起始位置和终止位置, j > i , j − i j > i,j - i j>i,j−i 为该词的长度。最多执行的次数为: C C C
- 从 Agenda 中取出一个元素 X ( i , j ) X(i, j) X(i,j),最多执行的次数为: 1 1 1
- 对于每条规则 A → X γ A \rightarrow X\gamma A→Xγ,将 A → X ∘ γ ( i , j ) A \rightarrow X \circ \gamma(i,j) A→X∘γ(i,j)加入活动边集ActiveArc 中,然后调用扩展弧子程序,最多执行的次数为: S n 2 Sn^2 Sn2
扩展弧子程序:
- 将 X X X 插入图表(Chart)的 ( i , j ) (i, j) (i,j) 位置中,最多执行的次数为: 1 1 1
- 对于活动边集(ActiveArc)中每个位置为 ( k , i ) ( 1 ≤ k < i ) (k, i) (1≤k(k,i)(1≤k<i) 的点规则,如果该规则具有如下形式: A → α ∘ X A \rightarrow\alpha\circ X A→α∘X , 如果 A = S A=S A=S, 则把 S ( 1 , n + 1 ) S(1, n+1) S(1,n+1) 加入到 Chart 中,并给出一个完整的分析结果;否则,则将 A ( k , j ) A(k, j) A(k,j) 加入到Agenda表中。最多执行的次数为: S n 2 Sn^2 Sn2
- 对于每个位置为 ( k , i ) (k, i) (k,i)的点规则: A → α ∘ X β A\rightarrow\alpha\circ X\beta A→α∘Xβ,则将 A → α X ∘ β ( k , j ) A\rightarrow\alpha X\circ\beta(k,j) A→αX∘β(k,j)加入到活动边集中,最多执行的次数为: S n 2 Sn^2 Sn2
算法的时间复杂度分析
设 n n n为输入句子的长度, C C C 为上下文无关文法中的非终结符的数目, S S S 为点规则的状态数目(大于 C F G CFG CFG 规则的数目),显然 S > C S > C S>C。因为 Agenda 表中的元素形式为 X ( i , j ) X(i, j) X(i,j),因此, Agenda 表中最大的元素个数为: C n 2 Cn^2 Cn2。由于ActiveArc 中的元素形式为: A → α ∘ X ( i , j ) A\rightarrow\alpha\circ X(i,j) A→α∘X(i,j),所以ActiveArc 表中最大的元素数目为: S n 2 Sn^2 Sn2,Chart 表中的边的形式为: A ( i , j ) A(i, j) A(i,j),因此,Chart 表中最大的元素数目为: C n 2 Cn^2 Cn2。由于算法对于长度为 n 的输入句子要执行 n 次循环,因此,Chart 算法最大执行的操作次数为: O ( K n 3 ) O(Kn^3) O(Kn3)
优点:算法简单
弱点:算法效率低,需要高质量的规则,分析结果与规则质量密切相关;难以区分歧义结构。
CYK分析算法
Coke-Younger-Kasami (CYK) 算法
- 对Chomsky 文法进行范式化:
- 自下而上的分析方法
- 构造 ( n + 1 ) × ( n + 1 ) (n+1)\times(n+1) (n+1)×(n+1)的识别矩阵, n n n为输入句子长度,假设输入句子 x = w 1 w 2 ⋯ w n , w i x = w_1w_2\cdots w_n,w_i x=w1w2⋯wn,wi为构成句子的单词 n = ∣ x ∣ n = |x| n=∣x∣
其中识别矩阵构成:方阵对角线以下全部为0,主对角线以上的元素由文法G的非终结符构成,主对角线上的元素由输入句子的终结符号(单词)构成,构造步骤如下:
- 首先构造主对角线,令 t 0 , 0 = 0 t_{0,0}=0 t0,0=0,然后,从 t 1 , 1 t_{1,1} t1,1 到 t n , n t_{n,n} tn,n,在主对角线的位置上依次放入输入句子 x x x 的单词 w i w_i wi。
- 构造主对角线以上紧靠主对角线的元素 t i , i + 1 t_{i,i+1} ti,i+1,其中 i = 0 , 1 , 2 , ⋯ , n − 1 i = 0,1,2,\cdots,n - 1 i=0,1,2,⋯,n−1,对于输入句子 x = w 1 w 2 ⋯ w n x = w_1w_2\cdots w_n x=w1w2⋯wn,从 w 1 w_1 w1开始分析
假设在文法G 的产生式集中有一条规则: A → w 1 A\rightarrow w_1 A→w1则 t 0 , 1 = A t_{0,1} = A t0,1=A,以此类推,如果有 A → w i + 1 A\rightarrow w_{i + 1} A→wi+1则 t i , i + 1 = A t_{i,i+1} = A ti,i+1=A - 按平行于主对角线的方向,一层一层的向上填写矩阵的各个元素 t i , j t_{i,j} ti,j,其中 i = 0 , 1 , ⋯ , n − d , j = d + i , d = 2 , 3 , ⋯ , n i = 0, 1,\cdots,n-d,j = d+i,d = 2,3,\cdots,n i=0,1,⋯,n−d,j=d+i,d=2,3,⋯,n,如果存在一个正整数 k , i + 1 ≤ k ≤ j − 1 k,i+1\leq k\leq j-1 k,i+1≤k≤j−1,在文法 G G G的规则集中有产生式 A → B C A\rightarrow BC A→BC,并且 B ∈ t i , k , C ∈ t k , j B\in t_{i,k},C\in t_{k,j} B∈ti,k,C∈tk,j那么将 A A A写到矩阵 t i j t_{ij} tij位置上,判断句子 x x x由文法 G G G所产生的充要条件是 t 0 , n = S t_{0,n} = S t0,n=S
以“他/P 喜欢/V 读/V 书/N”为例:
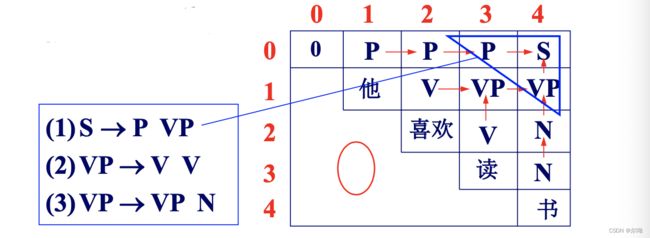
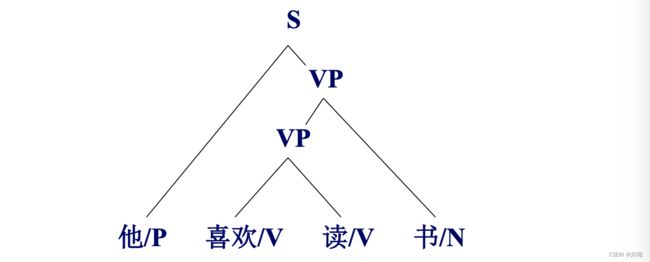
优点:简单易行
弱点:必须对文法进行范式化处理,无法区分歧义
概率上下文无关文法
形式: A → α , p A\rightarrow \alpha,p A→α,p
约束: ∑ α p ( A → α ) = 1 \sum_\alpha p(A\rightarrow\alpha) = 1 ∑αp(A→α)=1
计算分析树概率的基本假设
- 位置不变性:子树的概率与其管辖的词在整个句子中所处的位置无关,即对于任意的 k , p ( A k ( k + C ) → w ) k,p(A_{k(k + C)}\rightarrow w) k,p(Ak(k+C)→w)一样
- 上下文无关性:子树的概率与子树管辖范围以外的词无关,即 p ( A k l → w ∣ 任何超出 k ∼ l 范围的上下文 ) = p ( A k l → w ) p(A_{kl}\rightarrow w|任何超出k\sim l范围的上下文) = p(A_{kl}\rightarrow w) p(Akl→w∣任何超出k∼l范围的上下文)=p(Akl→w)
- 祖先无关性:子树的概率与推导出该子树的祖先结点无关,即 p ( A k l → w ∣ 任何除 A 以外的祖先结点 ) = p ( A k l → w ) p(A_{kl}\rightarrow w|任何除 A 以外的祖先结点) = p(A_{kl}\rightarrow w) p(Akl→w∣任何除A以外的祖先结点)=p(Akl→w)
句法分析树的概率计算方法示例:
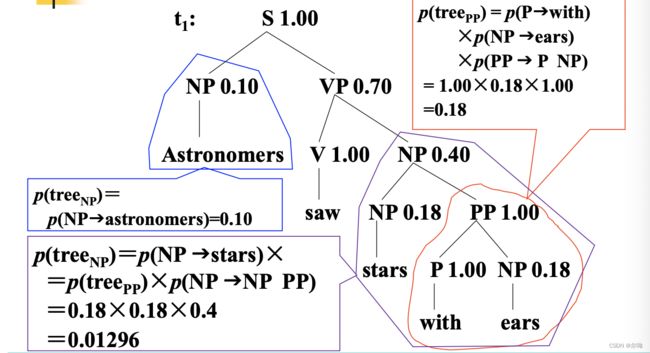
对于给定的句子 S S S ,两棵句法分析树的概率不等, P ( t 1 ) > P ( t 2 ) P(t_1) > P(t_2) P(t1)>P(t2),因此,可以得出结论:分析结果 t 1 t_1 t1正确的可能性大于 t 2 t_2 t2。
PCFG的三个问题
- 给定句子 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn和PCFG G G G,如何快速的计算 p ( W ∣ G ) p(W|G) p(W∣G)
- 给定句子 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn和PCFG G G G,如何快速地选择最佳句法结构树?
- 给定句子 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn和PCFG G G G,如何调节 G G G的参数,使得 p ( W ∣ G ) p(W|G) p(W∣G)最大
假设文法 G ( S ) G(S) G(S)的规则只有两种形式:
A → w , w ∈ V T A → B C , B , C ∈ V N A\rightarrow w,w\in V_T \\ A\rightarrow BC,B,C\in V_N A→w,w∈VTA→BC,B,C∈VN
可以通过范式化处理,使CFG 规则满足上述形式。这种假设的文法形式称为乔姆斯基范式(Chomsky normal form, CNF)。
内向算法或外向算法
解决第一个问题-快速地计算句子的句法树概率
内向算法
基本思想:利用动态规划算法计算由非终结符 A 推导出的某个字串片段 w i w i + 1 ⋯ w j w_iw_{i + 1}\cdots w_j wiwi+1⋯wj的概率 α i j ( A ) \alpha_{ij}(A) αij(A),语句 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn的概率即为文法 G ( S ) G(S) G(S)中 S S S推导出的字串的概率 α 1 n ( S ) \alpha_{1n}(S) α1n(S)
α i j ( A ) = p ( A ⇒ w i w i + 1 ⋯ w j ) \alpha_{ij}(A) = p(A\Rightarrow w_iw_{i + 1}\cdots w_j) αij(A)=p(A⇒wiwi+1⋯wj)
计算 α i j ( A ) \alpha_{ij}(A) αij(A)的递推公式:
α i i ( A ) = p ( A → w i ) α i j ( A ) = ∑ B , C ∈ V N ∑ i ≤ k ≤ j p ( A → B C ) α i k ( B ) α ( k + 1 ) j ( C ) \alpha_{ii}(A) = p(A\rightarrow w_i) \\ \alpha_{ij}(A) = \sum_{B,C\in V_N}\sum_{i\leq k\leq j}p(A\rightarrow BC)\alpha_{ik}(B)\alpha_{(k + 1)j}(C) αii(A)=p(A→wi)αij(A)=B,C∈VN∑i≤k≤j∑p(A→BC)αik(B)α(k+1)j(C)
内向算法描述:
输入:文法 G ( S ) G(S) G(S),语句 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn
输出: p ( S ⇒ w 1 w 2 ⋯ w n ) p(S\Rightarrow w_1w_2\cdots w_n) p(S⇒w1w2⋯wn)
- 初始化: α i i ( A ) = p ( A → w i ) , A ∈ V N , 1 ≤ i ≤ j ≤ n \alpha_{ii}(A) = p(A\rightarrow w_i),A\in V_N,1\leq i\leq j\leq n αii(A)=p(A→wi),A∈VN,1≤i≤j≤n
- 归纳计算: j = 1 , ⋯ , n , i = 1 , ⋯ , n − j , j = 1,\cdots,n,i = 1,\cdots,n - j, j=1,⋯,n,i=1,⋯,n−j,重复下列计算:外层循环为 j j j
α i ( i + j ) ( A ) = ∑ B , C ∈ V N ∑ i ≤ k ≤ i + j p ( A → B C ) α i k ( B ) α ( k + 1 ) ( i + j ) ( C ) \alpha_{i(i+j)}(A) = \sum_{B,C\in V_N}\sum_{i\leq k\leq i + j}p(A\rightarrow BC)\alpha_{ik}(B)\alpha_{(k + 1)(i + j)}(C) αi(i+j)(A)=B,C∈VN∑i≤k≤i+j∑p(A→BC)αik(B)α(k+1)(i+j)(C) - 终结: p ( S ⇒ w 1 w 2 ⋯ w n ) = α 1 n ( S ) p(S\Rightarrow w_1w_2\cdots w_n) = \alpha_{1n}(S) p(S⇒w1w2⋯wn)=α1n(S)
外向算法
定义:外向变量 β i j ( A ) \beta_{ij}(A) βij(A)是文法初始符号 S S S推导出语句 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn的过程中,到达扩展符号串 w 1 ⋯ w i − 1 A w j + 1 ⋯ w n w_1\cdots w_{i - 1}Aw_{j + 1}\cdots w_n w1⋯wi−1Awj+1⋯wn的概率 ( A = w i ⋯ w j ) (A = w_i\cdots w_j) (A=wi⋯wj)
β i j ( A ) = p ( S ⇒ w 1 ⋯ w i − 1 A w j + 1 ⋯ w n ) \beta_{ij}(A) = p(S\Rightarrow w_1\cdots w_{i - 1}Aw_{j + 1}\cdots w_n) βij(A)=p(S⇒w1⋯wi−1Awj+1⋯wn)
β i j ( A ) \beta_{ij}(A) βij(A)表示除了以 A A A为根节点的子树以外的概率,其递推公式:
β 1 n ( A ) = δ ( A , S ) β i j ( A ) = ∑ B , C ∑ k > j β i k ( B ) p ( B → A C ) α ( j + 1 ) k ( C ) + ∑ B , C ∑ k < i β k j ( B ) p ( B → C A ) α k ( i − 1 ( C ) \beta_{1n}(A) = \delta(A,S) \\ \beta_{ij}(A) = \sum_{B,C}\sum_{k \gt j}\beta_{ik}(B)p(B\rightarrow AC)\alpha_{(j + 1)k}(C) + \sum_{B,C}\sum_{k \lt i}\beta_{kj}(B)p(B\rightarrow CA)\alpha_{k(i - 1}(C) β1n(A)=δ(A,S)βij(A)=B,C∑k>j∑βik(B)p(B→AC)α(j+1)k(C)+B,C∑k<i∑βkj(B)p(B→CA)αk(i−1(C)
相应的示意图:
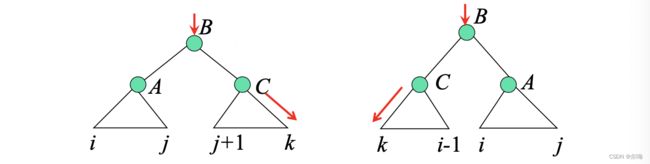
外向算法描述:
输入:PCFG G = ( S , N , T , P ) G = (S,N,T,P) G=(S,N,T,P),语句 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn
输出: β i j ( A ) , A ∈ N , 1 ≤ i ≤ j ≤ n \beta_{ij}(A),A\in N,1\leq i\leq j\leq n βij(A),A∈N,1≤i≤j≤n
- 初始化: β 1 n ( A ) = δ ( A , S ) , A ∈ N \beta_{1n}(A) = \delta(A,S),A\in N β1n(A)=δ(A,S),A∈N
- 归纳: j j j从 n − 1 n - 1 n−1到 0 0 0, i i i从 1 1 1到 n − j n - j n−j,重复计算:
β i ( i + j ) ( A ) = ∑ B , C ∑ i + j < k ≤ n p ( B → A C ) α ( i + j + 1 ) k ( C ) β i k ( B ) + ∑ B , C ∑ 1 ≤ k < i p ( B → C A ) α k ( i − 1 ( C ) β k ( i + j ) ( B ) \beta_{i(i + j)}(A) = \sum_{B,C}\sum_{i + j \lt k \leq n}p(B\rightarrow AC)\alpha_{(i + j + 1)k}(C)\beta_{ik}(B) + \sum_{B,C}\sum_{1 \leq k \lt i}p(B\rightarrow CA)\alpha_{k(i - 1}(C)\beta_{k(i + j)}(B) βi(i+j)(A)=B,C∑i+j<k≤n∑p(B→AC)α(i+j+1)k(C)βik(B)+B,C∑1≤k<i∑p(B→CA)αk(i−1(C)βk(i+j)(B) - 终结: p ( S ⇒ w 1 w 2 ⋯ w n ) = β 1 n ( S ) p(S\Rightarrow w_1w_2\cdots w_n) = \beta_{1n}(S) p(S⇒w1w2⋯wn)=β1n(S)
Viterbi 算法
解决第二个问题-最佳分析结果搜索
Viterbi 变量 γ i j ( A ) \gamma_{ij}(A) γij(A)是由非终结符 A A A 推导出语句 W W W中子字串 w i w i + 1 ⋯ w j w_{i}w_{i + 1}\cdots w_j wiwi+1⋯wj的最大概率。变量 ψ i , j \psi_{i,j} ψi,j用于记忆字串 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn的Viterbi 语法分析结果。
Viterbi 算法描述:
输入:文法 G ( S ) G(S) G(S),语句 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn
输出: γ 1 n ( S ) \gamma_{1n}(S) γ1n(S)
- 初始化: γ i i ( A ) = p ( A → w i ) , A ∈ V N , 1 ≤ i ≤ j ≤ n \gamma_{ii}(A) = p(A\rightarrow w_i),A \in V_N,1\leq i\leq j \leq n γii(A)=p(A→wi),A∈VN,1≤i≤j≤n
- 归纳计算: j = 1 ⋯ n , i = 1 ⋯ n − j j = 1\cdots n,i = 1\cdots n-j j=1⋯n,i=1⋯n−j重复下列计算:
γ i ( i + j ) ( A ) = m a x B , C ∈ V N ; i ≤ k ≤ i + j p ( a → B C ) γ i k ( B ) γ ( k + 1 ) ( i + j ) ( C ) ψ i ( i + j ) ( A ) = a r g m a x B , C ∈ V N ; i ≤ k ≤ i + j p ( a → B C ) γ i k ( B ) γ ( k + 1 ) ( i + j ) ( C ) \gamma_{i(i+j)}(A) = \mathop{max}\limits_{B,C\in V_N;i\leq k\leq i + j}p(a\rightarrow BC)\gamma_{ik}(B)\gamma_{(k + 1)(i + j)}(C) \\ \psi_{i(i+j)}(A) = \mathop{arg\ max}\limits_{B,C\in V_N;i\leq k\leq i + j}p(a\rightarrow BC)\gamma_{ik}(B)\gamma_{(k + 1)(i + j)}(C) γi(i+j)(A)=B,C∈VN;i≤k≤i+jmaxp(a→BC)γik(B)γ(k+1)(i+j)(C)ψi(i+j)(A)=B,C∈VN;i≤k≤i+jarg maxp(a→BC)γik(B)γ(k+1)(i+j)(C) - 终结: p ( S ⇒ w 1 w 2 ⋯ w n ) = γ 1 n ( S ) p(S\Rightarrow w_1w_2\cdots w_n) = \gamma_{1n}(S) p(S⇒w1w2⋯wn)=γ1n(S)
内外向算法
解决第三个问题-参数估计
基本思路:如果有大量已标注语法结构的训练语料,则可直接通过计算每个语法规则的使用次数,用最大似然估计方法计算 PCFG 规则的概率参数,即:
p ^ ( N j → ζ ) = C ( N j → ζ ) ∑ γ C ( N j → γ ) \hat p(N^j\rightarrow \zeta) = \frac{C(N^j\rightarrow \zeta)}{\sum_\gamma C(N^j\rightarrow \gamma)} p^(Nj→ζ)=∑γC(Nj→γ)C(Nj→ζ)
多数情况下,没有可利用的标注语料,只好借助 EM (Expectation Maximization) 迭代算法估计PCFG的 概率参数。
初始时随机地给参数赋值,得到语法G0,依据 G0 和训练语料,得到语法规则使用次数的期望值,以期望次数运用于最大似然估计,得到语法参数新的估计值,由此得到新的语法 G1,由 G1 再次得到语法规则的使用次数的期望值,然后又可以重新估计语法参数。循环这个过程,语法参数将收敛于最大似然估计值。
例如给定CFG G G G和训练数据 W = w 1 w 2 ⋯ w n W = w_1w_2\cdots w_n W=w1w2⋯wn,语法规则 A → B C A\rightarrow BC A→BC使用次数的期望值为:
C o u n t ( A → B C ) = ∑ 1 ≤ i ≤ k ≤ j ≤ n p ( A i j , B i k , C ( k + 1 ) j ∣ w 1 ⋯ w n , G ) = 1 p ( w 1 ⋯ w n ∣ G ) ∑ 1 ≤ i ≤ k ≤ j ≤ n p ( A i j , B i k , C ( k + 1 ) j , w 1 ⋯ w n ∣ G ) = 1 p ( w 1 ⋯ w n ∣ G ) ∑ 1 ≤ i ≤ k ≤ j ≤ n β i j ( A ) p ( A → B C ) α i k ( B ) α ( k + 1 ) j ( C ) \begin{aligned} Count(A\rightarrow BC) &= \sum_{1\leq i\leq k\leq j\leq n}p(A_{ij},B_{ik},C_{(k + 1)j}|w_1\cdots w_n,G) \\ &= \frac{1}{p(w_1\cdots w_n|G)} \sum_{1\leq i\leq k\leq j\leq n}p(A_{ij},B_{ik},C_{(k + 1)j},w_1\cdots w_n|G) \\ &= \frac{1}{p(w_1\cdots w_n|G)} \sum_{1\leq i\leq k\leq j\leq n}\beta_{ij}(A)p(A\rightarrow BC)\alpha_{ik}(B)\alpha_{(k + 1)j}(C) \end{aligned} Count(A→BC)=1≤i≤k≤j≤n∑p(Aij,Bik,C(k+1)j∣w1⋯wn,G)=p(w1⋯wn∣G)11≤i≤k≤j≤n∑p(Aij,Bik,C(k+1)j,w1⋯wn∣G)=p(w1⋯wn∣G)11≤i≤k≤j≤n∑βij(A)p(A→BC)αik(B)α(k+1)j(C)
类似地,语法规则 A → a A\rightarrow a A→a 的使用次数的期望值为:
C o u n t ( A → a ) = ∑ 1 ≤ i ≤ n p ( A i i ∣ w 1 ⋯ w n , G ) = 1 p ( w 1 ⋯ w n ∣ G ) ∑ 1 ≤ i ≤ n p ( A i i , w 1 ⋯ w n ∣ G ) = 1 p ( w 1 ⋯ w n ∣ G ) ∑ 1 ≤ i ≤ n β i i ( A ) p ( A → a ) δ ( a , w i ) \begin{aligned} Count(A\rightarrow a) &= \sum_{1\leq i\leq n}p(A_{ii}|w_1\cdots w_n,G) \\ &= \frac{1}{p(w_1\cdots w_n|G)}\sum_{1\leq i\leq n}p(A_{ii},w_1\cdots w_n|G) \\ &= \frac{1}{p(w_1\cdots w_n|G)}\sum_{1\leq i\leq n}\beta{ii}(A)p(A\rightarrow a)\delta(a,w_i) \end{aligned} Count(A→a)=1≤i≤n∑p(Aii∣w1⋯wn,G)=p(w1⋯wn∣G)11≤i≤n∑p(Aii,w1⋯wn∣G)=p(w1⋯wn∣G)11≤i≤n∑βii(A)p(A→a)δ(a,wi)
G 的参数可由下面的公式重新估计:
p ^ ( A → μ ) = C o u n t ( A → μ ) ∑ μ C o u n t ( A → μ ) \hat p(A\rightarrow \mu) = \frac{Count(A\rightarrow \mu)}{\sum_{\mu}Count(A\rightarrow \mu)} p^(A→μ)=∑μCount(A→μ)Count(A→μ)
其中 μ \mu μ要么是终结符号,要么是两个非终结符号串,即 A → μ A\rightarrow \mu A→μ为乔姆斯基语法范式要求的两种形式。
内外向算法:
- 初始化:随机给 p ( A → μ ) p(A\rightarrow \mu) p(A→μ),使加和为1,由此得到语法 G 0 G_0 G0,令 i = 0 i = 0 i=0
- EM迭代:
E步:由 G i G_i Gi根据上面的求期望值公式得到两个期望值
M步:由M步得到的期望值,重新估计 p ( A → μ ) p(A\rightarrow \mu) p(A→μ),得到 G i + 1 G_{i + 1} Gi+1 - 循环:重复EM步骤,直到 p ( A → μ ) p(A\rightarrow \mu) p(A→μ)收敛。
PCFG的优点:可利用概率减少分析过程的搜索空间;可利用概率对概率较小的子树剪枝,加快分析效率;可以定量地比较两个语法的性能。
弱点:分析树的概率计算条件非常苛刻,甚至不够合理。
短语结构分析方法评估
内部评测 (intrinsic evaluation)-对评测方法本身的评测,用于指导句法分析系统及其语法的开发过程。主要指标有:
- 语法的覆盖性 (grammatical coverage)
- 平均分析基数 (average parse base)
- 结构一致性 (structural consistency)
- 排序的一致性 (best-first/ranked consistency)等
对比评测 (comparative evaluation ):用于对比不同系统之间的性能差别,主要评测指标和方法包括:
- 树相似性 (tree similarity)
- 模型的熵 (或困惑度) (entropy/perplexity)
- 语法评估兴趣小组 (grammar evaluation interest group, GIEG)的评测方案等
句法分析器性能评测:目前使用比较广泛的句法分析器评价指标是PARSEVAL测度,三个基本的评测指标:
- 精度(precision):句法分析结果中正确的短语个数所占的比例,即分析结果中与标准分析树(答案)中的短语相匹配的个数占分析结果中所有短语个数的比例
- 召回率(recall):句法分析结果中正确的短语个数占标准分析树中全部短语个数的比例
- F-measure
- 交叉括号数 (crossing brackets):一棵分析树中与其他分析树中边界相交叉的成分个数的平均值。
分析树中除了词性标注符号以外的其他非终结符节点通常采用如下标记格式:XP-(起始位置:终止位置)。其中,XP为短语名称;(起始位置:终止位置)为该节点的跨越范围,起始位置指该节点所包含的子节点的起始位置,终止位置为该节点所包含的子节点的终止位置。在计算PARSEVAL指标时,通常需要计算分析结果与标准分析树之间括号匹配的数目或括号交叉的数目。
例如标准答案:S-(0:11), NP-(0:2), VP-(2:9), VP-(3:9), NP- (4:6), PP-(6:9), NP-(7:9), *NP-(9:10)
系统结果:S-(0:11), NP-(0:2), VP-(2:10), VP-(3:10), NP- (4:10), NP-(4:6), PP-(6:10), NP-(7:10)
只有加粗的短语和标准一样,所以:
P = 3 8 × 100 % = 37.5 % R = 3 8 × 100 % = 37.5 % P = \frac38\times 100\% = 37.5\% \\ R = \frac38\times 100\% = 37.5\% P=83×100%=37.5%R=83×100%=37.5%