统计学习方法01——概论

原文代码作者：https://github.com/wzyonggege/statistical-learning-method

目录

1.使用最小二乘法拟和曲线

1.1 最小二乘拟合（scipy.optimize.leastsq）

 1.1.1 画图显示中文标签和正负号

1.1.2 正态分布（np.random.randn） 

 1.1.3 scipy.linalg (线性代数)

 2. 多项式拟合目标函数

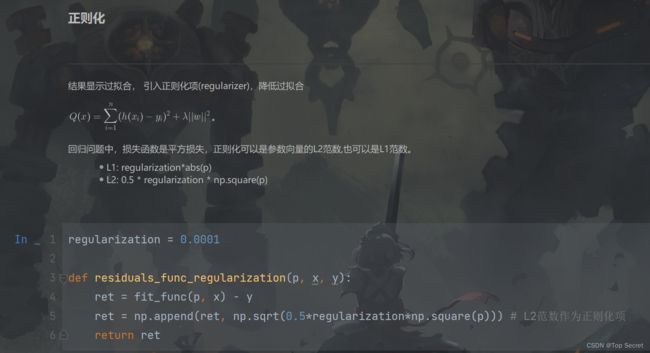
2.1 利用正则化降低过拟合的问题 

---

 

1.使用最小二乘法拟和曲线

 导包：

import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

1.1 最小二乘拟合（scipy.optimize.leastsq）

学习地址

from scipy.optimize import leastsq

参考代码：

import numpy as np
from scipy import linalg #线性代数计算
from scipy.optimize import leastsq #用于最小二乘拟合的库

#通过多项式拟合目标函数

# 被拟合的目标函数
def func(x,p):
    A,k,theta = p  # p的数据类型
    return A * np.sin(2 * np.pi * k * x + theta)

#下面代码是定义计算误差函数，计算实验数据想x、y和拟合函数之间的差，参数p为拟合需要找到的系数，同时添加噪声数据。

#计算误差函数
def residuals(p,y,x):
    return (y-func(x,p))

x = np.linspace(0,-2*np.pi,100)
A,k,theta = 10,0.34,np.pi/6  #真实数据的参数
y0 = func(x,[A,k,theta])  #真实数据
y1 = y0 + 2 * np.random.randn(len(x)) #加入噪声之后的实验数据
p0 = [7,0.2,0] #第一次猜测的函数拟合参数

# 调用leastsq拟合，residuals为计算误差函数，p0为拟合参数初始值，args为需要拟合的实验数据。
plsq = leastsq(residuals, p0, args=(y1, x))
print("真实参数:", [A, k, theta])
print("拟合参数:", plsq[0])
"""
真实参数: [10, 0.34, 0.5235987755982988]
拟合参数: [10.35804845  0.33960502  0.49450276]
"""
#通过绘制图像来观察数据拟合效果
import matplotlib.pyplot as plt
import pylab as pl

plt.rcParams['font.sans-serif'] = ['SimHei']          # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False            # 用来正常显示负号
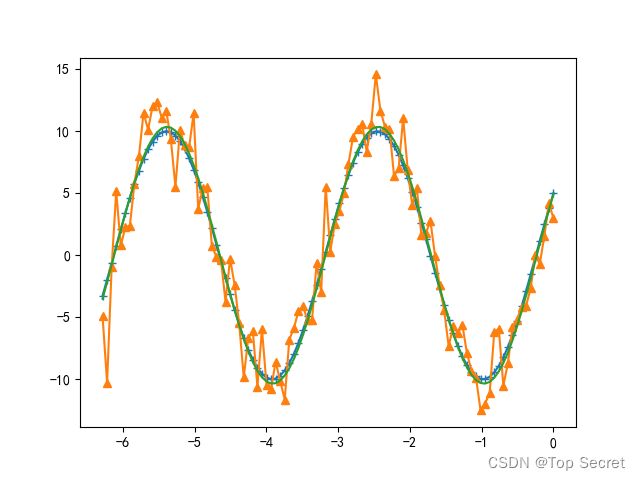
pl.plot(x, y0, marker='+', label=u"真实数据")
pl.plot(x, y1, marker='^', label=u"带噪声的实验数据")
pl.plot(x, func(x, plsq[0]), label=u"拟合数据")
pl.legend() #显示图例
pl.show()

 1.1.1 画图显示中文标签和正负号

plt.rcParams['font.sans-serif'] = ['SimHei']          # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False            # 用来正常显示负号 

1.1.2 正态分布（np.random.randn） 

 numpy.random.randn()用法_独正己身的博客-CSDN博客_random.randn

 1.1.3 scipy.linalg (线性代数)

python库01—scipy.linalg(线性代数)_Top Secret的博客-CSDN博客

 2. 多项式拟合目标函数

偷个懒：

# 第1章 统计学习方法概论
import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt

# 目标函数
def real_func(x):
    return np.sin(2*np.pi*x)

# 多项式
def fit_func(p, x):
    f = np.poly1d(p)
    return f(x)

# 残差
def residuals_func(p, x, y):
    ret = fit_func(p, x) - y
    return ret

# 十个点
x = np.linspace(0, 1, 10)
x_points = np.linspace(0, 1, 1000)
# 加上正态分布噪音的目标函数的值
y_ = real_func(x)
y = [np.random.normal(0, 0.1) + y1 for y1 in y_]

def fitting(M=0):
    """
    M    为 多项式的次数
    """
    # 随机初始化多项式参数
    p_init = np.random.rand(M + 1)
    # 最小二乘法
    p_lsq = leastsq(residuals_func, p_init, args=(x, y))
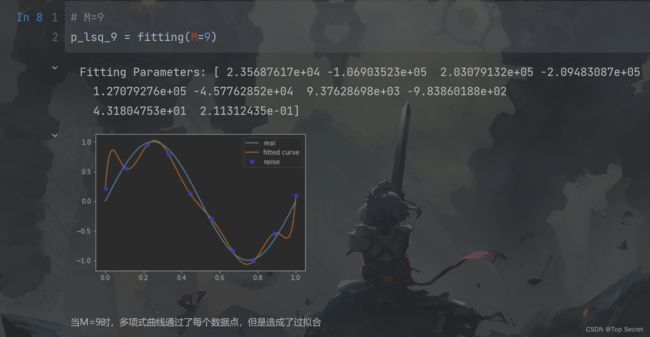
    print('Fitting Parameters:', p_lsq[0])

    # 可视化
    plt.plot(x_points, real_func(x_points), label='real')
    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
    plt.plot(x, y, 'bo', label='noise')
    plt.legend()
    return p_lsq

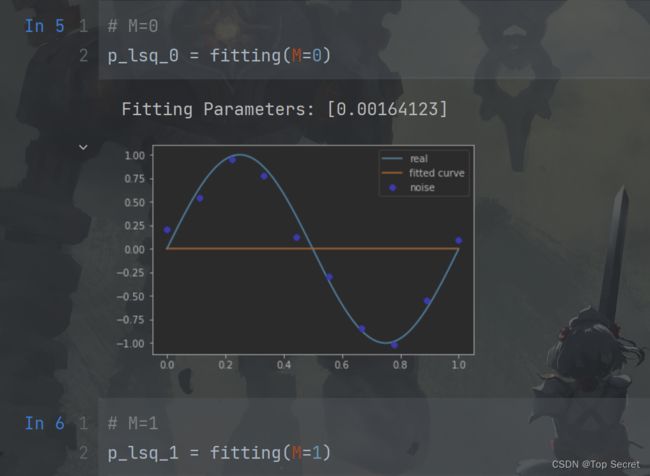
# M=0
p_lsq_0 = fitting(M=0)

2.1 利用正则化降低过拟合的问题