跟李沐学AI-动手学深度学习-现代卷积神经网络

深度卷积神经网络(AlexNet)

深度学习之前最火的是机器学习：

• 特征提取。
• 选择核函数来计算相关性。
• 凸优化问题。
• 漂亮的定理。

计算机视觉方面之前关注的不是机器学习而是几何学：

• 抽取特征。
• 描述几何（例如多相机），
• （非）凸优化。
• 漂亮定理。
• 假设满足了，效果很好。

在十几年前，计算机视觉中最重要的是特征工程：

• 特征工程是关键。
• 特征描述子：SIFT，SURF。
• 视觉词袋（聚类）。
• 最后用 SVM。

数据集ImageNet(2010)：自然物体的彩色图片。

AlexNet
赢得了2012年ImageNet竞赛。
是一个更大更深的LeNet。
主要改进点：丢弃法，ReLU，MaxPooling。
计算机视觉方法论的改变。

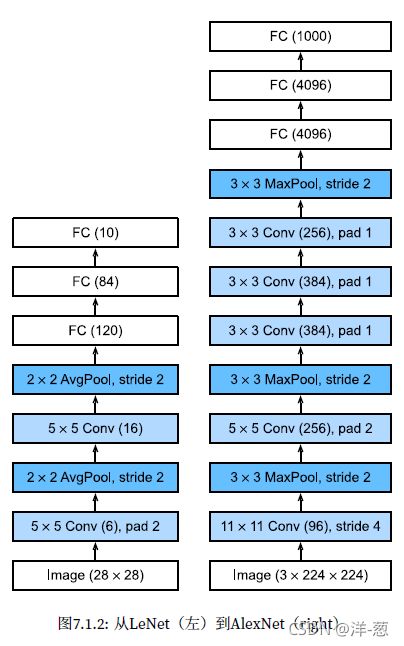
AlexNet架构

更大的池化层，使用了最大池化层。
更大的核窗口和步长，因为图片更大了。
新加了3层卷积层。
更多的输出通道。

更多细节

• 激活函数从sigmoid变成了ReLU（缓解梯度消失）。
• 隐藏全连接层后加入了丢弃层。
• 数据增强。

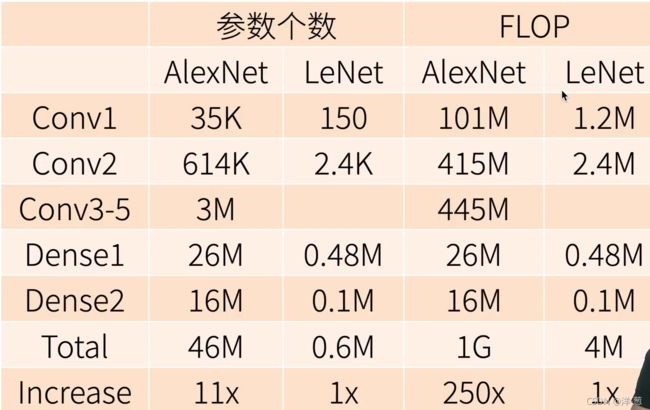
复杂度

总结

• AlexNet是更大更深的LeNet，10X参数个数，260X计算复杂度。
• 新进入了丢弃法，ReLU，最大池化层，和数据增强。
• AlexNet赢下了2012ImageNet竞赛后，标志着新的一轮神经网络热潮的开始。

深度卷积神经网络(AlexNet)代码实现

import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
	# 这⾥，我们使⽤⼀个11*11的更⼤窗⼝来捕捉对象。
	# 同时，步幅为4，以减少输出的⾼度和宽度。
	# 另外，输出通道的数⽬远⼤于LeNet
	nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), 					  nn.ReLU(),
	nn.MaxPool2d(kernel_size=3, stride=2),
	# 减⼩卷积窗⼝，使⽤填充为2来使得输⼊与输出的⾼和宽⼀致，且	增⼤输出通道数
	nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
	nn.MaxPool2d(kernel_size=3, stride=2),
	# 使⽤三个连续的卷积层和较⼩的卷积窗⼝。
	# 除了最后的卷积层，输出通道的数量进⼀步增加。
	# 在前两个卷积层之后，汇聚层不⽤于减少输⼊的⾼度和宽度
	nn.Conv2d(256, 384, kernel_size=3, padding=1), 	nn.ReLU(),
	nn.Conv2d(384, 384, kernel_size=3, padding=1), 	nn.ReLU(),
	nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
	nn.MaxPool2d(kernel_size=3, stride=2),
	nn.Flatten(),
	# 这⾥，全连接层的输出数量是LeNet中的好⼏倍。使⽤dropout层来减轻过度拟合
	nn.Linear(6400, 4096), nn.ReLU(),
	nn.Dropout(p=0.5),
	nn.Linear(4096, 4096), nn.ReLU(),
	nn.Dropout(p=0.5),
	# 最后是输出层。由于这⾥使⽤Fashion-MNIST，所以⽤类别数为10，⽽⾮论⽂中的1000
	nn.Linear(4096, 10))

我们构造一个 单通道数据，来观测每一层输出的形状。

X = torch.randn(1, 1, 224, 224)
for layer in net:
	X=layer(X)
	print(layer.__class__.__name__,'Output shape:\t',X.shape)

Fashion-MNIST图像的分辨率低于ImageNet图像。我们将他们增加到224*224。

batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

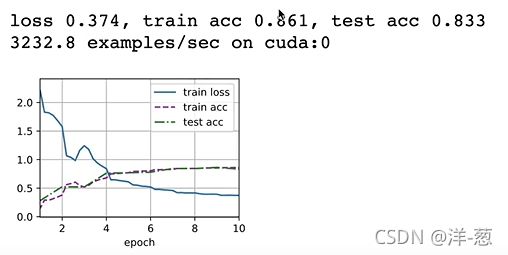
训练AlexNet

lr, num_epochs = 0.01, 10
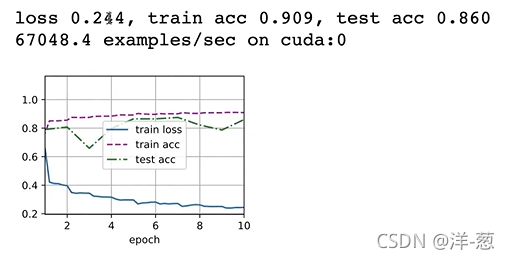
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

使用块的网络(VGG)

像上边的AlexNet长得不规则，比较随意，结构不那么清晰。
对于某一步的具体意义可能不会那么清晰。能否更大更深？
所以后来者也从以下方面思考了模型改进：

• 更多的全连接层（太贵）
• 更多的卷积层
• 将卷积层组合成块

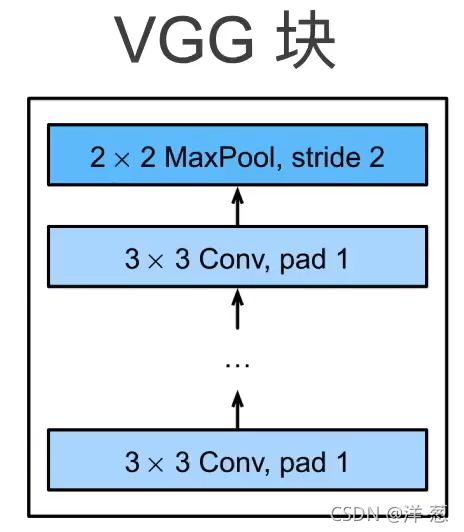
VGG块

深和宽的思考？
是使用55的卷积还是33的卷积？最后经过实验发现，深但窄的网络的效果更好。
VGG块：33卷积(填充1)(n层，m通道)，22最大池化层(步长2)。

VGG架构

多个VGG块后连全连接层。
不同次数的重复块得到不同的架构VGG-16,VGG-19…

进度

LeNet(1995)：2卷积+池化层，2全连接层。
AlexNet：更大更深，ReLU,Dropout，数据增强。
VGG：更大更深的AlexNet(重复的VGG块)。

总结

• VGG使用可重复使用的卷积块来构建深度卷积神经网络。
• 不同的卷积块个数和超参数可以得到不同复杂度的变种。

使用块的网络(VGG)代码实现

VGG块

import torch
from torch import nn
from d2l import torch as d2l
def vgg_block(num_convs, in_channels, out_channels):
  layers = []
  for _ in range(num_convs):
    layers.append(nn.Conv2d(in_channels, out_channels,
      kernel_size=3, padding=1))
    layers.append(nn.ReLU())
    in_channels = out_channels
  layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
  return nn.Sequential(*layers)

VGG网络

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))


def vgg(conv_arch):
  conv_blks = []
  in_channels = 1
  # 卷积层部分
  for (num_convs, out_channels) in conv_arch:
    conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
    in_channels = out_channels
  return nn.Sequential(
    *conv_blks, nn.Flatten(),
    # 全连接层部分
    nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
    nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
    nn.Linear(4096, 10))
net = vgg(conv_arch)

观察每个层输出的形状

X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
  X = blk(X)
  print(blk.__class__.__name__,'output shape:\t',X.shape)

由于VGG-11比AlexNet计算量更大，因此我们构建了一个通道数较少的网络

ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

模型训练

lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

网络中的网络(NiN)

全连接层的问题

卷积层需要较少的参数 ：C_i X C₀ X K²
但卷积层后的第一个全连接层的参数：

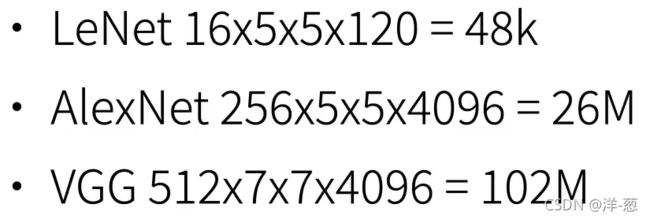
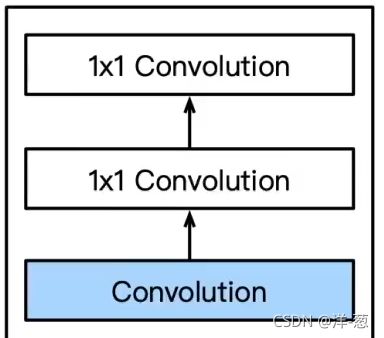
NiN块

一个卷积层后跟两个全连接层。
步长1，无填充，输出形状跟卷积层输出一样。
起到了全连接层的作用。

NiN架构

无全连接层。
交替使用NiN块和步幅为2的最大池化层。
逐步减小高宽和增大通道数。
最后使用全局平均池化层得到输出。
其输入通道数是类别数。

总结

• NiN块使用卷积层加两个1*1卷积层，后者对每个像素增加了非线性性。
• NiN使用全局平均池化层来替代VGG和AlexNet中的全连接层，不容易过拟合，更少的参数个数。

网络中的网络(NiN)代码实现

NiN块

import torch
from torch import nn
from d2l import torch as d2l
def nin_block(in_channels, out_channels, kernel_size, strides, padding):
  return nn.Sequential(
    nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
    nn.ReLU(),
    nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
    nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

NiN模型

net = nn.Sequential(
  nin_block(1, 96, kernel_size=11, strides=4, padding=0),
  nn.MaxPool2d(3, stride=2),
  nin_block(96, 256, kernel_size=5, strides=1, padding=2),
  nn.MaxPool2d(3, stride=2),
  nin_block(256, 384, kernel_size=3, strides=1, padding=1),
  nn.MaxPool2d(3, stride=2),
  nn.Dropout(0.5),
  # 标签类别数是10
  nin_block(384, 10, kernel_size=3, strides=1, padding=1),
  nn.AdaptiveAvgPool2d((1, 1)),
  # 将四维的输出转成⼆维的输出，其形状为(批量⼤⼩, 10)
  nn.Flatten())

查看每个块的输出形状

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
  X = layer(X)
  print(layer.__class__.__name__,'output shape:\t', X.shape)

训练模型

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

含并行连结的网络(GoogLeNet)

最好的卷积层超参数问题？
我们之前了解了有11的卷积核，33的卷积核，55的卷积核还有MaxPooling和AvgPooling，全连接层和多个11的卷积核，那么具体在网络中的时候我们应该如何去选择呢？

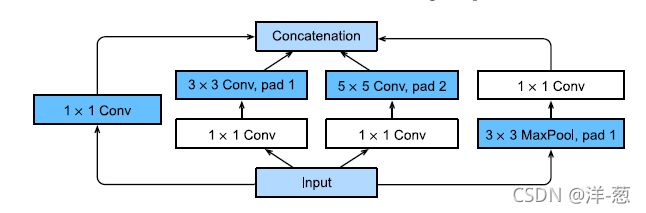
Inception块：小学生才做选择题，我全要了

4个路径从不同层面抽取信息，然后在输出通道维合并。

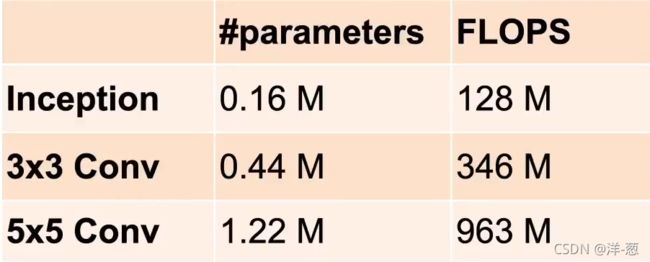
Inception块

跟单33或者55的卷积层相比，Inception块有更少的参数个数和计算复杂度。

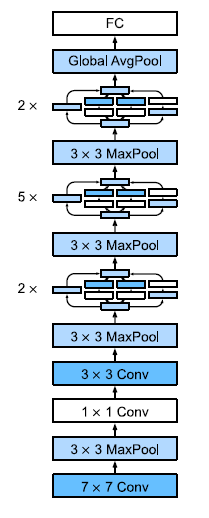
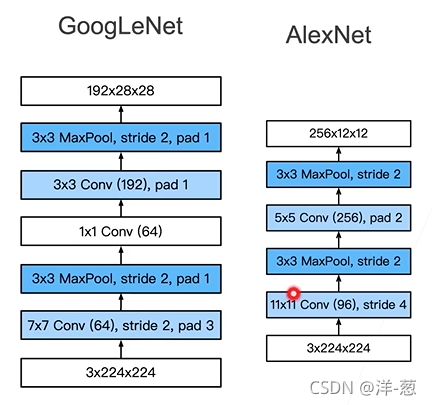
GoogLeNet总共5段，使用了9个Inception块。

段1&2

更小的宽口，更多的通道

段3

段4&5

Inception有各种后续变种

Inception-BN(v2)-使用batch normalization(后面介绍)
Inception-V3- 修改了Inception块：

• 替换55为多个33卷积层。
• 替换55为17和7*1卷积层。
• 替换33为13和3*1卷积层。
• 更深。
  Inception-V4- 使用残差连接(后面有介绍)

总结

• Inception块用4条不同超参数的卷积层和池化层的路来抽取不同的信息。它的一个主要优点是模型参数小，计算复杂度低。
• GoogleNet使用了9个Inception块，是第一个达到上百层的网络。后续有一系列改进。

GoogleNet代码实现

Inception块

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Inception(nn.Module):
  # `c1`--`c4` 是每条路径的输出通道数
  def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
    super(Inception, self).__init__(**kwargs)
    # 线路1，单1 x 1卷积层
    self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
    # 线路2，1 x 1卷积层后接3 x 3卷积层
    self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
    self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
    # 线路3，1 x 1卷积层后接5 x 5卷积层
    self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
    self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
    # 线路4，3 x 3最⼤汇聚层后接1 x 1卷积层
    self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
    self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)
  def forward(self, x):
    p1 = F.relu(self.p1_1(x))
    p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
    p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
    p4 = F.relu(self.p4_2(self.p4_1(x)))
    # 在通道维度上连结输出
    return torch.cat((p1, p2, p3, p4), dim=1)

逐一实现GoogleNet的每个模块

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
          nn.ReLU(),
          nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
          nn.ReLU(),
          nn.Conv2d(64, 192, kernel_size=3, padding=1),
          nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
          Inception(256, 128, (128, 192), (32, 96), 64),
          nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
          Inception(512, 160, (112, 224), (24, 64), 64),
          Inception(512, 128, (128, 256), (24, 64), 64),
          Inception(512, 112, (144, 288), (32, 64), 64),
          Inception(528, 256, (160, 320), (32, 128), 128),
          nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
          Inception(832, 384, (192, 384), (48, 128), 128),
          nn.AdaptiveAvgPool2d((1,1)),
          nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

为了使Fashion-MNIST上的训练短小精悍，我们将输入的高和宽从224降到96。

X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
  X = layer(X)
  print(layer.__class__.__name__,'output shape:\t', X.shape)

训练模型

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

批量归一化

损失出现在最后，后面的层训练较快。
数据在最底部：底部的层训练较慢、底部层一变化，所有都得跟着变、最后的那些层需要重新学习多次、导致收敛变慢。
我们是否可以在学习底部层的时候避免变化顶部层吗？
核心想法：
固定小批量里面的均值和方差。


可学习的参数$\gamma$和$\beta$。
作用在：

• 全连接层和卷积层输出上，激活函数前。
• 全连接层和卷积层输入上。

对全连接层，作用在特征维。
对卷积层，作用在通道维。

批量归一化在做什么？

最初论文是想用它来减少内部协变量转移。
后续有论文指出它可能就是通过在每个小批量里加入噪音来控制模型复杂度。

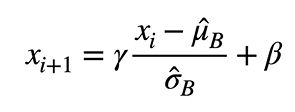
因此没必要跟丢弃法混合使用。

总结

• 批量归一化固定小批量中的均值和方差，然后学习出适合的偏移和缩放。
• 可以加速收敛速度，但一般不改变模型精度。

批量归一化的代码实现

import torch
from torch import nn
from d2l import torch as d2l
def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
  # 通过`is_grad_enabled` 来判断当前模式是训练模式还是预测模式
  if not torch.is_grad_enabled():
    # 如果是在预测模式下，直接使⽤传⼊的移动平均所得的均值和⽅差
    X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
  else:
    assert len(X.shape) in (2, 4)
    if len(X.shape) == 2:
      # 使⽤全连接层的情况，计算特征维上的均值和⽅差
      mean = X.mean(dim=0)
      var = ((X - mean) ** 2).mean(dim=0)
    else:
      # 使⽤⼆维卷积层的情况，计算通道维上（axis=1）的均值和⽅差。
      # 这⾥我们需要保持X的形状以便后⾯可以做⼴播运算
      mean = X.mean(dim=(0, 2, 3), keepdim=True)
      var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
    # 训练模式下，⽤当前的均值和⽅差做标准化
    X_hat = (X - mean) / torch.sqrt(var + eps)
    # 更新移动平均的均值和⽅差
    moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
    moving_var = momentum * moving_var + (1.0 - momentum) * var
  Y = gamma * X_hat + beta # 缩放和移位
  return Y, moving_mean.data, moving_var.data

创建一个正确的BatchNorm图层

class BatchNorm(nn.Module):
  # `num_features`：完全连接层的输出数量或卷积层的输出通道数。
  # `num_dims`：2表⽰完全连接层，4表⽰卷积层
  def __init__(self, num_features, num_dims):
    super().__init__()
    if num_dims == 2:
      shape = (1, num_features)
    else:
      shape = (1, num_features, 1, 1)
    # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
    self.gamma = nn.Parameter(torch.ones(shape))
    self.beta = nn.Parameter(torch.zeros(shape))
    # ⾮模型参数的变量初始化为0和1
    self.moving_mean = torch.zeros(shape)
    self.moving_var = torch.ones(shape)
  def forward(self, X):
    # 如果`X` 不在内存上，将`moving_mean` 和`moving_var`
    # 复制到`X` 所在显存上
    if self.moving_mean.device != X.device:
      self.moving_mean = self.moving_mean.to(X.device)
      self.moving_var = self.moving_var.to(X.device)
    # 保存更新过的`moving_mean` 和`moving_var`
    Y, self.moving_mean, self.moving_var = batch_norm(
      X, self.gamma, self.beta, self.moving_mean,
      self.moving_var, eps=1e-5, momentum=0.9)
    return Y

应用于BatchNorm于LeNet模型

net = nn.Sequential(
  nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
  nn.MaxPool2d(kernel_size=2, stride=2),
  nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
  nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
  nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
  nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
  nn.Linear(84, 10))

在Fashion-MNIST数据集上训练网络

lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

拉伸参数$\gamma$和偏移参数$\beta$

net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))

简明实现

net = nn.Sequential(
  nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6), nn.Sigmoid(),
  nn.MaxPool2d(kernel_size=2, stride=2),
  nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16), nn.Sigmoid(),
  nn.MaxPool2d(kernel_size=2, stride=2), nn.Flatten(),
  nn.Linear(256, 120), nn.BatchNorm1d(120), nn.Sigmoid(),
  nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
  nn.Linear(84, 10))

使用相同超参数来训练模型

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

ResNet

大家都在不断加深我们的网络，但是加深真的会改进精度吗？答案是不一定！

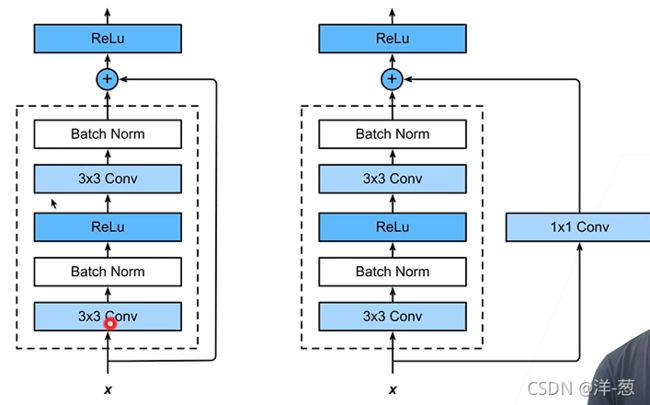
残差块

串联一个层改变函数类，我们希望能扩大函数类。
残差块加入快速通道（右边）来得到的。
f(x)=x+g(x)的结构。

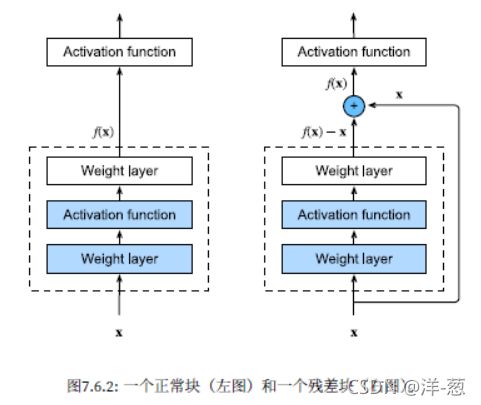
ResNet块细节

不同的残差块

ResNet块

高宽减半ResNet块（步幅2）。
后接多个高宽不变ResNet块。

ResNet架构

类似VGG和GoogleNet的总体架构，但替换成了ResNet块。

总结

• 残差块使得很深的网络更加容易训练，甚至可以训练一千层的网络。
• 残差网络对随后的深层神经网络产生了深远影响，无论是卷积类网络还是全连接类网络。

ResNet代码实现

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
class Residual(nn.Module): 
  def __init__(self, input_channels, num_channels,
        use_1x1conv=False, strides=1):
    super().__init__()
    self.conv1 = nn.Conv2d(input_channels, num_channels,
    kernel_size=3, padding=1, stride=strides)
    self.conv2 = nn.Conv2d(num_channels, num_channels,
    kernel_size=3, padding=1)
    if use_1x1conv:
      self.conv3 = nn.Conv2d(input_channels, num_channels,
      kernel_size=1, stride=strides)
    else:
      self.conv3 = None
      self.bn1 = nn.BatchNorm2d(num_channels)
      self.bn2 = nn.BatchNorm2d(num_channels)
      self.relu = nn.ReLU(inplace=True)
  def forward(self, X):
    Y = F.relu(self.bn1(self.conv1(X)))
    Y = self.bn2(self.conv2(Y))
    if self.conv3:
      X = self.conv3(X)
    Y += X
    return F.relu(Y)

输入和输出形状一致

blk = Residual(3,3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape

增加输出通道数的同时，减半输出的高和宽

blk = Residual(3,6, use_1x1conv=True, strides=2)
blk(X).shape

ResNet模型

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
      nn.BatchNorm2d(64), nn.ReLU(),
      nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

def resnet_block(input_channels, num_channels, num_residuals,
          first_block=False):
  blk = []
  for i in range(num_residuals):
    if i == 0 and not first_block:
      blk.append(Residual(input_channels, num_channels,
                use_1x1conv=True, strides=2))
    else:
      blk.append(Residual(num_channels, num_channels))
  return blk

b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

net = nn.Sequential(b1, b2, b3, b4, b5,
			nn.AdaptiveAvgPool2d((1,1)),
			nn.Flatten(), nn.Linear(512, 10))

观察一下ResNet中不同模块的输入形状是如何变化的

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
  X = layer(X)
  print(layer.__class__.__name__,'output shape:\t', X.shape)

训练模型

lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())