精英反向与二次插值改进的黏菌算法-附代码
精英反向与二次插值改进的黏菌算法
文章目录
- 精英反向与二次插值改进的黏菌算法
-
- 1.黏菌算法
- 2.改进黏菌算法
-
- 2.1 精英反向学习机制
- 2.2 二次插值方法
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.python代码
摘要:针对基本黏菌算法(Slime Mould Algorithm,SMA)易陷入局部最优值、收敛精度较低和收敛速度较慢的问题,提出精英反向学习与二次插值改进的黏菌算法(Improved Slime Mould Algorithm,ISMA)。精英反向学习策略有利于提高黏菌种群多样性和种群质量,提升算法全局寻优性能与收敛精度;利用二次插值生成新的黏菌个体,并用适应度评估更新全局最优解,有利于增强算法局部开发能力,减少算法收敛时间,使算法跳出局部极值。
1.黏菌算法
基础黏菌算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/113710762
2.改进黏菌算法
2.1 精英反向学习机制
在 2015 年, Tizhoosh [ 8 ] \operatorname{Tizhoosh}^{[8]} Tizhoosh[8] 提出了反向学习的方法 (Opposition-Based Learning, OBL), 其研究指出反向解比当 前解逼近最优解的概率高一半, 该方法可以有效增加算法种 群的多样性和质量。反向学习方法先求当前解的反向解, 再 从当前解和反向解中选取最优解且更新个体。
定义 1 反向解[9]。设在 D D D 维搜索空间中当前种群的一 个可行解为 X = ( x 1 , x 2 , … , x D ) ( x j ∈ [ a j , b j ] ) X=\left(x_1, x_2, \ldots, x_D\right)\left(x_j \in\left[a_j, b_j\right]\right) X=(x1,x2,…,xD)(xj∈[aj,bj]), 其反向解为 X ˉ = ( x 1 , ‾ , x 2 ‾ , … , x D ‾ ) \bar{X}=\left(\overline{x_1,}, \overline{x_2}, \ldots, \overline{x_D}\right) Xˉ=(x1,,x2,…,xD), 其中 x j ‾ = r ( a j + b j ) − x j , r \overline{x_j}=r\left(a_j+b_j\right)-x_j, r xj=r(aj+bj)−xj,r 是区间 [ 0 , 1 ] [0,1] [0,1] 上的随机数字。 针对反向学习存在其生成的反向解有可能比当前的搜索 空间更难搜索到最优值的问题, 精英反反向学习 (Elite Opposition-Based Learning, EOBL)被提出, 这一机制同样已经 成功应用于多种算法的优化。何庆等[10]采用 EBOL 方法初始 化种群, 增加了蜻蜓算法的种群多样性; 方旭阳等[11]引入 E B O L \mathrm{EBOL} EBOL 优化正余弦算法, 避免个体斍目地向当前学习; EBOL 机制利用精英个体相对普通个体而言携带更多有效信息的优 势, 首先通过种群中精英个体形成反向种群, 再从反向种群 和当前种群中选取优秀个体构成新的种群, EBOL 机制对增 加种群多样性和提高种群质量有良好的效果。
定义 2 精英反向解[10]。设当前种群中的普通个体的极 值点作为种群中 的精英个体 , X i , j E = ( X i , 1 E , X i , 2 E , … , X i , D E ) X_{i, j}^E=\left(X_{i, 1}^E, X_{i, 2}^E, \ldots, X_{i, D}^E\right) Xi,jE=(Xi,1E,Xi,2E,…,Xi,DE) 其反向解定义为:
KaTeX parse error: \tag works only in display equations
其中, δ \delta δ 是区间 [0,1]上的随机值, X i , j E ∈ [ l b j , u b j ] , l b j = min ( X i , j ) X_{i, j}^E \in\left[l b_j, u b_j\right], \quad l b_j=\min \left(X_{i, j}\right) Xi,jE∈[lbj,ubj],lbj=min(Xi,j), u b j = max ( X i , j ) , l b j u b_j=\max \left(X_{i, j}\right), l b_j ubj=max(Xi,j),lbj 和 u b j u b_j ubj 分别为动态边界的下界和上界, 动态 边界解决了固定边界难以保存搜索经验的问题, 有利于减少 算法的寻优时间。如果 X i , j E ‾ \overline{X_{i, j}^E} Xi,jE 超过边界, 利用随机生成的方式将 其重置, 重置方程如下:
X i , j E ‾ = rand ( l b j + u b j ) (6) \overline{X_{i, j}^E}=\operatorname{rand}\left(l b_j+u b_j\right)\tag{6} Xi,jE=rand(lbj+ubj)(6)
2.2 二次插值方法
二次揷值(Quadratic Interpolation, QI)是一种局部搜索算 子, 它使用曲线来拟合二次函数的形状, 以获得的曲线极值 点近似函数最优解。这种局部搜索方法对优化算法有较大的 参考价值, 已经成功应用于多种算法的优化。Sun 等人 [ 12 ] { }^{[12]} [12] 提 出了二次揷值改进的鲸鱼优化算法, 廖列法等人 [ 13 ] { }^{[13]} [13] 提出二次 揷值改进的天牛须算法, 王秋萍等人 [ 14 ] { }^{[14]} [14] 提出了二次揷值改进 的飞蛾火焰算法; 实验结果表明, 二次揷值作为局部搜索算 子应用到元启发算法中, 可以有效地增强所应用算法的局部 搜索能力。
假设 X X X 和 Y Y Y 是 D D D 维问题中种群的两个随机位置, 其中, X = ( x 1 , x 2 , … , x D ) , Y = ( y 1 , y 2 , … , y D ) X=\left(x_1, x_2, \ldots, x_D\right) , Y=\left(y_1, y_2, \ldots, y_D\right) X=(x1,x2,…,xD),Y=(y1,y2,…,yD), 当前全局最优位置为 Z = ( z 1 , z 2 , … , z D ) , X 、 Y 、 Z Z=\left(z_1, z_2, \ldots, z_D\right), X 、 Y 、 Z Z=(z1,z2,…,zD),X、Y、Z 的适应度值分别 F ( X ) 、 F ( Y ) 、 F ( Z ) F(X) 、 F(Y) 、 F(Z) F(X)、F(Y)、F(Z), 则二次揷值方法根 据以下公式更新位置形成新个体 X ˉ = ( x 1 ‾ , x 2 ‾ , … , x D ‾ ) \bar{X}=\left(\overline{x_1}, \overline{x_2}, \ldots, \overline{x_D}\right) Xˉ=(x1,x2,…,xD) :
x q = ( z q 2 − y q 2 ) × F ( X ) + ( x q 2 − z q 2 ) × F ( Y ) + ( y q 2 − x q 2 ) × F ( Z ) 2 [ ( z q − y q ) × F ( X ) + ( x q − z q ) × F ( Y ) + ( y q − x q ) × F ( Z ) ] (7) x_q=\frac{\left(z_q^2-y_q^2\right) \times F(X)+\left(x_q^2-z_q^2\right) \times F(Y)+\left(y_q^2-x_q^2\right) \times F(Z)}{2\left[\left(z_q-y_q\right) \times F(X)+\left(x_q-z_q\right) \times F(Y)+\left(y_q-x_q\right) \times F(Z)\right]} \tag{7} xq=2[(zq−yq)×F(X)+(xq−zq)×F(Y)+(yq−xq)×F(Z)](zq2−yq2)×F(X)+(xq2−zq2)×F(Y)+(yq2−xq2)×F(Z)(7)
其中 q = 1 , 2 , … , D q=1,2, \ldots, D q=1,2,…,D 。
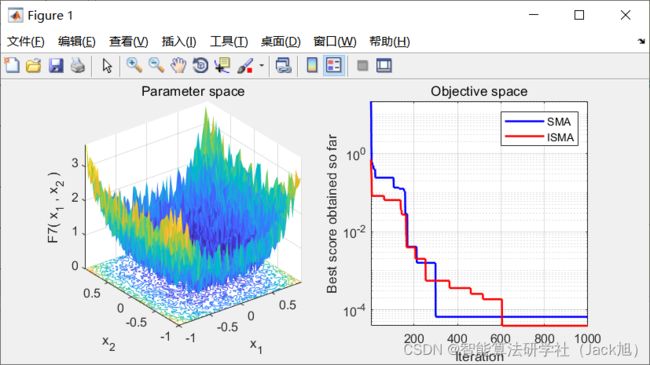
3.实验结果
4.参考文献
[1]郭雨鑫,刘升,张磊,黄倩.精英反向与二次插值改进的黏菌算法[J/OL].计算机应用研究:1-7[2021-11-10].https://doi.org/10.19734/j.issn.1001-3695.2021.02.0175.