CSP-J 2021 插入排序(详细思路)
题目描述:
插入排序是一种非常常见且简单的排序算法。小 Z 是一名大一的新生,今天 H 老师刚刚在上课的时候讲了插入排序算法。
假设比较两个元素的时间为 O(1),则插入排序可以以 O(n*n) 的时间复杂度完成长度为 n 的数组的排序。不妨假设这 n 个数字分别存储在 a1,a2,··· ,an 之中,则如下伪代码给出了插入排序算法的一种最简单的实现方式:这下面是 C/C++ 的示范代码。
for(int i=1;i<=n;i++)
{
for(int j=i;j>=2;j--){
if(a[j]<a[j-1]){
int t=a[j-1];
a[j-1]=a[j];
a[j]=t;
}
}
}
为了帮助小 Z 更好的理解插入排序,小 Z 的老师 H 老师留下了这么一道家庭作业:
H 老师给了一个长度为 n 的数组 a,数组下标从 1 开始,并且数组中的所有元素均为非负整数。小 Z 需要支持在数组 a 上的 Q 次操作,操作共两种,参数分别如下:
1 x v : 这是第一种操作,会将 a 的第 x 个元素,也就是 ax 的值,修改为 v。保证1 ≤ x ≤ n,1 ≤ v ≤ 10^9。注意这种操作会改变数组的元素,修改得到的数组会被保留,也会影响后续的操作。
2 x : 这是第二种操作,假设 H 老师按照上面的伪代码对 a 数组进行排序,你需要告诉 H 老师原来 a 的第 x 个元素,也就是 ax,在排序后的新数组所处的位置。保证 1 ≤ x ≤ n。注. 意. 这种操作不会改变数组的元素,排序后的数组不会被保留,也不会影后续的操作。
H 老师不喜欢过多的修改,所以他保证类型 1 的操作次数不超过 5000。
小 Z 没有学过计算机竞赛,因此小 Z 并不会做这道题。他找到了你来帮助他解决这个问题。
**输入:**输入的第一行包含两个正整数 n,Q,表示数组长度和操作次数。保证 1 ≤ n ≤8,000,1 ≤ Q ≤ 2 × 10^5。
输入的第二行包含 n 个空格分隔的非负整数,其中第 i 个非负整数表示 ai。保证1 ≤ ai ≤ 10^9。
接下来 Q 行,每行 2 ∼ 3 个正整数,表示一次操作,操作格式见题目描述。
**输出:**对于每一次类型为2的询问,输出一行一个正整数表示答案。
样例输入:
3 4
3 2 1
2 3
1 3 2
2 2
2 3
样例输出:
1
1
2
提示:
【样例1解释】
在修改操作之前,假设 H 老师进行了一次插入排序,则原序列的三个元素在排序结束后所处的位置分别是 3,2,1。
在修改操作之前,假设 H 老师进行了一次插入排序,则原序列的三个元素在排序结束后所处的位置分别是 3,1,2。
注意虽然此时 a2 = a3,但是我们不能将其视为相同的元素。
【数据范围】
对于所有测试数据,满足1 ≤ n ≤ 8,000,1 ≤ Q ≤ 2×10^5,
1 ≤ x ≤ n, 1 ≤ v,ai ≤ 10^9。
对于所有测试数据,保证在所有 Q 次操作中,至多有 5000 次操作属于类型一。
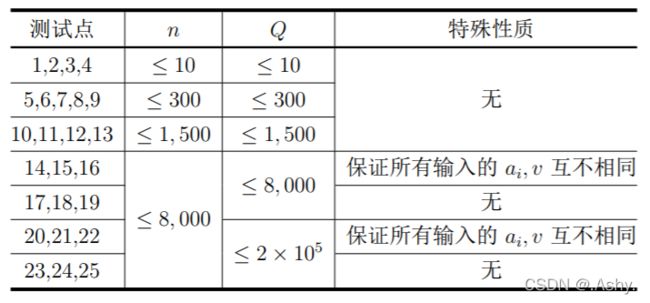
各测试点的附加限制及分值如下表所示。
思路:
两种操作:
1.修改序列中的值
2.查找排序后的位置
修改序列中的值可以通过O(1)的时间复杂度解决,而求排序后的这个数的位置,我们可以通过一个小公式求出:
这个数排序后的位置=所有的数中比其小的数+他前面和他相等的的数+1;
因为在样例一解释中相同的数视为不同的元素所以要加上所求数前面和他相等的数;
例如:
3 2 2
求 第三个元素 排序后的位置
根据公式就是:0+1+1=2
排序后的位置就是2,这个例子就是样例的最后一组查询;
知道了如何查找位置后我们简单的看一下查找位置的复杂度为O(n);
根据之前的推导,我们先写出一种解法
#include我第一次做的很急,没来得及算复杂度,然后TLE了,我们算一下这个程序的最坏复杂度:
最大查询次数为2×10^5次,每次复杂度为O(n),最大为8000,最坏复杂度就是
1.6×10^9 果然爆了;
优化:
H 老师不喜欢过多的修改,所以他保证类型 1 的操作次数不超过 5000。
这句话很重要,优化思路就是以这句话想出来的;
优化思路就是修改次数这么少,我们不如做一个预处理,然后每次查询直接输出,每次修改的时候再处理O(n)的遍历;
每次查找位置的复杂度为O(1)
而每次修改的复杂度为O(n)(这里的复杂度一会给出解释)
最坏复杂度大概是8000×8000(预处理)+5000×8000(修改)+(200000-5000)*1 大约是 1e8的复杂度,优化了一个数量级;下面给出代码
#include
for(int i=1;i<=q;i++)
{
cnt1=0;cnt2=0;
scanf("%d",&k);
if(k==1)
{
scanf("%d %d",&k1,&k2);
cc(k1,k2);//修改
// for(int i=1;i<=n;i++)
// cout<
}
else if(k==2)
{
scanf("%d",&k1);
printf("%d\n",all1[k1]+left1[k1]+1);//查询
}
}
}
在修改的时候,程序会变得难写不少,因为当一个点发生变化,所有预处理的值都会受到影响,但是我们也要尝试来模拟修改,当一个点发生变化的时候
1.这个点的两个属性都会发生改变
2.这个点左右所有的点(比其小)这个属性会发生改变
3.这个点右边的点(左边和其相等这个属性)会发生改变
而这些属性的改变只要一个循环就能全部求出
只要每个点都遍历一遍
减去修改前点的影响再加上新点的影响即可
因此复杂度也是O(n);
这题写出来的时候开心到不行,第一次做出我觉得有难度的一个题,也许这就是解题的快了吧;
加油!