深度学习修炼（六）——神经网络分类问题

6 分类任务

在这一讲中，我们打算探讨一下神经网络中是如何处理分类任务的。

6.1 前置知识

6.1.1 分类

如果只是二分分类，这种分类我们大可只用0或者1来表示，那么我们只需要采用sigmoid函数来修正为0或1即可（如果不懂后面会重新讲sigmoid函数），那如果是多种可能呢？

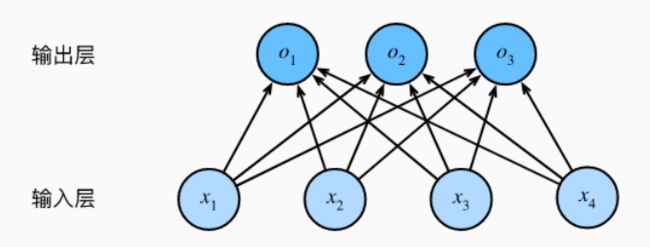
假设每次输入是一个2×2的灰度图像。我们可以用一个标量表示每个像素值，每个图像对应四个特征$x_1,x_2,x_3,x_4$，此外，假设每个图像属于类别"猫",“鸡”,"狗"中的一个。

接下来，我们要选择如何表示标签，如同我们前面所说，我们肯定不可能说P = “猫”,我们有两个明显地选择：最直接的想法是选择y∈{1,2,3}，其中正数分别代表{“狗”,“猫”,“鸡”}。

但是统计学家很早之前就发明了一种表示分类数据的简单方法：独热编码。独热编码是一个向量，它的分量和类别一样多。类别对应的分量设置为1，其他所有分量设置为0。比如说应用到我们这个例子上的话，我们就可以用独热编码来表示我们的标签y，其中猫对应(1,0,0)，鸡对应(0,1,0)，狗对应(0,0,1)。

6.1.2 分类的网络

在神经网络中，我们通常使用softmax回归来进行分类任务。

在分类任务重，我们本质上是在算这个图片是不是某一类的概率，这个概率是要多大才能判定这个图片属于这个类？这个概率要达到什么标准？这个标准是我们自己定的，也就是所谓的阈值。

我们希望把我们通过运算算出来的${\hat{y}}_j$可以直接看做是类别j的概率，但是这明显不可能，因为我们知道概率是处于0到1的，我们又没对这个模型做什么处理，他凭什么输出的值刚好就在0和1之间，是吧。

那么既然没有处理，那接下来就要让输出结果某种处理后，变成0-1之间，这个处理我们就叫做校准。那我们要用什么东西来校准呢？softmax函数。softmax函数可以将未规范化的预测变换为非负并且总和为1，同时要求模型保持可导。其函数形式为：$\hat{y}=softmax(o),其中{\hat{y}}_i=\frac{exp(o_j)}{{\sum }_{k}exp(o_k)}$。

这里，对于所有的j总有0<=$\widehat{y_j}$<=1。因此，$\hat{y}$可以视为一个正确的概率发布。softmax运算不会改变未规范化的预测o之间的顺序，只会确定分配给每个类别的概率。

从上面的公式我们可以看出，这个公式明显不是线性函数，但是由于我们是先通过输入特征的仿射变换做出o，然后再把o出入上面的softmax函数中的，所以，softmax回归是一个线性模型。

6.2 动手

或许前置的知识再多也是花里胡哨。让我们试着动手搭建一个神经网络来进行分类。不过，我们这一小节的目的是为了熟悉nn.Module模块和nn.functional模块。

6.2.1 读取数据

让我们先读取数据，这里我们暂时不使用前面学过的torch.datasets和torch.utils.data.DataLoader。如果你不是很懂下面的读取数据的代码，没关系，这看得懂看不懂都不是我们学习的重点。你照做即可。

%matplotlib inline

from pathlib import Path
import requests

DATA_PATH = Path("data")
PATH = DATA_PATH / "mnist"

PATH.mkdir(parents=True, exist_ok=True)

URL = "http://deeplearning.net/data/mnist/"
FILENAME = "mnist.pkl.gz"

if not (PATH / FILENAME).exists():
        content = requests.get(URL + FILENAME).content
        (PATH / FILENAME).open("wb").write(content)
  
import pickle
import gzip

with gzip.open((PATH / FILENAME).as_posix(), "rb") as f:
        ((x_train, y_train), (x_valid, y_valid), _) = pickle.load(f, encoding="latin-1")

from matplotlib import pyplot
import numpy as np

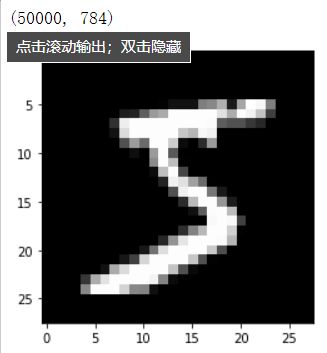
pyplot.imshow(x_train[0].reshape((28, 28)), cmap="gray")
print(x_train.shape)

out：

对于分类任务不像回归，它的输出并不是1，而是类别数。

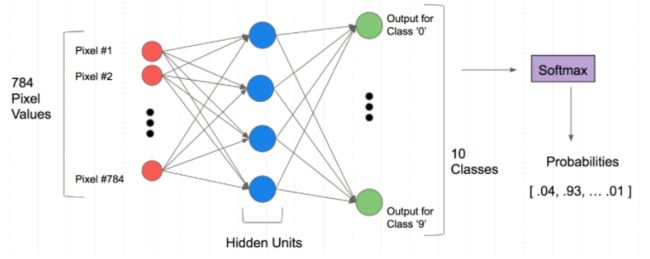
如果我们要将某样本归为十个类中的一个，那么输出结果就是对应类的独热编码，也就是向量中有10个数字。

举个例子，如果我们输入的样本是1×784，那么我可以在第二层将变为784×128，输出层变为128×10，然后输出的10个值再交由softmax回归将其每个数的范围降到0-1，然后看其属于哪个类别的数字大即属于哪个类别。

6.2.2 functional模块

functional模块有的实际上Module都有，但是在调用一些不涉及参数的例如不涉及w和b的方法时，推荐使用functional。

如，继续上面的例子，我们先将数据分为训练集和测试集，然后将数据转为张量：

import torch

x_train, y_train, x_valid, y_valid = map(
    torch.tensor, (x_train, y_train, x_valid, y_valid)
)
n, c = x_train.shape
x_train, x_train.shape, y_train.min(), y_train.max()
print(x_train, y_train)
print(x_train.shape)
print(y_train.min(), y_train.max())

我们利用functional模块来搭建一个线性回归模型试试：

import torch.nn.functional as F

# 指定损失函数为交叉熵
loss_func = F.cross_entropy

# 定义模型
def model(xb):
    return xb.mm(weights) + bias

交叉熵实际上就是对数似然损失函数，这个知识点我们在机器学习的练功方式（十一）——逻辑回归_弄鹊的博客-CSDN博客已经提过了，忘记的可以去复习一下。

# 定义小批量随机梯度下降每次取多少样本
bs = 64
xb = x_train[0:bs]  # a mini-batch from x
yb = y_train[0:bs]
# 初始化随机参数
weights = torch.randn([784, 10], dtype = torch.float,  requires_grad = True) 
bias = torch.zeros(10, requires_grad=True)

# 打印损失值
print(loss_func(model(xb), yb))

6.2.3 继续搭建分类神经网络

让我们继续以上的工作。我们利用nn.Module来搭建一个softmax回归分类器。

from torch import nn

class Mnist_NN(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden1 = nn.Linear(784, 128)
        self.hidden2 = nn.Linear(128, 256)
        self.out  = nn.Linear(256, 10)

    def forward(self, x):
        x = F.relu(self.hidden1(x))
        x = F.relu(self.hidden2(x))
        x = self.out(x)
        return x

在前面第三讲的时候我们忘记提到的一点是：在利用torch框架搭建神经网络时，无需自己去写一个反向传播，只需写好正向传播即可，对于反向传播torch框架内部已经提供给我们了。

在以上搭建的神经网络中，我们在__ init __()方法中先写好了神经网络的每个层，然后在forward()方法中，我们让x首先输入到第一层中，输出的结果用F中的relu激活函数激活一下再流往下一层。第二层同理，得出的结果也是再次使用relu激活函数激活，然后最终通过输出层输出。

定义好之后，我们需要实例化该神经网络类：

net = Mnist_NN()
print(net)

out：

Mnist_NN(
(hidden1): Linear(in_features=784, out_features=128, bias=True)
(hidden2): Linear(in_features=128, out_features=256, bias=True)
(out): Linear(in_features=256, out_features=10, bias=True)
)

对于net对象，实际上torch为其写好了内置方法net_parameters，其依次返回name,parameter。

#可以打印我们定义好名字里的权重和偏置项

for name, parameter in net.named_parameters():
    print(name, parameter,parameter.size())

out：

6.2.4 继续简化

我们可以利用TensorDataset和DataLoader来继续简化上述的过程。

在前面我们学过，我们小批量随机梯度下降。其简单来说就是取小批量的数据，然后取其损失的均值来代替全局损失。在第二讲我们学过DataLoader，它可以用于每次从总数据中每次抽取batch_size的数据。

而对于TensorDataset，它可以将传入的数据张量转换为torch可识别的dataset格式类型的数据，从而方便让DataLoader处理。

让我们看一下以下的代码：

from torch.utils.data import TensorDataset
from torch.utils.data import DataLoader

# 转换DataLoader可处理的类型并且批量提取数据
train_ds = TensorDataset(x_train, y_train)
train_dl = DataLoader(train_ds, batch_size=bs, shuffle=True)

valid_ds = TensorDataset(x_valid, y_valid)
valid_dl = DataLoader(valid_ds, batch_size=bs * 2)

def get_data(train_ds, valid_ds, bs):
    return (
        DataLoader(train_ds, batch_size=bs, shuffle=True),
        DataLoader(valid_ds, batch_size=bs * 2),
    )

6.2.5 训练模型

一般在训练模型时，我们都会加上model.train()方法，这样模型在训练时会自动加入Bathc Normalization(批量归一化)和Dropout(暂退法)，防止过拟合。而在测试模型时，我们一般加上model.eval()方法，这样就不会调用归一化和暂退法。

Dropout下一小节就讲了，这里只要知道它是防止过拟合的即可。

让我们看一下下面的代码：

def loss_batch(model, loss_func, xb, yb, opt=None):
    # 计算损失值
    loss = loss_func(model(xb), yb)

    # 如果优化器不为空
    if opt is not None:
        # 执行反向传播
        loss.backward()
        # 更新参数
        opt.step()
        # 梯度清零
        opt.zero_grad()

    # 返回损失总值，和批量x的长度
    return loss.item(), len(xb)

然后训练：

import numpy as np

def fit(steps, model, loss_func, opt, train_dl, valid_dl):
    for step in range(steps):
        model.train()
        for xb, yb in train_dl:
            loss_batch(model, loss_func, xb, yb, opt)

        model.eval()
        with torch.no_grad():
            losses, nums = zip(
                *[loss_batch(model, loss_func, xb, yb) for xb, yb in valid_dl]
            )
        val_loss = np.sum(np.multiply(losses, nums)) / np.sum(nums)
        print('当前step:'+str(step), '验证集损失：'+str(val_loss))

指定优化器：

from torch import optim
def get_model():
    model = Mnist_NN()
    return model, optim.SGD(model.parameters(), lr=0.001)

调用上面所有写的函数即可：

# 对总数据进行分批量
train_dl, valid_dl = get_data(train_ds, valid_ds, bs)
# 拿到模型和优化器
model, opt = get_model()
# 开始训练
fit(25, model, loss_func, opt, train_dl, valid_dl)

out：

[{“metadata”:{“trusted”:true},“cell_type”:“code”,“source”:"# 对总数据进行分批量\ntrain_dl, valid_dl = get_data(train_ds, valid_ds, bs)\n# 拿到模型和优化器\nmodel, opt = get_model()\n# 开始训练\nfit(25, model, loss_func, opt, train_dl, valid_dl)",“execution_count”:null,“outputs”:[{“output_type”:“stream”,“text”:“当前step:0 验证集损失：2.27946646194458\n当前step:1 验证集损失：2.2453414649963377\n当前step:2 验证集损失：2.1901785594940186\n当前step:3 验证集损失：2.0985936725616456\n当前step:4 验证集损失：1.9537098587036132\n当前step:5 验证集损失：1.749969289779663\n当前step:6 验证集损失：1.4996562250137329\n当前step:7 验证集损失：1.2475741912841798\n当前step:8 验证集损失：1.041046302986145\n当前step:9 验证集损失：0.8889363418579102\n当前step:10 验证集损失：0.7784037446022034\n当前step:11 验证集损失：0.6955419854164123\n当前step:12 验证集损失：0.6328013188362122\n当前step:13 验证集损失：0.5834899019241333\n当前step:14 验证集损失：0.5442861658096313\n当前step:15 验证集损失：0.5122919623851776\n当前step:16 验证集损失：0.4864934079647064\n当前step:17 验证集损失：0.46465890626907347\n当前step:18 验证集损失：0.4461087041854858\n当前step:19 验证集损失：0.4306937822341919\n当前step:20 验证集损失：0.4172893476009369\n当前step:21 验证集损失：0.40593954257965087\n”,“name”:“stdout”}]}]

6.3 暂退法

在前一小节中我们提到了dropout暂退法。在这一小节中，我们来着重谈论一下。

6.3.1 重新看待过拟合问题

当面对更多的特征而样本不足时，线性模型往往会过拟合。相反，当给出更多的样本而不是特征，通常线性模型不会过拟合。不幸的是，线性模型泛化的可靠性是由代价的。简单地说，线性模型没有考虑到特征之间的交互作用。对于每个特征，线性模型都必须指定正的或负的权重。

泛化小和灵活性之间的这种基本权衡被描述为偏差——方差权衡。线性模型有很高的偏差：它们只能表示一小类函数。然而，这些模型的方差很低：它们在不同的随机数据样本上可以得出了相似的结果。

如果把偏差——方差看成一个色谱，那么与之相反的一端的是深度神经网络。神经网络并不局限与单独查看每个特征，而是学习特征之间的交互。例如：神经网络可能推断“尼日利亚”和“西联汇款”一起出现在电子邮件中表示垃圾邮件，但单独出现则不表示垃圾邮件。

即使我们有比特征多得多的样本，深度神经网络也有可能过拟合。

6.3.2 在稳健性中加入扰动

在探究泛化性之前，我们先来定义一个什么是一个“好”的预测模型。前面我们说过，我们希望训练误差和泛化误差之间折中，做到一个模型能够很好地拟合训练数据，也能够很好地预测未知数据。所以根据经典泛化理论 ：为了缩小训练和测试性能之间的差距，应该以简单的模型为目标。简单些以较小维度的形式展现。这也是为什么开头我们用了最简单的线性模型来讲解原理的缘故。而正则化也是一样，为了说明我们是要减少特征向量的大小，我们直接对特征向量大小对应的概念——范数来下手。

简单性的另一个角度是平滑性。即函数不应该对其输入的微小变化敏感(这个也叫鲁棒性)。这也是为什么我们第一章线性模型所需的数据中我们往里添加了噪声点。因为一个好的模型不应该因为某些微小的噪声就失效。

所以根据上面所说的原理，科学家提出了一个想法：在训练过程中，在进行后续层的计算（我们的计算比如第一层输入层是不计算的，主要的计算在第二层）之前，我们先对网络添加小部分噪声。因为当训练一个有多层的深层网络时，注入噪声只会在输入——输出映射上增强平滑性。

这个想法被称为暂退法也叫丢弃法。暂退法在前向传播的过程中，计算每一内部层的同时注入噪声，这已经称为训练神经网络的常用技术。这种方法之所以被称为暂退法，是因为我们从表面上看是在训练的过程中丢弃一些神经元。在整个训练过程的每一次迭代中，标准暂退法包括在计算下一层之前将当前层中的一些结点置零。

6.3.3 暂退法实际的实现

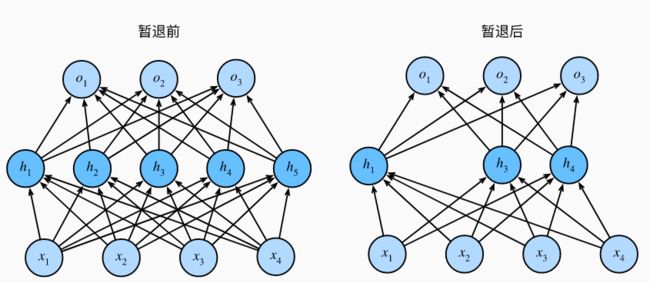
回想之前做的多层感知机。如果我们将暂退法应用到隐藏层，以p的概率将隐藏单元置为零时，结果可以看作是只包含原始神经元子集的网络。比如在下图中，删除了h2和h5，因此输出的计算不再依赖于h2和h5，并且它们各自的梯度在执行反向传播时也会消失。这样，输出层的计算不能过度依赖于h1-h5的任何一个元素。

通常，我们在测试的时候不会用到暂退法。给定一个训练好的模型和一个新的样本，我们不会丢弃任何节点，因此不需要标准化。但是研究人员就需要去用暂退法去估计神经网络预测的不确定性了；如果通过应用不同暂退法（一种暂退法包含抹去某些节点）得到的预测结果都是一致的，那么我们可以说网络发挥更稳定。

6.4 后话

我知道，这一小节你学的很不愉快。实际上，太多细致的知识无法在一个小节中直接说完，所以请不要紧张，这里即使你不懂太多的东西，你只要会一个就行了——搭建个网络，即使不会训练也没有关系，先会搭网络就足够了。在后面的学习中你会发现，除了搭网络这个地方不一样，实际上训练的过程都是一样的。