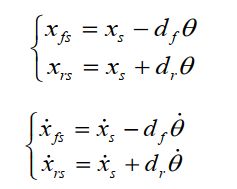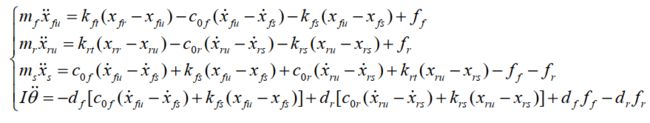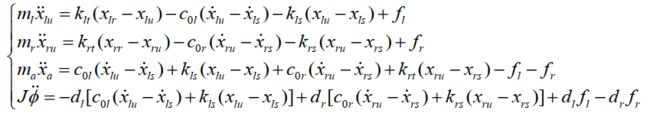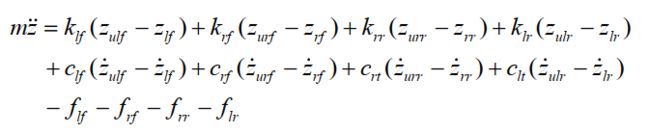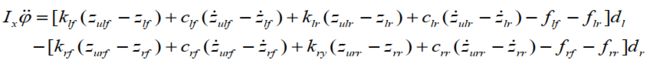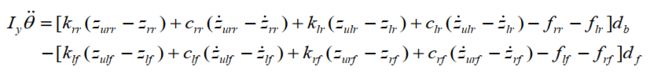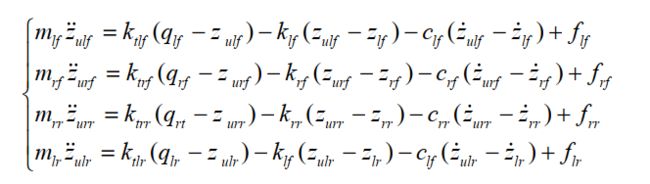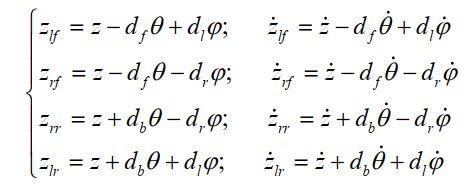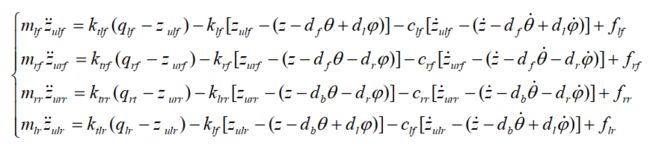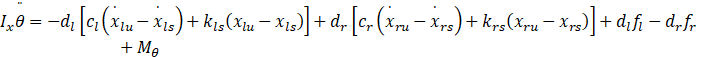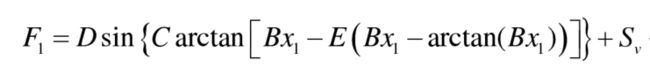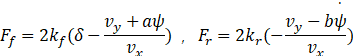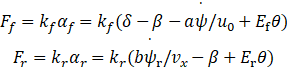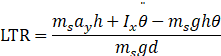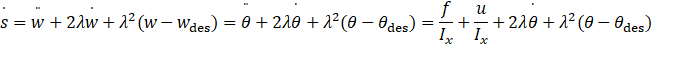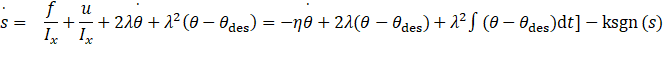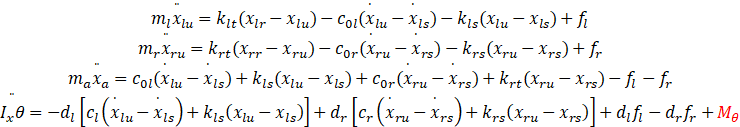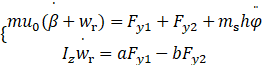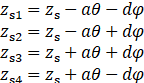半车(前后、左右)、整车悬架详细推导建模和simulink仿真分析
目录
前言
1.前后(Pitch)半车主动悬架模型
1.1 simulink前后半车悬架建模
1.1.2 搭积木法建模
1.1.3 S-Function建模(被动悬架为例)
1.2 仿真结果
2.左右(Roll)半车悬架模型(不含转向)
2.1 Simulink模型
2.2 仿真结果
3.整车悬架模型(不含转向)
3.1 整车7自由度主动悬架数学模型
3.2 Simulink建模
3.3 仿真结果
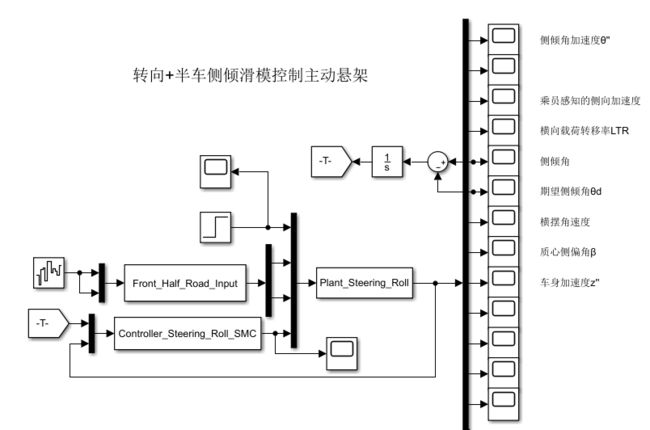
4.转向 +半车侧倾悬架(6自由度)模型
4.1 转型+侧倾数学模型
4.1.1侧向运动
4.1.2横摆运动
4.1.3 因转向带来的侧倾力矩
4.2 轮胎模型
4.3 横向载荷转移率
4.4确定期望的侧倾角
4.5 simulink仿真分析
4.5.1 考虑相干性、延迟性的整车随机路面激励
4.5.2 2自由度转向+4自由度半车侧倾模型
4.5.3 2自由度转向+4自由度半车侧倾模型(被动)仿真结果
4.5.3滑模控制器设计
编辑 4.5.4 转向+半车侧倾悬架滑模控制仿真
4.5.5 2自由度转向+4自由度半车侧倾滑模控制主动悬架仿真结果
5.侧倾力矩+侧倾4自由度模型(不建议)
5.1 仿真分析
6.转向 +半车俯仰悬架(6自由度)模型
6.1仿真结果
7.转向 +整车悬架(9自由度)模型
7.1模型自由度计算
7.2转向工况下的整车数学模型推导
7.2.1 转向运动方程
7.2.2 侧倾运动方程
7.2.3 俯仰运动方程
7.2.4 车身垂向运动方程
7.2.5 车身垂向运动方程
7.2.6轮胎侧偏力
7.3 状态变量和输入选取
7.3.1状态变量
7.3.2扰动输入
7.3.3控制输入
7.4Simulink模型
7.5 仿真结果
前言
半车悬架模型分为前后半车悬架模型(垂向+俯仰运动)、左右半车悬架模型(垂向+侧倾运动)两种,这里它们分别都是4自由度;如果研究抗侧倾时加上转向模型(侧向+横摆运动或者合起来说横向运动)2自由度,则是半车+转向的6自由度抗侧倾模型。
整车模型如果不加转向是7自由度模型,如果加上转向,则构成9自由度模型。
假设条件:一般是做对称、俯仰角和侧倾角很小等理想条件。
对于线性二自由度模型(转向系统)的详细数学模型和simulink建模可以参考我的这篇文章:
线性二自由度模型建立及simulink仿真分析_Mr. 邹的博客-CSDN博客
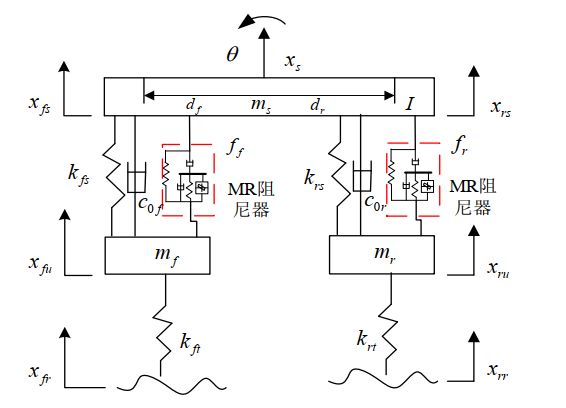
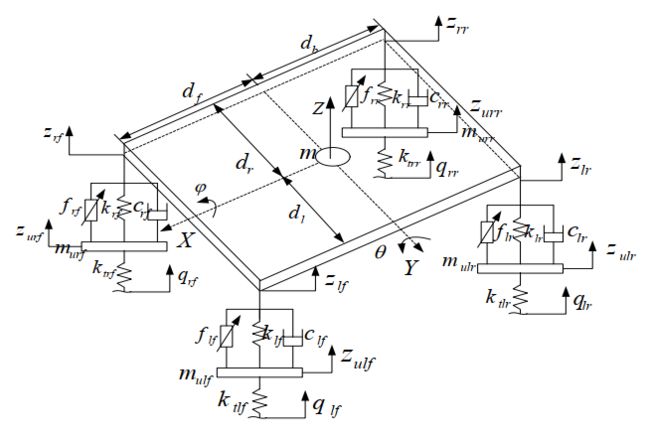
1.前后(Pitch)半车主动悬架模型
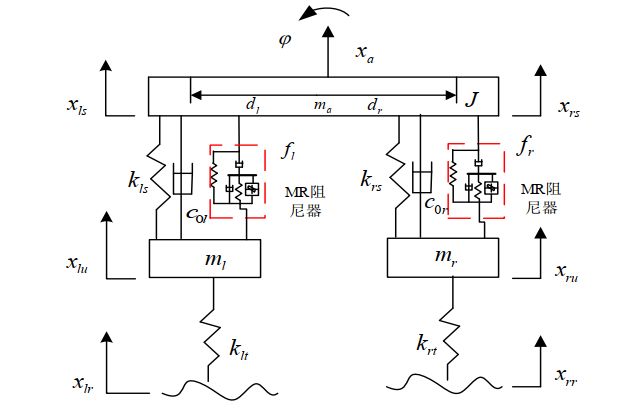
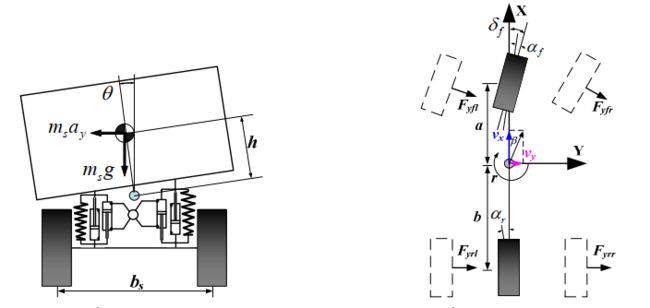
以主动悬架为例,被动悬架即主动控制力=0即可,数学模型如下:
其中, ms、 xs、 xfs、 xrs 分别为簧载质量及其质心、 前端、后端的垂向位移; mf、 xfu 分别为前悬架非簧载质量及其垂向位移; mr、 xru 分别为后悬架非簧载质量及其垂向位移; θ为俯仰角, I 为转动惯量; kfs、 c0f 分别为前悬架的弹簧刚度和不可调阻尼系数; krs、 c0r 分别为后悬架的弹簧刚度和不可调阻尼系数; kft、 krt 分别为前、 后轮胎刚度; ff、 fr 分别为前、后悬架的可调阻尼力; xfr、 xrr 分别为前、 后轮路面激励; df、 dr 分别为前、 后轮到质心的距离。
假设俯仰角很小θ,车身的绝对位移和速度近似为:
所以前后轮四自由度 1/2 车半主动悬架系统的动力学方程可表示为:
注:实际上俯仰角用φ表示,侧倾角用θ表示更常见,但是这里文献用这个,我为了方便表示就用这个吧,后面的不同模型是综合几个文献给出来的,具体参数表达的含义可能变动,所以读者可以通过给定的模型手里分析图片进行建模考虑。
1.1 simulink前后半车悬架建模
simulink模型方法总结:
①从simulink出发,建模方法有两种:搭积木法和函数编写,其中搭积木法比较繁琐,但是简单;函数编写法可以使用matlab fcn或者s-Function等模块,个人认为s-Function编写较简捷。
②从数学基础出发,建模可以用微分方程着手建立,还可以用状态空间表达式建立,但是两者的本质其实类似,都需要先找好状态变量(状态变量选取不唯一)。个人理解状态变量个数=系统微分方程的总阶数(欢迎指正)[现代控制理论1-1] 状态方程的建立 - 知乎
这里选取前后车身的位移和速度、前后车轮的位移和速度,这8个变量为状态变量,即:
![]()
篇幅原因,状态空间方程这里不进行叙述,有兴趣读者可以查看相关文献或者自行推导。
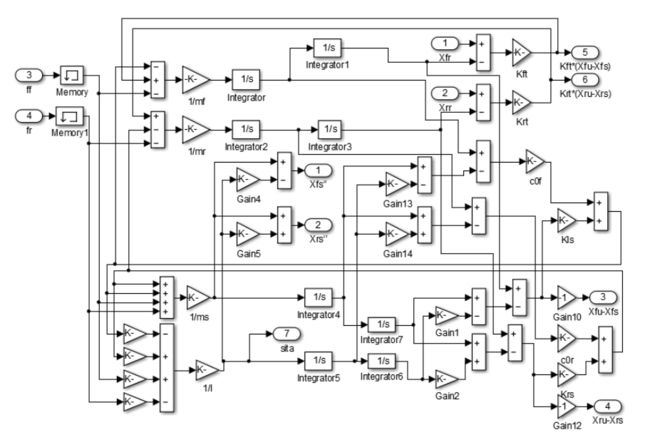
1.1.2 搭积木法建模
1.1.3 S-Function建模(被动悬架为例)
1.2 仿真结果
2.左右(Roll)半车悬架模型(不含转向)
2.1 Simulink模型
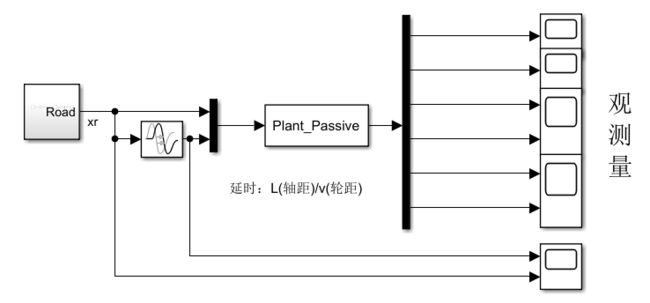
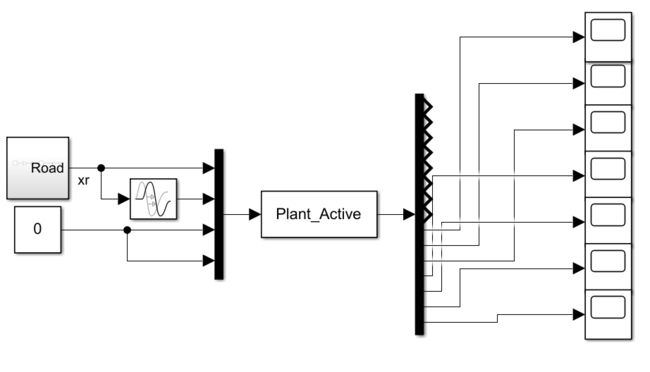
这里仍以被动悬架为例(模型为主动悬架,但是我给的是0控制输入,模型是被动),模型如下:
注:此处路面输入未考虑左右轮相关性。
2.2 仿真结果
注:观测变量可以按需选择,这里我的模型是好早前建立的,所以直接运行结果记录在这里,没有去调整。
3.整车悬架模型(不含转向)
3.1 整车7自由度主动悬架数学模型
簧载垂向运动方程:
俯仰运动方程为:
非簧载质量垂向运动方程为:
做出俯仰角θ和侧倾角φ很小的假设,所以有如下近似条件:
整理汇总得:
3.2 Simulink建模
以被动悬架进行分析(即上面的主动悬架模型的控制力=0),为了节省篇幅,这里观测变量只输出3个。
3.3 仿真结果
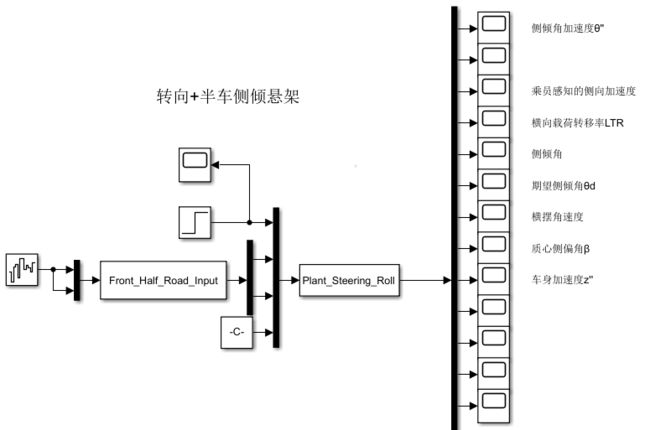
4.转向 +半车侧倾悬架(6自由度)模型
4.1 转型+侧倾数学模型
侧倾模型 侧向+横摆模型(转向模型)
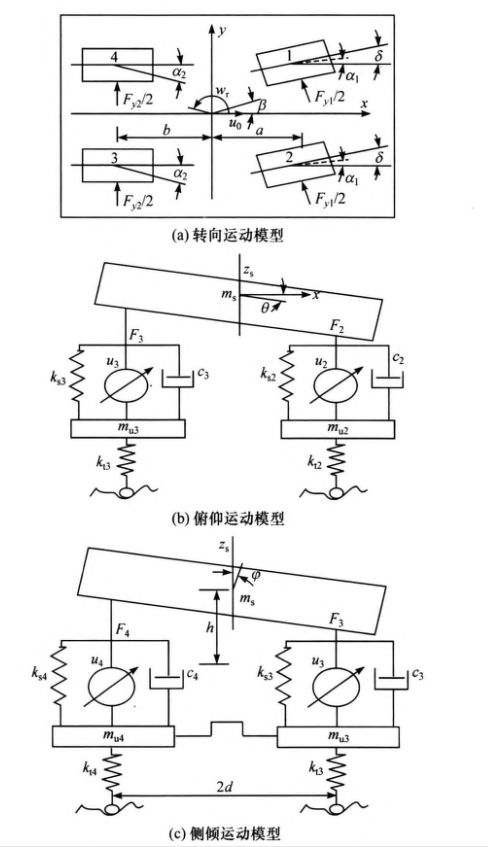
转向模型或者说线性二自由度车辆操纵动力学模型,它主要反映模型水平方向运动(即在水平面的运动)。转向系统对模型的影响不作考虑,并且将前轮转角δ作为控制系统的输入;不考虑悬架子系统的作用,认为模型沿 z 轴位移,绕 y 轴俯仰角和绕 x 轴侧倾角均为零,只考虑模型沿 y 轴的侧向运动与绕 z 轴的横摆运动。此外,轮胎侧偏的角度满足小角度假设(即可以忽略或者三角函数等于角度本身),车轮的侧偏刚度处于线性范围之内。
这里需要区分侧向和横摆的定义:
侧向:车辆沿y轴方向的运动。
横摆:车辆绕z轴的转动。
4.1.1侧向运动
①(本文仿真选用)
符号说明:m、ms分别为半车质量和簧载质量,vy为侧向速度,θ为侧倾角,ψ为横摆角位移,vx为纵向车速,Ff、Fr分别为前后轮胎侧偏力,所有接下来还要提到轮胎模型。本来想着左右侧倾悬架匹配左右轮胎模型,但是发现转向模型一般为线性二自由度理论模型是前后轮的,看了好几篇文献都是这样假设的,那我也这样理想假设考虑吧。
注:前面说过,侧倾角本身就很小,而沿着侧向运动的分量就更小,所以有的文献在建模时会忽略这一部分侧向位移,即ms*h*θ'',则侧向运动方程为:
②
4.1.2横摆运动
![]()
符号说明:a、b分别为前后轮到质心的距离,Iz为绕z轴的转动惯量即横摆转动惯量。
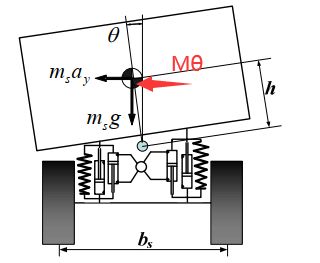
4.1.3 因转向带来的侧倾力矩
实际上,由于转向操作的侧向和横摆运动会带来侧倾力矩,建模中这部分是不可忽略的。
所以上述的半车侧倾运动要加上转向操作带来的侧倾力矩,即:
4.2 轮胎模型
由于实际过程中的耦合关系,所以需要提出轮胎模型进行反映,即得到轮胎侧向力和回正力矩。而轮胎模型以郭孔辉院士提出的UniTire 和 Pacejka 提出的 Magic Formula 为代表。
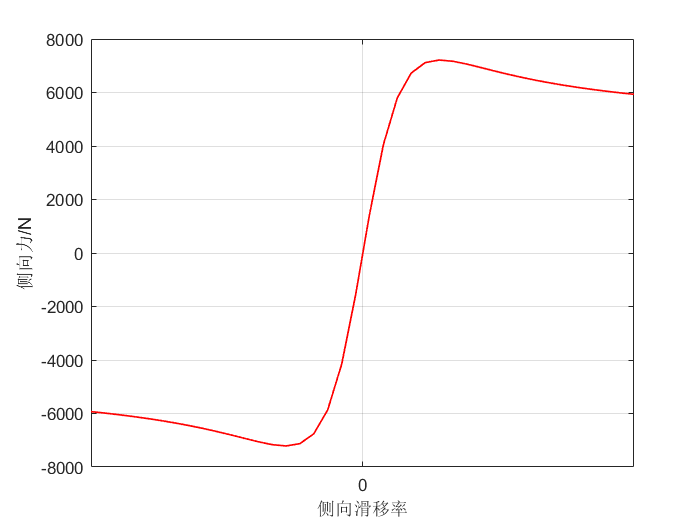
轮胎侧向力与滑移率的关系曲线为:
而有的文章也会对其简化,仅为了得到轮胎侧向力即可,假设在小转角条件下,轮胎特性可认为是线性的,则轮胎侧偏力(本文仿真选用)为:
若考虑侧倾影响,则轮胎侧偏力为:
符号说明:kf、kr分别为前、后轮胎侧偏刚度;αf、αr分别为前、后轮胎侧偏角;Ef、Er分别为前、后侧倾转向系数;δ为前轮转角。
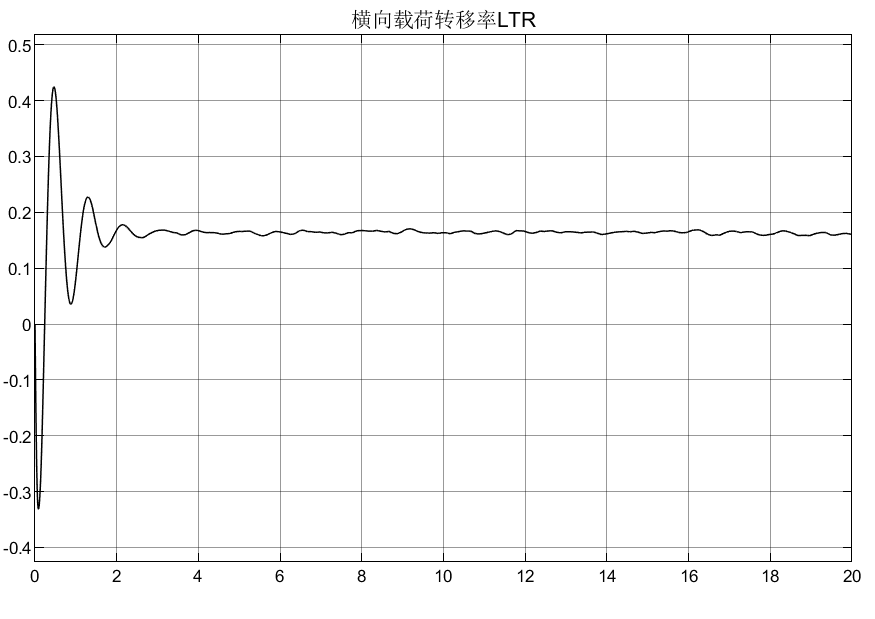
4.3 横向载荷转移率
横向载荷转移率 (LTR)是常用的预测车辆抗侧翻指标,可表示为:
符号说明:Ix为车身ms绕x轴的转动惯量,即簧载质量侧倾转动惯量;d = bs/2即轮距(假定前后轮距相等)。
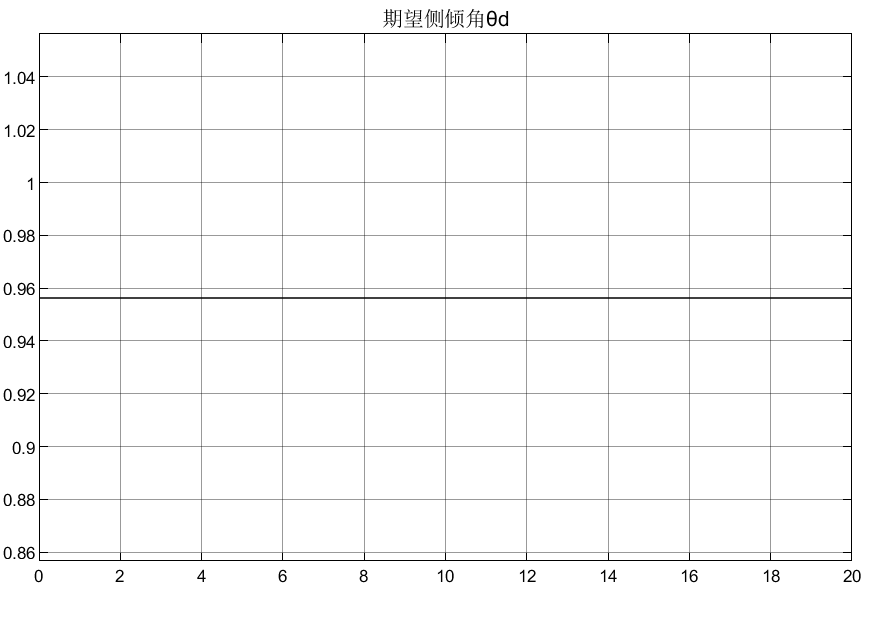
4.4确定期望的侧倾角
转向时产生的侧倾力矩为:
重力产生的侧倾力矩为:
![]()
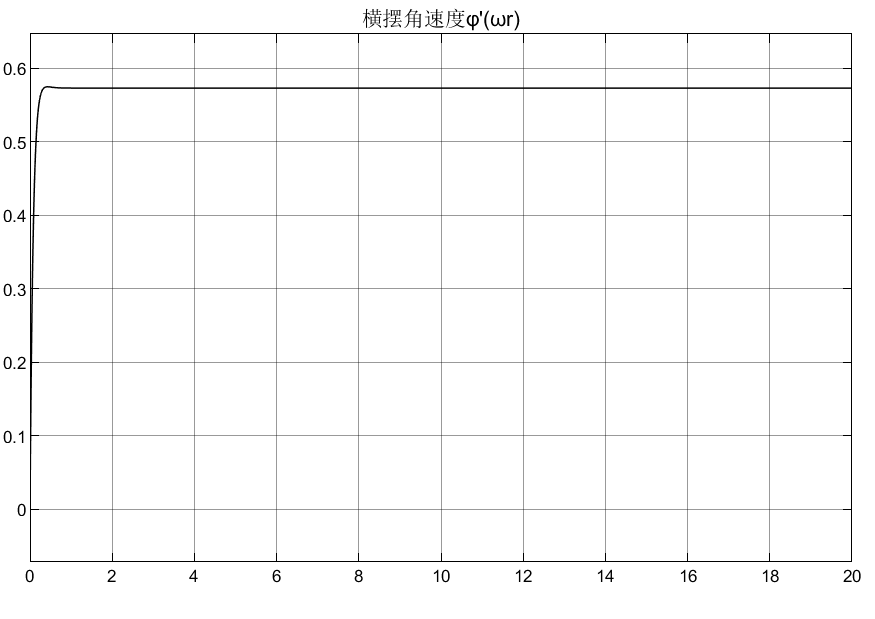
理想时,希望转向操纵带来的侧向加速度为0,即ay = 0;并且希望此时是理想的中性转向,所以此时的横摆角速度为:
4.5 simulink仿真分析
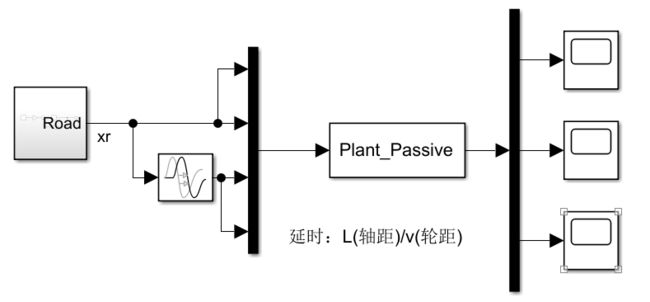
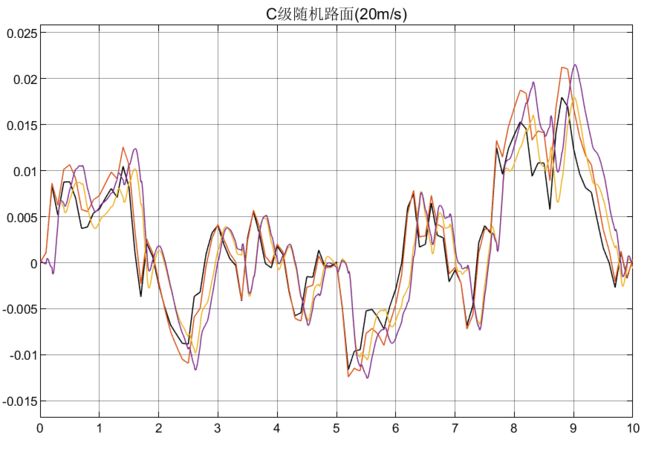
4.5.1 考虑相干性、延迟性的整车随机路面激励
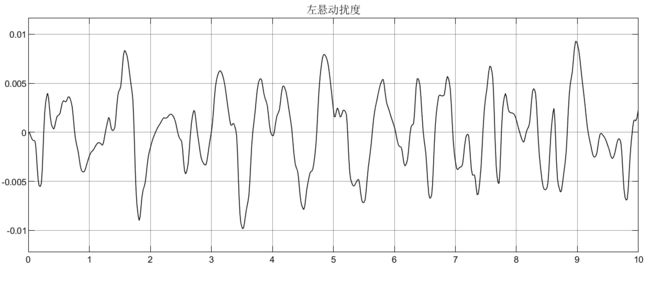
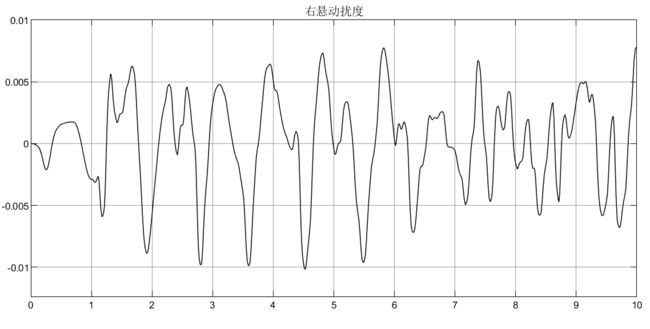
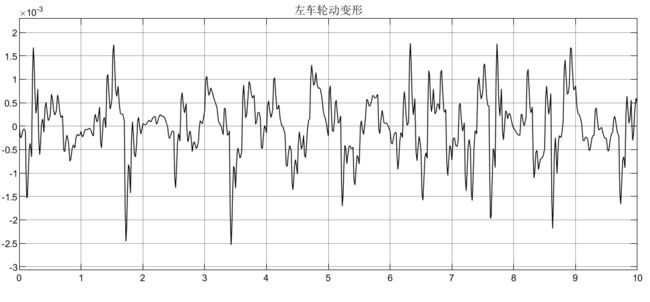
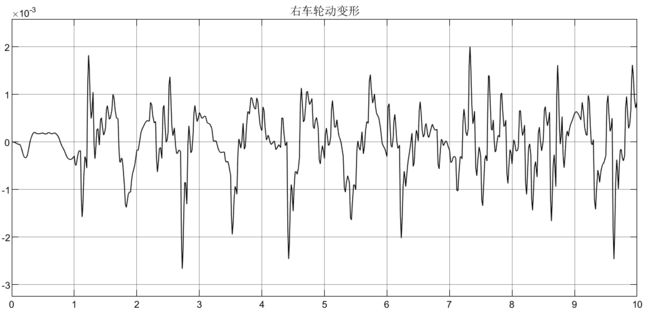
为了更加严谨考虑,这里采用C级随机路面激励,并且左右轮考虑相干性,前后轮考虑延迟性:
① 考虑左右轮的相干性,前半车左右轮C级随机路面激励:
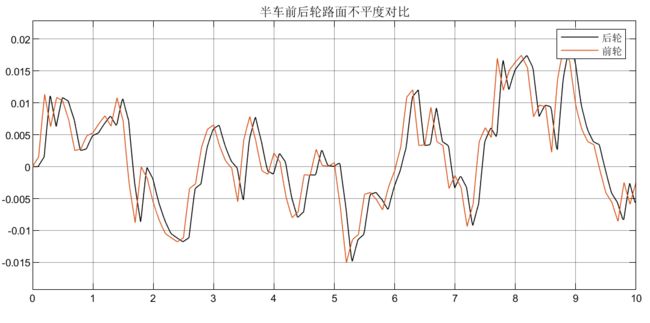
② 考虑前后轮的延时性,半车前后轮C级随机路面激励:
4.5.2 2自由度转向+4自由度半车侧倾模型
注意这里方程转向4阶+侧倾8阶,但是侧倾角速度2阶重复定义了,所以总阶数=4+8-2=10,所以定义10个状态变量:
![]()
这里先以被动悬架为例,在前轮转角5°和C级随机路面的扰动输入下,仿真如下:
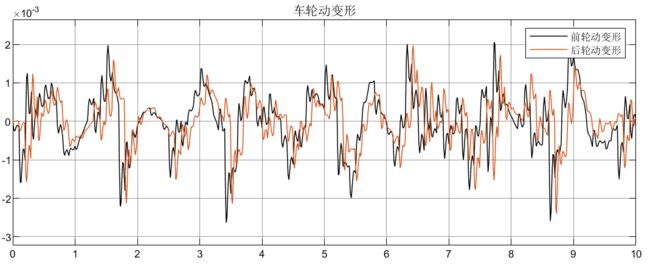
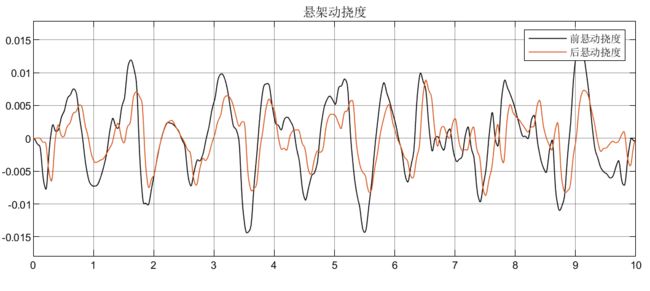
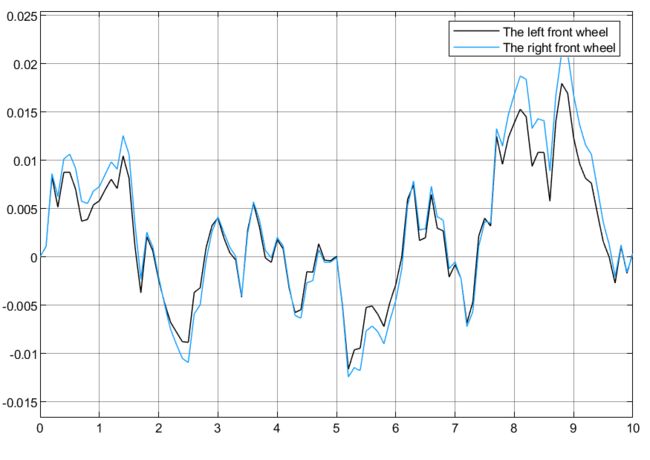
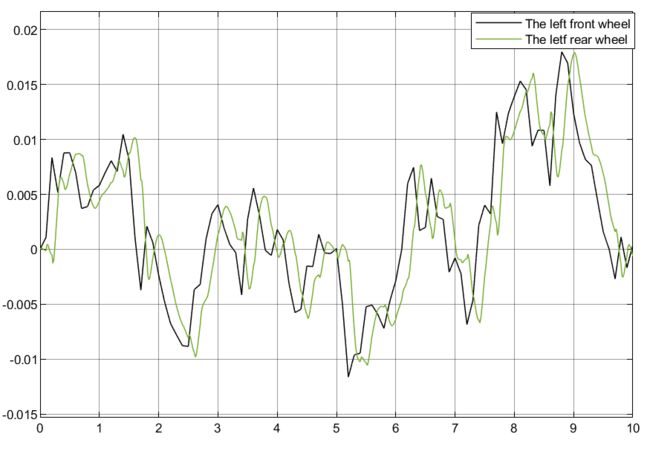
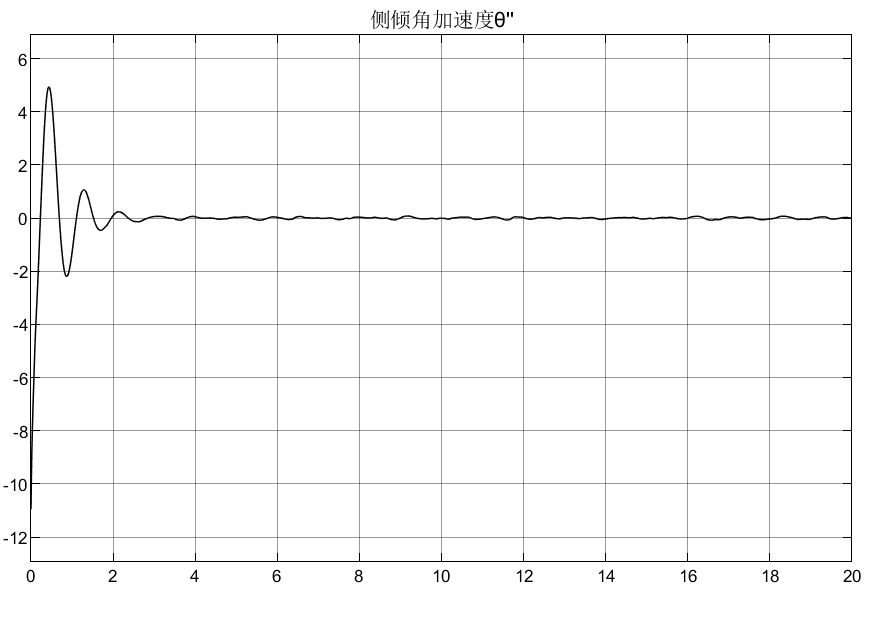
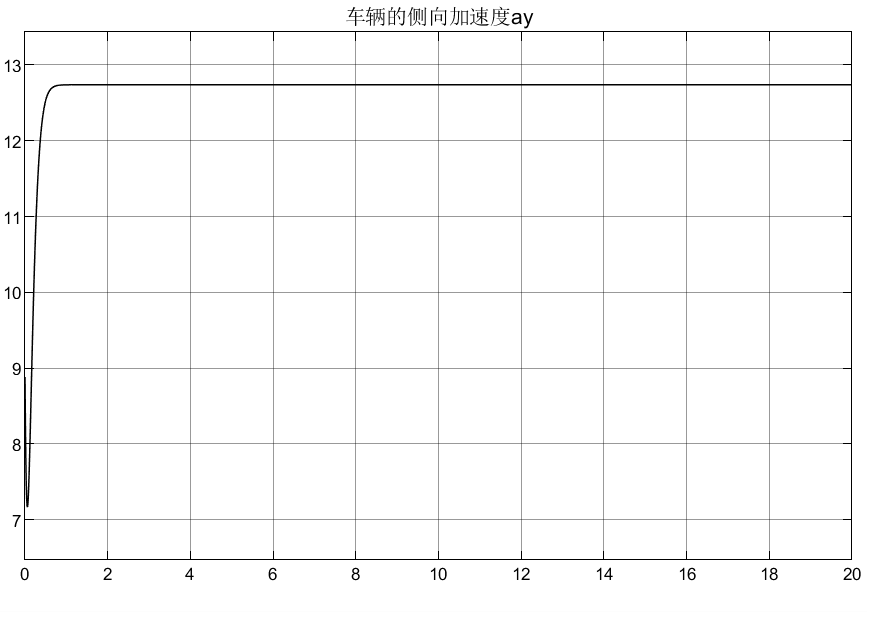
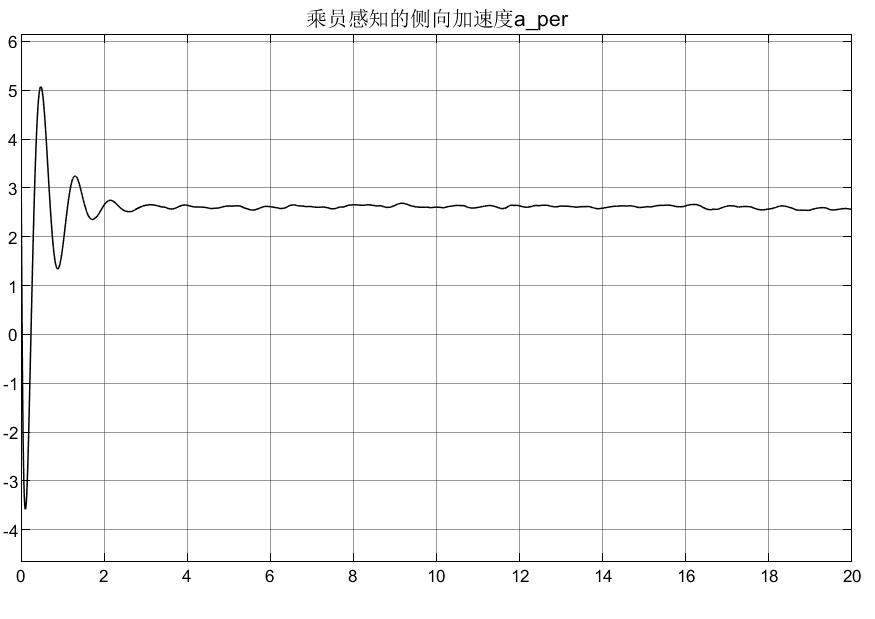
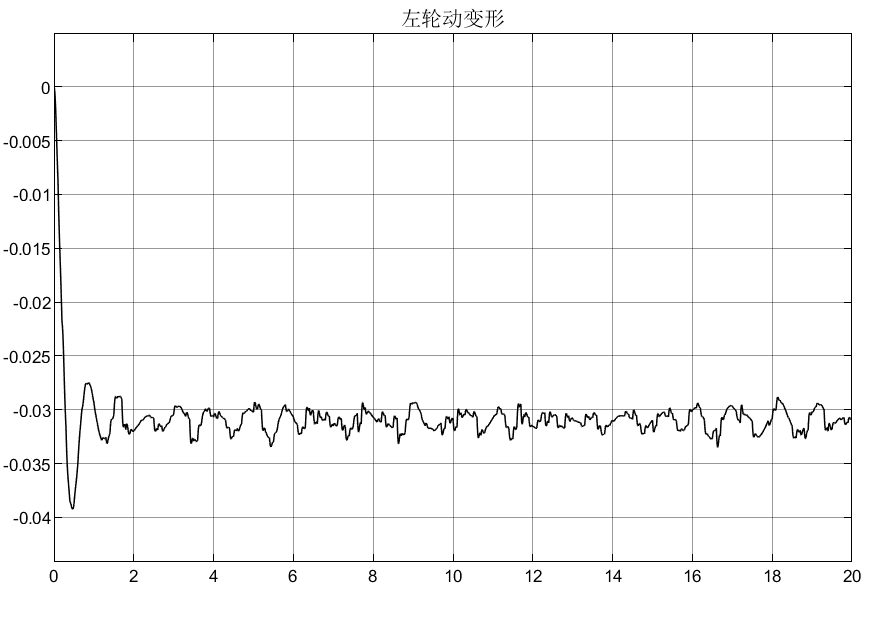
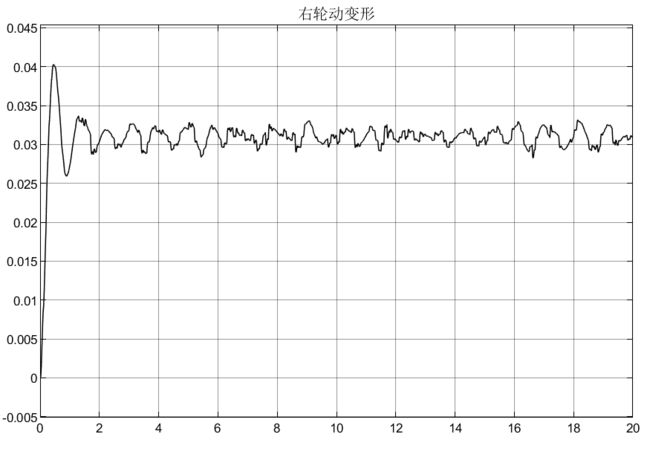
4.5.3 2自由度转向+4自由度半车侧倾模型(被动)仿真结果
可以看到,被动悬架表现的效果很差;从车轮动变形和悬架动扰度可以看出是对称的效果,说明符合实际的转向,同时也解释了车辆在过弯道时为什么能够主动向内侧倾斜。
4.5.3滑模控制器设计
①设计滑模面
![]()
求导之后:
其中:
![]()
注:对于滑模面为什么这样选取?因为控制目标是防侧倾,所以取实际侧倾量和理想侧倾目标的误差为变量,并含其导数、本身和积分3项。
②选取指数趋近律:
![]()
联立:
所以控制律为:
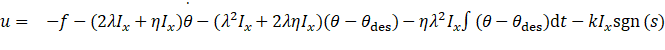
注: η为指数项增益决定收敛速度,理论上要大;k为切换增益决定趋近速度,越大趋近速度越快但抖阵越大,为保证快速趋近同时减小抖振,所以要将η调节大些,k调节小些(但是要>扰动+不确定量)。
4.5.4 转向+半车侧倾悬架滑模控制仿真
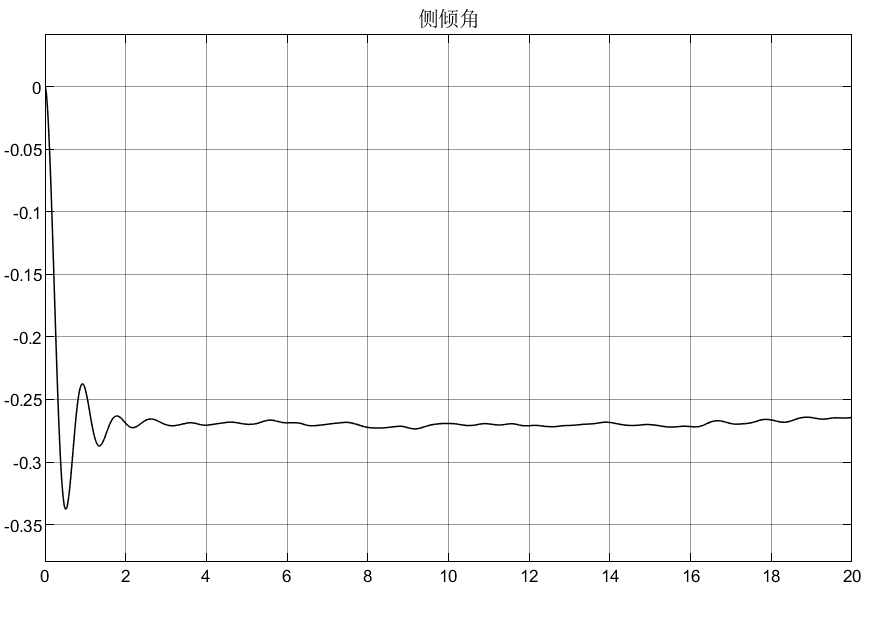
4.5.5 2自由度转向+4自由度半车侧倾滑模控制主动悬架仿真结果
这篇滑模控制文献数值和参数有好多问题,其滑模控制原理不难,额,现在没那么多时间去调试,后面闲的时候再补吧,抱歉了!
未完待续.......
左侧的悬架控制力与右侧的悬架控制力在方向上相反,这也就解释了车辆在过弯道时为什么能够主动向内侧倾斜。
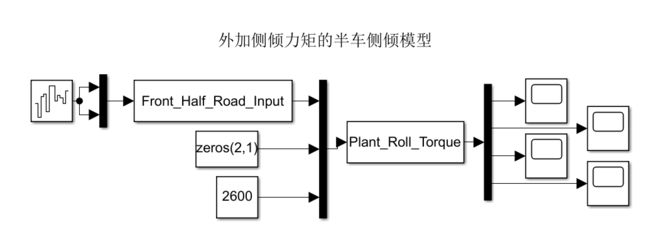
5.侧倾力矩+侧倾4自由度模型(不建议)
如果不精确要求考虑转向模型导致的侧倾运动,则在侧倾模型之上直接加上一个侧倾力矩即可,因为理想情况下,车辆的重力力矩完全可以补偿因转向而产生的离心侧倾力矩,这样侧倾运动为:
即第2节中的侧倾模型变为:
5.1 仿真分析
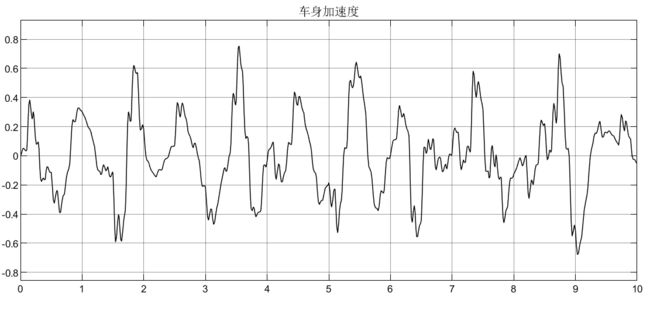
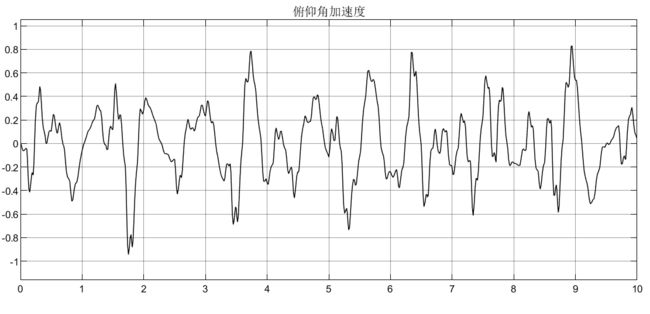
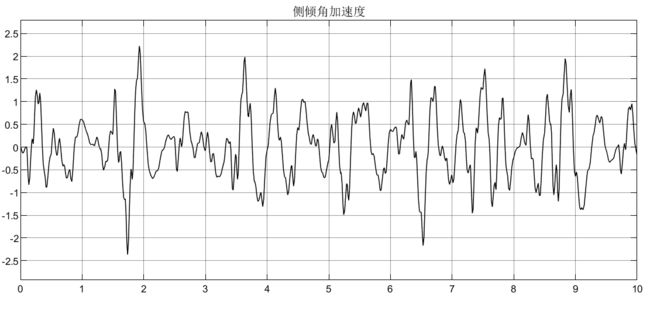
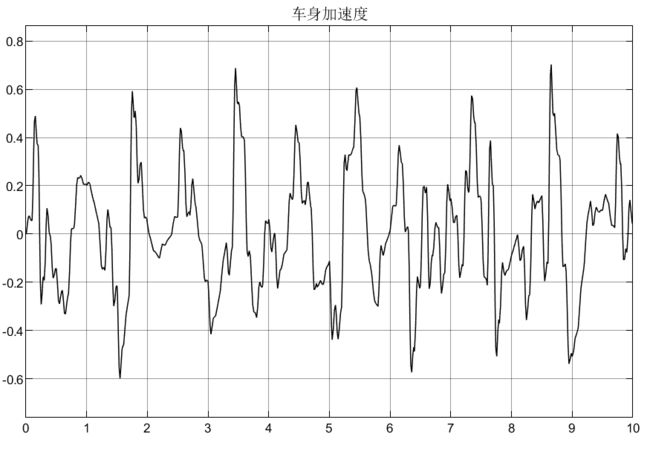
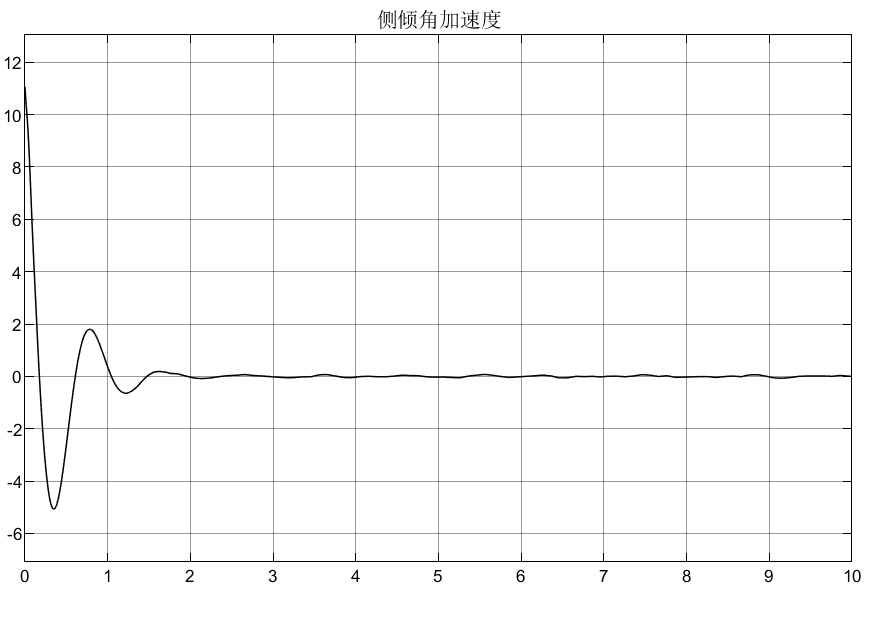
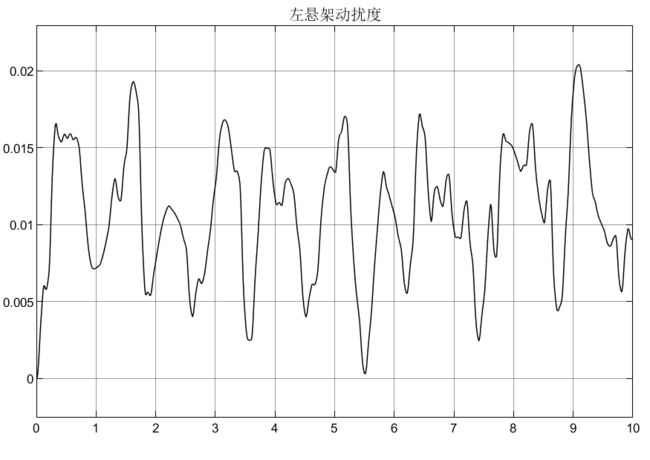
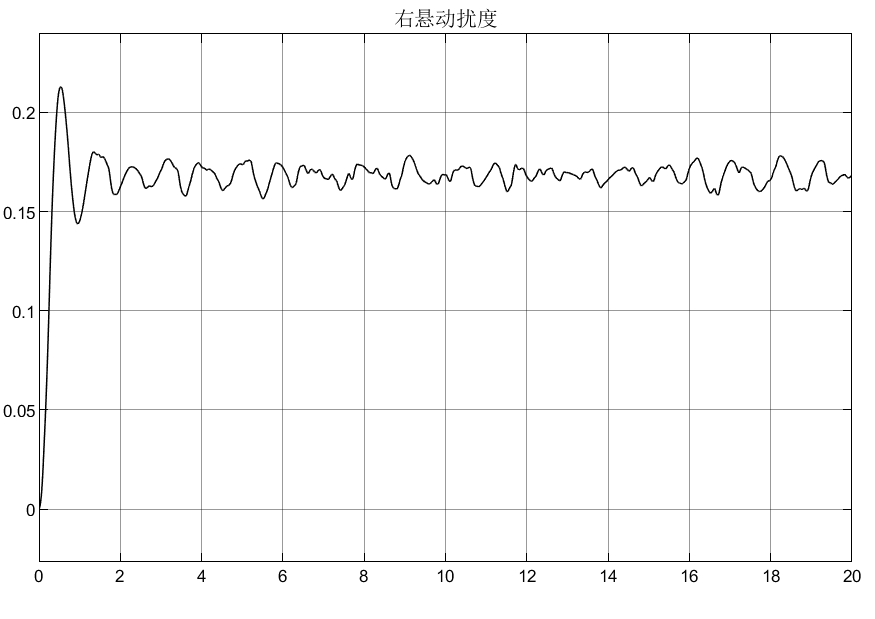
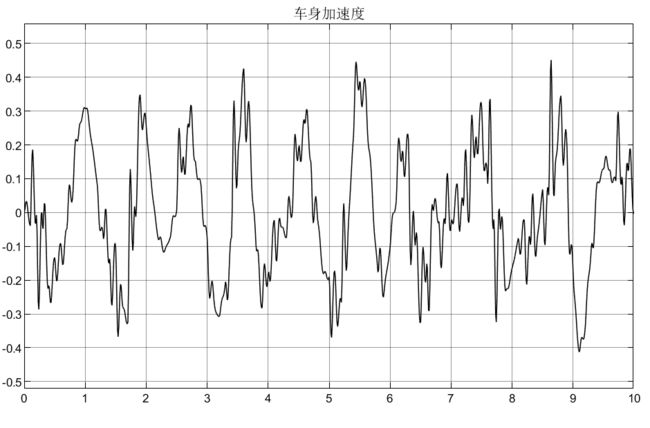
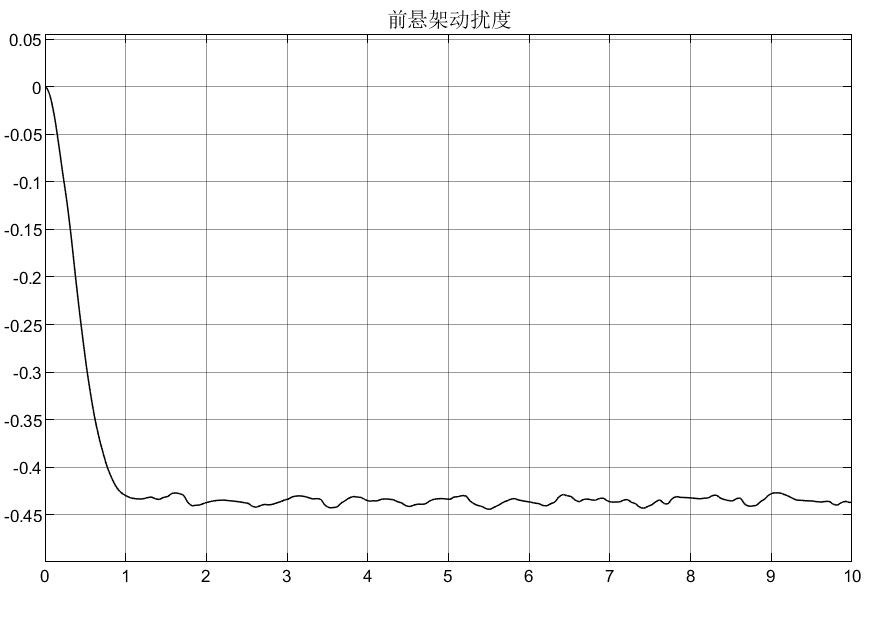
比如Mθ = 2600N/m,仍以被动悬架为例,仿真如下:
![]()
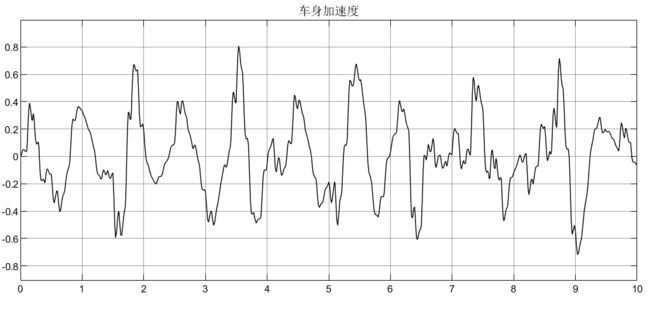
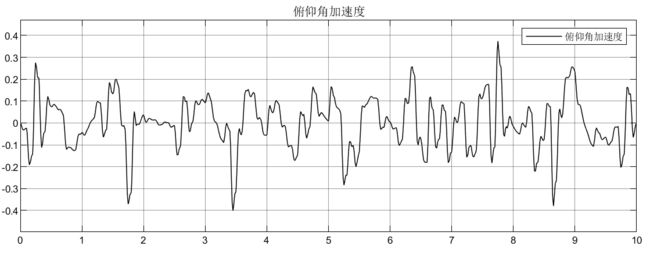
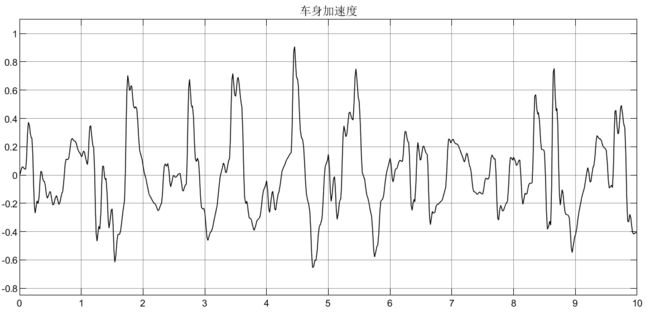
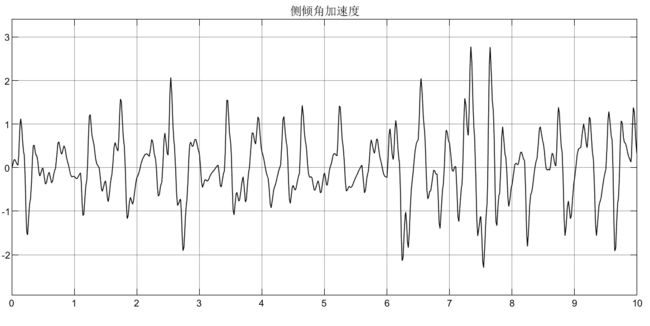
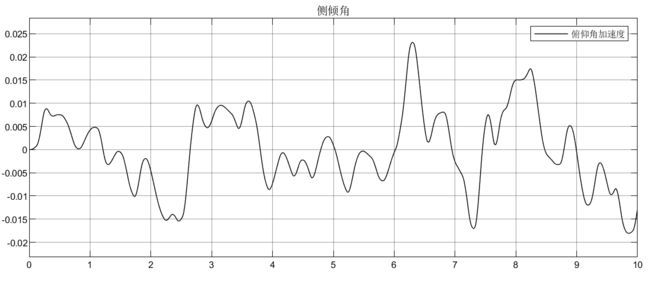
可以看到,车身加速度由于不含侧倾力矩,所以没有受到影响,侧倾加速度在2600N/m的力矩下,初始产生较大的侧倾加速度,这显然在实际过程中是不允许的,所以要添加控制器;悬架动扰度和车轮动变形均受到侧倾力矩的影响;从侧倾力矩的表达式可知它的产生是由多个因素引起的(如转向、坑洼路面等),所以在模型设计时可以结果实际需要去添加。
6.转向 +半车俯仰悬架(6自由度)模型
6.1仿真结果
未完待续.....
7.转向 +整车悬架(9自由度)模型
7.1模型自由度计算
转向2自由度 = 1个自由度的侧向运动+1个自由度的横摆运动,俯仰运动1一个自由度,侧倾运动1一个自由度,车身垂向运动1个自由度,4个车轮的垂向运动4个自由度,2+1+1+1+4 = 9。所以转向+整车模型是9自由度.
7.2转向工况下的整车数学模型推导
7.2.1 转向运动方程
符号说明:m和ms分别为整车质量和簧载质量,β为质心侧偏角,ωr为横摆角速度,Fy1为2个前轮的侧偏力和,Fy2为2个后轮的侧偏力和,φ为侧倾角。
7.2.2 侧倾运动方程
![]()
7.2.3 俯仰运动方程
7.2.4 车身垂向运动方程
![]()
7.2.5 车身垂向运动方程
![]()
其中,在考虑横向稳定杆的作用下,有:
符号说明:kaf和kar为横向稳定杆角刚度。
假设侧倾角和俯仰角很小,则有:
7.2.6轮胎侧偏力
假设小转角下轮胎是线性的,且考虑侧倾的影响,则有:
7.3 状态变量和输入选取
7.3.1状态变量
![]()
7.3.2扰动输入
![]()
7.3.3控制输入
![]()
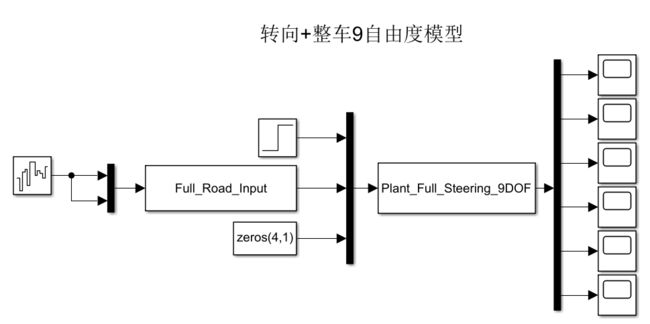
7.4Simulink模型
以被动悬架在角阶跃输入5°下(注:这里要注意matlab给的前轮转角数值输入是弧度,所以变成角度时要*Π/180才是角度输入)的仿真为例,并选取如下参数:
m = 1551.8;ms = 1380;Ix = 235;Iy = 1222;Iz = 850;
mu1 = 40.5;mu2 = mu1;mu3 = 45.4;mu4 = mu3;
ks1 = 17000;ks2 = ks1;ks3 = 22000;ks4 = ks1;
kt1 = 192000;kt2 = kt1;kt3 = 192000;kt4 = kt3;
a = 1.07;b = 0.76;d = 0.65;
Ef = -0.115;Er = 0;%前侧倾、后侧倾转向系数
h = 0.505;u0 = 20;
g = 9.81;c1 = 1500;c2 = c1;c3 = 1500;c4 = c3;%悬架阻尼系数注:模型参数的选取和仿真结果有较大的差异,甚至可能导致仿真结果错误,以上参数来自《车辆悬架系统振动控制---张进秋等》 。
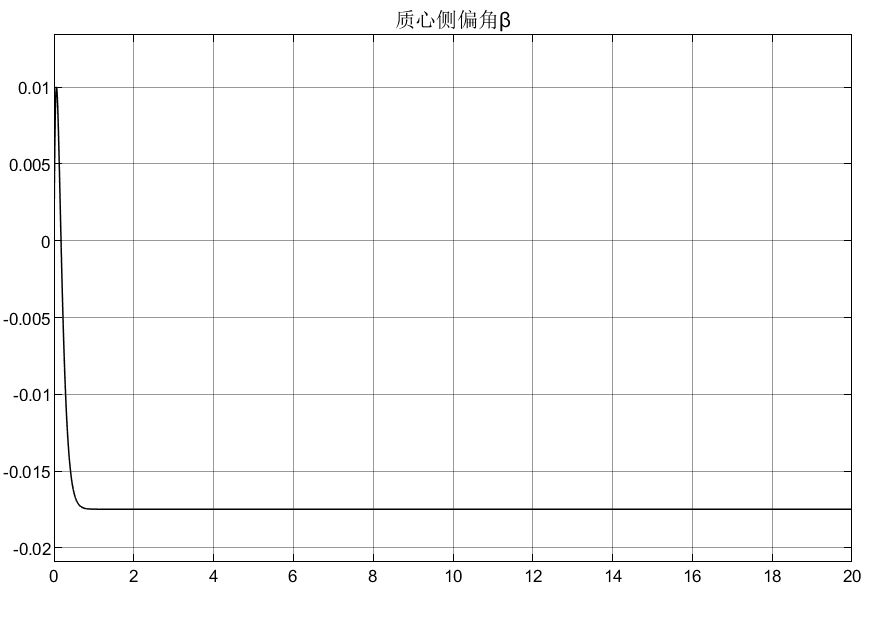
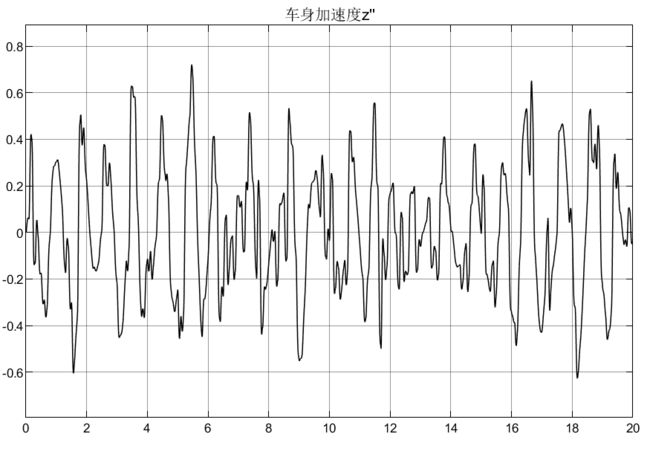
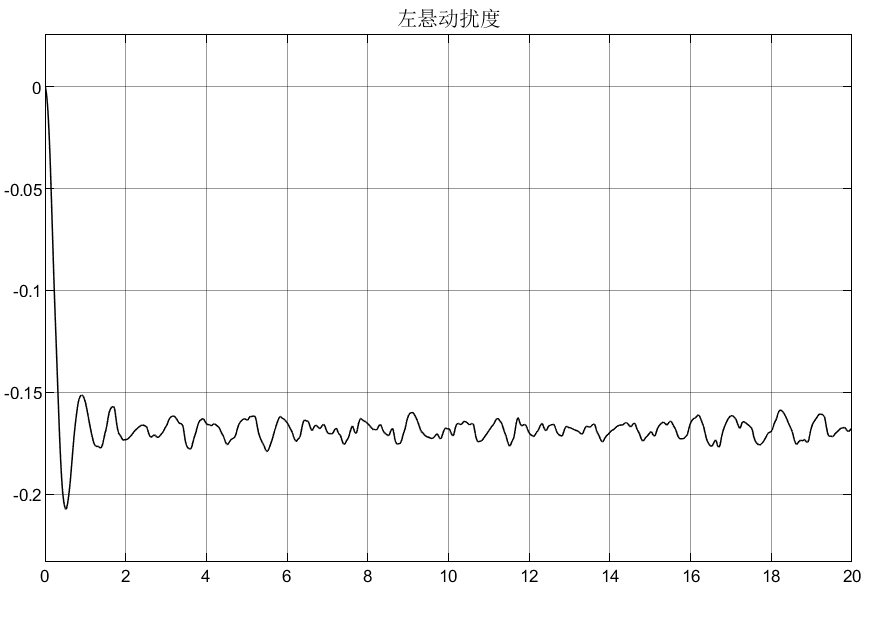
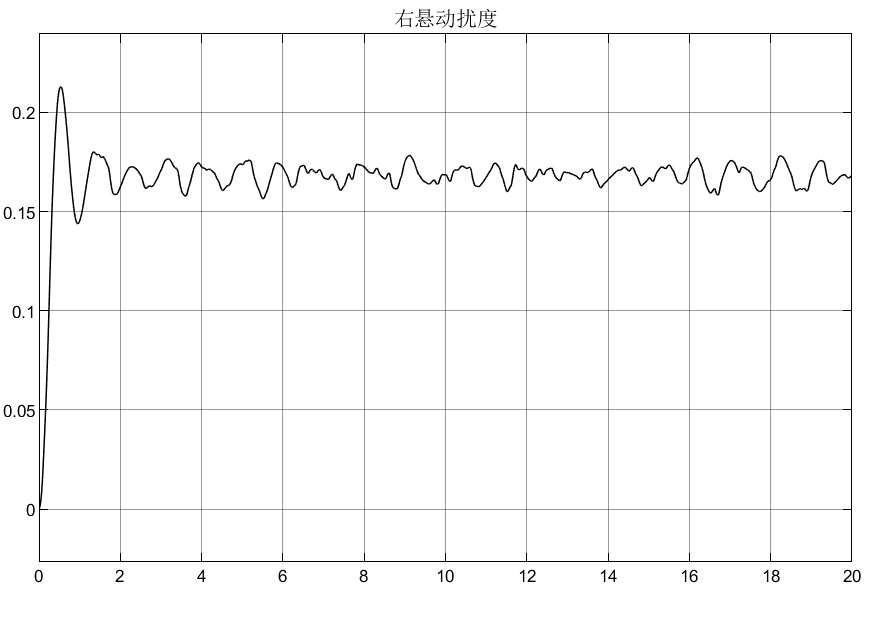
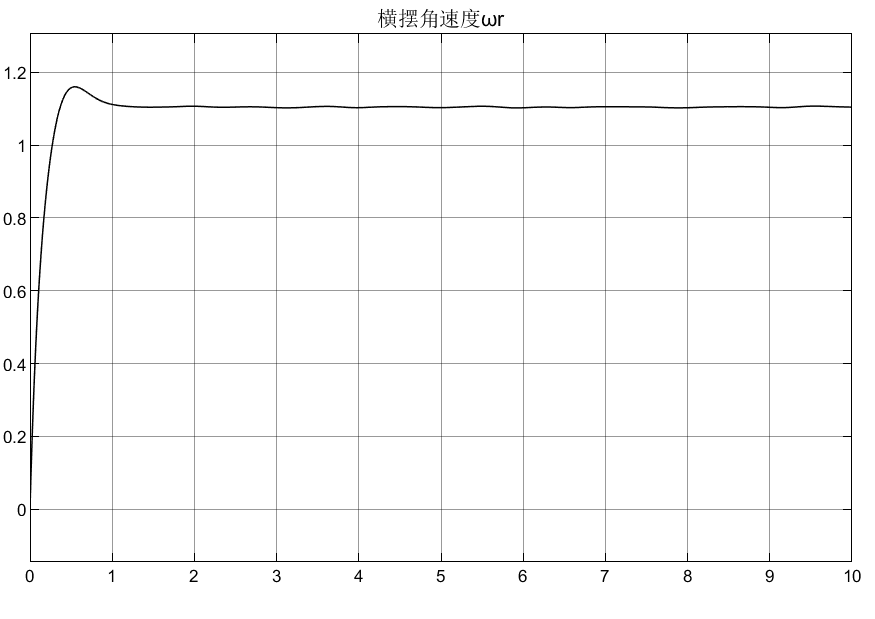
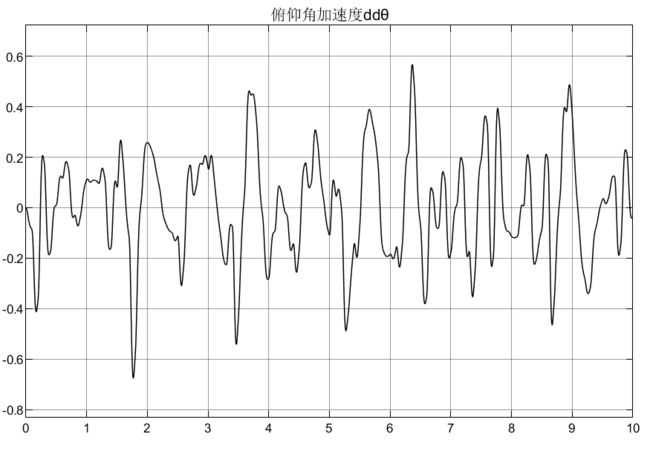
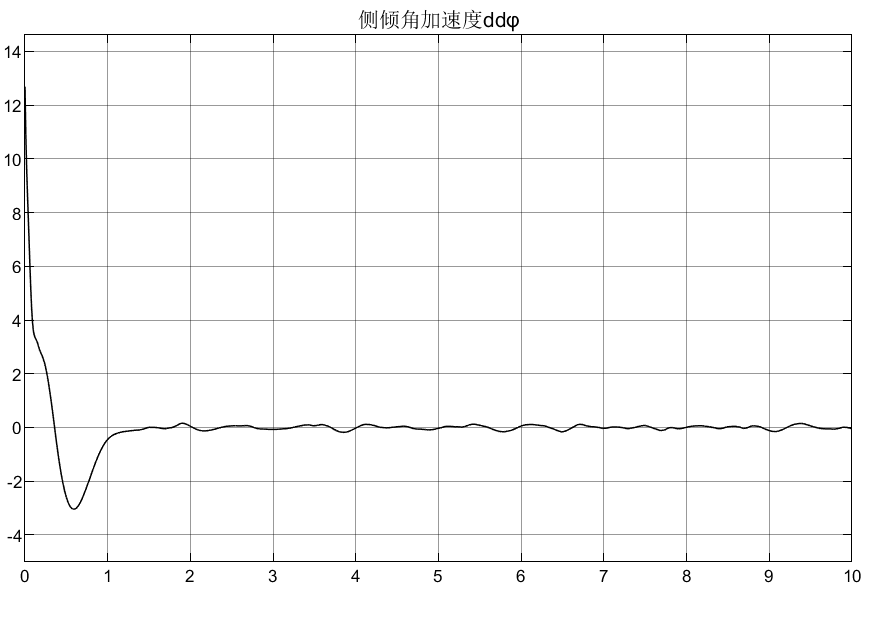
7.5 仿真结果
![]()
如果有帮助,麻烦帮忙点个赞是我最大的分享动力,非常感谢!
注:仅为便利自己学习,错误在所难免,如有侵权,请联系删除,有兴趣的学者可以参考学习交流,谢谢!
参考资料:
《基于主动悬架的车辆主动侧倾控制研究---姚嘉凌等》
《阻尼连续可调的汽车磁流变半主动悬架控制方法研究》
《S双模式互联悬架与主动前轮转向集成控制研究》
《基于主动悬架的车辆主动侧倾滑模控制研究---任杉》
《转向工况下车辆主动悬架的侧倾控制---陈建国》
《抑制侧倾的主动悬架控制方法研究---嵇俊达》
《整车主动悬架系统的数学建模---张衍成等》
《车辆悬架系统振动控制---张进秋等》