深度学习分享1：神经网络概念

先给自己挖个坑哈哈

大家好，第一次在全国大型同性交友平台csdn上写博客，想想还有点小激动呢。本人学渣一枚，写这些笔记纯属整理思路，有错误开黄腔大家多多指教哈。希望可以通过这种方式交到一些志同道合的朋友，有道是玩的好不如排的好，队友给力自己哪怕是混子段位也上去了。

准备工作

python基本语法，高数（多元函数微分学），线代（矩阵运算，点积），概率论（高斯分布要知道吧），数值分析（知道什么是迭代就可以了）真的不是要把这些学得很精通，需要用到什么再去学，要有针对性，有了这些就可以开始学习bp神经网络了，bp神经网络是基础，很重要

基础性概念简介

这些内容需要慢慢熟悉，多接触就不会忘了，我简单梳理一下

大学生都知道的概念

测试集，训练集，样本，特征，标记，矩阵，点积，乘积，向量，线性，非线性，偏置，转置，二分类，阈值，略，自行百度

张量

可以理解为多维矩阵

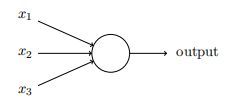
感知器

x1，x2…是输入，它们分别乘以w1，w2…,然后求和，得到一个输出，可以设置阈值，比如输出大于阈值为1，小于阈值为0等，实现了二分类。
在深度学习中一般把这些w_i和x_i合起来写成张量形式，可能是很多维的，那么output=w.x。
向量是行向量列向量自己规定，必要时可以转置 。

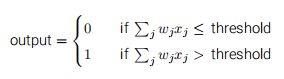
可以在计算中加入偏置b，这样就代替了阈值，那么就变成了

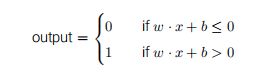
感知器可以模拟与非门，学过数字电路的同学应该深有体会，但是除此之外好像没什么特别的，也不能解决非线性问题，但是复杂的模型就是由这些简单的模型不断优化得来的。

s型神经元

我们把感知器拓展到三层，第一层就叫输入神经元，第二层叫隐藏层（隐藏层可以有很多层），第三层叫输出神经元，这样的话w会有很多的脚标，每一条连线对应一个w，现在暂时不谈标记的规则，总之就是很多很多的w，w被叫做权重。想想如果把训练集的特征（x₁，x₂…）分别乘以权重（w₁，w₂…），一层层下去得到一个输出，这个过程叫前向传播。这个输出与标记相比有误差，那说明我们这个模型不够准确，这个误差就叫做损失函数（损失函数有很多种，需要考虑实际情况），我们需要反过来调整w使得误差越来越小，这个过程叫反向传播，而反向传播需要使用一种算法叫梯度下降法(先挖一个坑)，一次性搞不定，需要很多次反向，这个次数叫纪元，我们想要一个非线性模型，要把每一层的输出做非线性变换，比如把输出加一个ln等，这个过程叫逻辑回归

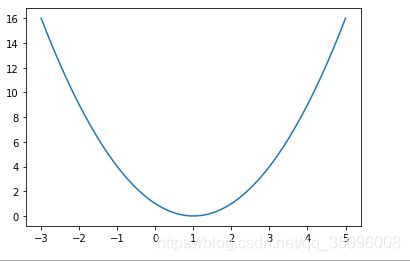
梯度下降法简介

import matplotlib.pyplot as plt
import numpy as np
x =np.linspace(-3,5,50)
y=(x-1)**2
plt.figure()
plt.plot(x,y)
plt.show()

import tensorflow as tf
w=tf.Variable(tf.constant(5,dtype=tf.float32))#设定一个常量为5，类型是float32，并将其设置为变量，这一步是初始化的作用
lr=0.01
epochs=40
for epoch in range(epochs):
    with tf.GradientTape() as tape:
        loss=tf.square(w-1)
    gradient=tape.gradient(loss,w)
    w.assign_sub(lr*gradient)
    print('After %s epoch，w is %f,loss is %f'%(epoch,w.numpy(),loss))

bp神经网络

上面讲的一大堆东西和过程再加上之后要讲的优化算法等等合起来叫bp神经网络

装b英文

熟悉这些概念的英文很重要，装b必用
权重weights
梯度下降法 gradient descent
代价（损失）函数 (overall) cost function
前向输送 Feedforward
反向传播 Backpropagation
神经网络Neural network
方差 squared-error
均方差 average sum-of-squares error
偏置项 bias terms
激活函数 activation function
学习速率 learning rate
线性叠加 linear superposition
纪元epoch
逻辑回归logistics regression

举一个屌丝都喜欢的例子

现在你想找一个女朋友，假设你依照的是bp神经网络的模型（其实很贴切），你有很多个yy的对象，这些对象对应训练样本，用于训练模型。在训练样本中随便找一个女生，她有很多特点，比如肤白貌美程度，年龄，身材，学历，性格，家庭条件，情商，智商，兴趣，契合度等等，这些对应特征。你心中对每个样本都有一个整体印象打分，这些打分都是准确的，这对应标记。现在的情况就是你对她们有一个整体的认识（打分），但是你对她们具体的特征占了多少权重是模糊的，连你也说不清楚自己喜欢什么样的。
开始训练，把一个样本的这些特征排列成向量输入这个模型，一个特征对应一个输入神经元，那么输入层就搞定了。我们待会说有隐藏层的情况，先说输入层直接到输出层，输出层只有一个神经元，把输入层与输出层连接起来，每个连线都有一个权重，比如你自己觉得肤白貌美对你最重要，权重设为0.5，年龄不是问题，权重设为0，身材设为0.3，学历设为-0.1，性格也很重要，设为0.49999999，家庭条件不太重要，设为0.05，这些叫初始权重，就是你也不确定的权重…最后加权求和得到一个输出，这个过程叫前向传播，你想把事情搞得复杂一点，把输出加一个非线性函数，这个过程叫逻辑回归，如果你发现输出与你打的分不同，这里有一个损失函数，说明有误差，这些权重不是你真正的想法，需要调整，于是开始用损失函数对权重求偏导数，反向传播，运用梯度下降法更新权重，使得损失函数达到极小值，这样你就求出了所有的权重，等到下次你遇到一个新的女生，你把特征带入这个模型，就可以得到她的分数了。
那如果有隐藏层是什么情况呢？这其实就是一种组合，比如肤白貌美和身材的组合，继续传播权重陡然增大，就产生了1+1>2的效果，总之每个特征的评价都不是简简单单的，它们之间存在着交相辉映或者负负得正的复杂关系，先告诉大家一个证明，三层神经元可以解决多个对象的问题，逻辑回归可以模拟所有的非线性问题，至于怎么用数学来严格证明，这是一个巨大的坑。
强调一下，这个例子中的已知是特征和整体印象，未知量是权重，整个过程是在求权重的张量，就好比你嘴上说着非富不嫁，你以为这一项的权重很高，最后你可能嫁给一个流浪诗人，因为可能文艺占了更高的权重，而富有的权重没你想的那么高，你通过大量的样本就可以搞清楚自己真正喜欢的是什么，这像是一个试错然后修正的过程，神经网络真的跟我们大脑的机理很相似，虽然现在大脑的真正原理并未被知晓。

直接从toy project手写数字识别开始

为什么我不先说说什么是机器学习，什么是深度学习呢？个人认为学习最好的方法其实是做一件事情，有一个目标，然后完成这件事需要用到什么，你学完一大推理论干不成事总是会有些沮丧可能也学得不牢靠，相反你做成一件事学会了一堆理论就会很有成就感，当然这种事情仁者见仁智者见智。手写数字识别算是入门级别的toy project了吧，虽然是入门，但是深入挖掘可以搞懂很多东西，是为进阶做准备的好项目

神经元模型可以模拟任意函数的数学基础

从这里可以看出，一个复杂的多元函数都可以近似表示成关于这些自变量的一阶泰勒展开，因此，这个模型可以模拟许许多多的函数，也就可以解决很多现实问题。