机器学习-白板推导-系列(十)笔记:EM算法
文章目录
- 0 笔记说明
- 1 算法收敛性证明
- 2 公式导出
-
- 2.1 ELBO+KL Divergence
- 2.2 ELBO+Jensen Inequlity
- 2.3 最后的工作
- 3 从狭义EM到广义EM
- 4 广义EM
- 5 总结
0 笔记说明
来源于【机器学习】【白板推导系列】【合集 1~23】,我在学习时会跟着up主一起在纸上推导,博客内容为对笔记的二次书面整理,根据自身学习需要,我可能会增加必要内容。
注意:本笔记主要是为了方便自己日后复习学习,而且确实是本人亲手一个字一个公式手打,如果遇到复杂公式,由于未学习LaTeX,我会上传手写图片代替(手机相机可能会拍的不太清楚,但是我会尽可能使内容完整可见),因此我将博客标记为【原创】,若您觉得不妥可以私信我,我会根据您的回复判断是否将博客设置为仅自己可见或其他,谢谢!
本博客为(系列十)的笔记,对应的视频是:【(系列十) EM算法1-算法收敛性证明】、【(系列十) EM算法2-公式导出之ELBO+KL Divergence】、【(系列十) EM算法3-公式导出之ELBO+Jensen Inequlity】、【(系列十) EM算法4-再回首】、【(系列十) EM算法5-广义EM】、【(系列十) EM算法6-EM的变种】。
下面开始即为正文。
1 算法收敛性证明
最大期望算法(Expectation-Maximization algorithm,EM算法)是一类通过迭代进行极大似然估计的优化算法,通常作为牛顿迭代法的替代,用于对包含隐变量(latent variable)或缺失数据(incomplete-data)的概率模型进行参数估计。
迭代公式如下:

其中x为数据,z为隐变量,θ(t)为t时刻的参数,θ(t+1)为t+1时刻的参数,log p(x,z|θ)称为对数联合概率,p(z|x,θ(t))为后验概率。下面证明p(x|θ(i))是单调递增的,其中i=1,2,…,t,t+1,…证明过程如下:

即对Δ式左右两边积分后:【左边=log p(x|θ)=右边=Q(θ,θ(t))-H(θ,θ(t))】。而:

又:

现在引入KL散度:KL散度(Kullback-Leibler divergence),亦称相对熵(relative entropy)或信息散度(information divergence),可用于度量两个概率分布之间的差异。给定两个概率分布P和Q,二者之间的KL散度定义为:
![]()
其中p(x)和q(x)分别为P和Q的概率密度函数。这里假设两个分布均为连续型概率分布;对于离散型概率分布,只需将定义中的积分替换为对所有离散值遍历求和即可。KL散度满足非负性,即KL(P||Q)≥0,显然:

所以:

对于【左边=log p(x|θ)=右边=Q(θ,θ(t))-H(θ,θ(t))】,有:

又因为:

且:

所以Δ1≥0,且Δ2≥0,故:Δ1+Δ2≥0,所以:

上式≥0,因此:
![]()
由此:p(x|θ(i))是单调递增的,其中i=1,2,…,t,t+1,…。而p(x|θ(i))是概率,一定有p(x|θ(i))∈[0,1]。如果递增序列{an}有上界,则它是收敛的。因此p(x|θ(i))是收敛的。
综上所述,EM算法具有收敛性。
2 公式导出
第二节,即本节的内容是推导迭代公式是如何得出的,其中迭代公式如下:

其中x为数据,z为隐变量,θ(t)为t时刻的参数,θ(t+1)为t+1时刻的参数,log p(x,z|θ)称为对数联合概率,p(z|x,θ(t))为后验概率。
使用两种方式推导迭代公式,分别对应于2.1节与2.2节,如下。
2.1 ELBO+KL Divergence
假设z为连续型变量,设q(z)为隐变量z的概率分布,且q(z)≠0,则log p(x|θ)可写为:

上式左右两边先同乘q(z),然后都关于z求积分得:

上图将右式积分后的两项分别称为ELBO和KL Divergence,即log p(x|θ)=ELBO+KL[q(z)||p(z|x,θ)],其中ELBO即Evidence Lower Bound,翻译为证据下界,KL Divergence即KL散度,在【1 算法收敛性证明】一节提到过,再次贴出公式:
![]()
KL散度满足非负性,即KL[q(z)||p(z|x,θ)]≥0。当且仅当P=Q时,KL(P||Q)=0。对于本节的KL Divergence,当:
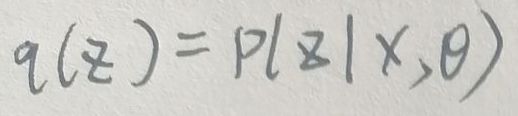
此时KL[q(z)||p(z|x,θ)]=0。一般情况下,有KL[q(z)||p(z|x,θ)]≥0,因此对于log p(x|θ)=ELBO+KL[q(z)||p(z|x,θ)],有log p(x|θ)≥ELBO,即ELBO是log p(x|θ)的下界(Evidence Lower Bound,为证据下界)。
下面使用另一种方法推导得出q(z)=p(z|x,θ)。
2.2 ELBO+Jensen Inequlity
假设z为连续型变量,设q(z)为隐变量z的概率分布,且q(z)≠0,因为:

则log p(x|θ)可写为:

下面先介绍Jensen Inequlity,即Jensen不等式。
假设f(x)是上凸函数,且其图像的一部分为:

任意取两点:(a,f(a))和(b,f(b)),已标在f(x)的图像上。c为区间[a,b]上的任意值,可设t∈[0,1],则c=t·a+(1-t)·b。根据上凸函数的性质,有:

将上面的公式进行推广,有:

上式就是Jensen不等式。下面讨论在概率中的Jensen不等式。
设X为连续型随机变量,其概率密度函数为f(x),则有:
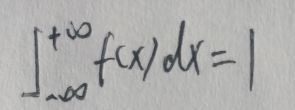
Jensen不等式变成这样的描述——如果g(x)是任意实值可测函数且φ(x)在g(x)的范围内是上凸函数,那么:
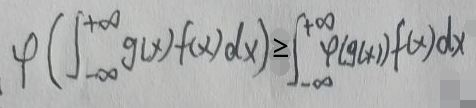
如果g(x)=x,那么Jensen不等式的形式可以简化为:

根据连续型随机变量的期望函数可得:

当且仅当x=c时等号成立,其中c为常数。现在回到log p(x|θ):

令Jensen不等式的φ(x)=log x,则φ(x)是上凸函数,可得:

其实上图右面就是ELBO。在【2.1 ELBO+KL Divergence】一节中因为KL[q(z)||p(z|x,θ)]=0时有q(z)=p(z|x,θ),下面使用另一种方法推导得出q(z)=p(z|x,θ)。
对于上面一张图片,当且仅当p(x,z|θ)/q(z)=c时,等号成立,其中c为非零常数。则:

现在同样得出了q(z)=p(z|x,θ)了!!
2.3 最后的工作
设t时刻时,有:
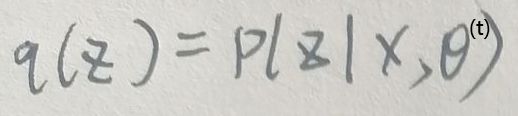
令θ(t+1)为:

而上式等于:
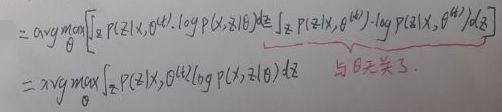
也就是:

推导迭代公式结束。
3 从狭义EM到广义EM
EM算法用于对概率生成模型的参数估计,设参数为θ,则:

由【2.1 ELBO+KL Divergence】一节可知目标函数log p(x|θ)=ELBO+KL[q(z)||p(z|x,θ)],其中ELBO是【关于参数θ和隐变量z的概率分布q(z)】的函数,为叙述方便,令ELBO=L(θ,q(z)),由KL[q(z)||p(z|x,θ)]≥0得:log p(x|θ)≥L(θ,q(z))。若q(z)=p(z|x,θ),则就是上面讨论的EM,将其称为狭义的EM。
若p(z|x,θ)无法求出,则意味着无法找到p(z|x,θ),从而无法使q(z)=p(z|x,θ)。
下面使用坐标上升法进行下一步工作。
首先坐标上升法(Coordinate Ascent)是每次通过更新函数中的一维,通过多次的迭代以达到优化函数的目的。
对于KL[q(z)||p(z|x,θ)],当q(z)→p(z|x,θ)时,即q(z)越接近于p(z|x,θ)时,KL[q(z)||p(z|x,θ)]越小。当θ固定为某一常数时log p(x|θ)就固定为一常数值,而log p(x|θ)=L(θ,q(z))+KL[q(z)||p(z|x,θ)],则求L(θ,q(z))的最大值问题就等价于求KL[q(z)||p(z|x,θ)]的最小值问题。
现在使用坐标上升法:
(1)先固定θ为一个常数,然后令q(z)的估计值为:

得到q(z)的估计值后到(2)。
(2)令q(z)=q(z)的估计值后,代入下面的公式求出θ的估计值为:

得到θ的估计值后,令θ=θ的估计值,到(1)。
这样不断循环,最后便可以得到合适的θ与q(z),使得L(θ,q(z))得到最大。
现在引出广义EM算法。
4 广义EM
广义EM算法分为两步:
1、E-step:(q(z))(t+1)为:
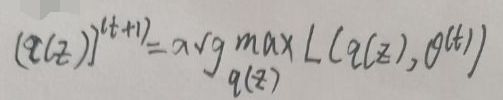
2、M-step:θ(t+1)为:

广义EM算法也是使用了坐标上升法,不断循环:先固定θ(t),然后代入第1步,求得(q(z))(t+1),然后将(q(z))(t+1)代入第2步,求得θ(t+1),将θ(t+1)作为θ(t)。
之前也提到ELBO=L(θ,q(z)),而根据【2.1 ELBO+KL Divergence】一节的第二张图片,ELBO即L(θ,q(z))为:

则:

注意公式的右面为:

于是ELBO=L(θ,q(z))=Eq(z)[log p(x|z,θ)]+H[q(z)],其中H[q(z)]是信息熵。
5 总结
狭义EM算法是广义EM算法的特例——狭义EM算法直接令q(z)=p(z|x,θ),当然这种情况下p(z|x,θ)是可求解的,这时只需要求解θ。对于广义EM算法,p(z|x,θ)是不可求解的,因此需要求解θ和q(z),当q(z)确定后信息熵H[q(z)]就随之确定。
up主还提到EM的变种,由于很多东西都不了解,因此省略了这部分,见谅。
END