聚类算法：KMeans vs DBSCAN

在数据科学和机器学习中，我们会遇到非常多没有标签的数据，要对这些数据进行分析，就需要用到无监督学习中非常常见的方法——聚类。通过聚类，可以把具有相同特质的数据归并在一起，聚类算法中最常见的就是KMeans和DBSCAN。

K均值聚类（K-means Clustering）

KMeans 是一种基于距离的聚类算法，将距离比较近的数据点看作相似的点，将它们归为一类。

KMeans 具体过程如下：

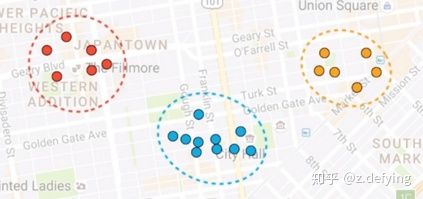
1、比如下面是随机的一些点，我们想将这些点分成三类，聚类中用簇（cluster）表示，那么离得比较近的点肯定归为一个簇，最理想的情况就是如下所示，不同簇用不同的颜色表示。

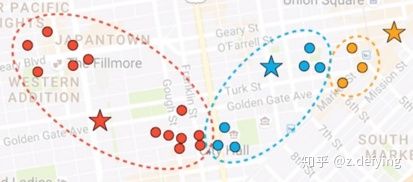
2、我们当然可以通过眼睛看来决定哪些点为一个簇，但是计算机不能，那么我们需要先进行初始化，即随机选三个点分别作为三个簇的中心，也就是质心，如下图的五角星。然后计算每个点到这三个质心的距离，将这些点分配给离它最近的质心。

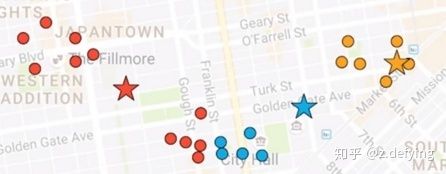
3、现在每个点都有所属的簇了，然后根据每个簇中的所有点重新计算簇的质心（一般是计算平均值），可以看到三个五角星的位置发生了变化。

4、然后又计算每个点到三个新的质心的距离，又将这些点和离它最近的质心归为一类，这些点的所属类别就发生了变化。不断迭代这个过程，直到质心的位置基本不变。

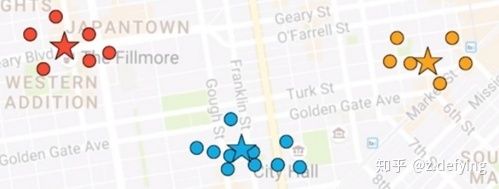
最终的结果就可能如下图所示：

最刚开始的中心点是随机指定的，而中心点不同的指定方法，会使得聚类算法运行的最终结果有很大的不同。我们通常是进行多次初始化，多次运行聚类算法，取最好的那个结果。

KMeans 聚类算法有三个缺点：

• 第一个就是对簇的数量的选择，我们希望指定一个簇数K，以使每个点和其最近的簇的距离之和最小。但是在实际情况中，我们很难找到一个合适的K值，因为我们不知道应该将数据分为几类。
• Kmeans 算法会把所有的数据点都进行分类，但是很多情况下，会有一些离群点，这些点应该被剔除的，但是 Kmeans 算法还是会把它们归为某一类。
• k均值聚类假设对每个簇来说，所有的方向都同等重要。这也就意味着k均值聚类主要适用于球形分布的数据，对于其他分布的数据分类可能不好。

对于 KMeans 聚类的这些缺点，有没有什么更好的算法呢？都这么问了，肯定是有的，那就是 DBSCAN 聚类算法。

DBSCAN 聚类

DBSCAN 全称为 Density-Based Spatial Clustering Algorithm with Noise，基于密度的噪声空间聚类算法。

DBSCAN 算法是基于密度对数据点进行处理的，主要是将特征空间中足够密集的点划分为同一个簇，簇的形状可以是任意的，而且数据点中有噪声点的话，不会将这些点划分给某个簇。

这个算法有几个值得一提的地方：

1、不需要我们指定数据集中簇的个数K。

2、前面说K均值聚类通常只在球形分布的数据集上分类效果比较好，而 DBSCAN 聚类则可以用于各种复杂形状的数据集。

3、可以识别出不属于任何簇的离群点，非常适合用来检测离群点。

DBSCAN 算法是基于密度的算法，所以它将密集区域内的点看作核心点（核心样本）。主要有两个参数：min_samples和eps。

eps表示数据点的邻域半径，如果某个数据点的邻域内至少有min_sample个数据点，则将该数据点看作为核心点。

如果某个核心点的邻域内有其他核心点，则将它们看作属于同一个簇。

如果将eps设置得非常小，则有可能没有点成为核心点，并且可能导致所有点都被标记为噪声。如果将eps设置为非常大，则将导致所有点都被划分到同一个簇。

如果min_samples设置地太大，那么意味着更少的点会成为核心点，而更多的点将被标记为噪声。

DBSCAN 算法也不是万能的，它也有一些缺点：

• DBSCAN 算法的运行速度要比 KMeans 算法慢一些。
• DBSCAN 算法的两个参数也是要根据具体的数据情况进行多次尝试。
• 对于具有不同密度的簇，DBSCAN 算法的效果可能不是很好。

我们来看 DBSCAN 算法的一个例子：

from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# cluster the data into five clusters
dbscan = DBSCAN(eps=0.123, min_samples = 2)
clusters = dbscan.fit_predict(X_scaled)

# plot the cluster assignments
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap="plasma")
plt.xlabel("Feature 0")
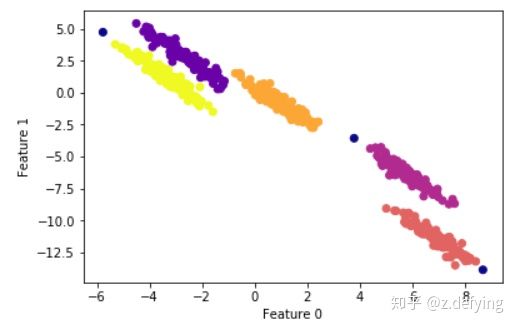
plt.ylabel("Feature 1")

输出结果图为：

通过调整min_samples和eps两个参数，可以将上面的点分为五类，蓝色的点表示离群点。

还可以通过对数据的各个特征进行归一化，使其具有相似的范围，从而更容易找到合适的eps 。

参考：

Data distributions where Kmeans clustering fails Can DBSCAN be a solution?

DBSCAN: What is it? When to Use it? How to use it.

Visualizing DBSCAN Clustering