投影定位算法matlab,浅识——后向投影成像算法（BackProjection，BP) 【MATLAB代码分析】...
一、什么是BP算法
由来：BP算法最初是McCorkle受计算机层析技术的启发推导而来，所谓的计算机层析：就是CT(Computer Tomograpy)，这是在医院中再普遍不过的技术了。
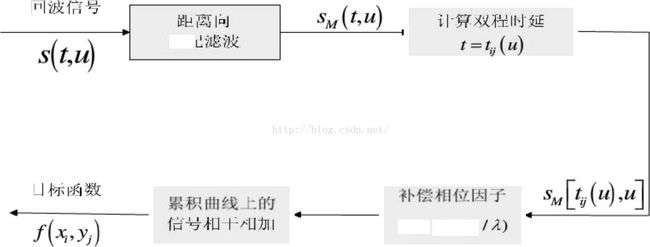
BP算法的原理：BP算法参考了“时延-叠加”的思想，在雷达应用中，其对雷达接收天线接收到的回波信号进行距离向匹配率，获取回波数据中包含的相幅信息，再通过IFFT进行逆傅里叶变换，获取收发天线组合的时延，最后累积信号相干相加得到目标函数。
1.1 BP算法
回波信号与参与电信号进行匹配滤波后，获得的距离压缩输出信号可表示为：
src(h)=Aexp{-j4pf0R(h)/c}
其中，A表示幅度；f0表示载波频率；R( 表示雷达至点目标的距离h)/
二：BP成像算法在SAR中的应用
2.1 优缺点分析：
BP算法有一独到的有点，其可以应用于多种架构的雷达天线而不受阵列形式的限制，这也使得其在雷达应用中显得举足轻重。
另一方面，BP算法也有着巨大的缺陷，其运算数据量比较大，存在冗余的现象，这直接导致了其计算效率低下(在作者仿真BP算法对点目标进行成像的时候就发现需要等待的时间特别长，后文中将具体详述，附图+源代码)。
2.2 FAST-BP算法的特点
在双站合成孔径雷达(Synthetic Aperture Radar,SAR)中,BP算法通过将雷达回波数据反向投影到成像区域的各个像素，像素值通过计算雷达回波在雷达天线和图像像素之间的距离的延时来进行成像。
目前相关提升BP算法速度的研究成果不是很显著，但是在相关文献上还是可以看到一些相应的快速BP算法，这些算法的大致有已下几种套路：
1) 深究算法结构，从理论层面对公式进行简化，优化运算中可以改进的变换，保质保量。
2) 做出一些精确度上的牺牲，通过允许系统上误差来对经典BP算法进行修改或近似，比如西电李浩林研究的“机载SAR快速后向投影算法”，国防科技大学电工院发表的《多级多分辨快速后向投影成像算法》文章。
3) 基于子模块或域分割的简化算法，就是通过大化小的思想把成像区域分成一块块，从总体上降低算法结构的复杂度。
这个作者没有进行深究，读者有兴趣可自行查阅相关资料进行思考。欢迎评论区拍砖切磋！
三、单站SAR的BP算法仿真
》》在这一段作者将尽全力对matlab源码进行附：解释
————在这一段作者将尽力随MATLAB源码进行详细的附：释
3.1 单站SAR
首先作者先以单站SAR为例，这个资料比较齐全，解释起来容易的多。参考教材《合成孔径雷达与成像——算法与实现》一书。(主要还是作者太懒了，不想自己画，而且CSDN编辑器确实难用了点
)
执行步骤：
(注明：图取自网络，示意用)
实例：目标场景
好了，大伙就将就看哈，如上图所示。
工作参数：成像区域网格:2^8&2^10(非严格尺寸，意思是对的。注明：图取自网络，示意用)
运算时间：~4min~(欠火候)
成像区域范围:A到左边缘20m,C到右边缘20m；
》》》》》上边缘纵坐标50m，下边缘纵坐标-50m
3.2 图及matlab源码(关键部分详述，有问题请在评论区咨询)
有魔气！ ! ! ! -_-hahah
clear all; %清除工作空间的内容
%MATLAB有个基本的工作空间，用base标识，此外，当打开一个函数m文件时，可能会产生很多工作空间。
%每一个函数对应一个工作空间。例如，一个图形用户界面程序test，可能有test、gui_mainfcn、
%pushbutton1_callback等工作空间。这时，如果调用clear命令时，需要注意了：%
clc;%清除命令窗口内容
% clc命令是用来清除命令窗口的内容，这点不用多说。% 不管开启多少个应用程序，命令窗口只有一个，所以clc无论是
% 在脚本m文件或者函数m文件调用时，clc命令都会清除命令窗口的内容。clear;
%fmin=？; %请读者自行赋值%fmax=？; %请读者自行赋值
c=3e8; M=901;
kmin=2*fmin/c; %波数
B=2*(fmax-fmin)/c; %带宽
f_step=fmax-fmin/M-1; %步进频率，步进频的好处在于雷达发射此形式信号可以得到目标在各频点的幅度和相位信息R0=10; %希望在评论区看到读者的答案！！
R_v=1.5; %希望在评论区看到读者的答案
rx1=-0.4; %希望在评论区看到读者的答案
rx2=36; %希望在评论区看到读者的答案
rx3=0; %希望在评论区看到读者的答案
rx4=0.9; %希望在评论区看到读者的答案
rx5=0.3; %希望在评论区看到读者的答案
N=161;
angle_step=0.1; %角度最小分量
for n=1:N;
sita=(n-(N+1)/2)*angle_step*pi/180; %sita值表示：
R1(1,n)=sqrt(R0^2+rx1^2-2*R0*rx1*cos(sita+pi/2)); %求一个神奇公式的平方根，
R2(1,n)=sqrt(R0^2+rx2^2-2*R0*rx2*cos(sita+pi/2));
R3(1,n)=sqrt(R0^2+rx3^2-2*R0*rx3*cos(sita+pi/4));
R4(1,n)=sqrt(R0^2+rx4^2-2*R0*rx4*cos(sita));
R5(1,n)=sqrt(R0^2+rx5^2-2*R0*rx5*cos(sita+pi/4));
endfor m=1:M
k=2*pi*(8e9+(m-1)*f_step)/c;
% E(1:N,m)=exp(-2j*k*(R1(1,:)))./R0+exp(-2j*k*(R2(1,:))).
%/R0+exp(-2j*k*(R3(1,:)))./R0+exp(-2j*k*(R4(1,:)))./R0+exp(-2j*k*(R5(1,:)))./R0;
% E(1:N,m)=exp(-2j*k*(R1(1,:)))./R1(1,:);
E(1:N,m)=exp(-2j*k*(R1(1,:)))./R1(1,:)+exp(-2j*k*(R2(1,:)))./R0;
endfor n=1:N
E1(n,:)=ifft(E(n,:)); %求逆傅里叶变换
end
Lt=(0:900)/B;
plot(Lt,abs(E1(81,:)));
F=4;
MF=F*(M-1)+1;
N1=round((R0-R_v)*B*F);
N2=round((R0+R_v)*B*F);
D_N=N2-N1+1;for n=1:N % per det_sita
for m=1:M % per det_f
G(1,m)=(B*(m-1)./(M-1)+kmin).*E(n,m)*( 0.54-0.46.*cos(2*pi*m/M) );%fHamming;对矩阵的每行用fHamming进行加权。
end
P_sita(n,:)=ifft(G(1,1:M),MF);
P_sita1(n,1:D_N)=P_sita(n,N1:N2); % 截取目标区
end
dx=0.005;
dy=dx;
DN=floor(sqrt(2)*R_v/dx);Fig=zeros(DN,DN);
h=waitbar(0,'计算中....'); %由于BP算法计算效率低下，所以特意加了进度条一方读者长时间看不到出图误以为程序出错
for xn=1:DN
xxn=(xn-(DN+1)/2)*dx;
for yn=1:DN
yyn=(yn-(DN+1)/2)*dy;
for n=1:N
sita=(n-(N+1)/2)*angle_step*pi/180;
ham=0.54-0.46*cos(2*(n-1)*pi/(N-1)); %汉明窗
L0=sqrt(R0.^2+xxn.^2+yyn.^2+2*R0*(yyn*cos(sita)-xxn*sin(sita)))-R0; %中场
% L0=yyn*cos(sita)-xxn*sin(sita); % 远场
LB=L0*B*(MF/M)+D_N/2+1;
d_L=LB-floor(LB);
P_L=P_sita1(n,floor(LB))+d_L*(P_sita1(n,floor(LB)+1)-P_sita1(n,floor(LB)));
Fig(xn,yn)=Fig(xn,yn)+P_L*exp(i*2*pi*kmin*L0)*ham;
end
end
waitbar(xn/DN,h);
end
close(h)
x=(1-(DN+1)/2)*dx:dx:(DN-(DN+1)/2)*dx;
y=x;figure;surf(x,y,abs(Fig));shading flat;%shading 是用来处理色彩效果的，分以下三种：
%no shading 一般的默认模式 即shading faceted
%shading flat 在faceted的基础上去掉图上的网格线
%shading interp 在flat的基础上进行色彩的插值处理，使色彩平滑过渡
xlabel('X');ylabel('Y');
转载请注明来源，么么哒！原创声明：本文为-Sure-原创作品，转载时请注明“转自-Sure-”及原文链接。
感谢各位读者的支持，作者会努力提高博客水准，欢迎读者对错误或有待改进的地方提出建议和意见 ——》》PS《《——话说现在写博客花的时间越来越多了，好费时间
！小硕，努力积累一点一滴。
原文：http://blog.csdn.net/u013346007/article/details/51333348