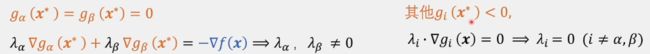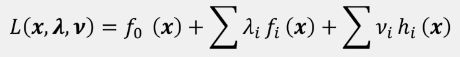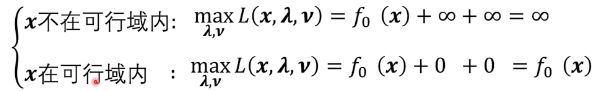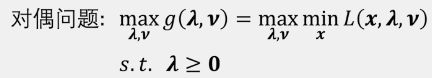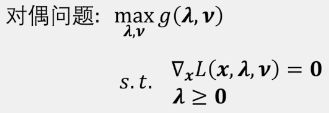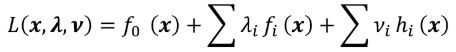拉格朗日对偶问题
一、直观理解拉格朗日乘数法
- 只有一个约束条件
能发现,只有当目标函数f(x, y)的梯度方向和约束条件的梯度方向相反时,通过调整 λ \lambda λ才可以使拉格朗日函数对x和y的偏导为0
- 有多个约束条件
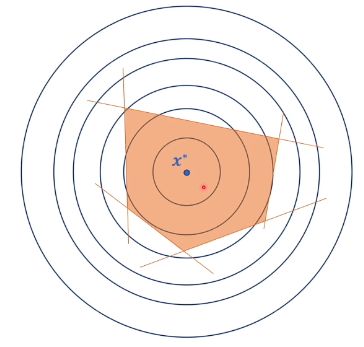
真正起贡献的梯度其实只有其中两个约束条件的梯度,最后的式子变为下式:
所有的 λ i \lambda_i λi都是大于等于0的:
- 如果 λ i = 0 \lambda_i=0 λi=0,那么对应的约束条件 g i ( x ) g_i(x) gi(x)是松弛的(约束条件 g i ( x ) g_i(x) gi(x)没有起到作用)
- 如果 λ i > 0 \lambda_i\gt0 λi>0,那么对应的约束条件 g i ( x ) g_i(x) gi(x)是紧致的(约束条件 g i ( x ) g_i(x) gi(x)起了作用)
- 目标函数的最小值在可行域内
此时,所有的约束条件都是松弛的
二、拉格朗日乘数法的不足
求出来的点不一定是最值,有可能是极值或者鞍点
什么时候极值是最值呢?
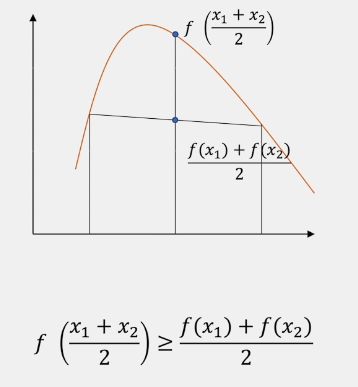
目标函数是凸函数的时候很有可能是最值
如何解决非凸问题?
求原问题的对偶函数
三、拉格朗日对偶问题
目标函数及其约束条件:
拉格朗日函数:
求 L ( x , λ , μ ) L(x,\lambda,\mu) L(x,λ,μ)的最小值可以分成两步,先把 x x x看作常量、 λ \lambda λ和 μ \mu μ看作变量,求 L ( x , λ , μ ) L(x,\lambda,\mu) L(x,λ,μ)的最大值,再在这个最大值的基础上以 x x x为变量求 L ( x , λ , μ ) L(x,\lambda,\mu) L(x,λ,μ)的最小值:
该原问题可以和刚开始求 min f 0 ( x ) \min f_0(x) minf0(x)等价,证明如下:
具体解释就是:
-
当x在可行域内时,显然 ∑ μ i h i ( x ) = 0 \sum\mu_ih_i(x)=0 ∑μihi(x)=0,对任何i来说, ∑ λ i f i ( x ) \sum\lambda_if_i(x) ∑λifi(x)恒小于等于0,它们的最大值也只是0
-
当x不在可行域内时, ∑ λ i f i ( x ) \sum\lambda_if_i(x) ∑λifi(x)的最大值可以取到无穷大(KaTeX parse error: Undefined control sequence: \and at position 13: \lambda\gt0 \̲a̲n̲d̲ ̲f_i(x)>0), ∑ μ i h i ( x ) \sum\mu_ih_i(x) ∑μihi(x)的最大值也可以取到无穷大( μ i \mu_i μi没要求, h i ( x ) ≠ 0 h_i(x)\neq 0 hi(x)=0),求这些无穷大没意义,因为最后要求最小值,无穷大肯定是不要的
所以:
对偶函数:先把 λ \lambda λ和 μ \mu μ看作常量、 x x x看作变量,求 L ( x , λ , μ ) L(x,\lambda,\mu) L(x,λ,μ)的最小值,再在这个最小值的基础上以 λ \lambda λ和 μ \mu μ为量求 L ( x , λ , μ ) L(x,\lambda,\mu) L(x,λ,μ)的最大值:
其实就是颠倒了一下两者的顺序,对偶问题还有另一种形式:
3.1 对偶问题的特性
无论原问题是什么,它的对偶问题都是凸问题!
解释:
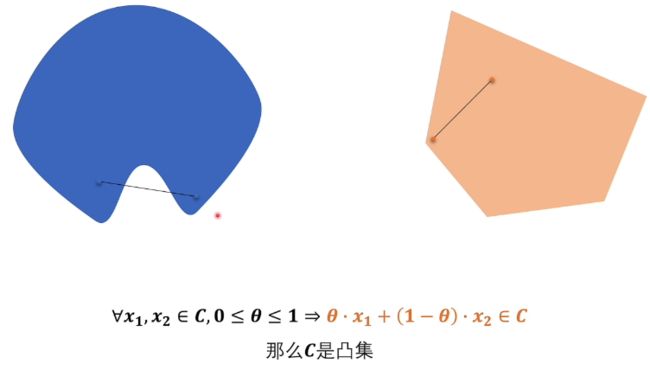
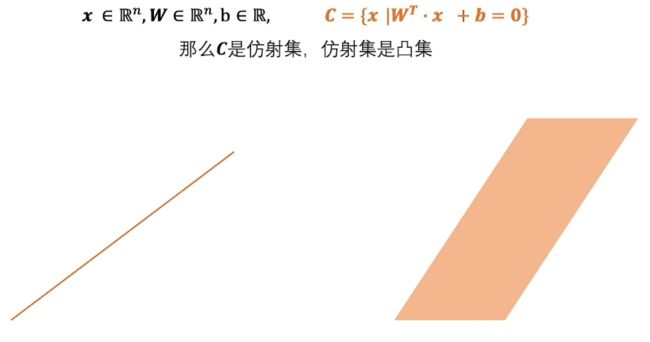
- 凸集、凸函数等概念
- 拉格朗日对偶问题为什么是凸问题?
凸集、凸函数、凸优化等概念
图2还可以这样表示
- 凸集的交集也是凸集
| 维度 | 交集 |
|---|---|
| 1 |  |
| 2 | 线 |
| 3 | 平面 |
| 4 | 立体图形 |
一个问题的目标函数是一个凸函数,可行域是一个凸集,那么这个问题就是一个凸优化问题
3.2 拉格朗日对偶问题为什么是凸问题?
当x确定的时候,假设x*是对偶函数的最优解,
则有:
可以看到:
- 变量 λ \lambda λ和 μ \mu μ都是一阶线性的,目标函数为凸函数
- 拉格朗日对偶问题的约束是 λ i ≥ 0 \lambda_i\ge0 λi≥0,所以它的可行域也是一个凸集
因此:
所以对偶问题一定是凸问题,又因为求的是对偶函数的最大值,所以对偶函数是一个凹函数(凹函数加个负号就是凸函数,注意区分对偶函数和对偶问题的概念)
原问题和对偶问题是否等价?
不一定!
3.3 原问题和对偶问题的等价讨论
拉格朗日函数:
原问题:
对偶问题:
可通过下述推导得到结论:对偶问题的解是原问题的下确界
证明具体看视频吧,理解的不是很透彻
弱对偶关系:P* > D*
强对偶关系:P* = D*
3.4 判断一个问题和它的对偶问题是不是强对偶关系 —— Slater条件(充分条件)
对一个凸优化问题,
存在一个点 x ∈ r e l i n t D x\in relint\space D x∈relint D
使得 f i ( x ) < 0 f_i(x)\lt 0 fi(x)<0,其中 i = 1 , 2 , 3 , . . . , m , A x = b i=1,2,3,...,m,\space Ax = b i=1,2,3,...,m, Ax=b
( r e l i n t D relint D relintD表示可行域的相对内部,及x不在边界上)
则该问题一定是一个强对偶关系的问题
3.5 只要是强对偶关系的问题,一定满足KKT条件(必要条件)
对一个凸优化问题,
互补松弛条件的理解见前面关于 λ i \lambda_i λi和 g i ( x ) g_i(x) gi(x)的松弛和紧致关系
参考视频
“拉格朗日对偶问题”如何直观理解?“KKT条件” “Slater条件” “凸优化”打包理解_哔哩哔哩_bilibili