深度学习PyTorch笔记（13）：多层感知机

这是《动手学深度学习》（PyTorch版）（Dive-into-DL-PyTorch）的学习笔记，里面有一些代码是我自己拓展的。

其他笔记在专栏 深度学习 中。

这并不是简单的复制原文内容，而是加入了自己的理解，里面的代码几乎都有详细注释！！！

7 多层感知机

7.1 隐藏层

在网络中加入一个或多个隐藏层来克服线性模型的限制， 使其能处理更普遍的函数关系类型。
最简单的方法是将许多全连接层堆叠在一起。 每一层都输出到上面的层，直到生成最后的输出——多层感知机（multilayer perceptron，MLP）:

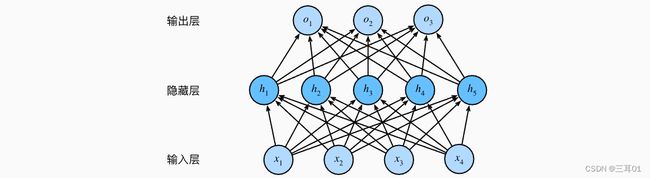
• 输入：$\mathbf{X}\in {\mathbb{R}}^{n\times d}，$表示$n$个样本的小批量，每个样本具有$d$个输入(特征)。
• 中间层：$\mathbf{H}\in {\mathbb{R}}^{n\times h}$，单隐藏层，有$h$个隐藏单元，称为隐藏表示（hidden representations）。
  在数学或代码中，$\mathbf{H}$也被称为隐藏层变量（hidden-layer variable）或隐藏变量（hidden variable）。
• 因为隐藏层和输出层都是全连接的，所以我们具有隐藏层权重${\mathbf{W}}^{(1)}\in {\mathbb{R}}^{d\times h}$和隐藏层偏置${\mathbf{b}}^{(1)}\in {\mathbb{R}}^{1\times h}$；
  输出层权重${\mathbf{W}}^{(2)}\in {\mathbb{R}}^{h\times q}$和输出层偏置${\mathbf{b}}^{(2)}\in {\mathbb{R}}^{1\times q}$。
• 输出：$\mathbf{O}\in {\mathbb{R}}^{n\times q}$，按如下方式计算：
  $$\begin{array}{rl}\mathbf{H}& =\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)},\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}.\end{array}$$

此时仍然是线性的，需要在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）$\sigma$，激活函数的输出被称为活性值（activations），这样就发挥了多层架构的潜力：
$$\begin{array}{rl}\mathbf{H}& =\sigma (\mathbf{X}{\mathbf{W}}^{(1)}+{\mathbf{b}}^{(1)}),\\ \mathbf{O}& =\mathbf{H}{\mathbf{W}}^{(2)}+{\mathbf{b}}^{(2)}.\end{array}$$
通过使用更深（而不是更广）的网络，我们可以更容易地逼近许多函数。

7.2 激活函数（activation function）

激活函数通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。

7.2.1 ReLU函数（修正线性单元Rectified linear unit，ReLU）

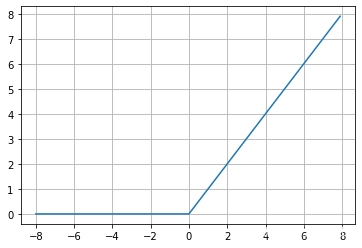
给定元素$x$，ReLU函数被定义为该元素与$0$的最大值：
$$\mathrm{ReLU}(x)=\max (x,0).$$

%matplotlib inline
import torch
import matplotlib.pyplot as plt

x = torch.arange(-8, 8, 0.1, requires_grad=True)
y = torch.relu(x)
plt.plot(x.detach(), y.detach())
plt.grid()

梯度：

• 如果用y.backward()会报错，因为此时y不是标量，需要传入一个与out同形的Tensor，即torch.ones_like(x)，详细说明。
• 下文中retain_graph=True的作用：进行一次backward之后，各个节点的值会清除，这样进行第二次backward会报错，如果加上retain_graph==True后,可以再来一次backward。

y.backward(torch.ones_like(x), retain_graph=True)
plt.plot(x.detach(), y.detach())
plt.grid()

7.2.1.1 pReLU

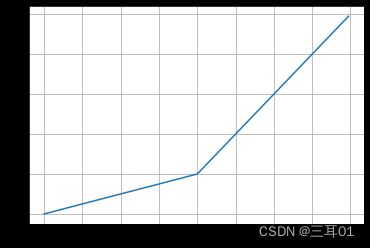
ReLU函数有许多变体，包括参数化ReLU（Parameterized ReLU，pReLU）函数。该变体为ReLU添加了一个线性项，因此即使参数是负的，某些信息仍然可以通过：
$$\mathrm{pReLU}(x)=\max (0,x)+\alpha \min (0,x).$$

x = torch.arange(-8, 8, 0.1, requires_grad=True)

def prelu(x, alpha):
    x_like_zero = torch.zeros_like(x)
    y = torch.relu(x) + alpha * torch.min(x, x_like_zero)
    return y
    
y = prelu(x, 0.25)
plt.plot(x.detach(), y.detach())
plt.grid()

y.backward(torch.ones_like(x), retain_graph=True)
plt.plot(x.detach(), x.grad)
plt.grid()

7.2.2 sigmoid函数（挤压函数，squashing function）

将范围(-inf, inf)中的任意输入压缩到区间(0, 1)中的某个值：
$$\mathrm{sigmoid}(x)=\frac{1}{1+\exp (-x)}.$$

sigmoid函数是一个平滑的、可微的阈值单元近似。 当我们想要将输出视作二元分类问题的概率时， sigmoid仍然被广泛用作输出单元上的激活函数 （可以将sigmoid视为softmax的特例）。
然而，sigmoid在隐藏层中已经较少使用， 它在大部分时候被更简单、更容易训练的ReLU所取代。

x = torch.arange(-8, 8, 0.1, requires_grad=True)
y = torch.sigmoid(x)
plt.plot(x.detach(), y.detach())
plt.grid()

sigmoid函数的导数为下面的公式：
$$\frac{d}{dx}\mathrm{sigmoid}(x)=\frac{\exp (-x)}{(1+\exp (-x){)}^2}=\mathrm{sigmoid}(x)\left(1-\mathrm{sigmoid}(x)\right).$$

y.backward(torch.ones_like(x), retain_graph=True)
plt.plot(x.detach(), x.grad)
plt.grid()

7.2.3 tanh函数(双曲正切)

与sigmoid函数类似，tanh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上：
$$\tanh (x)=\frac{1-\exp (-2x)}{1+\exp (-2x)}.$$

函数的形状类似于sigmoid函数， 不同的是tanh函数关于坐标系原点中心对称：

x = torch.arange(-8, 8, 0.1, requires_grad=True)
y = torch.tanh(x)
plt.plot(x.detach(), y.detach())
plt.grid()

当输入接近0时，tanh函数的导数接近最大值1。 与我们在sigmoid函数图像中看到的类似， 输入在任一方向上越远离0点，导数越接近0：

y.backward(torch.ones_like(x), retain_graph=True)
plt.plot(x.detach(), x.grad)
plt.grid()

7.2 多层感知机的从零开始实现

torch.nn库的说明
继续使用Fashion-MNIST图像分类数据集：

7.2.1 数据读取

import torch
from torch import nn 
import torchvision
from torchvision import transforms
from torch.utils import data

batch_size = 256

"""获取和读取Fashion-MNIST数据集"""
def load_data_fashion_mnist(batch_size):
    trans = transforms.Compose([transforms.ToTensor()])  # transforms.Compose将多个转换函数组合起来使用，转换为张量
    mnist_train = torchvision.datasets.FashionMNIST(
        root="C:/Users/xinyu/Desktop/myjupyter/data", 
        train=True, 
        transform=trans, 
        download=False)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="C:/Users/xinyu/Desktop/myjupyter/data", 
        train=False, 
        transform=trans, 
        download=False)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True, num_workers=4),
           data.DataLoader(mnist_test, batch_size, shuffle=False, num_workers=4))

train_iter, test_iter = load_data_fashion_mnist(batch_size)

# i=0
# for X, y in train_iter:
#     print(X.shape, y.shape)  # torch.Size([256, 1, 28, 28]) torch.Size([256])
#     print(y)
#     i+=1  # 235次循环，最后一次不是256
# print(i)

# i=0
# for X, y in test_iter:
#     print(X.shape, y.shape)
#     i+=1  # 40次循环，最后一次不是256
# print(i)

7.2.2 初始化模型参数

每个图像由 28*28=784 个灰度像素值组成。 所有图像共分为10个类别。 忽略像素之间的空间结构， 我们可以将每个图像视为具有784个输入特征 和10个类的简单分类数据集。
因此，我们实现一个具有单隐藏层的多层感知机， 它包含256个隐藏单元（可以将这两个变量都视为超参数）。
通常，选择2的若干次幂作为层的宽度。 因为内存在硬件中的分配和寻址方式，这么做往往可以在计算上更高效。

num_inputs, num_hiddens, num_outputs = 784, 256, 10

W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

7.2.3 激活函数

很简单，就用relu：

def relu(x):
    a = torch.zeros_like(x)
    return torch.max(a, x)

7.2.4 模型

def mlp_net(x):
    x = x.reshape((-1, num_inputs))  # torch.Size([256, 784])
    h = torch.mm(x, W1) + b1  # torch.Size([256, 256])
    h_relu = relu(h)  # torch.Size([256, 256])
    y_hat = torch.mm(h, W2) + b2  # torch.Size([256, 10])
    return y_hat

7.2.5 损失函数

loss = nn.CrossEntropyLoss()
# x = torch.randn(256,10)  # 小数
# y1 = torch.randint_like(y, 0, 9)  # 整数,torch.Size([256])
# loss(x,y), loss(x,y).sum()  # 可以得出结果，两边结果一样

7.2.6 训练

epochs, lr = 10, 0.1
optimizer = torch.optim.SGD(params, lr=lr)

a=0
def mlp_train(mlp_net, train_iter, test_iter, loss, epochs, batch_size, params=None, lr=None, optimizer=None):
    for epoch in range(epochs):
        train_loss_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            # print(y.shape) # torch.Size([256])
            y_hat = mlp_net(X)  # torch.Size([256, 10])
            mlp_loss = loss(y_hat, y)
#             optimizer.zero_grad()
            
            # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
                    
            mlp_loss.backward()
#             optimizer.step()
            if optimizer is None:
                SGD(params, lr, batch_size)
            else:
                optimizer.step()  # “softmax回归的简洁实现”一节将用到
            
            train_loss_sum += mlp_loss.item()  # .item()转换为标量
            train_acc_sum += (y_hat.argmax(dim=1) == y).sum().item()  # .item()将Tensor变量转换为python标量（int float等）
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter, mlp_net)
        print("epoch: {}, loss: {:.4f}, train acc: {:.3f}, test acc: {:.3f}".format(
            epoch, train_loss_sum / n, train_acc_sum / n, test_acc))    
            
            
def evaluate_accuracy(test_iter, mlp_net):
    acc_sum, n = 0.0, 0
    for X, y in test_iter:
        acc_sum += (mlp_net(X).argmax(dim=1) == y).float().sum().item()
        n += y.shape[0]
    return acc_sum / n
                
mlp_train(mlp_net, train_iter, test_iter, loss, epochs, batch_size, params, lr, optimizer)

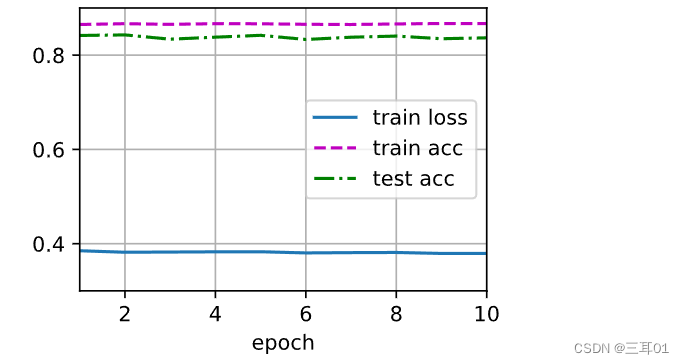
emmm好像有哪里出了问题的样子，最后的结果：

epoch: 0, loss: 0.0015, train acc: 0.863, test acc: 0.810
epoch: 1, loss: 0.0015, train acc: 0.864, test acc: 0.834
epoch: 2, loss: 0.0015, train acc: 0.864, test acc: 0.815
epoch: 3, loss: 0.0015, train acc: 0.863, test acc: 0.845
epoch: 4, loss: 0.0015, train acc: 0.864, test acc: 0.828
epoch: 5, loss: 0.0015, train acc: 0.864, test acc: 0.831
epoch: 6, loss: 0.0015, train acc: 0.866, test acc: 0.817
epoch: 7, loss: 0.0015, train acc: 0.865, test acc: 0.838
epoch: 8, loss: 0.0015, train acc: 0.865, test acc: 0.844
epoch: 9, loss: 0.0015, train acc: 0.866, test acc: 0.838

图大概长这样：

7.3 MLP的简洁实现

import torch
from torch import nn

mlp_net = nn.Sequential(nn.Flatten(),
                       nn.Linear(784, 256),
                       nn.ReLU(),
                       nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

mlp_net.apply(init_weights);

batch_size, lr, num_epochs = 256, 0.1, 10
loss = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(mlp_net.parameters(), lr=lr)

train_iter, test_iter = load_data_fashion_mnist(batch_size)
mlp_train(mlp_net, train_iter, test_iter, loss, epochs, batch_size, params, lr, optimizer)

epoch: 0, loss: 0.0041, train acc: 0.639, test acc: 0.719
epoch: 1, loss: 0.0023, train acc: 0.793, test acc: 0.803
epoch: 2, loss: 0.0020, train acc: 0.819, test acc: 0.813
epoch: 3, loss: 0.0019, train acc: 0.833, test acc: 0.828
epoch: 4, loss: 0.0018, train acc: 0.840, test acc: 0.795
epoch: 5, loss: 0.0017, train acc: 0.847, test acc: 0.826
epoch: 6, loss: 0.0016, train acc: 0.853, test acc: 0.847
epoch: 7, loss: 0.0016, train acc: 0.858, test acc: 0.833
epoch: 8, loss: 0.0015, train acc: 0.862, test acc: 0.812
epoch: 9, loss: 0.0015, train acc: 0.863, test acc: 0.844

以后的代码应该不会跟着李沐的书走了，他的代码大量使用了自己的包 d2l，这让我感到很困扰，因为有一些函数并没有在原文给出，而是直接用 d2l 引用，而且直接无脑使用 d2l 也会让人忘记具体如何操作。尤其是当想原封不动使用这里的代码的时候，总会有 d2l。。。