动手学深度学习Pytorch（三）——卷积神经网络

1. 参考资料

[1] 动手学深度学习 v2 - 从零开始介绍深度学习算法和代码实现
课程主页：https://courses.d2l.ai/zh-v2/
教材：https://zh-v2.d2l.ai/
[2] 李沐老师B站视频：https://www.bilibili.com/video/BV1MB4y1F7of?p=3

2. 图像卷积

2.1 互相关运算（cross-correlation）

在卷积层中，输入张量和核张量通过互相关运算产生输出张量。

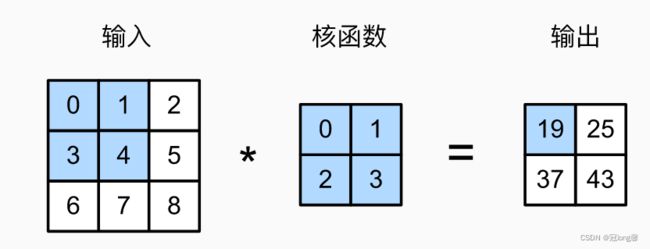
计算： 卷积窗口从输入张量的左上角开始，从左到右从上到下滑动。当卷积窗口滑动到新一个位置时，包含在该窗口的部分张量与卷积张量按元素相乘，得到的值求和得到单一标量值。
$$Y(i,j)=(X(i:i+h,y:y+w)\ast K).sum()$$

作用
卷积层可以通过重复使用卷积核有效地表征局部空间

2.2 学习卷积核

对于连续的卷积层而言，我们不可能手动设计卷积核。我们需要学习有X生成Y的卷积核。
思想
在每次迭代中，比较Y与卷积层输出的平方误差，然后计算梯度更新卷积核。

# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)
# 循环迭代开始
Y_hat = conv2d(X)		# X输入的卷积层输出
l = (Y_hat - Y) ** 2	# 平方误差
conv2d.zero_grad()		# 梯度清零
l.sum().backward()		# 反向传播-自动求导
# 更新卷积核
conv2d.weight.data[:] -= lr * conv2d.weight.grad
# 循环迭代结束

2.3 特征图和感受野

特征图（feature map）
卷积层的输出可以看作输入在空间维度上的表征，称为特征图。

感受野（receptive field）
在卷积神经网络中，对于某一层的任意元素，其感受野是指前向计算的所有可能输入区域。

其中，输出层中19的感受野是输入层中的阴影部分。对输出层与2*2的核函数再做互相干运算，输出单个元素z。z的感受野就是输入层的9个元素。更深的卷积神经网络使特征图中单个元素的感受野更加宽阔。

3. 填充和步幅（padding and stride）

一般来说，假设输入形状$n_h\times n_w$，卷积核窗口形状$k_h\times k_w$，输出形状为：
$$(n_h-k_h+1)\times (n_w-k_w+1)$$

卷积层输出的形状由输入和核窗口形状决定。

• 情况1：连续的卷积之后，得到的输出大小可能太小了，从而丢失了很多原始图像边界上的有用信息。
• 情况2：希望大幅度降低图像大小，则需要采用很多卷积层才能实现。

3.1 填充（padding）

目的
防止在连续卷积后，输出太小而导致的有用信息丢失。

定义
在输入的高和宽两侧填充元素（0）。当设置填充$padding=n$时，两侧一共填充$2n$行（列）。

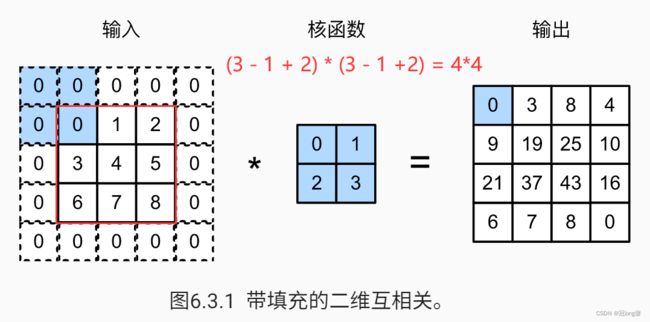
输出形状

• 假设高的两侧一共填充$p_h$行，宽两侧一共填充$p_w$行，则输出形状为：

$$(n_h-k_h+1+p_h)\times (n_w-k_w+1+p_w)$$

• 一般设置$p_h=k_h-1,p_w=k_w-1$使输入和输出具有相同的高和宽。

参数
$padding=(h,w)$：表示总共添加2h行2w列
$padding=x$：表示总共添加2x行2x列

import torch
from torch import nn

conv2d = nn.Conv2d(1, 1, kernel_size = 3, padding = 1)	# 总共添加2行2列

3.2 步幅（stride）

目的
大幅度降低输入大小、高效计算或缩减采样次数

定义
每次滑动元素的数量

输出形状

• 假设垂直步幅为$s_h$，水平步幅为$s_w$，则输出大小为：

$$(n_h-k_h+p_h+s_h)/s_h\times (n_w-k_w+p_w+s_w)/s_w$$

• 一般将高度和宽度步幅设置为2，从而将输入的高度和宽度减半：
  $$n_h/2\times n_w/2$$

参数
$stride=(s_h,s_w)$：高度和宽度的步幅分别为$s_h,s_w$
$stride=s$：高度和宽度的步幅均为s

conv2d = nn.Conv2d(1, 1, kernel_size=(3, 5), padding=(0, 1), stride=(3, 4))

当输入为8*8时，垂直填充0行，水平填充2列，高度步幅为3，宽度步幅为4，输出大小为：
$$(8-3+1+0+3)/3\times (8-5+1+2+4)/4=2\times 2$$

4. 多输入多输出通道

目的

• 每个输出通道可以识别特定模式。
  
• 输入通道核识别并组合输入中的模式。

4.1 多输入通道

假设输入的通道数为$c_i$，那么卷积核的输入通道数也需要为$c_i$
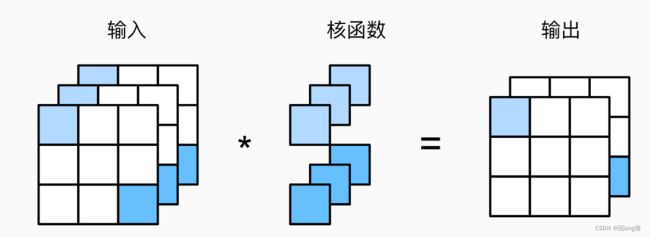
多通道输入和多通道卷积核之间的二维互相关运算
对每个通道输入的二维张量和卷积核的二维张量进行互相关运算，再对通道求和得到二维张量。

• 输入$X$： $c_i\times n_h\times n_w$
• 卷积核$W$：$c_i\times k_h\times k_w$
• 输出$Y$：$m_h\times m_w$
• （多通道卷积求和得到单输出通道）
  $$Y=\sum _{i=0}^{c_i}{X}_{i,:,:}\ast W_{i,:,:}$$

4.2 多输出通道

• 输入$X$： $c_i\times n_h\times n_w$
• 卷积核$W$：$c_o\times c_i\times k_h\times k_w$
• 输出$Y$：$c_o\times m_h\times m_w$
• 可以有多个三维卷积核，每个核生成一个输出通道。
  $$Y_{i,:,:}=\sum _{i=0}^{c_i}X\ast W_{i,:,:,:}$$

4.3 $1\times 1$卷积层

• $k_h=k_w=1$的卷积核。输入形状$n_h{n}_w\times c_i$，卷积层的权重维度为$c_i\times c_o$，输出形状为$n_h\times n_w\times c_o$
  
• $1\times 1$卷积层不识别空间模式，只是融合通道。
  理解：通过$1\times 1$卷积层能将输入通道数为$c_i$的输入层转化为通道数为$c_o$的输出层。

4.4 二维卷积层

• 输入$X$： $c_i\times n_h\times n_w$
• 卷积核$W$：$c_o\times c_i\times k_h\times k_w$
• 偏差$B$：$c_o\times c_i$
• 输出$Y$：$c_o\times m_h\times m_w$
• $Y=X\ast W+B$
• 时间复杂度：$O(c_i{c}_o{k}_h{k}_w{m}_h{m}_w)$

5. 池化层

池化层通常作用于卷积层之后。
目的

• 缓解卷积层对位置的敏感性（卷积对位置敏感）
• 降低对空间降采样表示的敏感度（需要一定程度的平移不变性）

5.1 最大池化层和平均池化层

池化层由一个固定形状的窗口组成，该窗口根据其步幅大小在输入的所有区域上滑动，为池化窗口遍历的每个位置计算一个输出。
（1）最大池化层
返回滑动窗口中的最大值。

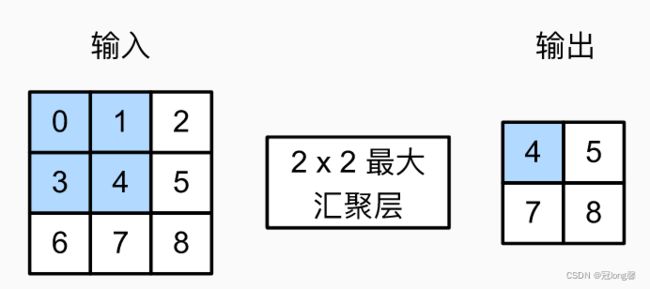
作用

1. 允许输入发生小小的偏移，
2. 检测窗口中最强的模式信号

（2）平均池化层
返回滑动窗口中的平均值。
作用

1. 柔和化

5.2 超参数

• 相同： 池化层与卷积层类似，都具有填充和步幅。
• 填充padding
• 步幅stride
• 区别： 在每个输入通道应用池化层以获得相应的输出通道，输出通道数 = 输入通道。

6. 卷积层的超参数

1. 填充$padding=(p_h,p_w)$
2. 步幅$stride=(s_h,s_w)$
3. 输出通道$c_o$