【动手学深度学习PyTorch版】15 池化层

上一篇请移步【动手学深度学习PyTorch版】14 卷积层里的多输入多输出通道_水w的博客-CSDN博客

目录

一、池化层

1.1 池化层

◼池化层原因

◼ 二维最大池化

1.2 填充、步幅与多个通道

1.3 平均池化层

1.4 总结

二、代码实现池化层

2.1 池化层（使用自定义）

◼ 实现池化层的正向传播

◼ 填充和步幅

◼ 池化层在每个通道上单独运算

---

一、池化层

1.1 池化层

◼池化层原因

卷积层的位置是怎么样保存信息的？

如图所示，输入X为这样，X有一个边缘。那么如果用1X2的卷积核[1,-1]，会使得下图中Y输出的第二列全部为1，其他为0，那么1个像素的偏移移位，就会导致0的输出。

如果像素偏移，会导致边缘检测的1在其他位置输出，所以说卷积对像素的位置是非常敏感的。

这里本质上讲的是池化层对于像素偏移的容忍性。

所以我们有时候会觉得这个不是特别好的一件事，我们需要有一个池化层。

◼ 二维最大池化

池化层主要用于缓解卷积层对位置的过度敏感性。

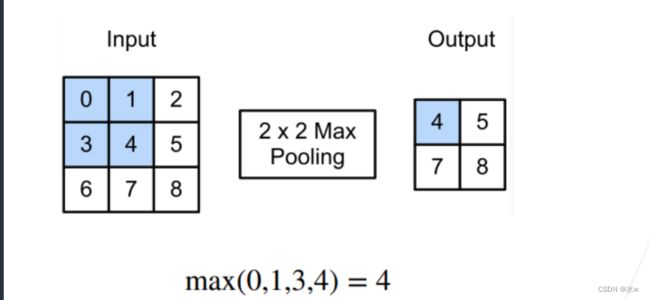
工作原理，与之前的卷积层有点像。同卷积层一样，池化层每次对输入数据的一个固定形状窗口（又称池化窗口）中的元素计算输出，池化层直接计算池化窗口内元素的最大值或者平均值，该运算也分别叫做最大池化或平均池化。下图展示了池化窗口形状为 2×2 的最大池化。

二维平均池化的工作原理与二维最大池化类似，但将最大运算符替换成平均运算符。池化窗口形状为 p×q 的池化层称为 p×q 池化层，其中的池化运算叫作 p×q 池化。

如果再卷积输出上作用一次2X2池化，如下图所示，

图中可以看到，2X2池化是可以容忍输入的一个像素发生小小的一定的偏移。

而且作用在卷积输出上，有一点模糊化的效果，使得输出值的附近的一个小窗口里的值都会出现，这就是最大池化层。

1.2 填充、步幅与多个通道

（1）池化层与卷积层类似，都具有填充和步幅。池化层也可以在输入的高和宽两侧填充并调整窗口的移动步幅来改变输出形状。池化层填充和步幅与卷积层填充和步幅的工作机制一样。

（2）但是池化层与卷积层不一样的地方是：没有可学习的参数K，就是计算最大值；

（3）池化层不会像卷积一样可以融合多个通道，只能在每个输入通道应用池化层以获得相应的输出通道；

（4）在处理多通道输入数据时，池化层对每个输入通道分别池化，但不会像卷积层那样将各通道的结果按通道相加。这意味着池化层的输出通道数与输入通道数相等。-----------输出通道数=输入通道数；

1.3 平均池化层

直观上来讲，最大池化层和平均池化层的区别：

• 最大池化层：输出的是每个窗口中最强的模式信号；
• 平均池化层：将最大池化层中的“最大”操作替换为平均，输出的是每个窗口中平均的模式信号强度，但有一个比较融合化的效果；

1.4 总结

① 二维卷积层可以帮助我们检测图像物体边缘。

② 无论是原始图片，还是经过卷积核处理的中间特征，都是基于像素的基础进行的数学运算。

③ 实际图像里，我们感兴趣的物体不会总出现在固定像素位置：即使我们用三脚架固定相机去连续拍摄同一个物体也极有可能出现像素位置上的偏移。

④ 这会导致同一个物体的边缘对应的输出可能出现在卷积输出中的不同位置，进而对后面的模式识别造成不便。

⑤ 另外，绝大多数计算机视觉任务对图像处理终极目标是识别图片内的物体，所以不需要细致到对每个像素进行检测，只需要找到图片中物体的大概轮廓就好了。

⑥ 池化层可以缓解卷积层对位置的过度敏感性。所以池化层主要用于缓解卷积层对位置的过度敏感性。

二、代码实现池化层

2.1 池化层（使用自定义）

◼ 实现池化层的正向传播

（1）池化层的实现

拿到输入，池化窗口大小参数，

输入的宽/高减去窗口的宽/高，再加上1，这里没有padding和stride。

双层for遍历，先行遍历，再列遍历。

import torch
from torch import nn
from d2l import torch as d2l

# 实现池化层的正向传播
def pool2d(X, pool_size, mode='max'):  # 拿到输入，池化窗口大小
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1)) # 输入的宽/高减去窗口的宽/高，再加上1，这里没有padding和stride
    for i in range(Y.shape[0]): # 行遍历
        for j in range(Y.shape[1]): # 列遍历
            if mode == 'max':    # 最大值
                Y[i,j] = X[i:i + p_h, j:j + p_w].max()
            elif mode == 'avg':    # 均值
                Y[i,j] = X[i:i + p_h, j:j + p_w].mean()
    return Y

（2）验证二维最大池化层的输出

# 验证二维最大池化层的输出
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
print(pool2d(X, (2,2)))

 可以看到，返回的结果与上图的结果一致。

（3）验证平均池化层

# 验证平均池化层
print(pool2d(X, (2,2), 'avg')) 

可以看到，返回的结果相对于二维最大池化层的输出小了很多，因为均值永远是小于等于最大值的。

◼ 填充和步幅

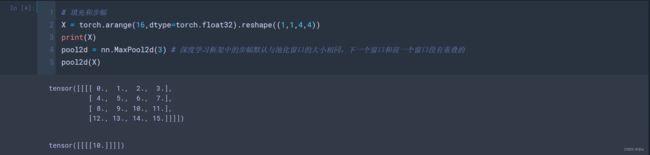
（1）输入和输出通道都为1，简单认为创建了4x4的矩阵，

调用nn.MaxPool2d，深度学习框架中的步幅默认与池化窗口的大小相同，下一个窗口和前一个窗口没有重叠的

# 填充和步幅
X = torch.arange(16,dtype=torch.float32).reshape((1,1,4,4)) 
print(X)
pool2d = nn.MaxPool2d(3) # 深度学习框架中的步幅默认与池化窗口的大小相同，下一个窗口和前一个窗口没有重叠的
pool2d(X)

由于后面的窗口值不够，只会返回前面一个3x3矩阵的值，最大值就是10，所以返回标量。

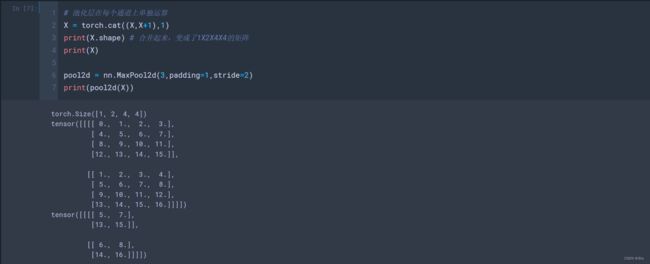
（2）填充和步幅可以手动设定

# 填充和步幅可以手动设定
pool2d = nn.MaxPool2d(3,padding=1,stride=2)
print(pool2d(X))

设定一个任意大小的矩形池化窗口，并分别设定填充和步幅的高度和宽度。

# 设定一个任意大小的矩形池化窗口，并分别设定填充和步幅的高度和宽度
pool2d = nn.MaxPool2d((2,3),padding=(1,1),stride=(2,3))
print(pool2d(X))

 ◼ 池化层在每个通道上单独运算

双通道：X和X+1，合并起来，变成了1X2X4X4的矩阵

# 池化层在每个通道上单独运算
X = torch.cat((X,X+1),1)
print(X.shape) # 合并起来，变成了1X2X4X4的矩阵
print(X)

pool2d = nn.MaxPool2d(3,padding=1,stride=2)
print(pool2d(X))