Chapter1-6_Speech_Recognition(RNN-T Training)
文章目录
-
- 1 一个alignment概率的计算
- 2 所有alignments概率的计算
- 3 Training
- 4 Inference
- 5 小结
本文为李弘毅老师【Speech Recognition - RNN-T Training (optional)】的课程笔记,课程视频youtube地址,点这里(需)。
下文中用到的图片均来自于李宏毅老师的PPT,若有侵权,必定删除。
文章索引:
上篇 - 1-5 Alignment of HMM, CTC and RNN-T
下篇 - 1-7 Language Modeling
总目录
1 一个alignment概率的计算
不管是HMM,还是CTC,还是RNN-T,它们计算得到某一个alignment的概率的方法是一致的。下面以RNN-T为例,来说一下计算的方法。
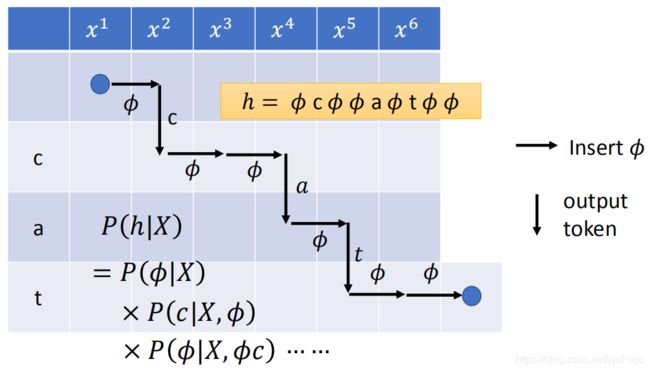
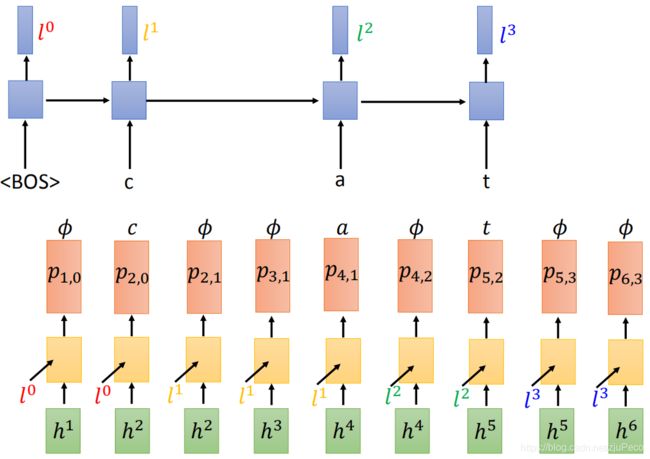
如下图所示,我们现在来计算 h = ϕ c ϕ ϕ a ϕ t ϕ ϕ h=\phi c \phi \phi a \phi t \phi \phi h=ϕcϕϕaϕtϕϕ的概率,写成公式就是
P ( h ∣ X ) = P ( ϕ ∣ X ) P ( c ∣ X , ϕ ) P ( ϕ ∣ X , ϕ c ) ⋯ P(h|X)=P(\phi | X)P(c | X,\phi)P(\phi | X,\phi c) \cdots P(h∣X)=P(ϕ∣X)P(c∣X,ϕ)P(ϕ∣X,ϕc)⋯
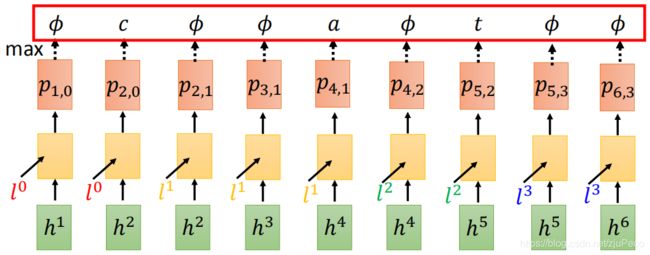
那么这个结合模型到底是怎么算出来的呢?在decode的时候,RNN-T会有两个RNN,一个RNN_1(上半图)会吃一个“ < B O S >
由于我们这次计算的是" ϕ \phi ϕ",根据RNN-T的特性,我们不会去计算RNN_1,而是把新的 h 2 h_2 h2和旧的 l 0 l_0 l0塞进RNN_2当中,吐出一个由 h 2 h_2 h2和 l 0 l_0 l0生成的概率分布 p 2 , 0 p_{2,0} p2,0,从这个 p 2 , 0 p_{2,0} p2,0中找到字符"c"的概率,就得到了 P ( c ∣ X , ϕ ) P(c | X,\phi) P(c∣X,ϕ)。
又因为RNN-T的特性,在没有遇到" ϕ \phi ϕ“不会喂给RNN_2新的 h h h,而 R N N 1 RNN_1 RNN1需要重新计算一个得到 l 1 l_1 l1,于是由 h 2 h_2 h2和 l 1 l_1 l1生成概率分布 p 2 , 1 p_{2,1} p2,1,从中找到” ϕ \phi ϕ"的对应概率,就得到了 P ( ϕ ∣ X , ϕ c ) P(\phi | X,\phi c) P(ϕ∣X,ϕc)。
依此类推,一致计算下去,直到算完整个 h h h。然后把得到的概率值,全都乘起来,就得到了我们的 P ( h ∣ X ) P(h|X) P(h∣X)。
2 所有alignments概率的计算
P ( h ∣ X ) P(h|X) P(h∣X)会算了,接下来,我们要来算一下 P ( Y ∣ X ) P(Y|X) P(Y∣X)。得益于RNN-T有两个结构上不影响的RNN,我们在计算 p i , j p_{i,j} pi,j的时候,不管前面的输出顺序如何,其结果都是保持不变的。比如,在计算 p 4 , 2 p_{4,2} p4,2时,不管前面的输出序列是" ϕ c ϕ ϕ a \phi c \phi \phi a ϕcϕϕa",还是“ c ϕ ϕ a ϕ c \phi \phi a \phi cϕϕaϕ",还是“ ϕ ϕ ϕ c a \phi \phi \phi c a ϕϕϕca",我们的 l 2 l^2 l2和 h 4 h^4 h4是打死不变的,所以 p 4 , 2 p_{4,2} p4,2是不会变的。
不过这里我其实有一个疑惑,虽然 l 2 l^2 l2和 h 4 h^4 h4是不会变的,但是生成 p 4 , 2 p_{4,2} p4,2的这个RNN的记忆不会因为前面产生token的顺序不同而变化吗?存疑。(疑惑已解,生成 p 4 , 2 p_{4,2} p4,2的是简单的DNN,不是RNN,黄色方块没有横向的传播)

现在我们就认为 p i , j p_{i,j} pi,j是不会变化的,然后来看一下下面这个表格。然后我们会用和HMM中的forward algorithm差不多的方法来计算 P ( Y ∣ X ) P(Y|X) P(Y∣X)。
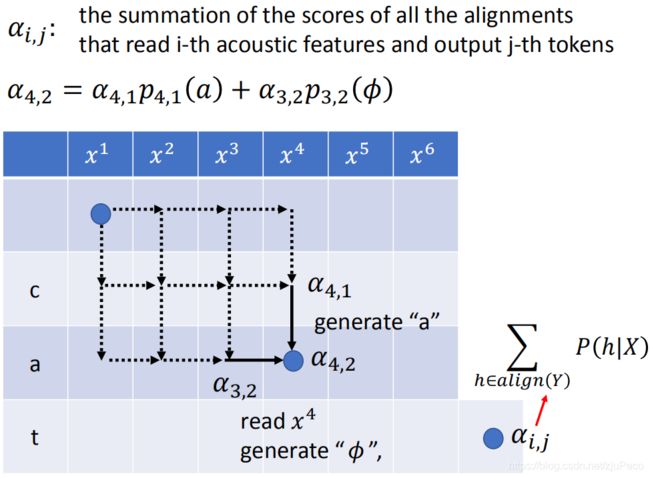
首先我们定义 α i , j \alpha_{i,j} αi,j表示读取了第 i i i个声音讯号的特征并且输出了第 j j j个token时,所有alignments的概率之和。比如 α 4 , 2 \alpha_{4,2} α4,2就表示输出了” c c c“和" a a a",且用到 h 4 h_4 h4时,所有alignments的概率之和。
而 α 4 , 2 \alpha_{4,2} α4,2只可能从 α 4 , 1 \alpha_{4,1} α4,1或者 α 3 , 2 \alpha_{3,2} α3,2过来,所以有
α 4 , 2 = α 4 , 1 p 4 , 1 ( a ) + α 3 , 2 p 3 , 2 ( ϕ ) \alpha_{4,2} = \alpha_{4,1}p_{4,1}(a)+ \alpha_{3,2}p_{3,2}(\phi) α4,2=α4,1p4,1(a)+α3,2p3,2(ϕ)
按照这个办法,我们就可以把这整个表格填满,而右下角最后一个格子的概率,就是 P ( Y ∣ X ) P(Y|X) P(Y∣X)。
3 Training
而以上的这些步骤,都只是一个forward的过程,我们还没有到training这一步。我们先要有一个一组参数 θ \theta θ可以输出 P θ ( Y ^ ∣ X ) P_{\theta}(\hat{Y}|X) Pθ(Y^∣X),然后我们再用梯度下降的方法去优化参数,使得给定一段声音讯号 X X X,模型输出标签 Y ^ \hat{Y} Y^的概率是最大的。
θ ∗ = a r g m a x ⏟ θ l o g P θ ( Y ^ ∣ X ) \theta^* = \underbrace{argmax}_{\theta} log P_{\theta}(\hat{Y}|X) θ∗=θ argmaxlogPθ(Y^∣X)
在梯度下降时,我们当然要先求解一下偏微分
∂ P ( Y ^ ∣ X ) ∂ θ \frac{\partial P(\hat{Y}|X)}{\partial \theta} ∂θ∂P(Y^∣X)
而这里的 P ( Y ^ ∣ X ) = ∑ h ∈ a l i g n ( Y ^ ) P ( h ∣ X ) P(\hat{Y}|X) = \sum_{h \in align(\hat{Y})}P(h|X) P(Y^∣X)=∑h∈align(Y^)P(h∣X)是一堆和 p 1 , 0 ( ϕ ) p_{1,0}(\phi) p1,0(ϕ), p 2 , 0 ( c ) p_{2,0}(c) p2,0(c), p 2 , 1 ( ϕ ) p_{2,1}(\phi) p2,1(ϕ), ⋯ \cdots ⋯这些相关的连乘和连加。故
∂ P ( Y ^ ∣ X ) ∂ θ = ∂ p 4 , 1 ( a ) ∂ θ P ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) + ⋯ \frac{\partial P(\hat{Y}|X)}{\partial \theta} = \frac{\partial p_{4,1}(a)}{\partial \theta} \frac{P(\hat{Y}|X)}{\partial p_{4,1}(a)}+\cdots ∂θ∂P(Y^∣X)=∂θ∂p4,1(a)∂p4,1(a)P(Y^∣X)+⋯
我们以 ∂ p 4 , 1 ( a ) ∂ θ P ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) \frac{\partial p_{4,1}(a)}{\partial \theta} \frac{P(\hat{Y}|X)}{\partial p_{4,1}(a)} ∂θ∂p4,1(a)∂p4,1(a)P(Y^∣X)为例,先来算一下 ∂ p 4 , 1 ( a ) ∂ θ \frac{\partial p_{4,1}(a)}{\partial \theta} ∂θ∂p4,1(a)。这个部分就和正常的RNN神经网络反向传播(BPTT)一致,这里不做说明。示意图如下所示。
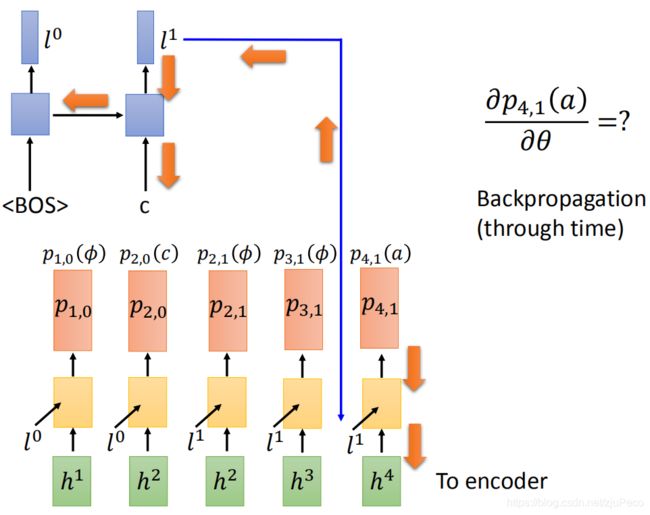
而在计算 P ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) \frac{P(\hat{Y}|X)}{\partial p_{4,1}(a)} ∂p4,1(a)P(Y^∣X)时,我们就可以把 P ( Y ^ ∣ X ) P(\hat{Y}|X) P(Y^∣X)拆分成
P ( Y ^ ∣ X ) = ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) + ∑ h w i t h o u t p 4 , 1 ( a ) P ( h ∣ X ) P(\hat{Y}|X) = \sum_{h\ with\ p_{4,1}(a)} P(h|X)+\sum_{h\ without\ p_{4,1}(a)} P(h|X) P(Y^∣X)=h with p4,1(a)∑P(h∣X)+h without p4,1(a)∑P(h∣X)
这里的第二项和 p 4 , 1 ( a ) p_{4,1}(a) p4,1(a)没有关系,故求偏导为0,可直接忽略,前一项可以写成
∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) = ∑ h w i t h p 4 , 1 ( a ) p 4 , 1 ( a ) × o t h e r s \sum_{h\ with\ p_{4,1}(a)} P(h|X) = \sum_{h\ with\ p_{4,1}(a)} p_{4,1}(a) \times others h with p4,1(a)∑P(h∣X)=h with p4,1(a)∑p4,1(a)×others
故
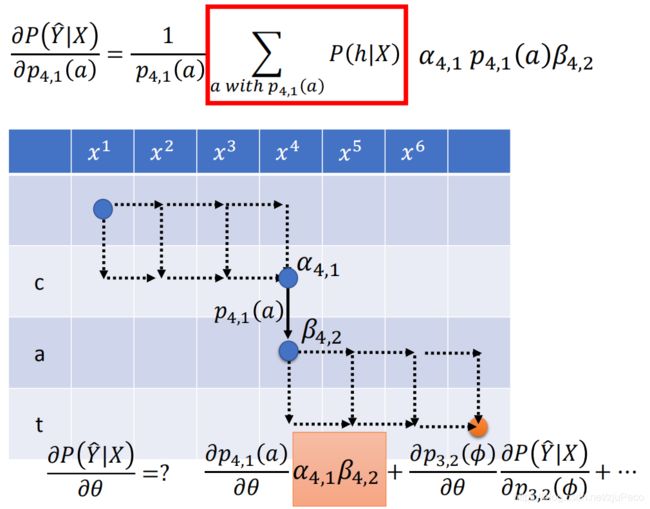
P ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) = ∑ h w i t h p 4 , 1 ( a ) o t h e r s = ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) p 4 , 1 ( a ) = 1 p 4 , 1 ( a ) ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) \frac{P(\hat{Y}|X)}{\partial p_{4,1}(a)} = \sum_{h\ with\ p_{4,1}(a)} others=\sum_{h\ with\ p_{4,1}(a)} \frac{P(h|X)}{p_{4,1}(a)}=\frac{1}{p_{4,1}(a)}\sum_{h\ with\ p_{4,1}(a)}P(h|X) ∂p4,1(a)P(Y^∣X)=h with p4,1(a)∑others=h with p4,1(a)∑p4,1(a)P(h∣X)=p4,1(a)1h with p4,1(a)∑P(h∣X)
那么问题来了,这个 ∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) \sum_{h\ with\ p_{4,1}(a)}P(h|X) ∑h with p4,1(a)P(h∣X)该怎么算呢?这里,我们就要引进HMM中的backward algorithm。这个和之前的forward algorithm很类似,我们定义一个参数 β i , j \beta_{i,j} βi,j表示从输入第 i i i个声音讯号,输出第 j j j个token的位置开始,一致走到终点的所有alignments的概率之和。
而这个 β i , j \beta_{i,j} βi,j也是和 α i , j \alpha_{i,j} αi,j一样,整个表格是可以事先填满的。

那么根据 α i , j \alpha_{i,j} αi,j和 β i , j \beta_{i,j} βi,j的定义,我们有
∑ h w i t h p 4 , 1 ( a ) P ( h ∣ X ) = α 4 , 1 p 4 , 1 ( a ) β 4 , 2 \sum_{h\ with\ p_{4,1}(a)}P(h|X) = \alpha_{4,1} p_{4,1}(a)\beta_{4,2} h with p4,1(a)∑P(h∣X)=α4,1p4,1(a)β4,2
那么就有
P ( Y ^ ∣ X ) ∂ p 4 , 1 ( a ) = α 4 , 1 β 4 , 2 \frac{P(\hat{Y}|X)}{\partial p_{4,1}(a)} = \alpha_{4,1} \beta_{4,2} ∂p4,1(a)P(Y^∣X)=α4,1β4,2
4 Inference
现在假设我们已经train好了一个模型,然后输出 X X X和 Y Y Y就可以计算出 P ( Y ∣ X ) P(Y|X) P(Y∣X)这个概率,那么我们要做的就是找到一个 Y ∗ Y^* Y∗使得 P ( Y ∗ ∣ X ) P(Y^*|X) P(Y∗∣X)最大。
Y ∗ = a r g m a x ⏟ Y P ( Y ∣ X ) Y^*=\underbrace{argmax}_{Y}P(Y|X) Y∗=Y argmaxP(Y∣X)
虽然有演算法可以做到这点,但还是太过复杂,实际情况下,我们不会那么去做。我们会去找一个近似的解。而这个求近似解的方法,就是取每一个 p i , j p_{i,j} pi,j中概率最大的那一个就可以了。这个也被称为greedy decoding。
如果希望更精确一些,也可以用Beam Search。greedy decoding可以说是beam search的一种特殊情况,就是beam=1的时候的情况。在遍历每个time step的时候,我会会一直保留一个大小为beam的候选集,候选集中是多个长度相等,但不同的字符串,每个字符串有一个score,也就是其概率大小。
比如我们有一个非常简单的输出矩阵为,其中#就是空白符 ϕ \phi ϕ

我们用beam search取找其最优组合的过程为
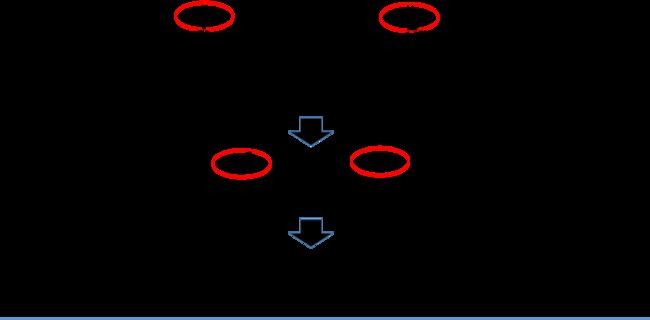
要注意的是,每次得到的新的字符串可能来自于不同的beam,要把他们的概率都加起来。beam越大,最终输出的结果就越准,但相应的计算成本也就更高。一般情况下,我们都是greedy search来做的,没必要用这个,仅作为了解。其实现可见[这里]。(https://github.com/githubharald/CTCDecoder/blob/master/ctc_decoder/beam_search.py)
5 小结
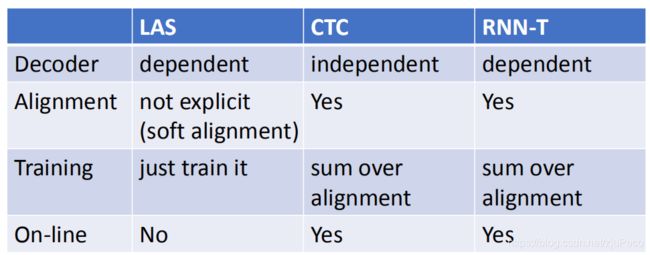
最后,我们来比较一下LAS,CTC以及RNN-T这三者的异同。在decoder这部分,LAS和RNN-T是依赖于之前的输出的,而CTC是不管的;CTC和RNN-T是需要对结果做alignment的,而LAS是输出什么就是什么的;LAS的training就是硬train一发,而CTC和RNN-T由于需要alignment,会复杂一些;LAS是无法做到句子还没念完就输出预测结果的,但是CTC和RNN-T是可以的。