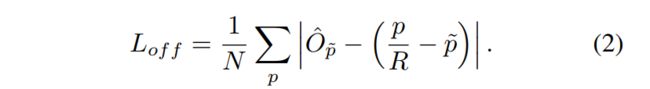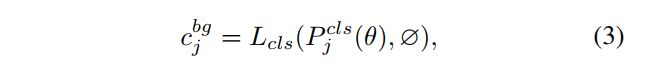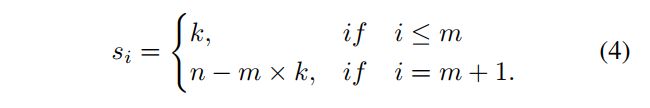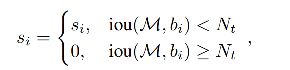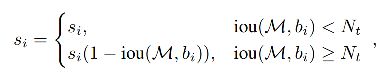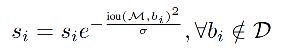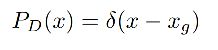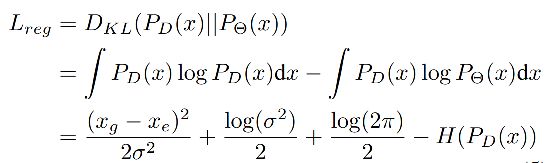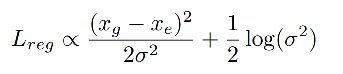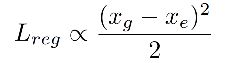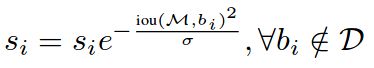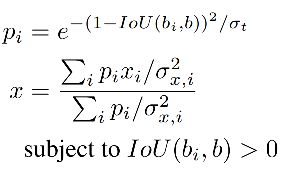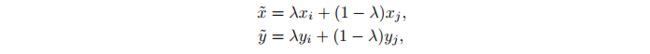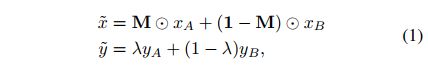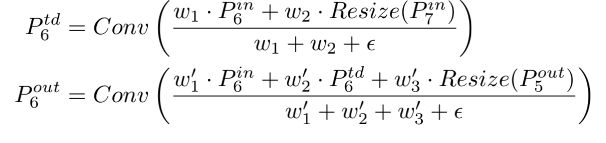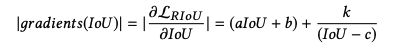【目标检测】56、目标检测超详细介绍 | Anchor-free/Anchor-based/Backbone/Neck/Label-Assignment/NMS/数据增强
文章目录
- 1、双阶段和单阶段目标检测器
-
- 1.1 双阶段目标检测器
-
- 1.1.1 R-CNN
- 1.1.2 SPP
- 1.1.3 Fast R-CNN
- 1.1.4 Faster R-CNN
- 1.2 单阶段目标检测器
-
- 1.2.1 YOLO 系列
-
- 1.2.1.1 YOLOv1
- 1.2.1.2 YOLOv2
- 1.2.1.3 YOLOv3
- 1.2.1.4 YOLOv4
- 1.2.1.5 Scaled-YOLOv4
- 1.2.1.6 YOLOv5
- 1.2.1.7 YOLOv6
- 1.2.1.8 YOLOv7
- 1.2.2 SSD
- 1.2.3 RetinaNet
- 1.2.4 CenterNet
- 1.2.5 FCOS
- 2、Label Assignment
-
- 2.1 RetinaNet
- 2.2 FCOS
- 2.3 ATSS
- 2.4 Free Anchor
- 2.5 AutoAssign
- 2.6 PAA
- 2.7 OTA
- 2.8 SimOTA
- 3、后处理之 NMS
-
- 3.1 NMS
- 3.2 Soft NMS
- 3.3 Softer NMS
- 3.4 IoU-Net:IoU-Guided NMS
- 3.5 FCOS:Centerness-NMS
- 3.6 GFLV1:Classification-IoU-NMS
- 3.7 GFLV2:DGQP-NMS
- 4、数据增强
-
- 4.1 Cutout
- 4.2 Random Erasing
- 4.3 Mixup
- 4.4 CutMix
- 4.5 Mosaic
- 4.6 Copy-paste
- 4.7 Grid-Mask
- 4.8 Fence-Mask
- 5、Neck
-
- 5.1 FPN
- 5.2 PAN
- 5.3 NAS-FPN
- 5.4 BiFPN
- 6、Backbone
-
- 6.1 GoogLeNet
- 6.2 ResNet
- 6.3 ResNeXt
- 6.4 DenseNet
- 6.5 CSPNet
- 6.6 RepVGG
- 6.7 MobileNet 系列
-
- 6.7.1 MobileNetV1
- 6.7.2 MobileNetV2
- 6.7.3 MobileNetV3
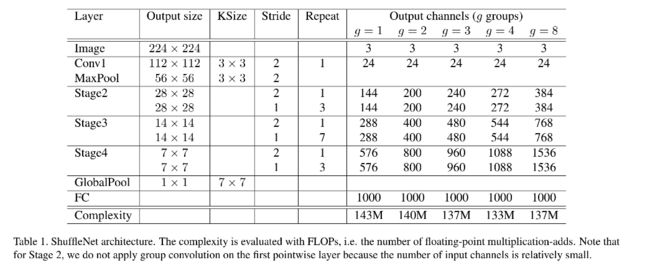
- 6.8 ShuffleNet 系列
-
- 6.8.1 ShuffleNetV1
- 6.8.2 ShuffleNetV2
- 6.9 VoVNet
- 7、Loss 函数
-
- 7.1 分类 loss 函数
-
- 7.1.1 CrossEntropy Loss
- 7.1.2 带权重的交叉熵Loss
- 7.1.3 Focal Loss
- 7.1.4 Varifocal loss
- 7.2 定位 loss 函数
-
- 7.2.1 L1 损失
- 7.2.2 L2 损失
- 7.2.3 Smooth L1 损失
- 7.2.4 IoU 损失
- 7.2.5 GIoU 损失
- 7.2.6 Distance-IoU 损失
- 7.2.7 Foal-EIoU 损失
- 7.2.8 R-IoU 损失
- 7.2.9 Alpha-IoU 损失
本博客还有多个超详细综述,感兴趣的朋友可以移步:
卷积神经网络:卷积神经网络超详细介绍
目标检测:目标检测超详细介绍
语义分割:语义分割超详细介绍
NMS:让你一文看懂且看全 NMS 及其变体
数据增强:一文看懂计算机视觉中的数据增强
损失函数:分类检测分割中的损失函数和评价指标
Transformer:A Survey of Visual Transformers
机器学习实战系列:决策树
YOLO 系列:v1、v2、v3、v4、scaled-v4、v5、v6、v7、yolof、yolox、yolos、yolop
目标检测在过去 20 年的发展很迅速,19 年之前的方法发展路线如下图所示,19 年之后的方法没有在图中,而且也没有合适的图来展现,但本文的内容也会涉及很多 19 年之后的方法。
其中比较重要的就是红字的那些方法,目标检测的发展和优化可以从下面几个方面来看:
- 从发展脉络上来看:主要分为单阶段和双阶段,单阶段胜于速度,双阶段胜于准确
- 从 backbone 的结构来看:有适合于云端 GPU 的大模型,也有适合边端 GPU 或 CPU 的小模型,也有使用重参数化来实现训练和测试结构的转化,使模型适合于不同的场合
- 从 proposal 生成的实现方法来看:可以划分为 anchor-based 和 anchor-free
- 从特征的层级结构来看:可以划分为使用多尺度特征和单尺度特征
- 从训练策略来看:有数据增强、多尺度训练、
- 从推理策略来看:多尺度测试、重参数化推理等
- 从后处理来看:有各种的 NMS 层出不穷(soft、softer、centerness、GFv1 和 GFv2 等等)
- 从 loss 函数来看:各种分类 loss(如 focal loss、GF loss、Varifocal loss 等)和回归 loss(如 IoU、GIoU、DIoU loss)
上述的分类方法只是大致的区分,很多目标检测方法是会重复出现在不同的类别中的。
1、双阶段和单阶段目标检测器
顾名思义,单阶段检测器是一次训练实现目标检测结果的输出,双阶段检测器是两次训练实现目标检测结果的输出。R-CNN 是 2014 年提出的一种开创性的双阶段目标检测器,与之前基于传统检测框架 segdmp 的方法相比,R-CNN 在 Pascal VOC 2010 上获得了 53.7% 的 mAP,比 segdmp 的 40.4% 高了 13.3% mAP,也拉开了基于深度学习的目标检测的序幕。
1.1 双阶段目标检测器
在基于深度学习的目标检测刚开始发展的阶段,以 R-CNN 为代表的方法火爆一时,其衍生出来的 Fast 和 Faster R-CNN 和其共同构成了 R-CNN 家族,也是双阶段目标检测器的代表。
![]()
1.1.1 R-CNN
详细介绍见 本文
论文:Rich feature hierarchies for accurate object detection and semantic segmentation
出处:CVPR 2014
主要贡献:开创了使用深度学习进行目标检测的任务,提出了 proposal 的概念,使用 proposal 生成 + proposal 特征提取(SVM 分类 + 回归)两阶段的过程,完成了目标检测
R-CNN 的训练流程可以分为三部分:
- proposal 生成:使用 selective search 的方法生成约 2k 候选框,然后 resize 成 227x227 大小(会导致物体形变)
- proposal 特征提取:对每个相同大小的候选区域都经过 CNN 进行特征提取,得到 4096-d 的特征向量
- proposal 分类和边界回归:使用 “一对多” 的 SVM 分类器进行分类,并学习边界回归,优化区域位置
R-CNN 的测试过程:
- 在测试集的每张图,先使用 SS 的方法选择约 2k 候选框,将候选框 resize 后送入 CNN 进行特征提取
- 对于每个类别,使用利用该类数据训练得到的 SVM,对每个提取的特征向量进行评分,得到类别
- 对所有判断为正例的框,使用 NMS 剔除掉一些框
R-CNN 的缺点:
- 每个候选区域都要 resize 到相同的大小,会导致目标的外观发生形变,降低模型的学习效果
- 对每个区域都要经过 CNN 造成了很多的重复计算,训练和测试都非常耗时
- 三个步骤(生成候选区域、特征提取、分类)都是独立的部分,不能端到端的训练,难以获得全局最优解
- 区域提议基于低层的视觉线索,难以在复杂的背景下产生高质量的提议
1.1.2 SPP
详细介绍见 本文
论文:Spatial pyramid pooling in deep convolutional networks for visual recognition
出处:ECCV 2014
主要贡献:使用空间金字塔池化的方法,免去了对输入图像的 reisize 过程,并且使用先提取特征,再抠出 proposal 对应区域特征的方法,一次完成特征提取,加速的训练过程。
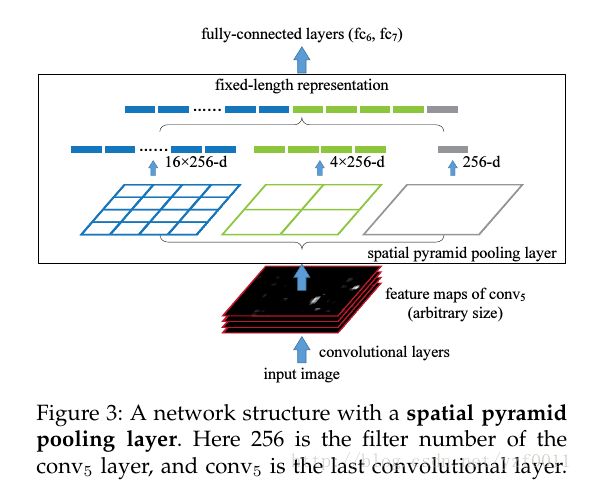
SPP 全称为 Spatial Pyramid Pooling(空间金字塔池化),R-CNN 的 CNN 结构,由于后面的全连接层需要接收固定尺度的向量(如 4096-d),所以需要 CNN 输入固定大小的图像。一般会使用 crop 和 warp 来将图像进行大小的统一,但这样会破坏纵横比,影响目标的外观,于是何凯明提出了 SPP,连接在全连接层的前一层,使得 CNN 网络可以使用任意大小的图像。
SPP 工作过程:
- 利用 SS 方法获得区域提议,通过 Stride 区域映射的方法,在卷积层的后面加入位置信息,便于在卷积特征图中找到每个区域的位置。
- 对整张图进行卷积特征提取,解决了卷积层的重复计算的问题
- 空间金字塔池化,也就是替换最后一个池化层为 SPP pooling layer
- SVM分类
SPP 的结构的特点:
- 输入特征图大小任意:将金字塔思想加入 CNN 中,使用多种不同尺度的 pooling,pooling 会根据输入来调整大小(如设定每个 pooling 的输出分别为 4x4=16、2x2=4、1x1=1 这三个维度,则自适应池化会根据输出特征图的大小来自动进行 pooling,让输出的向量维度相同,所以输入特征图可以是任意维度)
- 输出特征向量大小固定:将多个 pooling 的结果 concat 起来,得到相同尺度的特征向量
- 只需要进行一次 CNN 特征提取:先提取特征,将候选框的特征直接输入 SPP 后面的层,节省了大量的计算时间,比 R-CNN 有 100 倍的提速
SPP 为什么金字塔池化的结构的好处:
- 多个不同尺度的 pooling 窗口会提高准确率
- 输入图像大小任意,就避免了对输入目标的 resize,不会导致目标外观过度改变
SPP 的缺点:
- 提取候选框 | 计算CNN特征 | SVM分类 | 回归训练过程都是各自独立的,大量中间结果需要转存,无法整体训练参数
- 无法同时微调卷积层和全连接层,在很大程度上限制了CNN的效果
- 候选区域仍然使用SS方法,很耗时
1.1.3 Fast R-CNN
详细介绍见 本文
论文:Fast R-CNN
出处:ICCV 2015
贡献:将 SPP 中的一次性特征提取和 R-CNN 结合起来,并在 SPP 的基础上,提出了 RoI pooling,只使用单尺度的 max pooling 来进行特征提取,获得固定长度的特征向量。并且抛弃了 SVM 使用了 softmax 进行分类,将 R-CNN 的结构改成了并行结构,能够同时进行分类和回归。
有了 R-CNN 和 SPP 的积累,Fast R-CNN 就融合了前面两者的优势,实现了快速的 R-CNN。
![]()
Fast RCNN 的工作过程:
- 首先,使用 Selective Search 的方法生成一系列候选区域
- 然后,对整幅图像进行卷积特征提取,将最后一层的池化层替换成 RoI pooling 层,输出固定长度的特征向量
- 最后,将 RoI pooling 的输出向量输入全连接层,用于多任务学习并计算多任务损失,输出两个分支:softmax 分类分支(使用 log loss 计算 k+1 个类别的损失函数);regression 回归分支(使用 smooth L1 loss)计算每个框的 bbox 坐标
什么是 RoI pooling 中的 RoI:
输入图片在经过卷积网络得到 feature maps 后,利用 SS 或者 RPN 算法来得到多个目标候选框,这些以输入图片为参考坐标的候选框在 feature maps 上的映射区域,即为目标检测中所说的 RoI,也就是从原图的某个位置映射到特征图上的某个位置,特征图上的该区域就是 RoI。
RoI pooling 的过程:从任意大小特征图中获得固定大小的特征向量
- 根据输入图像,将 RoI 从原图映射到 feature map 对应位置
- 将映射后的区域根据输出向量的大小划分为小块,小块数量与输出的维度相同,小块内的像素个数是整数,如果边长不能被小块长整除,则最后一个小块内的像素个数和前面的不同,或少或多,但不会取像素中间的值,每个小块内的像素个数总数整数
- 对每个小块内进行 max pooling 操作
RoI pooling 的问题:RoI pooling 会有两次量化问题,这两次量化的结果都使得候选框的位置出现了偏差
- 第一次:候选框从原图坐标映射到的 feature map 坐标时,位置坐标可能存在浮点数,此时进行取整操作从而出现第一次量化
- 第二次:在 RoI Pooling 求取每个小网格的位置时也同样存在浮点数取整的情况
RoI Align:
为了解决 RoI Pooling 两次量化问题,RoI Align 不再采用取整量化操作,而是保留了浮点数的运算,并使用双线性插值的方式来求取像素值。具体的过程步骤如下,假设需要输出 2x2 大小的特征图
- 首先将 RoI 区域切分成 2x2 的单元格,不取整不量化,保留小数
- 如果要切分的小块总数是 4,则将每个单元格子均分成四个小方格,以每个小方格的中心作为采样点
- 对采样点像素进行双线性插值,得到该像素点的值
- 对每个单元格内的四个采样点进行 max pooling,得到最终的 ROI Align 结果
Fast R-CNN 的问题:
- 仍然使用 Selective Search 来生成候选区域,很耗时
1.1.4 Faster R-CNN
详细介绍见 本文
论文:Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks
贡献:提出了 RPN 来实现 proposal 生成,每张图大概 300 个提议框,使得目标检测可以端到端的完成
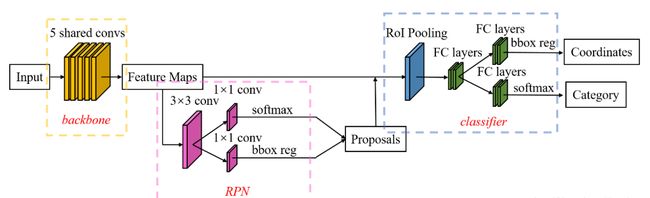
Faster R-CNN 的工作过程:
- 首先,将整幅图像输入 CNN 网络,得到卷积特征图
- 然后,将卷积特征图输入 RPN 网络,生成 anchor 的类别(前景/背景)和位置
- 接着,将 anchor 的位置从对应的初始卷积特征图上抽取出来,送入 RoI pooling
- 最后,将 RoI pooling 特征送入全连接层,后面接上分类和回归的两个 head,得到最终的结果
Faster R-CNN 如何训练:四步交替优化法
- 训练 RPN:使用 ImageNet 预训练模型对 RPN 进行进行初始化,训练 RPN 网络
- 训练 Fast R-CNN:使用 ImageNet 预训练模型初始化检测网络,并固定 RPN 网络参数,使用 RPN 得到的 proposal,训练 Fast R-CNN 的检测网络(也就是除过 RPN 外的所有需要训练的层都算作检测网络的部分)
- 调优 RPN:使用检测网络训练好的共享卷积(即主分支那些参数),固定共享卷积,继续修正 RPN 网络
- 调优 Fast R-CNN:保持共享卷积层的固定,使用调优后的 RPN 网络,对 Fast R-CNN 的一些层进行微调
RPN 实际上也是一个小的卷积网络,3x3 卷积后面跟两个并行 1x1 卷积,且 RPN 可以与检测网络共享整幅图像的卷积特征,从而产生几乎无代价的区域推荐。RPN loss = cls loss + reg loss。
RPN 的结构如下,所以 RPN 的参数量很少
- 3x3 卷积,因为 RPN 的输入是经过 CNN 提取后的特征,更适用于分类任务,这个 3x3 的卷积或许可以提取一些更适合检测任务的特征
- 两个并行 1x1 的 head,分别进行二分类和回归
![]()
RPN 的工作过程:
- 首先,在卷积特征图上的每个点上,生成 k 个 anchor(这里使用的 k=9, 3 种面积,128x128、256x256、512x512,3 种宽高比,1:1, 1:2, 2:1,假设特征图大小为 40x90,则共有 40x90x9 个初始 anchor)
- 然后,对每个 anchor 使用 3x3 的卷积进行特征提取,之后输入分类头和回归头,分类头是对 k 个 anchor 判断其属于前景还是背景,也就是一个 2 分类网络,输出为 2k 个得分,回归头是给 k 个 anchor 回归位置偏移,输出为 4k 个偏移坐标
- 接着,对所有的 anchor,判断其为前景还是背景后,对前景 anchor 进行一次坐标修正(smooth L1 loss 进行训练),对于第一步生成的 k 个 anchor,得到预测的正负结果后,和这些 anchor 的真值进行对比,求 loss,而真值是使用 anchor 和 gt 的 IoU 来判定的。
- 最后,得到了这些 anchor 后,按照得分排序,保留特定数量的 anchor,输入到 RoI pooling 中去
anchor 训练时 label 的正负如何给定:
- 正样本:如果 anchor 和 gt 的 IoU > 0.7,则标记为正样本,如果最大的也小于 0.7 ,则标记最大的 IoU 对应的 anchor 为正
- 负样本:如果 anchor 和 gt 的 IoU < 0.3,则标记为负样本
- 非正非负,不参与训练:如果 0.3
注意:
训练时,会将与边界有交叉的 anchors 删除,否则会难以收敛。测试时,仅仅将与边界交叉的anchors 切到边界即可。
1.2 单阶段目标检测器
经过上面的介绍,我们已经知道了双阶段目标检测器主要是分为 region proposal 和 detection 两个阶段,但双阶段目标检测器的很大的缺点就是训练时间过长且推理速度也慢,故此就出现了能够一次性完成训练的单阶段目标检测器,将 region proposal 也放入了检测模型训练过程中。
1.2.1 YOLO 系列
YOLO 系列中既有 anchor-free 的结构,也有 anchor-based 的结构
1.2.1.1 YOLOv1
详细介绍见 本文
论文:You Only Look Once: Unified, Real-Time Object Detection
代码:https://pjreddie.com/darknet/yolo/
作者:Joseph Redmon
时间:2016.05
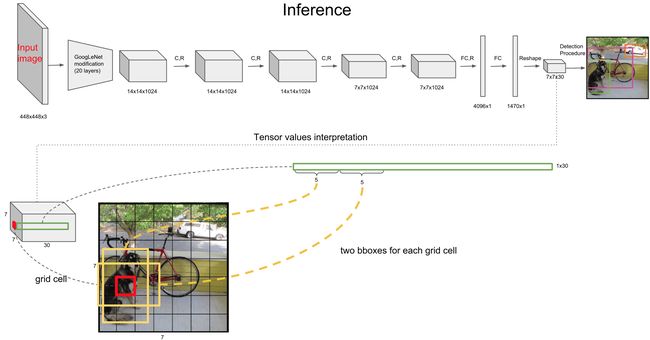
YOLOv1 提出将目标检测任务定义为单个回归问题,直接从输入图像上得到框的位置和类别。将整个图像空间分割为固定数量的网格单元(例如,使用7×7网格)。每个 cell 都是可以检测一个或多个物体的 proposal。
在最初的实现中,认为每个 cell 包含两个对象的中心。对每个 cell 进行预测:预测该位置是否有对象、边界框坐标和大小(宽度和高度)以及对象的类别。整个框架是一个单一的网络,它省略了建议生成步骤,可以端到端优化。
YOLOv1 结构介绍:
- 输入:将图像分为 S × S S\times S S×S 的网格(7x7),如果目标的中心点落入了对应网格,则由该网格负责预测该目标
- 每个网格预测 2 个 bbox 和每个 bbox 中包含目标的概率,定义 confidence 为 P r ( o b j e c t ) × I o U p r e d t r u t h Pr(object) \times IoU_{pred}^{truth} Pr(object)×IoUpredtruth
- 如果某个网格没有目标落入,则对应 confidence 为 0,否则期望 confidence score = IoU
- 每个 bbox 的预测包含五个参数: ( x , y , w , h , c o n f i d e n c e ) (x, y, w, h, confidence) (x,y,w,h,confidence), ( x , y ) (x, y) (x,y) 为框的中心点和网格边界的距离(相对当前网格的偏移值), ( w , h ) (w, h) (w,h) 是宽高和全图比(相当于归一化了),confidence代表了所预测的box中含有 object 的置信度和这个 box 预测的有多准两重信息。
- 每个网格也会预测类别 P r ( C l a s s i ∣ O b j e c t ) Pr(Class_i|Object) Pr(Classi∣Object),也就是每个框会预测其对应类别。
- 测试时,对每个框预测的类别如下,该类别包含了这个 bbox 中该类别的概率和位置匹配的准确性: P r ( c l a s s i ∣ o b j e c t ) ∗ P r ( O b j e c t ) ∗ I o U p r e d t r u t h = P r ( C l a s s i ) ∗ I o U p r e d t r u t h Pr(class_i|object)*Pr(Object)*IoU_{pred}^{truth}=Pr(Class_i)*IoU_{pred}^{truth} Pr(classi∣object)∗Pr(Object)∗IoUpredtruth=Pr(Classi)∗IoUpredtruth
- 在 PASCAL VOC 测试时,作者使用 S=7,B=2,C=20,最终得到 7x7x30 的向量
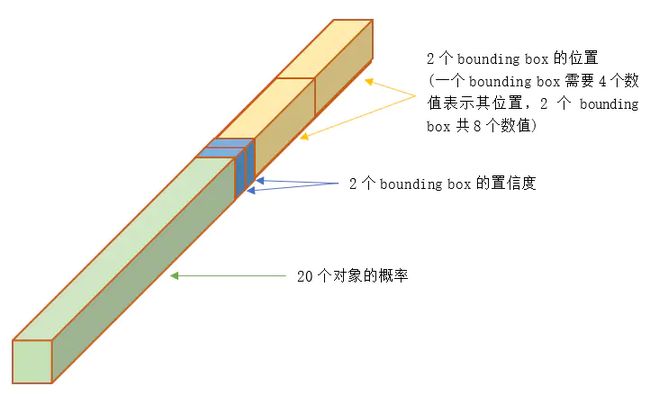
为什么每个网格输出 30 维向量:
30 维向量 = 20 个目标的类别概率(VOC 类别) + 2 个 bounding box x4 个坐标 + 2 个 bounding box 包含目标的置信度 confidence(前、背景)
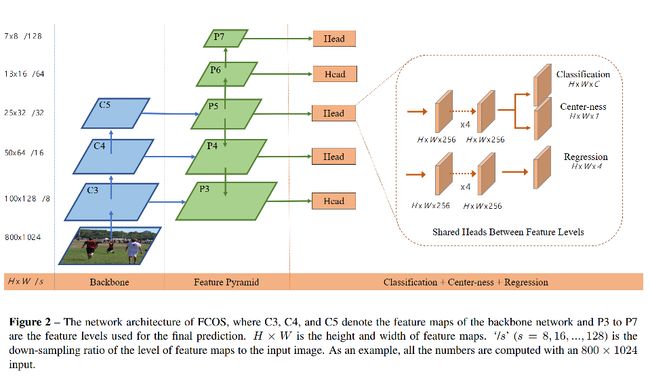
网络结构:如下图 3
- 标准结构:24 conv layers + 2 fully connected layers
- Fast 结构:9 conv layers + 2 fully connected layers
- 输出:7x7x30 tensor
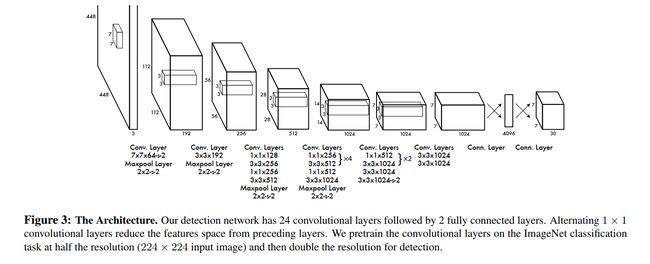
每个网格被认为只属于一个目标,所以虽然会预测两个框,但这个两个框都属于一个类别,只是两个框位置而已,后面还会剔除掉得分低的框,这个得分是每个框包含目标的概率,而不是用那 20 个类别的向量来判断的。
训练:
- 输入 448x448 的图像,输出 7x7x30 的向量
- 输出每个网格中的每个框的 ( x , y , w , h , c o n f i d e n c e ) (x, y, w, h, confidence) (x,y,w,h,confidence)
- 虽然每个网格中可能预测多个 bbox,在训练阶段,只期望对每个目标预测一个框,故此处指保留和 gt 的 IoU 最大的框。
推理:
- 在每个图像中预测 98 个bbox(49 个网格,每个网格预测两个框,保留 IoU 最大的那个)
- 每个网格会预测两个 bbox,通过 NMS 后,会保留一个 bbox
Loss 函数:
- 1 i o b j 1_i^{obj} 1iobj 是第 i i i 个网格中存在目标
- 1 i j o b j 1_{ij}^{obj} 1ijobj 是第 i i i 个网格中的第 j j j 个 bbox 存在目标
- 可以看出该 Loss 函数只对出现在该网格中的目标进行分类约束,也只对出现在该网格中的 IoU 最大的框进行约束。
如何进行 NMS:
因为我们对一个网格要预测两个bbox,所以最后我们能得到个 7x7x2=98 个bbox。
首先,将这 98 个 bbox 中置信度低的框去掉,然后再根据置信度对剩下的 bbox 排序,使用 NMS 算法,把重复度高的框的置信度设为 0。
对于留下的框,再根据分类概率得到它们的类别,这里注意得到的框的大小都是相对于原图大小的,都是 0~1 之间的值,所以输出的时候还需要还原,才能得到真实的 bbox 的尺寸大小。
YOLO 也面临着一些挑战:
- 它在给定位置只能检测到两个对象,这使得很难检测到小对象和拥挤的对象[40]
- 只有最后一个特征图用于预测,不适合多尺度、多纵横比的目标预测
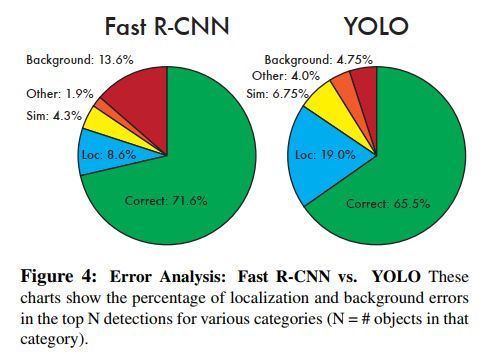
- YOLO v1 定位错误较多,定位的错误高于其他所有错误的总和
- Fast RCNN 定位错误的很少,但有很多背景误识别,13.6% 的检测结果是假正,即不包含任何目标,约是 YOLO v1 背景误识别的 3 倍。
优势如下:
- YOLOv1 很快!由于不需要复杂的 pipeline,在 Titan X GPU 上能达到 45fps,能够实时处理视频流,且准确率是当时实时系统的 2 倍。
- YOLOv1 在推理的时候在全图上进行,在训练和测试时都将全图看做一个整体,没有 RPN 等操作,比 Fast R-CNN 对背景的误检少了一半(Fast RCNN 由于无法看到全局的信息,所有很多背景的误检)。
- YOLOv1 能够学习到目标更泛化的特征。
- YOLOv1 虽然比当时 SOTA 的方法效果差些,但速度很快。
YOLO v1 的不足:
- YOLO v1 在每个网格中预测两个框,并且属于同一个类别,这种空间约束限制了对距离近的目标的预测,会导致漏检,如多个小目标共现的区域
- YOLO v1 模型是从训练数据中学习到的目标纵横比,所以难以泛化到少见的纵横比目标上,导致边界不准。
- YOLO v1 的 loss 函数将大目标和小目标同等对待,大目标的小错误是可以容忍的,但小目标的小错误对 IoU 影响较大,会导致对小目标定位不准
- 使用全连接层,参数量巨大,而且也因此在检测时,YOLO 训练模型只支持与训练图像相同的输入分辨率。
- 一个网格只能预测一个物体。
- anchor-free的方法没有anchor-based的准确。
从图 4 可以看出:
- YOLO v1 定位错误较多,定位的错误高于其他所有错误的总和
- Fast RCNN 定位错误的很少,但有很多背景误识别,13.6% 的检测结果是假正,即不包含任何目标,约是 YOLO v1 背景误识别的 3 倍。
1.2.1.2 YOLOv2
详细介绍见 本文
论文:Yolo9000: Better, faster, stronger
代码:https://github.com/pjreddie/darknet
出处:CVPR2017
作者:Joseph Redmon
时间:2016.12
YOLOv1 有很多不足,其中最主要的两点在于:
- 定位不准
- Recall 低
所以 YOLOv2 也主要在提高这两个问题上下功夫。YOLOv2 没有提高模型大小,速度更快了,主要从以下方面来让网络效果更好
即:更好、更快、更强三方面来进行优化
1、更好
-
1、Batch Normalization:在 YOLOv1 的所有卷积层后面加 BN,提升了 2mAP
-
2、High Resolution Classifier:YOLOv1 使用 224x224 大小预训练,YOLOv2 提升到了 448x448 大小,能帮助网络在大分辨率输入上更好提取特征
-
3、回归使用了 anchor 来预测框。输入图像大小 416x416(为了保证奇数大小特征图),下采样 32 倍,得到 13x13 大小特征图,每张图上能预测的目标从 98 变成了 1k 多,也提出了objectness,预测每个 anchor 和 gt 的 IoU,和该 anchor 是目标的概率无 anchor 时 mAP=69.5,recall=81%,有 anchor 后,mAP=69.2,recall=88%。提升了 recall 后,表示模型有了更大的提升空间。
-
4、使用了聚类的方法来选择 anchor 的尺度,避免了手动选择需要调参,在训练集上使用了 k-means 来自动选择最优的值。由于欧氏距离对尺寸很敏感,所以作者使用 d ( b o x , c e n t r o i d ) = 1 − I o U ( b o x , c e n t r o i d ) d(box, centroid) = 1-IoU(box, centroid) d(box,centroid)=1−IoU(box,centroid) 的方式来度量距离。 5 种形心的聚类方法得到的框的效果和 9 种 anchor box 效果类似。使用 9 种形心的聚类方法能够得到更高的 IoU。
-
5、多尺度预测,YOLOv2 在 13x13 的特征图上预测,但得益于大特征图的预训练,这样的大小也也足够大目标的预测了。但同时也在 26x26 大小的特征图上也引出了分支,得到了 1% 的性能提升。
-
6、Multi-scale Training
- YOLOv1 中使用大小为 448x448 的输入,YOLOv2 中由于要添加 anchor,所以改成了 416x416,但为了对不同大小的目标更加鲁棒,所以 YOLOv2 使用了多尺度训练。
- 多尺度训练的模式:在每 10 个 epoch 随机选择训练的尺度,由于最后下采样 32 倍,所以作者选择了 32 的倍数:{320, 352, …, 608},最小的为 320, 最大的为 608。
- 这种机制迫使网络学习跨各种输入维度进行良好的预测。这意味着同一个网络可以在不同的分辨率下预测检测结果。网络在较小的尺寸下运行速度更快,因此 YOLOv2 可以轻松地在速度和精度之间进行权衡。
- 在低分辨率时,YOLOv2 是一种耗费小而相当精确的检测器,288x288 大小时,可以达到 90 FPS,且 mAP 和 Fast RCNN 类似。
- 在高分辨率时,YOLOv2 在 VOC2007 上达到了 SOTA的 78.6 mAP,且接近实时速度。
2、更快
-
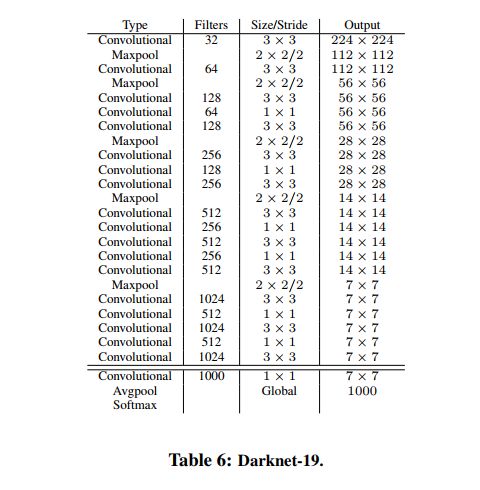
YOLOv2 中提出了一个新的分类模型,Darknet-19,共 19 层卷积层,5 层 maxpooling,结构见表 6
-
Training for classification
训练 ImageNet-1000 共 160 epochs,使用 SGD,训练时使用标准数据增强(crop、rotation、hue、saturation、exposure shifts等)。
先使用 224x224 训练,然后使用 448x448 微调,微调共使用 10 个epochs。
-
Training for detection
检测网络,作者移除了最后一个卷积层,使用 3 个 3x3 conv (1024 个通道)+ 1 个 1x1 conv(通道和类别相关,对于 VOC,5 bbox * 5 coordinates + 5 bbox * 20 cls = 125)。
3、更强
- 将 coco 和 ImageNet 联合训练,让网络从分类数据中学到更多的类别,从检测数据中学到更多的位置信息
1.2.1.3 YOLOv3
详细介绍见 本文
论文: YOLOv3: An Incremental Improvement
代码:https://github.com/pjreddie/darknet
作者:Joseph Redmon
时间:2018.08
由于 YOLO 系列对小目标的检测效果一直不太好,所以 YOLOv3 主要是网络结构的改进,使其更适合小目标检测;
YOLOv3 提出了 objectness score,使用 logistic 回归的方法来对每个框预测 objectness score:
- 1:当一个先验框和 gt 的重合率大于其他先验框时,objectness score = 1
- -1:当一个先验框的 IoU 不是最大,但大于阈值时(0.5),则 objectness score = -1,不参与训练
YOLOv3 在 3 个尺度上进行框的预测,最后输出三个信息:bbox、objectness、class
在 COCO 数据集中,就会在每个尺度上输出:
- N × B × [ 3 ∗ ( 4 + 1 + 80 ) ] N\times B \times [3*(4+1+80)] N×B×[3∗(4+1+80)] 偏移信息
- 1 个 objectness
- 80 个类别预测
预测要点:
- 使用 k-means 距离的方法来确定先验 bbox,9 个形心和 3 个尺度,然后使用尺度来将这些簇分开
- COCO 上的 9 个簇分别为:(10x13), (16x30),(33x23), (30x61), (62x45), (59x119), (116x90), (156x198), (373x326)。
在 YOLOv2 中使用的是 Darknet-19,YOLOv3 使用 Darknet-53。
![]()
YOLOv3 的 APs 指标表现很好,但在大中型目标上效果较差,需要继续研究
1.2.1.4 YOLOv4
详细介绍见 本文
论文:YOLOv4: Optimal speed and accuracy of object detection
代码:https://github.com/AlexeyAB/darknet
作者:AlexeyAB
时间:2020.08
致力于设计一个快速的检测器,称为 YOLOv4,贡献点如下:
- 设计了一个又快又好的检测器
- 验证了很多 Bag of Freebies 和 Bag of Specials 方法的效果
- 证明了现有的 SOTA 的方法可以更有效并且在单个 GPU 上训练
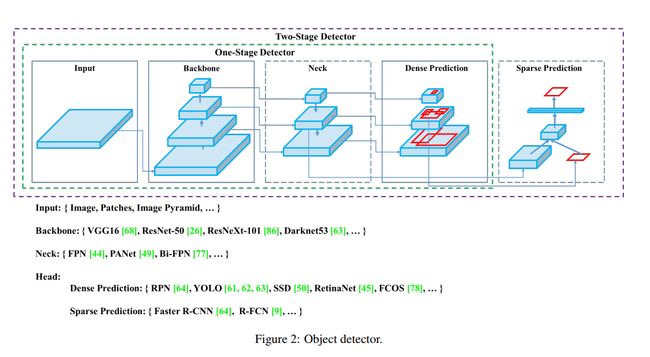
YOLOv4 将目标检测器分为了 4 个部分:
- Input:Image、Patches、Image Pyramid
- Backbone:VGG-16、ResNet、EfficientNet 等
- Neck:
- Additional blocks:SPP、ASPP、RFB、SAM 等
- Path-aggregation blocks:FPN、PAN、NAS-FPN、ASFF 等
- Heads:
- Dense Prediction(one-stage):
- RPN、SSD、YOLO、RetinaNet(anchor based)
- CornerNet、CenterNet、FCOS(anchor free)
- Sparse Prediction(two-stage):
- Faster RCNN、R-FCN、Mask RCNN(anchor based)
- RepPoints(anchor free)
- Dense Prediction(one-stage):
Bag of Freebies:指的是那些不增加模型复杂度,也不增加推理的计算量的训练方法技巧,来提高模型的准确度
Bag-of-Specials:指的是那些增加少许模型复杂度或计算量的训练技巧,但可以显著提高模型的准确度
BoF指的是:
- 数据增强:图像几何变换(随机缩放,裁剪,旋转),Cutmix,Mosaic等
- 网络正则化:Dropout、Dropblock等
- 损失函数的设计:边界框回归的损失函数的改进 CIOU
BoS指的是:
- 增大模型感受野:SPP、ASPP等
- 引入注意力机制:SE、SAM
- 特征集成:PAN,BiFPN
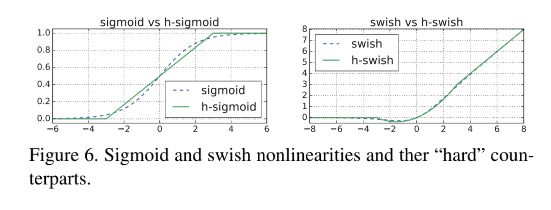
- 激活函数改进:Swish、Mish
- 后处理方法改进:soft NMS、DIoU NMS
YOLOv4 由以下三个部分组成,使用了很多 BoF 和 BoS:
- Backbone:CSPDarknet53
- Neck:SPP, PAN
- Head:YOLOv3
使用的策略:
-
Backbone:
- BoF: CutMix and Mosaic data augmentation, DropBlock regularization, Class label smoothing
- BoS: Mish activation, Cross-stage partial connections (CSP), Multiinput weighted residual connections (MiWRC)
-
detector:
- BoF: CIoU-loss, CmBN, DropBlock regularization, Mosaic data augmentation, Self-Adversarial Training, Eliminate grid sensitivity, Using multiple anchors for a single ground truth, Cosine annealing scheduler [52], Optimal hyperparameters, Random training shapes
- BoS: Mish activation, SPP-block, SAM-block, PAN path-aggregation block, DIoU-NMS
1.2.1.5 Scaled-YOLOv4
详细介绍见 本文
论文:Scaled-YOLOv4: Scaling Cross Stage Partial Network
代码:https://github.com/WongKinYiu/ScaledYOLOv4
作者:Chien-Yao Wang、Alexey AB
出处:CVPR2021
时间:2021.02
作者将 YOLOv4 经过尺度缩放,分别适用于:general GPU、low-end GPU、high-end GPU
YOLOv4 是为在 general GPU 上运行的实时目标检测网络,作者又重新设计了一下,得到更好的 speed/accuracy trade-off 网络 YOLOv4-CSP
Backbone:
CSPDarknet53 的设计, cross-stage 的下采样卷积的计算是没有包含在残差块中的,故可以推理出 CSPDarknet 的计算量为 w h b 2 ( 9 / 4 + 3 / 4 + 5 k / 2 ) whb^2(9/4+3/4+5k/2) whb2(9/4+3/4+5k/2),所以 CSPDarknet stage 在 k>1 的时候的计算量是优于 Darknet 的,CSPDarknet53 的每个 stage 的残差层分别为 1-2-8-8-4,为了得到更好的 speed/accuracy trade-off,将 CSP 的第一个 stage 转换成原始的 Darknet 残差层。
Neck:
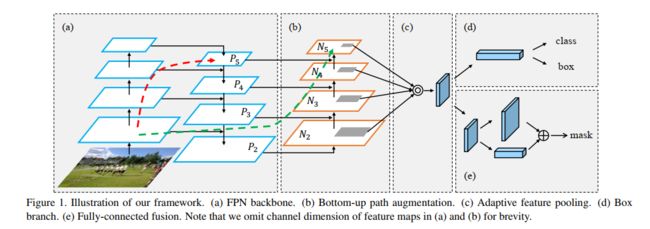
为了进一步降低计算量,也把 YOLOv4 中的 PAN 进一步 CSP-ize,PAN 结构的计算过程如图 2a 所示,它主要是整合来自不同特征金字塔的特征,然后经过两组反向 Darknet 残差层(没有 shortcut 连接),CSP-ization 之后的计算过程如图 2b 所示,降低了 40% 的计算量。
SPP:
SPP 模块也被嵌入 CSPPAN 的第一个 group 的中间位置
1.2.1.6 YOLOv5
详细介绍见 本文
论文:暂无
代码:https://github.com/ultralytics/yolov5
官方介绍:https://docs.ultralytics.com/
出处:ultralytics 公司
时间:2020.05
YOLOv5 是基于 YOLOv3 改进而来,体积小,YOLOv5s 的权重文件为27MB。
YOLOv4(Darknet架构)的权重文件为 244MB。YOLOv5 比 YOLOv4 小近 90%。这意味着YOLOv5 可以更轻松地部署到嵌入式设备。
此外,因为 YOLOv5 是在 PyTorch 中实现的,所以它受益于已建立的 PyTorch 生态系统
YOLOv5 还可以轻松地编译为 ONNX 和 CoreML,因此这也使得部署到移动设备的过程更加简单。
1.2.1.7 YOLOv6
详细介绍见 本文
论文:YOLOv6: A Single-Stage Object Detection Framework for Industrial
Applications
代码:https://github.com/meituan/YOLOv6
官方博文:https://blog.csdn.net/MeituanTech/article/details/125437630
作者:美团
时间:2022.09
YOLO 系列算法回顾:
- YOLOv1-v3,也是最初的 one-stage 检测器 YOLO 系列的开创者 Joseph Redmon 提出的,为后面的改进方法打了很好的基石
- YOLOv4 将检测框架结构划分为 3 个部分:backbone、neck、head,然后使用了很多策略来设计了一个适合在单 GPU 上训练的网络结构
- YOLOv5、YOLOX、PPYOLO、YOLOv7 都是为部署做了相关的工作,通过模型缩放的形式来适应于不同的场景
YOLOv6 主要做的工作如下:
- 设计了对硬件友好的 backbone 和 neck:设计了更高效的 Backbone 和 Neck :基于 RepVGG style[4] 设计了可重参数化、更高效的骨干网络 EfficientRep Backbone 和 Rep-PAN Neck。
- 有效的进行了 head 解耦:在维持精度的同时,进一步降低了一般解耦头带来的额外延时开销
- 在训练策略上,采用Anchor-free 无锚范式,同时辅以 TAL(YOLOv6 第一版使用的 SimOTA[2] )标签分配策略以及 SIoU[9] 边界框回归损失来进一步提高检测精度。
YOLOv6 的改进集中在如下部分:
- Network design
- Backbone:RepVGG 很适合小网络,但很难扩展到大网络(参数爆炸),所以使用 RepBlock 作为小网络的基础 block,使用 CSPStackRep block 作为大网络的 block。
- Neck:类似 YOLOv4 和 YOLOv5,使用 PAN 的结构,对大小网络都使用 Rep-PAN
- Head:对 head 进行了解耦,使用 Efficient Decoupled Head
- Label assignment:作者对很多方法都做了实验,最后选择了 TAL
- Loss function:VariFocal 为分类 loss,SIoU/GIoU 为回归 loss
- Data augmentation:Mosaic 和 Mixup
- Industry-handy improvements:作者引入了 self-distillation 和 更多的 epochs 来提高性能。self-distillation 是每个学生网络的分类和回归都被教师网络监督。
- Quantization and deployment:为了解决量化后的重参数化模型的性能下降问题,作者使用 RepOptimizer 的方法来得到 PTQ-friendly weights。
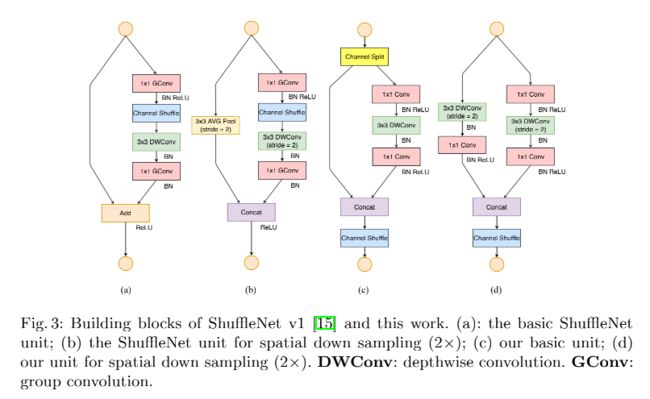
① Backbone:EfficientRep
- 小模型:
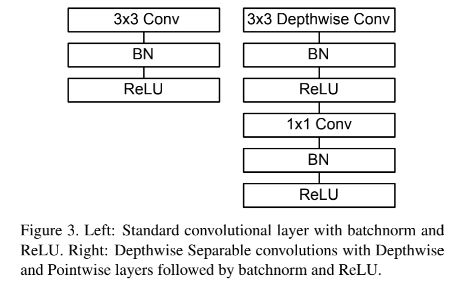
- 在训练中使用 Rep block,如图 3a
- 在推理时使用 RepConv,3x3 卷积 + ReLU 堆积而成的结构,如图 3b
- 大模型:
- 使用 CSPStackRep block 来得到中/大模型,如图 3c,3 个 1x1 conv + 2 个 RepVGG (训练) / RepConv (测试) + 1 个残差通道
② Neck:Rep-PAN
Neck 延续了 YOLOv4 及 YOLOv5 的架构——PAN,同样为了降低在硬件上的延时,在Neck上的特征融合结构中也引入了Rep结构,形成了 Rep-PAN
③ Head:Efficient decoupled head
④ Anchor-free
YOLOv6 中使用 anchor-point-based 大方式,也就是 box regression 分支是预测 anchor point 到 bbox 的四个边的距离。
⑤ Label Assignment:TAL
SimOTA:
SimOTA 是 OTA 的简化版本,将标签分配问题构造成了一个最优传输问题,通过找到最优传输方式,来得到每个 anchor 和 gt 的匹配结果。YOLOv6 的早期版本其实是使用的 SimOTA 的,那个时候论文还没有放出来,只有 github 代码。但由于 SimOTA 会拉慢训练速度,容易导致训练不稳定,所以又寻找了代替的方法。
Task Alignment Learning:
TAL 是在 TOOD 中被提出的,其中设计了一个【分类得分和定位框质量的统一度量标准】,使用该度量结果代替 IoU 来帮助分配标签,有助于解决任务不对齐的问题,且更稳定,效果更好。
⑥ loss:VariFocal Loss (VFL),SIoU,其他使用 GIoU
⑦ 训练更多的 epochs
⑧ Self-distillation
为了提高模型效果,但不引入额外开销,作者使用了 KL 散度作为衡量学生网络和教师网络分布的指标。
为什么叫做 self-distillation 呢?就是因为这里 学生网络=教师网络。
KL 散度整你用来衡量数据分布的差异,所以只能适用于分类结果,作者又参照了 DFL loss,也将其用于回归结果的衡量,故总的衡量方法为:
所以,回归 loss 为:
1.2.1.8 YOLOv7
详细介绍见 本文
论文:YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors
代码:https:// github.com/WongKinYiu/yolov7
出处:暂无
作者:Chien-Yao,Alexey AB (和 YOLOv4 同)
时间:2022.07
从优化方法、优化模块等方面入手,通过提高训练过程的 cost 来提高检测效果,但不会提高推理过程的 cost。
YOLOv7 的思路是什么:
- 重参数化和 label assignment 对网络的效果都比较重要,但近来提出的方法中,或多或少会有些问题
- YOLOv7 会从发现的这些问题入手,并提出对应的解决方法
在正文前,YOLOv7 也总结了一下现有的 SOTA 实时目标检测器,大多基于 YOLO 和 FCOS,要想成为一个优秀的实时检测器,一般需要具有如下几个特点,并且主要从 4/5/6 三点来提出问题并解决:
- a faster and stronger network architecture
- a more effective feature integration method [22, 97, 37, 74, 59, 30, 9, 45]
- a more accurate detection method [76, 77, 69]
- a more robust loss function [96, 64, 6, 56, 95, 57]
- a more efficient label assignment method [99, 20, 17, 82, 42]
- a more efficient training method.
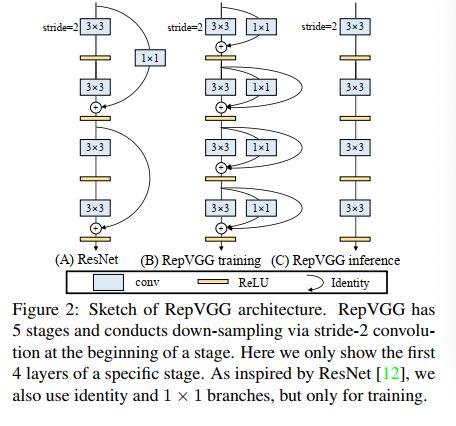
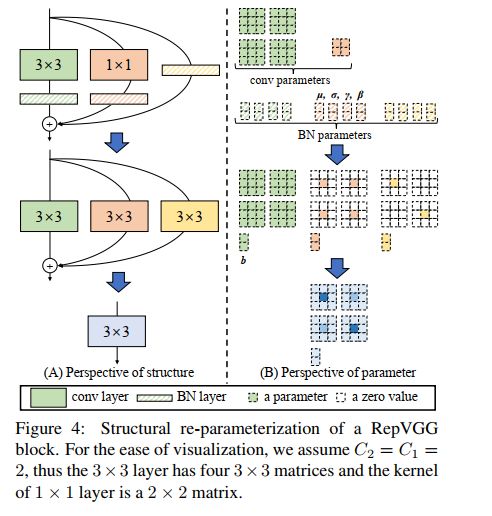
“结构重参数化” 的实质:训练时的结构对应一组参数,推理时我们想要的结构对应另一组参数,只要能把前者的参数等价转换为后者,就可以将前者的结构等价转换为后者。
1.2.2 SSD
详细介绍见 本文
论文:SSD: Single Shot MultiBox Detector
出处:ECCV 2016
贡献:实现了一个可以端到端训练的 anchor-based 单阶段检测器,可以达到实时检测的速度
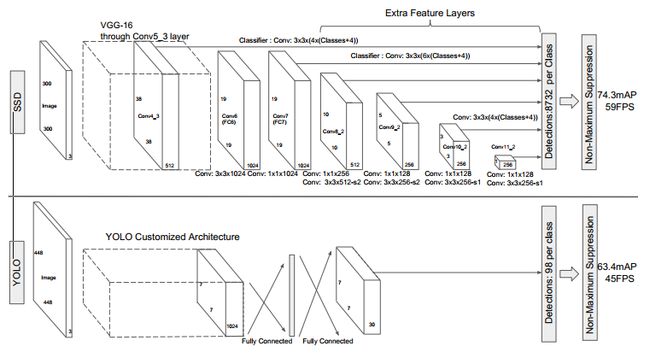
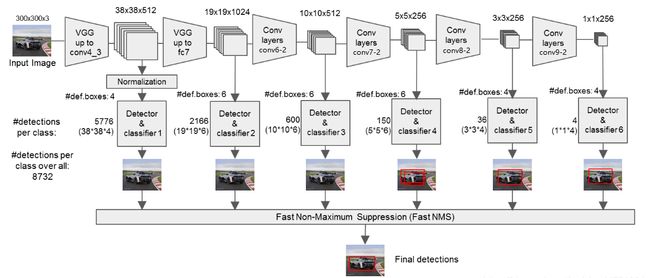
SSD 的详细结构如下图:假设输入为 300x300经过 VGG 网络
- 第一层特征:使用 conv4-3 的结果,38x38x512,用作第一层特征
- 第二层特征:使用 fc-7 的结果,19x19x1024,用作第二层特征
- 第三层特征:使用 conv8-2 的结果,10x10x512,用作第三层特征
- 第四层特征:使用 conv9-2 的结果,5x5x256,用作第四层特征
- 第五层特征:使用 conv10-2 的结果,3x3x256,用于第五层特征
- 第六层特征:使用 conv11-2 的结果,1x1x256,用于第六层特征
在这六层特征图上,如何布 anchor 呢:
- SSD 的这六层特征,可以在每层分别预测不同大小的目标。比如在大特征图上检测较小的目标,在小特征图上检测较大的目标
- anchor 尺度:每层特征图上 anchor 的尺度是不同的,第一层特征图使用的 anchor 尺度为 s m i n = 0.2 s_{min}=0.2 smin=0.2,第六层特征图使用的 anchor 尺度为 s m a x = 0.9 s_{max}=0.9 smax=0.9,意味着最底层尺度为 0.2,最高层尺度为 0.9,且其间的所有层具有相同的间隔。
- anchor 纵横比:纵横比为 [1, 2, 3, 1/2, 1/3]
- 每层特征图上都会生成大量的 anchor,假设每个点上生成 k 个 anchor
- 对每个 anchor 都要预测类别(包括背景)+ 位置,如果某层特征图大小为 m × n m \times n m×n,则共需要预测的特征值为 m × n × k × ( k + 4 ) m \times n \times k \times (k + 4) m×n×k×(k+4)
SSD 模型在base network 的最后添加了一系列特征层,能够预测不同尺度、纵横比的预测框的偏置和分类置信度得分。
使用 VOC 2007 测试集进行测试,可知SSD 输入 300x300 的情况下比 YOLO 输入448x448 情况下的效果更好,且速度更快。
SSD 当时是针对 YOLOv1 的局限性而提出来的,SSD 的特点如下:
- anchor-based:SSD 也是将图像分割成网格单元,在每个网格单元中,会生成一组多尺度和纵横比的 anchor,是 anchor-based 的方法,每个 anchor 都会学习 4 个回归偏移和 (C+1) 个分类概率。
- 多尺度预测:SSD 会在多级特征图上进行目标预测,每个尺度的特征图负责一定尺度的目标,可以看做 FPN 思想的前身
- 端到端的训练:SSD 是单阶段的 anchor-based 目标检测器,不需要额外的 region proposal,在后面几层特征图上直接布 anchor,来实现对不同大小目标的检测
- 高效:且具有实时的推理能力
1.2.3 RetinaNet
详细介绍见 本文
论文:Focal Loss for Dense Object Detection
代码:https://github.com/facebookresearch/Detectron
出处:原始论文出自 ICCV2017
贡献:提出了单阶段和双阶段目标检测器效果差异的根源所在,即正负样本不平衡,并提出了 Focal loss,提高难例和正例对 loss 的贡献,处理但阶段目标检测器的正负样本严重不平衡的问题。
作者提出单阶段目标检测器和两阶段目标检测器效果差异的最重要原因:正负样本不平衡
当时以 YOLOv1 和 SSD 等为代表的单阶段目标检测的方法,虽然很快,但效果不尽如意,所以 RetinaNet 的作者就探索两种方法的效果差距究竟来源于哪里。
- 双阶段检测器:使用 RPN 网络来生成候选框,大约保留 1-2k,该网络能区分正负样本,保留下更多的正样本,过滤掉大量的背景样本,来保持前景和背景的样本均衡(如 1:3)
- 单阶段检测器:在特征图上均匀的部署很多 anchor,大约 100k 左右,大量的都是负样本
Focal loss:只支持 0 或 1 这样的离散类别 label 求 loss
Focal loss 是如何解决正负/难易样本不平衡:
- 正样本loss增加,负样本loss减小
- 难样本loss增加,简单样本loss减小
一般分类时候通常使用交叉熵损失:
C r o s s _ E n t r o p y ( p , y ) = { − l o g ( p ) , y = 1 − l o g ( 1 − p ) , y = 0 Cross\_Entropy(p,y)= \begin{cases} -log(p), & y=1 \\ -log(1-p), & y=0 \end{cases} Cross_Entropy(p,y)={−log(p),−log(1−p),y=1y=0
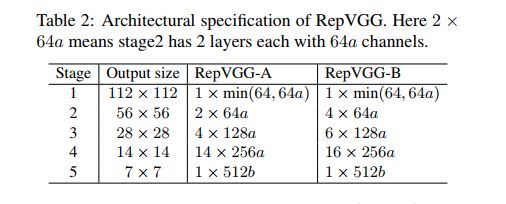
但由于上面说的单阶段检测器的 anchor 生成策略,很容易导致负样本占大多数,在训练的过程中,正负样本都会参与模型的训练
。
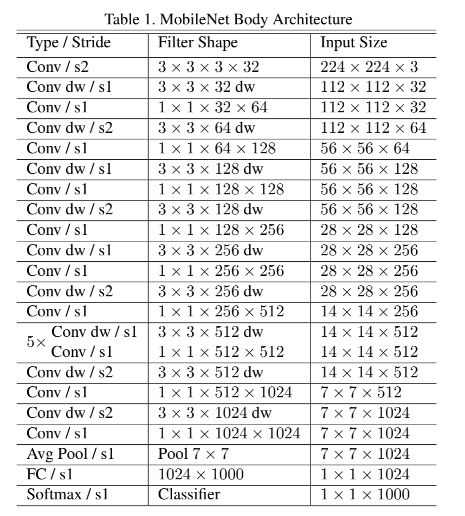
假设总的样本数为 N,正样本为 m,负样本为 n,N=m+n,严重不平衡时,m< Loss 函数: 为了解决正负样本数量不平衡的问题,我们经常在二元交叉熵损失前面加一个参数 α ∈ [ 0 , 1 ] \alpha \in [0, 1] α∈[0,1]。负样本出现的频次多,那么就降低负样本的权重,正样本数量少,就相对提高正样本的权重。 因此可以通过设定 α \alpha α 的值来控制正负样本对总的loss的共享权重。 α \alpha α取比较小的值来降低负样本(多的那类样本)的权重。即: C r o s s _ E n t r o p y ( p , y ) = { − α l o g ( p ) , y = 1 − ( 1 − α ) l o g ( 1 − p ) , y = 0 Cross\_Entropy(p,y)= \begin{cases} -\alpha log(p), & y=1 \\ -(1-\alpha) log(1-p), & y=0 \end{cases} Cross_Entropy(p,y)={−αlog(p),−(1−α)log(1−p),y=1y=0 其中: α : 1 − α = n : m \alpha : 1-\alpha = n : m α:1−α=n:m,也就是用这种方法来平衡,单单考虑 α \alpha α 的话, α = 0.75 \alpha=0.75 α=0.75 时是最优的(后面加上难易样本的平衡后, α = 0.25 \alpha=0.25 α=0.25 是最优的) 虽然平衡了正负样本的数量,但实际上,目标检测中大量的候选目标都是易分样本。这些样本的损失很低,但是由于数量极不平衡,易分样本的数量相对来讲太多,最终主导了总的损失。 因此,Focal loss 作者认为易分样本(即,置信度高的样本)对模型的提升效果非常小,模型应该主要关注与那些难分样本 。一个简单的想法就是只要我们将高置信度样本的损失降低一些, 也即是下面的公式: 当 γ = 0 \gamma=0 γ=0 时,即为交叉熵损失函数,当其增加时,调整因子的影响也在增加,实验发现为2时效果最优。 假设取 γ = 2 \gamma=2 γ=2,如果某个目标置信得分 p=0.9,即该样本学的非常好,那么这个样本的权重为 ( 1 − 0.9 ) 2 = 0.001 (1-0.9)^2=0.001 (1−0.9)2=0.001,损失贡献降低了 1000 倍。 为了同时平衡正负样本问题,Focal loss还结合了加权的交叉熵loss,所以两者结合后得到了最终的Focal loss: F o c a l _ L o s s = { − α ( 1 − p ) γ l o g ( p ) , y = 1 − ( 1 − α ) p γ l o g ( 1 − p ) , y = 0 Focal\_Loss = \begin{cases} -\alpha (1-p)^\gamma log(p), & y=1 \\ -(1-\alpha) p^\gamma log(1-p), & y=0 \end{cases} Focal_Loss={−α(1−p)γlog(p),−(1−α)pγlog(1−p),y=1y=0 取 α = 0.25 \alpha=0.25 α=0.25 在文中,即正样本要比负样本占比小,这是因为负样本易分。 单单考虑 α \alpha α 的话, α = 0.75 \alpha=0.75 α=0.75 时是最优的。但是将 γ \gamma γ 考虑进来后,因为已经降低了简单负样本的权重, γ \gamma γ 越大,越小的 α \alpha α 结果越好。最后取的是 α = 0.25 , γ = 2.0 \alpha=0.25,\gamma=2.0 α=0.25,γ=2.0 RetinaNet 网络结构如下: RetinaNet 是一个由 backbone + subnetworks 构成的统一的网络结构,backbone 后面跟了一个 neck 网络 FPN,然后后面跟了两个并行子网络,分别用于分类和回归。 详细介绍见 本文 论文:Objects as Points 代码:https://github.com/xingyizhou/CenterNet 发布时间:2019.4.16 出处:CVPR 2019 还有一种特殊的单阶段检测器,通过预测目标的关键点并将预测到的关键点进行分组来获得目标的边界框。 CenterNet 的贡献: CenterNet的缺点: CenterNet 和单阶段或双阶段检测器的区别主要来自两个方面: CenterNet 没有 anchor这个概念,只负责预测物体的中心点,所以也没有所谓的 box overlap 大于多少多少的算 positive anchor,小于多少算 negative anchor 这一说,也不需要区分这个 anchor 是物体还是背景,因为每个目标只对应一个中心点,这个中心点是通过 heatmap 中预测出来的,所以不需要NMS再进行来筛选。 CenterNet 的输出分辨率的下采样因子是 4,比起其他的目标检测框架算是比较小的 (Mask-Rcnn最小为16、SSD为最小为16)。之所以设置为 4 是因为 centernet 没有采用 FPN 结构,因此所有中心点要在一个 Feature map 上出,因此分辨率不能太低。 CenterNet 网络结构:CenterNet 提到了三种用于目标检测的网络,这三种网络都是编码解码 (encoder-decoder) 的结构(ResNet、DLA、hourglass),在 backbone 模型的最后输出部分都是加了三个网络构造来输出预测值,默认是80个类、2个预测的中心点坐标、2个中心点的偏置。 HeatMap 是如何生成的:每一个类别都有一张 heatmap,每一张 heatmap 上,若某个坐标处有物体目标的中心点,即在该坐标处产生一个 keypoint (用高斯圆表示) 为什么要用高斯核来处理中心点: Heatmap 上的关键点之所以采用二维高斯核来表示,是由于对于在目标中心点附近的一些点,其预测出来的 box 和 gt_box 的 IoU 可能会大于 0.7,不能直接对这些预测值进行惩罚,需要温和一点,所以采用高斯核。 CenterNet 网络有三个输出,那么如何将这些输出转为直观的检测框信息呢,也就是如何从 point 到 b-box? 主要通过最大池化操作(类似 NMS)后在 heatmap 上寻找 topk 个最大值,即可能为物体中心的索引。然后根据这 topk 个中心点,寻找其对应的类别、宽高和 offset 信息。 CenterNet 的 NMS 方法: CenterNet 的 NMS,是寻找某点与其周围的八个点之间最大值,作为其 NMS 的极大值。那么该操作可以使用最简单的 3x3 的 MaxPooling 实现。 3x3 大小的 kernel 加上特征图和输入图像之间的 stride=4,相当于输入图像中每 12x12 大小的区域都不会有重复的中心点,想法非常简单有效! 在预测阶段,首先针对一张图像进行下采样,随后对下采样后的图像进行预测,对于每个类在下采样的特征图中预测中心点,然后将输出图中的每个类的热点单独地提取出来。检测当前热点的值是否比周围的八个近邻点(八方位) 都大 (或者等于),然后取100个这样的点,采用的方式是一个 3x3 的 MaxPool,类似于 anchor-based 检测中 nms 的效果。 Loss 函数: 1、中心点损失 hm: 该 Focal loss 函数是针对 CenterNet 修正而来的损失函数,和 Focal Loss 类似,对于 easy example 的中心点,适当减少其训练比重也就是loss值。 ( 1 − Y ^ x y z ) α (1-\hat{Y}_{xyz})^{\alpha} (1−Y^xyz)α 和 ( Y ^ x y z ) α (\hat{Y}_{xyz})^{\alpha} (Y^xyz)α 的作用: 限制 easy example 导致的梯度更新被易区分的点所主导的问题 当 Y x y z = 1 Y_{xyz}=1 Yxyz=1 的时候, 假如 Y ^ x y z \hat{Y}_{xyz} Y^xyz 接近1的话,说明这个是一个比较容易检测出来的点,那么 ( 1 − Y ^ x y z ) α (1-\hat{Y}_{xyz})^{\alpha} (1−Y^xyz)α 就相应比较低了。 当 Y x y z = 1 Y_{xyz}=1 Yxyz=1 的时候,而 Y ^ x y z \hat{Y}_{xyz} Y^xyz 接近0的时候,说明这个中心点还没有学习到,所以要加大其训练的比重,因此 ( 1 − Y ^ x y z ) α (1-\hat{Y}_{xyz})^{\alpha} (1−Y^xyz)α 就会很大, α \alpha α是超参数,这里取2。 当 Y x y z = 0 Y_{xyz}=0 Yxyz=0 的时候,预测的 Y ^ x y z \hat{Y}_{xyz} Y^xyz 理论上也要接近于0,但如果其预测的值 Y ^ x y z \hat{Y}_{xyz} Y^xyz 接近于1的话, ( Y ^ x y z ) α (\hat{Y}_{xyz})^{\alpha} (Y^xyz)α 的值就会比较大,加大损失,即增加这个未被正确预测的样本的损失。 ( 1 − Y x y z ) β (1-Y_{xyz})^{\beta} (1−Yxyz)β 的作用: 看一下官方的这张图可能有助于理解: 传统的基于 anchor 的检测方法,通常选择与标记框IoU大于 0.7 的作为 positive,相反,IoU 小于 0.3 的则标记为 negative,如下图a。这样设定好 box 之后,在训练过程中使 positive 和 negative 的 box 比例为 1:3 来减少 negative box 的比例 (例如 SSD 没有使用 focal loss)。 而在 CenterNet 中,每个中心点对应一个目标的位置,不需要进行 overlap 的判断。那么怎么去减少 negative center pointer 的比例呢?CenterNet 是采用 Focal Loss 的思想,在实际训练中,中心点的周围其他点 (negative center pointer) 的损失则是经过衰减后的损失(上文提到的),而目标的长和宽是经过对应当前中心点的 w 和 h 回归得到的: 2、目标中心的偏置损失 reg: 因为对图像进行了 R=4 的下采样,这样的特征图重新映射到原始图像上的时候会带来精度误差,因此对于每一个中心点,额外采用了一个 local offset 去补偿它。所有类 c 的中心点共享同一个offset prediction,这个偏置值(offset)用L1 loss来训练: 这个偏置损失是可选的,我们不使用它也可以,只不过精度会下降一些。 仅仅在关键点位置 p ~ \widetilde{p} p 上实行有监督行为,其他位置被忽略。 3、目标大小的损失 wh: 我们假设 ( x 1 ( k ) , y 1 ( k ) , x 2 ( k ) , y 2 ( k ) ) (x_1^{(k)}, y_1^{(k)}, x_2^{(k)}, y_2^{(k)}) (x1(k),y1(k),x2(k),y2(k))为目标 k ,所属类别为c ,它的中心点为: p k = ( x 1 ( k ) + x 2 ( k ) 2 , y 1 ( k ) + y 2 ( k ) 2 ) p_k = (\frac{x_1^{(k)}+x_2^{(k)}}{2},\frac{y_1^{(k)}+y_2^{(k)}}{2}) pk=(2x1(k)+x2(k),2y1(k)+y2(k)) 使用中心点去预测所有目标的中心点,然后回归每个目标 k 的目标大小: s k = ( x 2 ( k ) − x 1 ( k ) , y 2 ( k ) − y 1 ( k ) ) s_k = (x_2^{(k)}-x_1^{(k)},y_2^{(k)}-y_1^{(k)}) sk=(x2(k)−x1(k),y2(k)−y1(k)) 损失函数:L1 loss 4、整体损失 整体的损失函数为物体损失、大小损失与偏置损失的和,每个损失都有相应的权重。 详细介绍见 本文 论文:FCOS: Fully Convolutional One-Stage Object Detection 代码:https://github.com/aim-uofa/AdelaiDet/tree/master/configs/FCOS-Detection 出处:ICCV2019 贡献:将类似 FCN 的全卷积的方法应用到了目标检测任务上,能够实现端到端的单阶段预测;也是第一个使用逐个像素点预测的目标检测方法,并提出了 centerness 分支,在推理阶段抑制低质量框并提升检测效果。 和 CenterNet 的出发点类似,当时占据统治地位的大都是基于 proposal 和 anchor 的方法,但这些方法有一些共同的缺陷: FCOS 的主要过程: FCOS 的测试: 虽然说很多单阶段目标检测器是 anchor-free 的,但其实可以将那些 point 看成 anchor point,只是不像 anchor box 那种必须有一个框才能称为 anchor,所以我们这里将 anchor-free 方法中的 point 也称为 anchor point,而将 anchor-based 方法中的 bbox 称为 anchor box。 详细介绍见 本文 论文:Focal Loss for Dense Object Detection 代码:https://github.com/facebookresearch/Detectron 出处:原始论文出自 ICCV2017 在每个位置设定多个 anchor,使用 IoU 来区分前景、背景框,IoU 大于某个阈值(如0.5)的为正样本,小于某个阈值(如0.3)的为负样本,其他框忽略。 缺点:IoU 阈值需要人工选择 详细介绍见 本文 论文:FCOS: Fully Convolutional One-Stage Object Detection 代码:https://github.com/aim-uofa/AdelaiDet/tree/master/configs/FCOS-Detection 出处:ICCV2019 FCOS 中,是以 anchor point 作为特征点,将每个点当做训练样本,使用点是否在框内来区域前景、背景点 缺点:需要设定阈值参数,且这些确定的规则虽然对大多数目标适用,但对一些 outer 的目标是不使用的,所以,对不同的目标应该用不同的规则。 详细介绍见 本文 论文:Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection 代码:https://github.com/open-mmlab/mmdetection/tree/master/configs/atss 出处:CVPR2020 ATSS 是一种 anchor 正负划分的方式,不是一种目标检测框架,所以需要嵌入其他目标检测框架中进行目标检测,可以嵌入 FCOS 和 RetinaNet 的结构中 贡献:使用实验证明了单阶段 anchor-based 方法和 anchor-free 方法的效果差距的最主要原因在于正负样本的划分方式(对比 FCOS 和 RetinaNet)。Adaptive Training Sample Selection (ATSS) ,根据目标的统计信息,自动选取正负样本,无任何超参数。 分析 anchor-based 和 anchor-free 方法效果不同的本质原因: 在训练检测器时,首先要定义正负样本来进行分类,其次要对正样本进行回归,ATSS 中利用实验证明了 FCOS 是对 RetinaNet 在正负样本定义上的优化,才取得了效果提升。 该结论说明,正负样本选择的方法对 anchor-free 和 anchor-based 方法的结果的差别起到了很重要的作用。 ATSS 如何划分正负样本: 上面为什么使用 anchor 和 object 的中心点距离来选择候选框? 为什么要使用均值和标准差这些统计结果来非固定的阈值? 这里使用的是 k × l k\times l k×l 个 anchor 的 IoU 的统计信息,也可以看做是选择了 level。 本文的阈值是一个统计结果,如图 3(a) 有一个高的阈值,这是因为这里的候选框质量都很高,如图3(b) 有一个低的阈值,说明这里的框的质量都不高,如果使用高阈值的话,会把绝大部分的框都滤掉,不合适,所以使用统计的量作为阈值是一个可取的方式。 IoU 的方差决定了由 FPN 的哪几个 level 来负责检测该目标: FPN 层的一个很大的作用就是分而治之,比如较大的目标是由较深的层来负责: 综上也可知,IoU 阈值和 IoU 的方差有关 详细介绍见 本文 论文:FreeAnchor: Learning to Match Anchors for Visual Object Detection 代码:https://github.com/zhangxiaosong18/FreeAnchor 出处:NIPS2019 贡献点: Anchor-based 方法的 label assignment,一般使用 IoU 来实现,大于某个阈值的 anchor 为正样本,小于某个阈值的 anchor 为负样本,每个 anchor 的 assignment 是独立的,但手工选取的参数肯定不是最优的。 原因有两点: 本文提出了一种基于学习策略的 label assignment 方法,从 3 个方面来分析: 基于上述分析,作者将 object-anchor 的匹配问题,构造成了一个最大似然估计 maximum likelihood estimation(MLE)过程,即从一系列 anchor 中选择优质的 anchor 并分配给每个 gt。 MLE 的过程,就是最大化一个似然估计,保证每个 gt 至少有一个 anchor 是同时具有高分类得分和定位得分的。其他很多分类误差大或定位误差大的 anchor 被分为 background。在训练过程中,似然估计也就变成了 loss 函数。 如何将检测的 loss 转换成极大似然估计的形式: 上面的 2 式,其实就从 MLE 的角度,同时考虑的分类和回归,但一般的方法也就缺乏了一点:如何优化 matching matrix C i j C_{ij} Cij,因为一般都是直接使用 IoU 来决定该 matrix 的值。 所以,FreeAnchor 的网络学习的是什么,就是这个 matrix C i j C_{ij} Cij 如何学习这个最优的 matching matrix C i j C_{ij} Cij 呢: 首先,使用 IoU,选出 anchor 集合中的 top-n anchors(也就是缩小了 anchor 的可选择范围,但还是可以选择的,而非直接指定确定的 anchor 来匹配某个 gt) 接着,通过最大化 detection customized likelihood 来让网络学习最优的 gt-anchor 匹配 其次,为了优化 recall 效果,对每个真值,都至少需要一个 anchor,且该 anchor 对应的分类和回归结果是和该 gt 的真值很相近的(也就是该 anchor 很优质),则该目标函数可以写为: 再次,为了优化 precision 效果,分类器要能够把定位差的 anchor 分配到 background 类上去,则该目标函数如下所示,其中, P { a j ∈ A _ } = 1 − max i P { a j → b i } P\{a_j \in A\_\}=1-\text{max}_iP\{a_j \to b_i\} P{aj∈A_}=1−maxiP{aj→bi} ,表示 a i a_i ai 没有和任何 gt 匹配上的概率, P { a j → b i } P\{a_j \to b_i\} P{aj→bi} 表示 anchor a j a_j aj 能够正确预测目标 b i b_i bi 的概率: 然后,为了更好的适配 NMS 过程, P { a j → b i } P\{a_j \to b_i\} P{aj→bi} 需要满足如下三个特性,分段函数如图 2 所示: 最后,detection customized likelihood 定义如下,通过优化这个似然函数,可以同时最小化 recall 和 precision 的概率,实现在训练过程中无需手动匹配 gt-anchor: 为了实现 learning-to-match 的方法,公式 5 可以被转换成 detection customized loss function ,公式如下: 训练早期,由于所有参数都是随机初始化而来,所以所有 anchor 的置信度都比较低,而得分较高的 anchor 越有利于模型的训练,所以,作者使用了 Mean-max 函数,来选择 anchor。如图 3 所示,Mean-max 函数是近似 mean 函数的,也就是说,几乎所有的 anchor 都会用于训练: Mean-max 其实可以看做先 mean,最后 max 的情况。刚开始所有的 anchor 其实都不太准,所以取平均,随着训练的进行,一些 anchor 的置信度会逐步增加,最后肯定会有一个最大的 anchor 作为最终的选择。即随着训练,从 mean 过渡到 max,然后会给每个 gt 选择一个最优的 anchor。 使用 Mean-max 函数代替公式 6 中的 max 函数,并添加平衡因子和使用 Focal loss。 FreeAnchor 检测器最终的 detection customized loss 函数公式如下: 详细介绍见 本文 论文:AutoAssign: Differentiable Label Assignment for Dense Object Detection 代码:https://github.com/Megvii-BaseDetection/AutoAssign 出处:被 ECCV2020 拒 贡献:提出了让网络自主学习 anchor 正负的方法,首先提出了一种与类别相关且对不同位置使用不同权重的 label assign 方法,能够同时优化空间和尺度的 label assignment。具体来说,就是引入了两个加权系数:① Center weighting 用于学习不同类别的先验,让每个类别有自己的正样本采样方式;② confidence weighting 用于学习每个位置的前景权重和背景权重 现有的标签分配方法的不足: 其他方法是怎么解决上述问题的: 其他方法的缺点: AutoAssign 的做法:AutoAssign 的正负样本分配,可以看做把处于目标上的样本点看做正样本,把虽然在 bbox 内但不属于目标本身的样本点看做负样本(AutoAssign 认为在真实目标上采样,肯定比在背景上采样效果更好)。 AutoAssign 这样做的优势:让标签的分配依赖于数据先验的同时,也能对不同的类别进行不同的自适应,避免了人为选定参数,如 IoU 阈值、anchor 分布、top-k 等。 AutoAssign 的两个特点: 将每个尺度的每个位置平等看待,不直接划分正负样本:AutoAssign 的框架是建立在 FCOS 之上的,对每个 location 都平等对待,每个 location 都有正样本属性和负样本属性(即体现在原文中的w+ 和w-)。 也就是说,在优化的过程中,有些样本会同时受到来自它为正样本的监督和负样本的监督,两者利用 w + w^+ w+ 和 w − w^- w− 来平衡配比,此外,不在任何 gt 框里的 location 其正样本属性 w+ 必然为0,也就是那些位置必然是background。 联合优化分类和回归(将回归函数也处理成了似然形式): L i ( θ ) = L i c l s ( θ ) + λ L i l o c ( θ ) = − l o g ( P i ( θ ) ) L_i(\theta) = L_i^{cls}(\theta)+\lambda L_i^{loc}(\theta) =-log(P_i(\theta)) Li(θ)=Licls(θ)+λLiloc(θ)=−log(Pi(θ)) 加权机制: 从 label assignment 的角度来看,AutoAssign 究竟做了什么: 其他 label assignment 的方法对不同的数据集的提升可能不太稳定,但 AutoAssign 可以根据不同的数据来动态调整,无需额外的手动调节和参数设置,就能达到约 1% 的提升。 详细介绍见 本文 论文:Probabilistic Anchor Assignment with IoU Prediction for Object Detection 代码:https://github.com/open-mmlab/mmdetection/tree/master/configs/paa 出处:ECCV2020 贡献:提出了基于概率统计的 anchor assignment 的方法,使用 anchor 得分来自适应的区分 anchor 的正负。使用(预测 anchor 和 gt 的 IoU * 预测的Classification score) 来作为 NMS 框排序衡量标准。 如何计算 anchor 得分呢: 此处作者考虑 anchor assignment 策略有三点需注意: 作者如何实现 anchor score: 对上面的 score 使用负对数形式后得到: 为什么要使用负对数? anchor score 越高,越有可能是正样本,anchor score 越高,则要求分类得分和定位得分都越大,换个说法,要求分类 loss 和定位 loss 都越小。所以,使用负对数能够将得分转化成 loss 的形式,最大化 anchor score ,则就是最小化 anchor score 的负对数结果。 由于 anchor assignment 的目的是将一堆 anchor 区分为正负样本,故使用高斯混合模型来对 anchor score 进行建模,得到 anchor score 后,可以使用 EM 算法来求解这个高斯混合模型的似然结果: PAA 的整体过程: 详细介绍见 本文 论文:Optimal Transport Assignment for Object Detection 代码:https://github.com/Megvii-BaseDetection/OTA 出处:CVPR2021 贡献: RetinaNet 使用 IoU 来实现,FCOS 根据每个点是否在 gt box 内部来确定其正负。 这些方法忽略了一个问题:不同大小、形状、遮挡程度的目标,其 positive/negative 的判定条件应该是不同的。 所以就有一些方法使用动态的分配方法,来实现 label assignment。 作者认为,独立的给每个 gt 分配 pos/neg 不是最优的方法,缺失了上下文信息,当处理那些模棱两可的 anchor 时(如图 1 中的红色点,一个点处于多个 gt 中),上面的方法是靠手工的特征来选定属于哪个 gt 的(如 max-IoU、min-Area 等)。 CNN 的方法中,其实是 one-to-many 的形式,也就是一个 gt 会对应多个 anchor。 本文作者为了从 global 的层面来实现 CNN 中的 one-to-many assignment,将 label assignment 问题变成了一个 Optimal Transport(OT)问题(线性规划的一个特殊形式)。 OT 是这样的一个问题: 把 OT 放到目标检测的问题中,假设有 m 个 gt,n 个 anchor(所有 FNP 层的 anchor 之和) 把 gt 看做 positive labels 的供货商,供应 label,能够对 k anchor 供应 positive label,也就是每个 gt 对 k 个 anchor 负责( s i = k , i = 1 , 2 , . . . , m s_i=k, i=1,2,...,m si=k,i=1,2,...,m) 把 anchor 看做需求方,需要一个label( d j = 1 , j = 1 , 2 , . . . , n d_j=1, j=1,2,...,n dj=1,j=1,2,...,n) 把一个 positive label 从 g t i gt_i gti 传递到 anchor a j a_j aj 的花费为 c f g c^{fg} cfg,则该花费就是 cls 和 reg loss 的加权和(分类可用 Focal loss,回归可用 IoU loss 等),这里是点对点的 loss 之和,也就是所有的 gt 和所有的 anchor 分别点对点求 loss: 除过 positive assignment,还有很大一部分 anchor 是负样本,所以还引入了一个供应商——背景,来提供 negative labels。 标准的 OT 问题中,供货商和需求方的数量应该是一样的,所以,背景可以提供的 negative labels 的数量就是 n − m × k n-m \times k n−m×k,n 为 anchor 格式,m 为 gt 个数 将一个 negative label 从 background 传递到 anchor 的花费如下,只有分类的 loss: 将 c b g ∈ R 1 × n c^{bg}\in R^{1\times n} cbg∈R1×n 和 c f g ∈ R m × n c^{fg} \in R^{m \times n} cfg∈Rm×n concat 起来,就得到了最终的花费 c ∈ R ( m + 1 ) × n c \in R^{(m+1) \times n} c∈R(m+1)×n。其中 m 个 gt, n 个 anchor。 每个供应商(gt 或 background)负责的 anchor 个数为 s i s_i si,以 m 为区分,m+1 表示的就是 background: 有了花费、供应商、需求方后,最优传递方案 π* 可以使用 off-the-shelf Sinkhorn-Knopp Iteration 方法解该 OT 问题来得到。 具体图示见图 2 中的 cost matrix,每行为一个 gt,每个 gt 会分别计算其和每个 anchor 的花费,组成最终的 cost matrix。 得到了 π* 之后,可以通过把每个 anchor 分配到能给他供货最多(即提供 label 数量最多)的 gt 上去来实现最优 label assignment。 OT 的计算只需要矩阵乘法,可以使用 GPU 来加速,提高了约 20% 的训练时间,在测试时候是无多消耗的。 OTA 的结构如下: OTA 的过程如下: SimOTA 是 YOLOX 中使用的 label assignment 的方式。都是旷世提出的方法。 在 OTA 中,总结了一个好的 label assignment 的方法一般有四个优点,且 OTA 也都满足了: OTA 将 label assignment 问题从 global 层面出发并看成了一个最优传输的问题,但 OTA 有一个问题,它需要使用 Sinkhorn-Knopp algorithm 来优化,这会增加 25% 的训练时间,假设使用 300 epoch,那增加的时长是不容小觑的。 所以孙剑等人又提出了 SimOTA,将 OTA 的优化过程简化了——dynamic top-k strategy,使用该优化策略得到一个大概的解决方案。 SimOTA 是如何简化的? SimOTA 的优势: 详细介绍见 本文 NMS 及其变体在边缘检测、关键点检测和目标检测等视觉任务上都有广泛的使用。主要用于剔除和极大值重叠率过大的检测结果。 使用场景: NMS 的分类: NMS 的过程如下: NMS 方法的不足 由于 NMS 的剔除方法过于暴力,可能剔除掉真正定位准确的框,导致保留的框不准确或漏检的问题,而 soft-NMS 不直接删除 IoU 大于阈值的框,而是降低其分类得分,用以缓解漏检的情况。 1、NMS 的处理方法: 2、Soft NMS 的处理方法: 具体是如何降低得分的呢(只降低 IoU > 阈值的框的得分): 第一种加权方式:线性加权,当 IoU 越大,(1-IoU) 越小,则和 s i s_i si 相乘后越小,修正后的分类得分越小 所以作者使用高斯的方式来对得分进行修正: 第二种加权方式:高斯加权: 优势: 不足: 由于 NMS 的三个问题: soft NMS 通过降低距离近的框的得分,而非直接剔除该框的方法,缓解了第一个问题,所以 Softer NMS 被提出,以 “标注框并非准确,会有一定不确定性” 为前提,来通过定位的方差投票来进行位置修正。 Softer NMS = soft NMS + variance voting 1、针对边分布不确定性问题:使用高斯分布来表示框的每个边的位置,使用 KL-Loss 来学习位置的分布(这个分布就包括位置可不确定性——即方差) 为了通过位置来估计出位置得分,会预测一个概率分布,而非 bbox 的位置。 预测的概率分布简化为一个高斯分布: 其中: 真实的位置也可以被建模为一个特殊的高斯分布, σ → 0 \sigma \to 0 σ→0, 就是 Dirac delta 分布: 其中: KL Loss 如何计算: 上面将预测结果和真实 label 建模后,就可以使用 N 个采样点来估计出参数 Θ ^ \hat{\Theta} Θ^,最小化预测和真实分布的 KL 距离: KL 散度是用于框位置的回归的: 当网络预测一个较大的方差 σ 2 \sigma^2 σ2 时, L r e g L_{reg} Lreg 会很小,位置 x e x_e xe 的估计会更准确。如上图 4 所示。 由于 L r e g L_{reg} Lreg 不依赖于后两项,则有如下规律: 当 σ = 1 \sigma=1 σ=1 时,KL loss 演变成一个规范的 Euclidean loss: KL loss 的三个优势: 2、针对分类得分和定位得分使用未对齐的问题:使用方差投票 Var voting:得分修正(soft NMS )+ 位置修正(给距离候选框近的框分配更高的权重,其不确定性更小) 第一步:首先进行 soft NMS: Soft NMS:对大于 IoU 阈值的框得分抑制(线性和高斯两种方式,高斯更优),小于 IoU 阈值的框得分不变 soft NMS 认为和候选框距离越近的框,越有可能是”假正”,对应分数的衰减应该更严重,所以对得分进行衰减。 衰减方式 1:使用1-IoU与得分的乘积作为衰减后的值:参数为 $ N_t=0.3$ 第二步:完成了 soft-NMS 后,对得到的边框 b m b_m bm 进行基于网络学习到的方差进行修正。 预测结果为: ( x 1 , y 1 , x 2 , y 2 , s , σ x 1 , σ y 1 , σ x 2 , σ y 2 ) (x_1, y_1, x_2, y_2, s, \sigma_{x_1}, \sigma_{y_1}, \sigma_{x_2}, \sigma_{y_2}) (x1,y1,x2,y2,s,σx1,σy1,σx2,σy2) 新的坐标计算如下, x i x_i xi 是第 i i i 个框的坐标( σ t \sigma_t σt 是可调节参数): 首先,选择出分类得分最大的框 b b b 然后,对所有和 b b b 存在 IoU 交集的框 ( I o U ( b i , b ) IoU(b_i, b) IoU(bi,b) >0),计算权值 p i p_i pi 最后,根据权值,来更新 b b b 的坐标(四个坐标分别更新) 作者给距离真值更近但分类得分低的框权重更高。 有两种邻域框会被降权重: 分类得分不参与投票,因为低分类得分可能有高位置得分。 首先,由于一般的 NMS 是用分类分数来主导一个框的去留,想当然的选择得分高的框作为最优的框,忽略了得分高并不一定定位准的现象。 其次,在整个重复去留的过程中,没有一个定位质量的衡量标准,所以最终回归得到的框可解释性较差,如图 1b 所示,可能经过多次迭代反而得到了更不好的框。 基于上述背景,IoU-Net 被提出了,目的是让网络和关系分类得分一样关心定位得分。 IoU-Net 首先通过实验得到了两个结论: IoU 和 classification confidence 反而没有强关联,和 localization confidence 有强关联: 作者分析了以 IoU 为横轴,分类得分和定位得分(预测的 IoU 作为定位得分)为纵轴的散点图,发现了 IoU 和 localization confidence 有强关联,IoU 和 classification confidence 反而没有强关联 很多 IoU>0.9 的框被 NMS 滤掉了: 作者又分析了在使用 NMS 之前和之后,保留下来的框和 gt 的 IoU 值,这些框是依据 IoU 聚拢的,当多个框对应一个真值框的时候,只将 IoU 最大的那个框认为是 positive 的。有很多 IoU>0.9 的框被 NMS 滤掉了(这些其实是定位优质的框,但却被滤掉了),这会严重损害最终的定位效果。 IoU-Net 的实现过程: 优势:对分类得分和定位得分解耦,避免了两者不对齐的问题,提升了效果 FCOS 是单阶段检测器,在只有分类和回归 loss 时,和两阶段检测器效果还有一定的差距,主要原因在于预测产生了很多距离目标中心点很远的低质量 bbox。 所以作者就提出了 centerness 分支,来预测每个预测框和真实框的 centerness 特征,即预测框和真实目标中心点的位置。 centerness 如何在 NMS 中使用:在测试时,和分类得分相乘,然后对框进行排序,距离越远的框得分会被很大程度地抑制下去,可以看做 centerness-NMS。 centerness 真值的计算公式如下: 极端情况下: 从 anchor-based 检测器的角度来看,anchor-based 方法使用两个 IoU 阈值来将 anchor 分为 negative、ignore、positive,centerness 可以被看做一个 soft threshold。 使用 centerness 参与 NMS 的效果分析: 单阶段目标检测器是将目标检测建模为了一个密集的分类和定位任务,分类使用 Focal loss,定位可以看做学习 Dirac 分布。 很多单阶段检测器由于没有预设的 anchor,导致定位效果较差,所有很多方法都引入了单独的预测分支来衡量定位的效果,如FCOS 中使用 centerness 来评估定位质量,然后在 NMS 排序时,将 centerness 和 分类 得分相乘,用于排序。 所以,主流单阶段检测方法有三个基础的元素: General Focal loss 其实是 Focal loss 的广义形式,下面的 QFL 和 DFL 也都是 GFL 的特殊形式: 主流算法问题 1:训练和测试不一致 ① 用法不一致: ② 对象不一致: 问题 1 解决方法:建立一个 classification-IoU joint representation 对于第一个训练和测试不一致的问题,为了保证训练和测试一致,同时还能兼顾分类和框质量预测都能训练到所有的正负样本,GFLv1 提出将框的表达和分类得分结合起来使用。 当预测的类别为 ground-truth 类别的时候,使用位置质量的 score 作为置信度,本文的位置质量得分就是使用 IoU 得分来衡量。 Quality Focal Loss(QFL): 主流算法问题 2:对框回归建模不够灵活,一般都使用狄拉克函数来建模,没办法建模复杂场景的不确定性 问题 2 解决方法:直接回归一个任意分布来建模框的表示 虽然人工标注可能会有一些误差,但人工标注边界的分布通常不会距离真正的边界位置太远,所以又在回归 loss(如 IoU、GIoU)的基础上额外增加了一个 DF Loss,一起来监督回归的效果,让网络快速的聚焦于标注位置附近。 Generalized Focal Loss 的形式: QFL 和 DFL 可以统一表示为 GFL: GFL 在训练的时候如何使用, loss 如下: 为什么 IoU-branch 比 centerness-branch 效果更好? centerness 是 FCOS 中提出的用于衡量预测框中心点和 gt 框中心点距离的指标,GFLv1 中 的 预测 IoU 是对预测框定位质量的预测,上面的实验证明了 IoU 效果更好一些,这是为什么呢? 本文作者通过分析后发现,主要原因在于对于极小的物体,centerness 的 label 非常小,难以被优化 为什么 label 小的时候难以被优化,或者说会降低网络的查全率呢,因为如果一些正样本的 centerness label 本来就很小,那么在 NMS 的时候,乘到 classification score 上,会拉低排序的得分,导致这些正样本被排到后面,就会漏检。 GFLv2 的结构(主要是比 V1 多了 DGQP 来衡量定位质量,V1 中使用的 IoU,其他的训练 loss 都是一样的): GFLV1 中提出的 generalized 分布,用于将位置分布建模为一个更通用的分布,且发现了边界模糊与否和位置分布的关系(越模糊,分布越平缓),但没有好好用这个分布。GFLV2 使用了这个分布的统计信息,来提取位置得分,指导模型训练。 GFLV 1 的 NMS 排序方式: GFLV1 是使用了 classification-IoU 的联合表达方式,来缓解训练和测试的不一致性,方式如下,当预测类别是真实类别时,联合表示特征 J = I o U J=IoU J=IoU,否则为 0。V1 这种方式虽然进行了联合使用,但还是有局限性的 GFLV2 在训练中对分类分支的监督和测试中 NMS 排序使用的都是 J J J: V2 同时使用分类得分(C)和由 Distribution-Guided Quality Predictor (DGQP) 得到的位置质量得分(I)作为联合表达,且同时用于训练和测试,不会有不一致性。 J = C × I J=C \times I J=C×I DGQP 的原理: DGQP-NMS 的优势: 详细介绍见 本文 现有的数据增强的方法一般可以分为如下三个类别,前两类主要是让训练数据更好的适应真实世界的情况,最后一种是人为的丢弃一些特征,目标遮挡、覆盖等难处理的情况: 代码大都可以在这里找到:https://github.com/open-mmlab/mmdetection/blob/master/mmdet/datasets/pipelines/transforms.py 目前几个用的比较多的方法: 动机: Cutout 具体做法: Cutout 的优点: 该方法通过随机选择一个随机大小的矩形区域,并给该区域赋予随机数值来实现。以此来模拟目标被遮挡的场景,比 cutout 的相同大小的抠图更灵活多变,且模拟引入了噪声。 方法 动机:现有的数据增强方法,大都是在单个图像内部进行丢弃,没有多个图像之间的融合。 方法:对 batch 中的所有图像,两两进行加权加和,进行类间-类内的图像混合,为网络引入了更多不确定因素 在 mini-batch 内部: 动机:虽然 CNN 会过拟合,但总的来说还是 data-angry 的,也就行需要更丰富的数据,别的方法擦除某些区域但也让网络接收的信息更少了,所以能不能在擦除的同时,用别的特征补上去呢? 方法:CutMix 可以看做 cutout 的优化,也就是擦除图像中的某个随机区域,然后使用同 batch 中的其他图像的区域来填补上去,真值 label 也同样被 mixed。 CutMix 的过程如下面公式所示: Mosaic 数据增强是在 YOLOv4 中提出来的,其实也是基于 Cutmix 的一个改进版本,能同时引入 4 个图像的信息。将 4 个训练图像进行混合,引入 4 种不同的上下文信息(CutMix 是混合 2 个图像),让网络能得到更多额外的上下文信息,而且,BN 也在每层接受了来自 4 个图像的信息,能够降低 “大 batch size” 的需求。 操作: 优势: 大大丰富了检测数据集,特别是随机缩放增加了很多小目标,让网络的鲁棒性更好 论文:Simple Copy-Paste is a Strong Data Augmentation Method for Instance Segmentation 出处:CVPR20221(Oral) 1、动机 如前所述,神经网络是 data-hungry 的,但人工标注费时费力,且之前的 cutmix、mosaic 等方法,难以适用于实例分割,Copy-paste 能够使用简单的方法,将实例扣下来并粘贴到别的图像上,很方便的解决了实例分割(也可用于有实力分割标签的目标检测)的数据增强问题。 2、方法 处理后的图像是什么样子的?说实话和真实场景的图像也很不一样,如图 2 所示,长颈鹿和人出现在一张图里了,而且尺度和平常的有很大不同。 论文:GridMask Data Augmentation 1、动机 Grid-mask 方法和 cutout、HaS 等方法类似,都是通过丢弃一部分图像信息来让网络更加鲁棒。但是作者认为移除的图像大小难以把控,移除过多会导致信息丢弃过多,保存的部分可能不足以支撑后续任务,移除过少会使得网络不够鲁棒,所以移除信息的多少难以把控。 Cutout 和 random erasing 方法,都是随机移除图中的某一个小块,有很大的随机性,如果移除的好则效果好,如果移除的效果不好,则会影响模型效果。 HaS 将图像切分为几个小块,然后随机移除其中的多个小块,但仍可能出现某些地方移除过多,有些地方移除过少的情况。 所以作者提出了均匀移除图像块的方法:Grid-mask 2、方法 1、动机 Information drop 方法中,如何平衡丢弃部分和保留部分是很重要的,尤其是在复杂的真实场景,目标的大小是不确定的,随机的生成丢弃区域可能会导致重要信息丢失,误导模型。 所以作者提出了一个有规律且稀疏的数据增强方法——fence-mask,虽然打破了图像中像素的连续性,但是可以接受的。 图 2 展示了细粒度的图像分类中,不同目标的差别很小,如果把这些主要差别丢失了,则会严重影响结果。 Neck是目标检测框架中承上启下的关键环节。它对Backbone提取到的重要特征,进行再加工及合理利用,有利于下一步head的具体任务学习,如分类、回归、keypoint、instance mask等常见的任务。 大体上分为六种,这些方法当然可以同时属于多个类别。 卷积网络中,深层特征包含更多的语义信息,浅层特征包含更多的细节信息。所以为了实现更好的信息融合,就有了 Feature Pyramid Network。backbone 是自底向上的特征抽取,FPN 特征融合是自顶向下的特征融合,将高层的语义特征传递给低层的细节特征, 高层网络虽然能响应语义特征,但是由于Feature Map的尺寸太小,拥有的几何信息并不多,不利于目标的检测;浅层网络虽然包含比较多的几何信息,但是图像的语义特征并不多,不利于图像的分类。这个问题在小目标检测中更为突出。 FPN 自顶向下的融合方式如下图: 高层的特征包含全局特征,低层的特征包含细节定位特征,所以 FPN 中的自顶向下的信息传输方式能够给低层特征引入全局信息,利于分类能力的提升。 PANet 认为如果使用从下到上的传输路径,则能够将底层的细节定位纹理信息传递到高层,所以,其建立了两个个非常“干净”的旁侧路径: PANet 具体是怎么强化自己的特征传输的? 以使用 ResNet 为例,并且使用 FPN 输出的 P 2 P_2 P2 到 P 5 P_5 P5 层特征,PANet 在 FPN 的后面(图 1 中展示为右侧)增加了一个特征路径: PANet 做了什么(前两点也适用于目标检测): NAS-FPN 是搜索出最适合的 FPN 结构,如下图就是为 RetinaNet 搜索出一个合适的结构: FPN、PANet、NAS-FPN 的跨尺度特征融合,都使用的相加,BiFPN 认为这些特征是来自不同分辨率的,对输出的贡献应该是不同的。所以 BiFPN 使用可学习的权重来学习不同特征图的重要程度,来进行加权。此外,不仅仅 backbone 对模型的缩放重要,预测网络头也同样重要。 EfficientDet 的最终结构如下: 论文:Going deeper with convolutions 出处:ILSVRC14 比赛的检测和分类任务的 SOTA 方法 Inception 的初始结构如下: 由于 3x3 或 5x5 卷积核非常耗费计算资源,所以经过通道降维的改进后的 Inception 模型如下: 其中有4个分支: 第一个分支对输入进行1x1的卷积,这其实也是 NIN 中提出的一个重要结构。1x1 的卷积是一个非常优秀的结构,它可以跨通道组织信息,提高网络的表达能力,同时可以对输出通道升维和降维。Inception Module的4个分支都用到了1x1的卷积,来进行低成本(计算量比3x3小很多)的跨通道的特征变换 第二个分支,先使用了 1x1 卷积,然后连接 3x3 卷积,相当于进行了两次特征变换 第三个分支,先使用 1x1 卷积,然后连接 5x5 卷积 第四个分支,3x3 最大池化后直接使用 1x1 卷积 在后续的优化中,逐步使用了 BN ,或者把 nxn 卷积核改成 1xn 和 nx1 的叠加,来降低计算量 论文: Deep residual learning for image recognition 出处:CVPR 2016 ResNet 在 2015 年被提出,在 ImageNet 比赛 classification 任务上获得第一名,因为它 “简单与实用” 并存,之后很多方法都建立在 ResNet50 或者 ResNet101 的基础上完成的,检测,分割,识别等领域都纷纷使用 ResNet,所以可见ResNet确实很好用。 ResNet 的结构设计: 这两种结构分别针对 ResNet34(左)和ResNet50/101/152(右),一般称整个结构为一个 “building block”,其中右图为“bottleneck design”,目的就是为了降低参数数目,第一个 1x1 的卷积把 256 维的 channel 降到 64 维,然后在最后通过 1x1 卷积恢复,整体上用到参数数目 69632,而不使用 bottleneck 的话就是两个 3x3x256 的卷积,参数数目: 3x3x256x256x2 = 1179648,差了16.94倍。 对于常规ResNet,可以用于34层或者更少的网络中,对于 Bottleneck Design 的 ResNet 通常用于更深的如 101 这样的网络中,目的是减少计算和参数量。 详细介绍见 本文 论文:Aggregated Residual Transformations for Deep Neural Networks 代码:https://github.com/miraclewkf/ResNeXt-PyTorch 出处:CVPR 2017 贡献: ResNeXt 是怎么做的: ResNeXt 提出了一个新的概念——cardinality,the size of the set of transformations,和网络深度以及宽度一起作为网络的设计量。 cardinality 也可以翻译为“基”或者“势”,表示一个 block 中,可以理解为特征被分为了几个基本单元,或者几组,如果被分为 32 组,则cardinality = 32。 ResNeXt 的设计也是重复的堆叠,且设计遵循两个规则,设计的结构如表 1 所示: ResNeXt 的结构和下面两个结构是很类似的: ① Inception-ResNet 如图 1 右侧所示的结构(也就是下图 3a),其实和图 3b 的结构是等价的,只是和 Inception-ResNet 不同的是,ResNeXt 的并行通道的卷积核大小是相同的,在设计上更简单通用。 ② Grouped Convolutions 如图 3c 所示,如果将图 3b 的第一层多个 1x1 卷积聚合起来,输出 128-d 特征向量,然后使用分组卷积(32组)来进行后续的特征提取,其实和图 3b 的并行分支是等价的,最后将分组卷积的每组卷积的输出 concat,就得到最后的输出。 详细介绍见 本文 论文:Densely Connected Convolutional Networks 代码:https://github.com/liuzhuang13/DenseNet 出处:CVPR2017 | 康奈尔大学 清华大学 Facebook 越来越深的神经网络会带来梯度消失问题,ResNet 和 Highway Network 使用了恒等映射的方式,让网络都超过了 100 层且效果良好,也就是给梯度增加了一条高速路,可以顺畅的在浅层和深层之间传输。 但这些传输只能在前后两层之间传递,没有最大化信息传输,所以作者提出了 DenseNet。 DenseNet 挣脱了加深和加宽模型的思路,而是通过最大限度的特征重用和旁路的思想来提升网络效果。 DenseNet 的动机:让信息在网络中的所有层中传递最大化 DenseNet 的做法:在一个 block 内部(即特征图大小都相同),将所有的层都进行连接,即第一层的特征会直接传输给后面的所有层,后面的层会接受前面所有层的输出特征。如图 1 所示。 DenseNet 的特征是如何结合的:不像 ResNet 那样相加起来,而是 concat,所以越往后通道越多 DenseNet 的参数少的原因:DenseNet 的通道很少(如每层 12 个通道),且层浅 下图展示了一个 Dense block 内部的结构,一个 block 内部会有多个卷积层,每个卷积层的输入来自前面所有层的输出,前面所有层的特征输出会 concat 然后送入当前层。 Dense 连接只会在每个 Dense block 内部进行,不会进行跨 block 的 Dense 连接 首先看一下 ResNet 的网络结构:每层接收上一层的特征输出和上一层的原始输出 然后再来看 DenseNet 的网络结构:每层接收前面所有层的特征输出,然后进行对应层的特征提取 DenseNet 的优点: 详细介绍见 本文 论文:CSPNet: A new backbone that can enhance learning capability of CNN 代码:https://github.com/open-mmlab/mmdetection/blob/master/mmdet/models/backbones/csp_darknet.py 出处:CVPR2019 CSPNet 的提出解决了什么问题: Cross Stage Partial Network (CSPNet) 的主要设计思想:让网络中的梯度进行丰富的结合,降低冗余,减少计算量 在介绍 CSPNet 之前,先看看 DenseNet 的结构 图 2a 展示了 DenseNet 的一个 stage 结构:每一层的输入来自于前面所有层输出的 concat 结果 DenseNet 的过程可以用如下方式表示,其中 * 表示卷积, x i x_i xi 表示第 i i i 个 dense layer 的输出。 反向传播过程表示如下, g i g_i gi 表示传递给第 i 个 dense layer的梯度。可以看出,大量的梯度信息是被不同 dense layer 重复使用的: 图 2b 展示了 CSPDenseNet 的一个 stage,CSPDenseNet 的组成: 由于这里 transition layer 使用的是 concat 方法,而 concat 方法的梯度传播会分开进行,就是还是会传递到对应的来源处去,所以经过密集 block 和未经过密集 block 的特征是分别优化的,梯度单独更新。 CSPDenseNet 保留了 DenseNet 特性重用特性的优点,但同时通过截断梯度流防止了过多的重复梯度信息。该思想通过设计一种分层的特征融合策略来实现,并应用于局部过渡层。 下图 3 也展示了不同时间进行特征融合的方式: 使用 Fusion First 中梯度会被大量重复利用,没有明显的计算量下降, top-1 acc 下降了 1.5% 使用 Fusion Last 先使用 transition 降低了 dense block 的维度,极大降低了计算量,top-1 acc 仅仅下降了0.1个百分点 同时使用 Fusion First 和 Fusion Last 相结合的 CSP 所采用的融合方式可以在降低计算代价的同时,提升准确率(图 3b) 将 CSPNet 和其他结构结合,如图 5 所示,CSPNet 可以和 ResNet、ResNeXt 进行结合,由于每个 Res block 只有一半的 channel 会经过,所以不需要引入 bottleneck。 详细介绍见 本文 论文:RepVGG: Making VGG-style ConvNets Great Again 代码:https://github.com/megvii-model/RepVGG 出处:CVPR2021 | 清华大学 旷世 RepVGG 的贡献: 随着 Inception、ResNet、DenseNet 等方法的提出,卷积神经网络越来越复杂,还有一些基于自动或手动框架选择,虽然这些复杂的网络能够带来好的效果,但仍然会有很多问题: 所以本文提出了 RepVGG,是一个 VGG-style 的结构,有如下优势: RepVGG 面临的问题: RepVGG 如何解决上述问题:结构重参数化(训练和推理使用不同的结构) RepVGG 的设计过程: 1、使用简单结构的卷积神经网络,更加灵活(ResNet 使用残差就限制了必须等大,且多分支结构难以通道剪枝) 2、在训练的时候使用多分支结构(ResNet 证明了多分支结构的效果):虽然多分支的结构在推理的时候效率严重不足,但其胜在训练的效果,所以 RepVGG 在训练的时候选择了多分支结构,而且选择的是 3 分支结构(1 个主分支,1 个 1x1 分支,1 个恒等映射分支, y = x + g ( x ) + f ( x ) y = x + g(x) + f(x) y=x+g(x)+f(x)),当有 n 个 blocks 时,相当于有 3 n 3^n 3n 个模型 3、在推理阶段进行重参数化:卷积有可加性,将每个 BN 和其前面的 conv 可以转换成一个【conv with bias vector】,然后将得到的 3 组卷积相加 RepVGG 结构: 表 2 展示了 RepVGG 的设计细节,包括宽度和深度,其中主要使用了 3x3 conv,没有使用 max pooling。 深度: 宽度: 详细介绍见 本文 论文:MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications 出处:CVPR 2017 | 谷歌 贡献: 更强的卷积神经网络一般情况下意味着更深和更宽的网络结构,但这样就会导致速度和效率的缺失,所以,MobileNet 的作者提出了一个搞笑的网络结构,致力于建立一个适用于移动端和嵌入式设备的网络结构。MobileNetV1 可以理解为把 VGG 中的标准卷积层换成深度可分离卷积 深度可分离卷积是 MobileNet 的一个非常重要的核心点,由两部分构成: 普通卷积是计算量: 深度可分离卷积的计算量: 故使用深度可分离卷积的计算量和普通卷积的计算量之比如下: D K ⋅ D K ⋅ M ⋅ D F ⋅ D F + M ⋅ N ⋅ D F ⋅ D F D K ⋅ D K ⋅ M ⋅ N ⋅ D F ⋅ D F = 1 N + 1 D K 2 \frac{D_K \cdot D_K \cdot M \cdot D_F \cdot D_F + M \cdot N \cdot D_F \cdot D_F}{D_K \cdot D_K \cdot M \cdot N \cdot D_F \cdot D_F} = \frac{1}{N} + \frac{1}{D_K^2} DK⋅DK⋅M⋅N⋅DF⋅DFDK⋅DK⋅M⋅DF⋅DF+M⋅N⋅DF⋅DF=N1+DK21 MobileNetV1 网络结构: 论文:MobileNetV2: Inverted Residuals and Linear Bottlenecks 出处:CVPR 2018 | 谷歌 贡献: 深度可分离卷积: V2 依然使用的深度可分离卷积,深度可分离卷积相比普通卷积大约能够降低 k 2 k^2 k2 的计算量,V2 的卷积核为 3x3,所以大约比普通卷积计算量少 8~9 倍,准确率仅仅跌了很少。 线性瓶颈: 线性瓶颈结构,就是末层卷积使用线性激活的瓶颈结构(将 ReLU 函数替换为线性函数),因为 ReLU 激活函数对低维信息会造成很大损失 模型框架: 论文:Searching for MobileNetV3 出处:ICCV 2019 | 谷歌 贡献: MobileNetV3 提出的目标就是为了实现移动设备上的模型的准确率和耗时的平衡。 MobileNetV1 引入了深度可分离卷积,来代替传统卷积 MobileNetV2 引入了线性瓶颈和反残差结构,来提升速度 MobileNetV3 为了 NAS 来搜寻更合适的网络,并且引入了 Swish 非线性方法的优化版本 h-swish 和 SE 模块,建立更高效的网络 NAS:这里使用 NAS 的目的是搜寻到更适合移动设备平台的 block 结构 网络优化: 1、重新设计计算复杂的层 NAS 得到搜寻的结构后发现,前面几层和后面几层计算复杂度很高,做了一些修整: 2、非线性激活的改进 swish 的形式如下: 使用 swish 的有个问题,sigmoid 函数计算量很大,所以 V3 从以下两个方面解决: 3、引入 SE 模块 在 V3 中使用 SE 模块,因为SE结构会消耗一定的时间,所以作者在含有 SE 的结构中,将 expansion layer 的 channel 变为原来的 1/4,这样作者发现,即提高了精度,同时还没有增加时间消耗。并且SE结构放在了depthwise 之后。实质为引入了一个 channel 级别的注意力机制。 4、不同大小的模型设计 V3 设计了两种体量的模型,Large 和 Small,都是经过 NAS 和优化后的。 详细介绍见 本文 论文:ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices 出处:CVPR 2018 | 旷世 现有的表现良好的网络结构动辄上百层,上千个通道,FLOPs(浮点计算次数)大概在十亿次,ShuffleNet 的提出是为了适应于算力较弱的移动端,以实现大概几十到几百的 MFLOPs 为目标。 现有网络的问题: 现有的高效结构如 Xception 和 ResNeXt,其实在极小的网络上的计算效率依然不太高,主要在于很耗费计算量的 1x1 卷积。 ShuffleNet 如何解决:使用 point-wise 分组卷积和 channel shuffle 两个操作,很好的降低计算量并保持准确率。这种结构能够允许网络使用更多的通道,帮助 encode 阶段提取更多的信息,这点对极小的网络非常关键。 这里再介绍几个基本概念: ShuffleNetV1 是怎么做的: 1、Channel shuffle for group convolutions Xception 使用了深度可分离卷积, ResNeXt 使用了分组卷积,但都没有考虑 1x1 的瓶颈层,该瓶颈层也会带来很大的计算量。 ResNeXt 中在分组卷积中使用的卷积大小为 3x3,对每个残差单元,逐点的卷积占了 93.4%。在极小的网络中,这样大的占比就难以降低网络计算量的同时来提升效果了。 为了解决上面 1x1 瓶颈层的问题,要怎么做呢: 2、ShuffleNet unit 作者又针对小网络提出了 ShuffleNet unit: 从如图 2a 的 bottleneck 单元开始,在 bottleneck 特征图上,使用 3x3 深度卷积,然后使用 point-wise group convolution + channel shuffle,来构成 ShuffleNet unit,如图 2b 所示 3、网络结构 ShuffleNet 结构如图 1 所示,是一个由 ShuffleNet units grouped 堆叠起来的 3 stage 网络,在每个 stage 的开头,stride = 2。 论文:ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design 出处:ECCV 2018 | 旷世 清华 贡献: 基础概念: FLOPS:每秒浮点计算数量 FLOPs:浮点计算数量 MAC:Memory Access Cost,内存访问成本,MAC 描述了这个复杂的网络到底需要多少参数才能定义它,即存储该模型所需的存储空间 目前卷积神经网络的设计大都依据计算量,也就是 FLOPs,浮点计算次数,但 FLOPs 不是一个直接的衡量方式,是一个大概的预估,而且也可能和我们更关系的直接衡量方法(如速度和时间)得到的结果不等,且实际模型的的速度等还依赖于内存消耗、硬件平台等,所以 ShuffleNetV2 会在不同的硬件平台上更直接的来评估,而非只依靠 FLOPs。 如图 1 所示,MobileNet v2 是 NASNET-A 快很多,但 FLOPs 却基本没差别,也证明了有相同 FLOPs 的模型可能速度有很大的不同,所以,只使用 FLOPs 作为衡量指标不是最优的。 FLOPs 和 speed 之间的不对等可能有以下两个原因: 如下图 2 所示,FLOPs 主要衡量卷积部分,虽然这一部分可能很耗时,但其他的如 data shuffle、element-wise operation(AddTensor、ReLU)等等也同样很耗费时间,所以 FLOPs 不应该作为唯一的衡量指标。 基于上面的分析,作者认为一个方法高效与否应该从下面两个方面来衡量: ShuffleNetV2 首先提出了 4 条设计高效网络的方法: 1、G1:输入输出通道相同的时候,MAC 最小,模型最快 很多网络都使用了深度可分离卷积,但其中的逐点卷积(1x1 卷积)计算量很大,1x1 卷积的计算量和其输入通道数 c 1 c_1 c1 和输出通道数 c 2 c_2 c2 有很大的关系,1x1 卷积的 FLOPs = h w c 1 c 2 hwc_1c_2 hwc1c2 假设内存很大,则内存消耗 MAC = h w ( c 1 + c 2 ) + c 1 c 2 hw(c_1+c_2)+c_1c_2 hw(c1+c2)+c1c2,和输入输出通道数相关性非常大,也有 M A C > = 2 ( h w B ) + B h w MAC >= 2 \sqrt(hwB) + \frac{B}{hw} MAC>=2(hwB)+hwB, MAC 的下线是由 FLOPs 决定的,当 1x1 卷积的输入输出通道数量相同的时候,MAC 最小。 如表 1,当固定 FLOPs 时,输入输出通道相同的时候,MAC 最小,模型最快。 2、G2:当分组卷积的分组数增大时(保持FLOPs不变时),MAC 也会增大,所以建议针对不同的硬件和需求,更好的设计对应的分组数,而非盲目的增加 1x1 分组卷积的 MAC 和 FLOPs 如下: 3、G3:网络设计的碎片化程度越高(或者说并行的分支数量越多),速度越慢(Appendix Fig 1) 如表 3 所示,4 分支并行的网络约比单分支的网络慢 3x 4、G4:不要过多的使用逐点运算 如图 2,点乘操作会耗费很长时间,点乘会出现在 ReLU、AddTensor、AddBias 等操作中,虽然 FLOPs 很低,但 MAC 很高。深度可分离卷积也有点乘操作,所以也有高的 MAC/FLOPs ratio。 比如使用 ResNet 中的 bottleneck (1x1 + 3x3 + 1x1,ReLU,shortcut)做实验,将 ReLU 和 shortcut 去掉后,提升了 20% 的速度。 所以基于上述准则,设计高效网络要遵循如下准则: ShuffleNet V2 的结构: 介绍 V2 的结构之前,先看看 V1 的设计问题: pointwise 分组卷积和 bottleneck 结构会提升 MAC(G1 和 G2),其计算消耗是不可忽略的,尤其是小模型。 使用大的分组数会不符合 G3 残差连接中的逐点相加操作也会带来大量计算,不符合 G4 所以,如果想要同时实现高容量和计算效率,关键问题是如何使用大量且等宽的 channel,而不是很多的分组 ShuffleNet V2 中提出了 Channel Split: 在 block 刚开始的时候,就将 channel 一分为二,如图 3c 为基本结构,下采样时候的结构如图 3d ShuffleNetV2 不仅仅高效,而且准确性也有保证,主要有两个原因: 详细介绍见 本文 论文:An Energy and GPU-Computation Efficient Backbone Network for Real-Time Object Detection 出处:CVPR 2019 Workshop 贡献: VoVNet 的目标是什么: 将 DenseNet 优化成一个更高效的网络,同时保留其在目标检测任务上的良好效果 VoVNet 和 DenseNet 的最主要的区别: ResNet 和 DenseNet 的不同在于特征聚合的方式: 这两种聚合方式有一些不同: DenseNet 的参数量和 FLOPs 也更低一些,原因在于,除了 FLOPs 之外,还有很多影响模型运行时间的因素: 高效网络设计的重要因素有如下两点: MAC:Memory Access Cost,内存访问成本,MAC 描述了这个复杂的网络到底需要多少参数才能定义它,即存储该模型所需的存储空间,每个卷积层的 MAC 可以计算如下: GPU 计算效率: 之所以一般要通过降低 FLOPs 的方法来加速的原因是,一般认为每个浮点运算的过程在相同设备上都是相同的。 但在 GPU 上却不是这样,因为 GPU 有并行加速策略,所以 GPU 呢给个同时处理多个浮点运算,这也是高效的一个很大的原因。 GPU 并行计算能力在计算大型 tensor 的时候很能体现出来,当把大的卷积核 split 后,GPU 并行的计算效率会变低,因为并行的部分变少了。 基于此,建立一个 layer 数量较少的网络可能会更好点 所以结论如下: 所以本文提出了一个新的概念:FLOPs per Second:FLOP/s,来衡量对 GPU 能力的利用情况,该值越大,则 GPU 的利用越高效 DenseNet 的 Dense Connection 的问题: 中间层的密集连接会必不可少的导致效率低下,因为随着层数的增加,输入 channel 数量也会线性增加。会有以下的问题: 只使用能相互互补(或相关性较小)的中间层特征,而非使用所有的中间层特征来生成最后的特征,会避免很多冗余 故此,作者认为,使用所有的中间层来进行密集连接其实带来的收益不多,所以,作者提出了一种新的密集链接方式:只使用每个 block 的最后一层进行特征聚合 One-shot Aggregation modules: OSA 模块就是只聚合每个 block 的最后一层特征,也就是在每个 block 的最后一层,对该 block 的前面所有层的特征进行 concat,只进行着一次的聚合。 该模块将中间层的特征聚合到最后一层。如图 1 所示。每个卷积层包含双向连接,一个连接到下一层以产生具有更大感受野的特征,而另一个仅聚合到最终输出特征映射。 OSA 能够提升 GPU 是计算效率,OSA 中间层的输入输出通道数相同,也不大需要使用 1x1 瓶颈层来降维,所以,OSA 层数更少、更高效 OSA 与 DenseNet 的不同之处总结如下: 信息量:用来衡量一个事件所包含的信息大小,一个事件发生的概率越大,则不确定性越小,信息量越小。公式如下,从公式中可以看出,信息量是概率的负对数: 熵:用来衡量一个系统的混乱程度,代表系统中信息量的总和,是信息量的期望,信息量总和越大,表明系统不确定性就越大。 E n t r o p y = − ∑ p l o g ( p ) Entropy = -\sum p log(p) Entropy=−∑plog(p) 交叉熵:用来衡量实际输出和期望输出的接近程度的量,交叉熵越小,两个概率分布就越接近。 pytorch中的交叉熵: Pytorch中CrossEntropyLoss()函数的主要是将softmax-log-NLLLoss合并到一块得到的结果。 交叉熵loss可以用到大多数语义分割场景中,但他有一个明显的缺点,对于只用分割前景和背景时,前景数量远远小于背景像素的数量,损失函数中y=0的成分就会占据主导,使得模型严重偏向背景,导致效果不好。 语义分割 cross entropy loss计算方式: 输入 model_output=[2, 19, 128, 256] # 19 代表输出类别 1、将model_output的维度上采样到 [512, 1024] 2、softmax处理:这个函数的输入是网络的输出预测图像,输出是在dim=1(19)上计算概率。输出维度不变,dim=1维度上的值变成了属于每个类别的概率值。 3、log处理: 4、nll_loss 函数(negative log likelihood loss):这个函数目的就是把标签图像的元素值,作为索引值,在temp3中选择相应的值,并求平均。 如果第一个点真值对应的3,则在预测结果中第3个通道去找该点的预测值,假设该点预测结果为-0.62,因为是loss前右负号,则最终结果变为0.62。其余结果依次类推,最后求均值即时最终损失结果。 L = ∑ c = 1 M w c y c l o g ( p c ) L = \sum_{c=1}^Mw_cy_clog(p_c) L=c=1∑Mwcyclog(pc) 这个参数 w c w_c wc计算公式为 w c = N − N c N w_c = \frac{N-N_c}{N} wc=NN−Nc,其中N表示总的像素格式, N c N_c Nc 表示GT类别为c的像素个数,相比原来的loss,在样本数量不均衡的情况下可以获得更好的效果。 在one-stage检测算法中,目标检测器通常会产生10k数量级的框,但只有极少数是正样本,会导致正负样本数量不平衡以及难易样本数量不平衡的情况,为了解决则以问题提出了focal loss。 Focal Loss是为one-stage的检测器的分类分支服务的,它支持0或者1这样的离散类别label。 目的是解决样本数量不平衡的情况: 一般分类时候通常使用交叉熵损失: C r o s s E n t r o p y ( p , y ) = { − l o g ( p ) , y = 1 − l o g ( 1 − p ) , y = 0 CrossEntropy(p,y)= \begin{cases} -log(p), & y=1 \\ -log(1-p), & y=0 \end{cases} CrossEntropy(p,y)={−log(p),−log(1−p),y=1y=0 为了解决正负样本数量不平衡的问题,我们经常在二元交叉熵损失前面加一个参数 α \alpha α。负样本出现的频次多,那么就降低负样本的权重,正样本数量少,就相对提高正样本的权重。因此可以通过设定 α \alpha α的值来控制正负样本对总的loss的共享权重。 α \alpha α取比较小的值来降低负样本(多的那类样本)的权重。即: C r o s s E n t r o p y ( p , y ) = { − α l o g ( p ) , y = 1 − ( 1 − α ) l o g ( 1 − p ) , y = 0 CrossEntropy(p,y)= \begin{cases} -\alpha log(p), & y=1 \\ -(1-\alpha) log(1-p), & y=0 \end{cases} CrossEntropy(p,y)={−αlog(p),−(1−α)log(1−p),y=1y=0 虽然平衡了正负样本的数量,但实际上,目标检测中大量的候选目标都是易分样本。这些样本的损失很低,但是由于数量极不平衡,易分样本的数量相对来讲太多,最终主导了总的损失。 因此,Focal loss 论文中认为易分样本(即,置信度高的样本)对模型的提升效果非常小,模型应该主要关注与那些难分样本 。一个简单的想法就是只要我们将高置信度样本的损失降低一些, 也即是下面的公式: 当 γ = 0 \gamma=0 γ=0 时,即为交叉熵损失函数,当其增加时,调整因子的影响也在增加,实验发现为2时效果最优。 假设取 γ = 2 \gamma=2 γ=2,如果某个目标置信得分p=0.9,即该样本学的非常好,那么这个样本的权重为 ( 1 − 0.9 ) 2 = 0.001 (1-0.9)^2=0.001 (1−0.9)2=0.001,损失贡献降低了1000倍。 为了同时平衡正负样本问题,Focal loss还结合了加权的交叉熵loss,所以两者结合后得到了最终的Focal loss: F o c a l l o s s = { − α ( 1 − p ) γ l o g ( p ) , y = 1 − ( 1 − α ) p γ l o g ( 1 − p ) , y = 0 Focal loss = \begin{cases} -\alpha (1-p)^\gamma log(p), & y=1 \\ -(1-\alpha) p^\gamma log(1-p), & y=0 \end{cases} Focalloss={−α(1−p)γlog(p),−(1−α)pγlog(1−p),y=1y=0 取 α = 0.25 \alpha=0.25 α=0.25 在文中,即正样本要比负样本占比小,这是因为负样本易分。 单单考虑alpha的话,alpha=0.75时是最优的。但是将gamma考虑进来后,因为已经降低了简单负样本的权重,gamma越大,越小的alpha结果越好。最后取的是alpha=0.25,gamma=2.0 https://zhuanlan.zhihu.com/p/49981234 Varifocal 论文中提出了一个概念 IACS:分类得分向量中的一个标量元素 为了学习 IACS 得分,作者设计了一个 Varifocal Loss,灵感得益于 Focal Loss。 Varifocal Loss: Focal loss 对正负样本的处理是对等的(也就是使用相同的参数来加权),而 Varifocla loss 是使用不对称参数来对正负样本进行加权。 Varifocal loss 是如何不对等的处理前景和背景对 loss 的贡献的呢:VFL 只对负样本进行了的衰减,这是由于正样本太少了,希望更充分利用正样本的监督信号 L 1 ( x ) = ∣ x ∣ L_1(x)=|x| L1(x)=∣x∣ Δ L 1 ( e ) Δ ( e ) = { 1 , x > = 0 − 1 , o t h e r w i s e \frac{\Delta L_1(e)}{\Delta(e)}= \begin{cases} 1, & x>=0 \\ -1, & otherwise \end{cases} Δ(e)ΔL1(e)={1,−1,x>=0otherwise L2 损失公式: L2损失的梯度: L2 loss 的缺点: L1 loss 和 L2 loss 的对比: 公式如下: s m o o t h L 1 ( x ) = { 0.5 x 2 , i f ∣ x ∣ < 1 ∣ x ∣ − 0.5 , o t h e r w i s e smooth_{L1}(x) = \begin{cases} 0.5x^2, & if |x|<1 \\ |x|-0.5, & otherwise \end{cases} smoothL1(x)={0.5x2,∣x∣−0.5,if∣x∣<1otherwise Smooth L1 Loss特点: smooth L1 loss 相对于 L2 loss的优点: 上面三种 Loss 用于计算目标检测的bounding-box loss时,独立的求出4个点的loss,然后进行相加得到最终的bounding-box loss。 论文:UnitBox: An Advanced Object Detection Network 出处:ACM MM 2016 IoU loss:L1 和 L2 loss是将bbox四个点分别求loss然后相加,并没有考虑靠坐标之间的相关性,而实际评价指标 IoU 是具备相关性。 有一些情况的 L1 loss一样,但实际上两个框的 IoU 有很大的不同,所以难以很好的衡量 anchor 的质量。 IoU loss 常用版本: L I o U = 1 − I o U L_{IoU} = 1-IoU LIoU=1−IoU 上图展示了L2 Loss和 IoU Loss 的求法,图中红点表示目标检测网络结构中Head部分上的点 ( i , j ) (i,j) (i,j),绿色的框表示GT框, 蓝色的框表示Prediction的框。 IoU loss的定义如上,先求出2个框的IoU,然后再求个 − l n ( I o U ) -ln(IoU) −ln(IoU),在实际使用中,实际很多IoU常常被定义为 I o U L o s s = 1 − I o U IoU Loss = 1-IoU IoULoss=1−IoU。 其中IoU是真实框和预测框的交集和并集之比,当它们完全重合时,IoU就是1,那么对于Loss来说,Loss是越小越好,说明他们重合度高,所以IoU Loss就可以简单表示为 1- IoU。 IoU Loss 的优点: IoU Loss 的缺点: 由于 IoU loss 无法反应两框如何相交,且无法优化未重叠框,则 GIoU Loss 被提出。 方法: 在 IoU 基础上加了一个惩罚项,当bbox的距离越大时,惩罚项将越大: GIoU 的优点: GIoU存在的问题: 论文:Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression 代码:https://github.com/Zzh-tju/DIoU 出处:AAAI2020 DIoU 损失: Distance-IoU 和 Complete-IoU 来自同一篇文章。 由于 GIoU 存在收敛较慢等问题,作者提出了新的损失函数。提出该损失函数的前提是,作为认为一个好的 loss 函数,需要同时考虑三个方面: 所以,Distance-IoU 在 IoU 的基础上添加了对两个框中心点距离的约束,从公式可以看出,D-IoU 能够同时最小化外接矩形的面积和两框中心点的距离,这会使得网络更倾向于移动 bbox 的位置来减少 loss: DIoU loss 的优点: DIoU 被用于 NMS 中,得到 DIoU-NMS,使用 DIoU 作为 NMS 中框排序的依据,同时考虑了重合率和中心点距离作为衡量指标。 对于有高得分的框 M,DIoU-NMS 被定义如下: CIoU 损失: 当两个框中心点重合的情况下,DIoU loss 无法继续优化,c 和 d 的值都不变,所以引入了框的宽高比。 Complete-IoU 在 IoU 的基础上同时考虑了对中心点距离和纵横比的约束,公式如下: 其中: Loss 函数定义如下: α \alpha α 定义如下, CIoU 的优化和 DIoU 一致,除过 v v v 要对 w w w 和 h h h 分别求导: CIoU 的优点(在 DIoU 优点的基础上): CIoU 的缺点: 虽然 CIoU 同时考虑了交并比、中心点距离和纵横比,但纵横比是对一个比例的优化,而非对单独参数的优化,导致 w 和 h 无法同大同小,必须一个变大,一个变小,这会限制模型的优化效果。所以 EIoU 将纵横比的优化改为了对 w 和 h 的单独优化,分别求两个框的 w 和 h 的差,用于模型优化。 EIoU Loss 定义如下: Focal-EIoU loss: 在框回归问题中,高质量的 anchor 总是比低质量的 anchor 少很多,这也对训练过程有害无利。所以,需要研究如何让高质量的 anchor 起到更大的作用。这里的高质量就是指的回归误差小的框。 下图中,经过实验, β = 0.8 \beta=0.8 β=0.8 效果最优, L F o c a l − E I o U = I o U γ L E I o U L_{Focal-EIoU}=IoU^{\gamma} L_{EIoU} LFocal−EIoU=IoUγLEIoU 这里以 IoU loss 的形式来分析一下 Focal 形式的曲线(EIoU 曲线不太好画),蓝线为 ( 1 − I o U ) (1-IoU) (1−IoU) 曲线,橘色线为 I o U 0.5 ( 1 − I o U ) IoU^{0.5}(1-IoU) IoU0.5(1−IoU),所以在 IoU 小的时候(0-0.8), I o U 0.5 ( 1 − I o U ) IoU^{0.5}(1-IoU) IoU0.5(1−IoU) 会被拉低,在 IoU 大的时候(0.8-1), I o U 0.5 ( 1 − I o U ) IoU^{0.5}(1-IoU) IoU0.5(1−IoU) 基本保持不变。 从这个曲线可以看出,Focal-EIoU loss 能够通过降低难样本的 loss 来让网络更关注简单样本。 作者认为,在检测任务中,IoU 经常被用来选择预选框,但这种直接的做法也忽略了样本分布的不均衡的特点,这会影响定位 loss 的梯度,从而影响最终的效果。 所以作者思考,能不能在训练的过程中不断 rectify 所有样本的梯度,来提升效果。于是就提出了 Rectified IoU (RIoU) loss。 该损失函数和 Focal-EIoU 类似,都是为了提高 high IoU 样本的权重,来让网络更关注简单样本,提升训练的稳定性,并且让不同难易程度的样本更平衡。 Rectified IoU (RIoU) loss 的目的:增大 high IoU 样本的梯度,抑制 low IoU 样本的梯度 Rectified IoU (RIoU) loss 的特点:在使用 RIoU 训练时,大量简单样本(IoU 大)的梯度会被增大,让网络更关注这些样本,而少量的难样本(IoU 小)的梯度会被抑制。这样会使得每种类型的样本的贡献更均衡,训练过程更高效和稳定。 为什么抑制难样本的梯度后,每类样本的贡献会更均衡呢? 因为 IoU 低的样本占大多数,所以对应的 loss 更大,所以作者通过提高简单样本对 loss 的贡献,来让难易样本的贡献更均衡。 L I o U L_{IoU} LIoU 的形式如下: L I o U = 1 − I o U L_{IoU}=1-IoU LIoU=1−IoU L I o U L_{IoU} LIoU 的偏导如下: ∣ g r a d i e n t s ( I o U ) ∣ = ∣ ∂ L I o U ∂ I o U ∣ = 1 |gradients(IoU)|=|\frac{\partial L_{IoU}}{\partial_{IoU}}|=1 ∣gradients(IoU)∣=∣∂IoU∂LIoU∣=1 由此可看出, ∣ g r a d i e n t s ( I o U ) ∣ |gradients(IoU)| ∣gradients(IoU)∣ 是一个常数,对难易样本无差别对待,但不同 IoU 样本的分布是很不均衡的。low IoU 样本的数量大于 high IoU 样本的数量,也就是说,在训练过程中,low IoU 样本掌握着梯度,让网络更偏向于难样本的回归。 Rectified IoU (RIoU) loss 的目的:增大 high IoU 样本的梯度,抑制 low IoU 样本的梯度 如何修正呢: 如果梯度总是随着 IoU 的增大而增大,则会面临一个问题,即当某个框回归的非常好时( I o U → 1 IoU \to 1 IoU→1),其梯度会最大,这是不合适的。 所以作者提出了如下的方式,a, b, c, k 可以控制梯度曲线的形状。上升后,在 I o U = β IoU =\beta IoU=β 处快速下降,本文 β = 0.95 \beta=0.95 β=0.95。 前面了 Focal-EIoU 和 R-IoU loss 都是通过提高 high IoU object 对 loss 的贡献,来平稳训练过程,提升训练效果,这两个方法主要是提高 high IoU object 的梯度,但这两者都不够简洁,并且没有进行全面的实验对比。 所以有研究者提出了一个对 IoU loss 的统一形式,通过 power transformation 来生成 IoU 和其对应惩罚项的统一形式,来动态调整不同 IoU 目标的 loss 和 gradient。 α \alpha α-IoU 的形式是怎样的: 首先,在 IoU loss L I o U = 1 − I o U L_{IoU} = 1-IoU LIoU=1−IoU 上使用 Box-Cox 变换,得到 α \alpha α-IoU: 对 α \alpha α 的分析如下,可以得到很多形式: 对 α \alpha α-IoU 简化得到: 图 1 左侧展示了 IoU 和 L I o U L_{IoU} LIoU 的关系,图 1 右侧展示了 IoU 和梯度模值的关系。 α > 1 \alpha>1 α>1,能够让网络更加关注 high IoU 的样本,且能够在训练后期提升训练效果,本文作者发现 α = 3 \alpha=3 α=3 对大多数情况表现都较好,所以选择了 α = 3 \alpha=3 α=3。 L α − I o U L_{\alpha-IoU} Lα−IoU 是如何动态调整的:
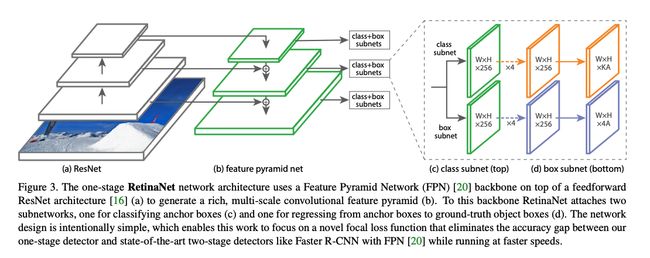
C r o s s _ E n t r o p y _ L o s s = 1 N ( ∑ 1 m l o g ( p ) − ∑ 1 n l o g ( 1 − p ) ) Cross\_Entropy\_Loss = \frac{1}{N} (\sum_1^m log(p) - \sum_1^n log(1-p)) Cross_Entropy_Loss=N1(1∑mlog(p)−1∑nlog(1−p))
F o c a l _ L o s s = { − ( 1 − p ) γ l o g ( p ) , y = 1 − p γ l o g ( 1 − p ) , y = 0 Focal\_Loss = \begin{cases} -(1-p)^ \gamma log(p), & y=1 \\ -p^\gamma log(1-p), & y=0 \end{cases} Focal_Loss={−(1−p)γlog(p),−pγlog(1−p),y=1y=0
1.2.4 CenterNet
1.2.5 FCOS
2、Label Assignment
2.1 RetinaNet
2.2 FCOS
2.3 ATSS
2.4 Free Anchor
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
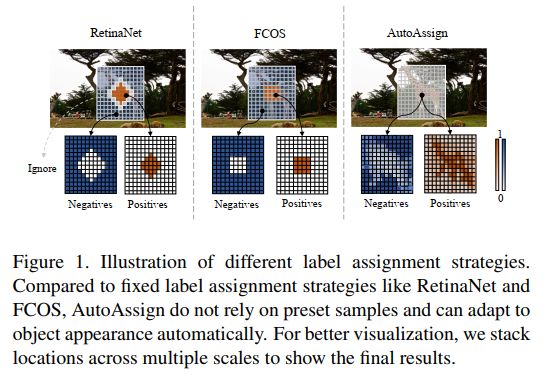
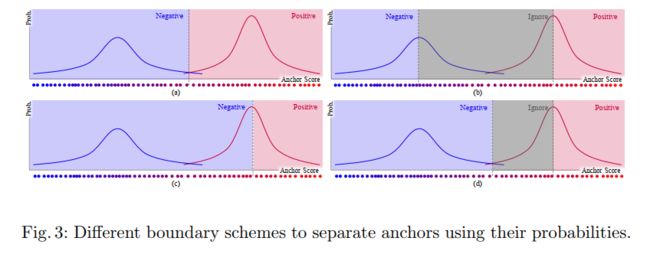
2.5 AutoAssign
2.6 PAA
![]()
2.7 OTA
![]()
2.8 SimOTA
![]()
3、后处理之 NMS
3.1 NMS
3.2 Soft NMS
3.3 Softer NMS
![]()
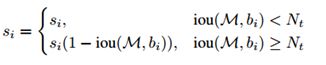
当相邻检测框与候选框重叠超过阈值 N t N_t Nt 时,得分线性衰减,但该函数并非线性函数,容易产生突变,所以需要找到一个连续的函数,对没有重叠的框的得分不衰减,对高度重叠的框进行较大的衰减,即高IoU的有高的惩罚,低IoU的有低的惩罚,且是逐渐过渡的,所以就有了第二种。
3.4 IoU-Net:IoU-Guided NMS
3.5 FCOS:Centerness-NMS
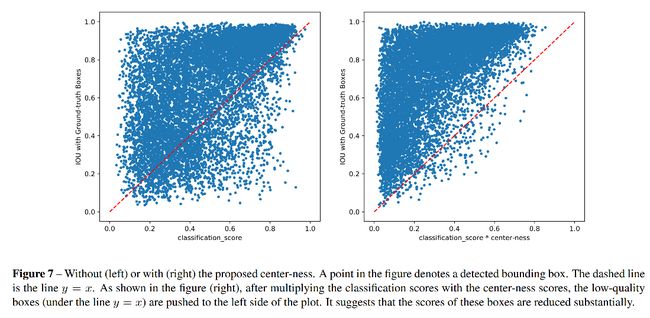
3.6 GFLV1:Classification-IoU-NMS
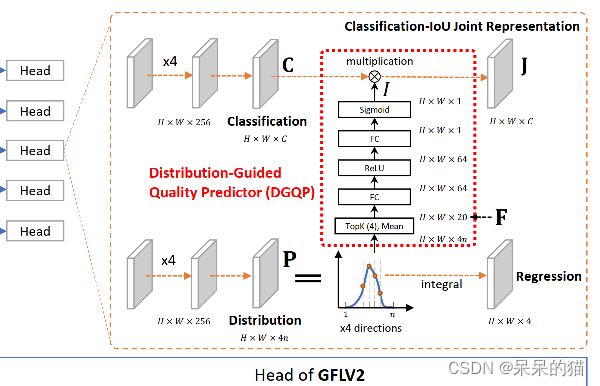
3.7 GFLV2:DGQP-NMS
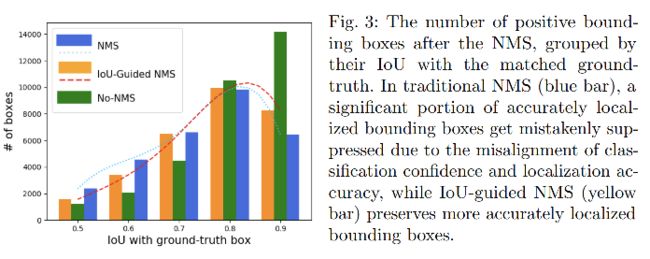
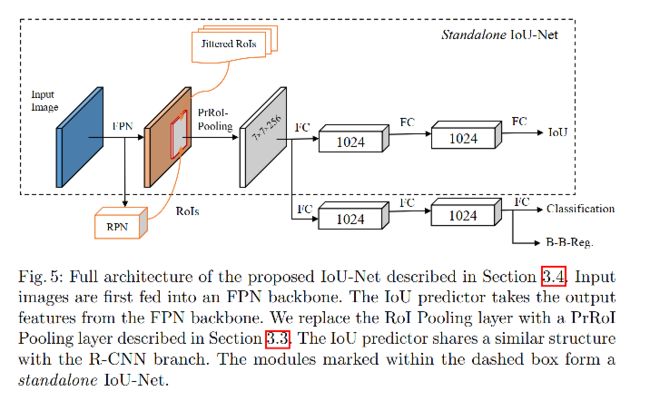
![]()
4、数据增强
4.1 Cutout
4.2 Random Erasing
4.3 Mixup
4.4 CutMix
4.5 Mosaic
4.6 Copy-paste
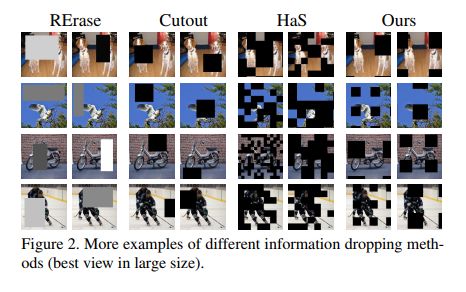
4.7 Grid-Mask
4.8 Fence-Mask
5、Neck
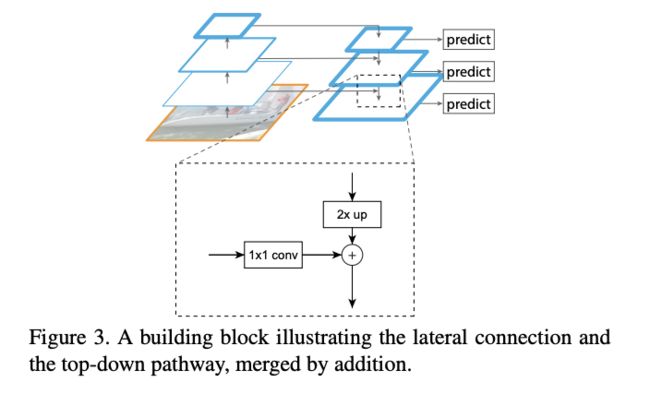
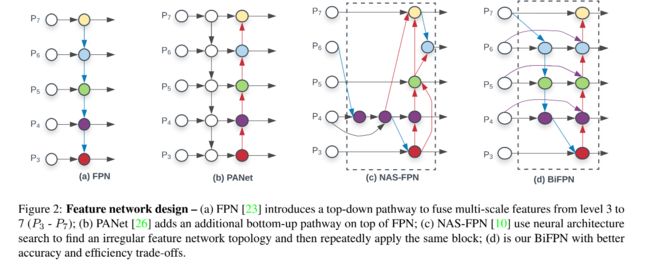
5.1 FPN
![]()
5.2 PAN
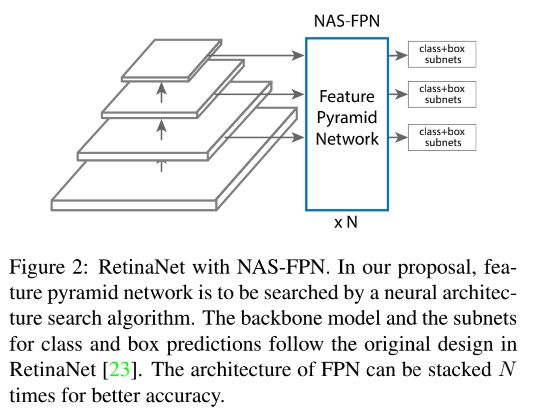
5.3 NAS-FPN
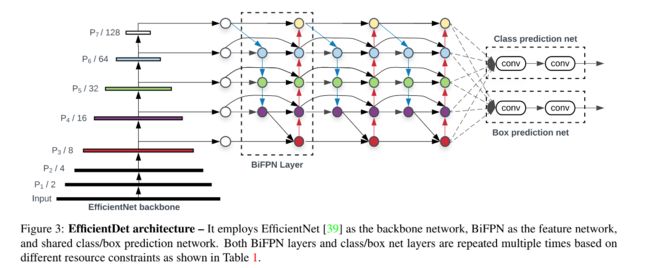
5.4 BiFPN
![]()
6、Backbone
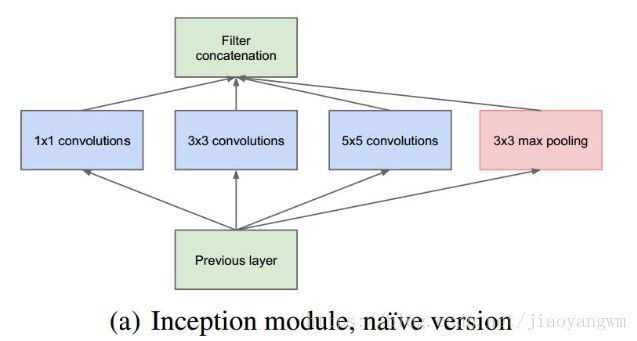
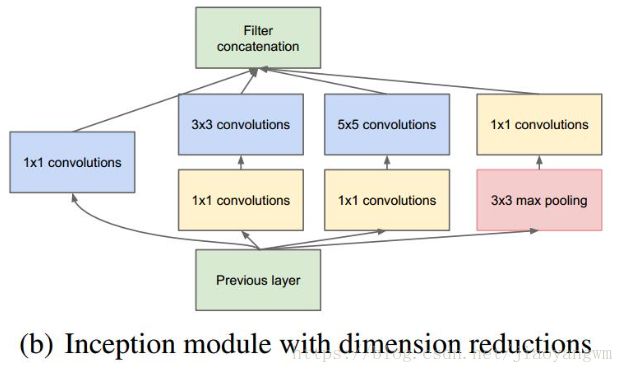
6.1 GoogLeNet
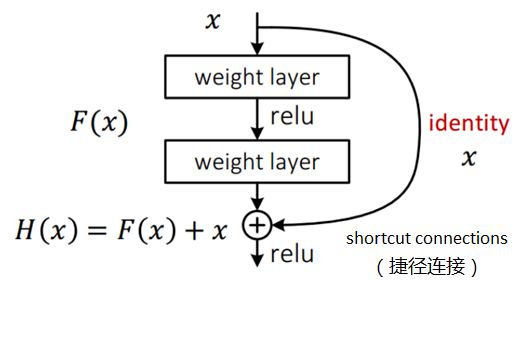
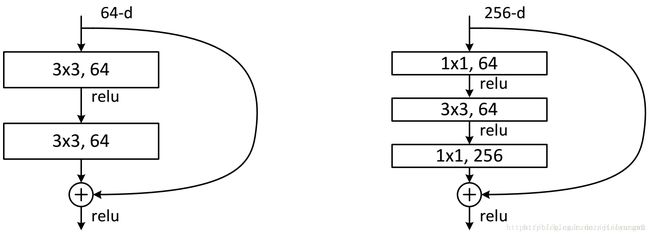
6.2 ResNet
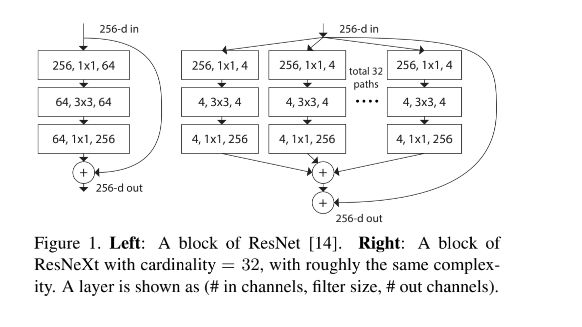
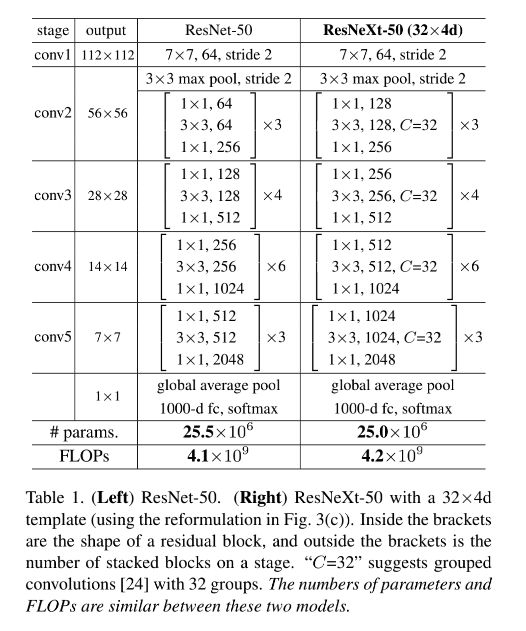
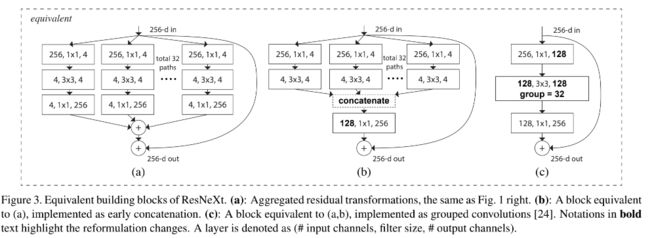
6.3 ResNeXt
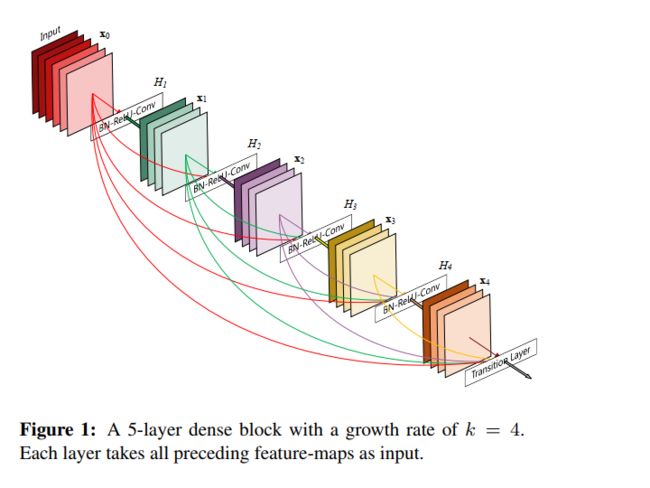
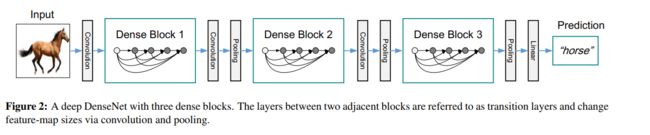
6.4 DenseNet
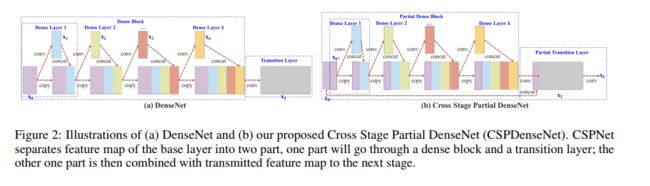
6.5 CSPNet
每个 stage 的特征图都根据 channel 被分为两个部分 x 0 = [ x 0 ′ , x 0 ′ ′ ] x_0 = [x_0', x_0''] x0=[x0′,x0′′]
6.6 RepVGG
6.7 MobileNet 系列
6.7.1 MobileNetV1
6.7.2 MobileNetV2
6.7.3 MobileNetV3
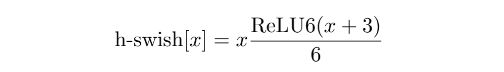
6.8 ShuffleNet 系列
6.8.1 ShuffleNetV1
6.8.2 ShuffleNetV2
6.9 VoVNet
![]()
7、Loss 函数
7.1 分类 loss 函数
7.1.1 CrossEntropy Loss
h ( x ) = − l o g 2 p ( x ) h(x) = -log_2p(x) h(x)=−log2p(x)
L = ∑ c = 1 M y c l o g ( p c ) L = \sum_{c=1}^My_clog(p_c) L=c=1∑Myclog(pc)
其中,M表示类别数, y c y_c yc是label,即one-hot向量, p c p_c pc是预测概率,当M=2时,就是二元交叉熵损失
标签 target=[2, 512,1024]x_softmax = F.softmax(x,dim=1)
log_softmax_output = torch.log(x_softmax)
output = nn.NLLLoss(log_softmax_output, target)
![]()
7.1.2 带权重的交叉熵Loss
7.1.3 Focal Loss
F o c a l l o s s = { − ( 1 − p ) γ l o g ( p ) , y = 1 − p γ l o g ( 1 − p ) , y = 0 Focalloss = \begin{cases} -(1-p)^ \gamma log(p), & y=1 \\ -p^\gamma log(1-p), & y=0 \end{cases} Focalloss={−(1−p)γlog(p),−pγlog(1−p),y=1y=0![]()
7.1.4 Varifocal loss
7.2 定位 loss 函数
7.2.1 L1 损失
L1损失的梯度:7.2.2 L2 损失
L 2 ( x ) = x 2 L_2(x)=x^2 L2(x)=x2
Δ L 2 ( e ) Δ ( e ) = 2 e \frac{\Delta L_2(e)}{\Delta(e)}=2e Δ(e)ΔL2(e)=2e
7.2.3 Smooth L1 损失
7.2.4 IoU 损失
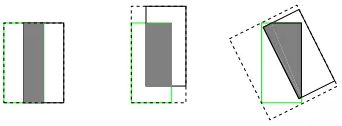
7.2.5 GIoU 损失
7.2.6 Distance-IoU 损失
![]()
因为 ∂ v ∂ w = − h w . ∂ v ∂ h \frac{\partial v}{\partial w} = - \frac{h}{w}.\frac{\partial v}{\partial h} ∂w∂v=−wh.∂h∂v,而偏导又是正值,所以有这样的关系。7.2.7 Foal-EIoU 损失

Focal-EIoU 要实现的目标:IoU 越高的高质量样本,损失越大,也就是回归越好的目标,给的损失的权重越大,相当于加权,让网络更关注那些回归好的目标,毕竟后面还要做 NMS,低质量的框可以给更少的关注。

所以 Focal-EIoU loss 公式如下, γ = 0.5 \gamma=0.5 γ=0.5 最优(图 9c):
7.2.8 R-IoU 损失

当 β = 0.95 \beta=0.95 β=0.95 时的 Loss 曲线对应如下, I o U < β IoU<\beta IoU<β 时是凸型, I o U > β IoU>\beta IoU>β 时是凹型:7.2.9 Alpha-IoU 损失
L α − I o U = ( 1 − I o U α ) α , α > 0 L_{\alpha-IoU}=\frac{(1-IoU^{\alpha})}{\alpha}, \alpha>0 Lα−IoU=α(1−IoUα),α>0