小波分析及相应MATLAB实现

参考：A Practical Guide to Wavelet Analysis
本文主要学习上述链接文章，并提出自己的一点思考和疑问。

小波分析（Wavelet Analysis）基本原理

1.Introduce

地球物理学中许多时间序列在统计上表现出非平稳性。虽然序列可能包含主导周期信号，但这些信号的振幅和频率可以在很长一段时间内变化。
一个例子是赤道太平洋的海表温度(图1)。变率的主导“模式”是El Niño-Southern振荡(ENSO)，在2-7年的时间尺度上显示为高频“尖峰”。叠加在这个信号上的是更长的年代际波动。年代际波动具有调节El Niño事件发生幅度和频率的作用。

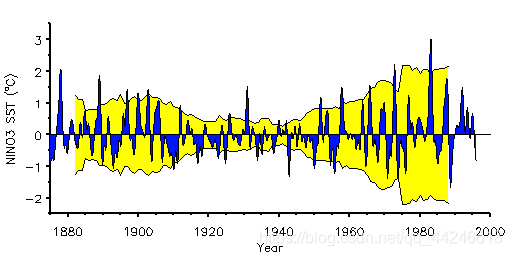
图1 东太平洋(5°S-5°N, 90°W-150°W) NINO3区域的海表平均温度较高。蓝色曲线为低通滤波(>12个月)的海表温度。黄色背景曲线是15年的方差，在15年周期的中间点。曲线被倒过来复制，以显示方差的“包络”

理想情况下，人们希望将较短周期的振荡与较长周期的振荡分开。
注:此处使用“振荡”一词来表示时间序列中任何重复的波动，无论这种波动是否有规律地重复。在我们的例子中，El Niño绝对是一个非周期(不规则)信号。

分析时间序列的非平稳性最简单的方法是计算统计数据，如不同时间段的均值和方差，看看它们是否有显著差异。

在图1中，我们还绘制了运行的15年方差，作为信号相对于时间的固有总功率的测量。我们可以看到，在1880-1920年和1950年之后，ENSO有更多的变化，在1920-1950年期间有一个相对平静的时期。
虽然运行方差告诉我们信号在特定时间的总体强度，但它存在两个主要缺陷:
【时间定位】曲线的形状高度依赖于所用窗口的长度。上面选择的15年是平滑度过高(比如使用30年窗期)和过低(5年窗期)之间的折衷。理想的方法是根据感兴趣的尺度允许不同的窗口大小。
【频率定位】运行方差不包含周期信号的频率信息，只包含它的振幅(并且只有当窗口被广泛选择时)。

一种可能是做一个窗口(或运行)傅里叶变换(WFT)，使用特定的窗口大小并在时间上滑动它，每次只使用窗口内的数据计算FFT。这将解决第二个问题(频率本地化)，但仍然取决于所使用的窗口大小。
WFT的主要问题是对不同频率的不一致处理:在低频时，窗口内的振荡太少，导致频率局部化丢失;而在高频时，振荡太多，导致时间局部化丢失。最后，WFT依赖于信号可以分解为正弦分量的假设。

小波分析试图通过同时将时间序列分解为时间/频率空间来解决这些问题。我们既可以得到级数中任何“周期”信号的振幅信息，也可以得到振幅随时间的变化情况。

2.Wavelets

在前一节中，我们看到了如何使用固定宽度窗口计算运行方差来衡量时间序列的平稳性。虽然我们指出了使用固定宽度窗口的缺点，但可以使用不同的窗口宽度重复分析。通过平滑地改变窗口宽度，我们就可以建立方差随时间和窗口宽度变化的图像。这种技术的明显问题是窗口函数的简单“车厢”形状，这引入了边缘效应，如振铃。正如前面提到的，使用这样一个黑匣子汽车，我们仍然不知道盒子里发生了什么，而只是恢复了平均能量。
在图2a中，我们看到了一个波“包”的例子，它具有有限的持续时间和特定的频率。你可以想象用这样一个形状作为我们方差分析的窗口函数。这种“小波”的优点是包含了一定周期的波，并且在范围上是有限的。事实上，图2a所示的小波(称为Morlet小波)只不过是一个正弦波(图2b中的绿色曲线)乘以一个高斯包络线(红色曲线)。
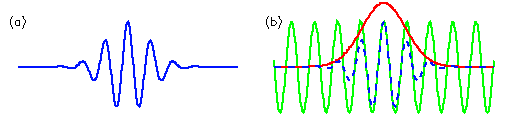图2 (a)沿x轴随时间变化的任意宽度和振幅的Morlet小波。(b)构造Morlet小波(蓝色虚线)作为正弦曲线(绿色)调制的高斯曲线(红色)。

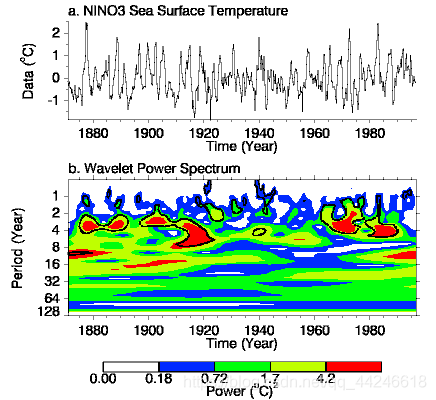
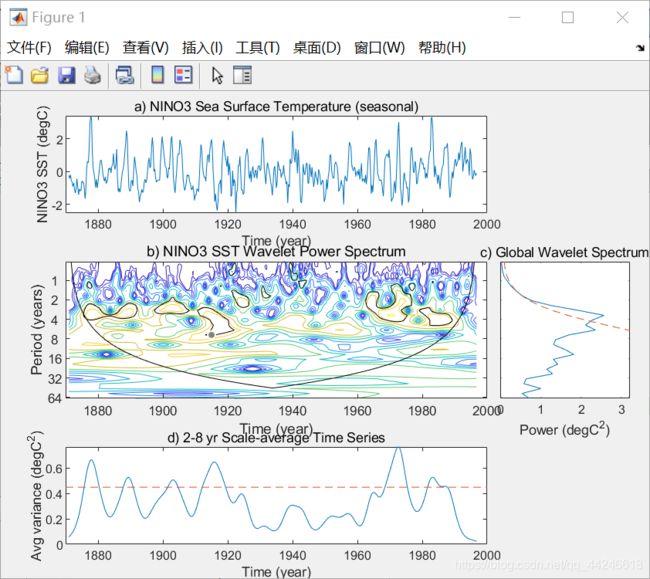
图3 (a) El Niño海表温度时间序列。(b)小波功率谱，使用Morlet小波。
x轴是小波在时间上的位置。y轴为以年为单位的小波周期。黑色轮廓是10%显著性区域，使用红色噪声背景光谱。红色区域表明，1880-1920年和1965-现在的高厄尔尼诺Niño活动发生，而1920-1960年则相对平静。

3.Algorithms

4.Monte Carlo

5.References

相关MATLAB代码

数据：Nino3 区海表温度（SST）序列，1870-1996共126年的季尺度数据

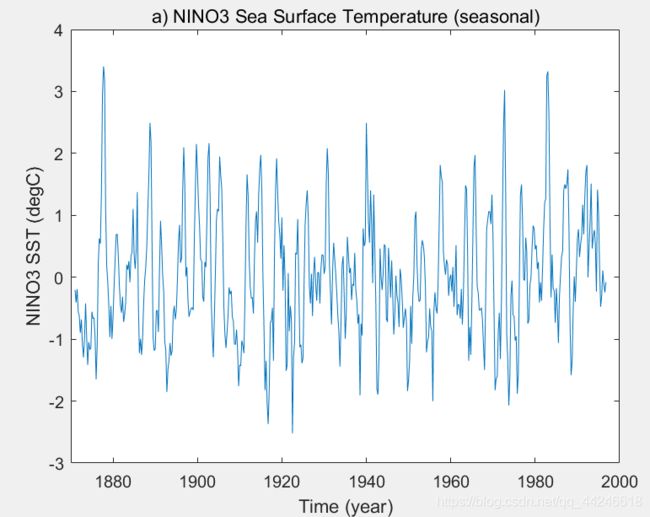
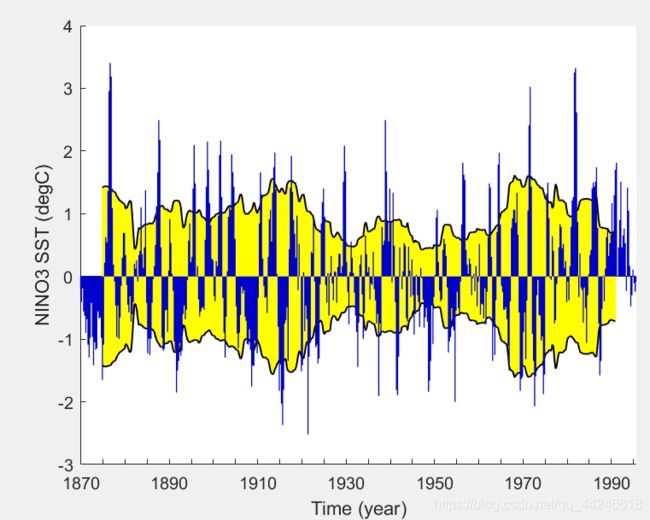
求滑动窗口为十年时的方差包络线,如下图所示:
可知,SST为非平稳时间序列

相关代码如下:

[E_SSTA , D_SSTA] = GetED( sst ,10*4 );
figure(1)
hold on
H1=bar(5*4+1:5*4+length(D_SSTA),D_SSTA);
H2=bar(5*4+1:5*4+length(D_SSTA),-D_SSTA);
set(H1,'BarWidth',1 ,'facecolor',[1  1  0]);
set(H2,'BarWidth',1 ,'facecolor',[1  1  0]);
plot(5*4+1:5*4+length(D_SSTA),D_SSTA,'k-','linewidth',1);
plot(5*4+1:5*4+length(D_SSTA),-D_SSTA,'k-','linewidth',1);
a = bar(sst,1); 
xlabel('Time (year)')
ylabel('NINO3 SST (degC)')
axis([1 length(sst) -3 4])
set(a,'BarWidth',1 ,'facecolor',[0 0 0.8]);
x = 1.5:5*4:126*4;
y = cell(1,length(x));
y(1:4:end)={'1870','1890','1910','1930','1950','1970','1990'};
set(gca, 'XTick',x,'XTickLabel',y) ;

function [ E , D ]=GetED(X,n)
% GetED函数用于获取滑动窗口为n时的均值和方差
% X为输入数据序列
% n为滑动窗口长度
N = length(X);
if N<n
    printf("错误：滑动窗口长度大于数据序列长度。")
end

E = zeros(N-n+1,1);
D = zeros(N-n+1,1);

E(1) = mean( X(1:n) );
D(1) = var( X(1:n) );
for i=1:N-n
    E( i+1) = E(i)+ (X(i+n)-X(i) )/n ;
    D(i+1) = D(i) +(E( i+1) -E(i) )/n*( (X(i+n)+X(i))*(n-1)-2*n*E(i) + 2*X(i));
end

end

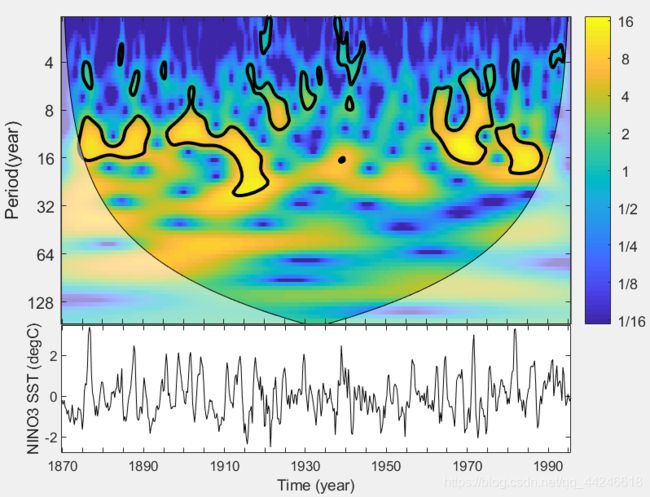
对时间序列进行连续小波变换,得到如下结果:

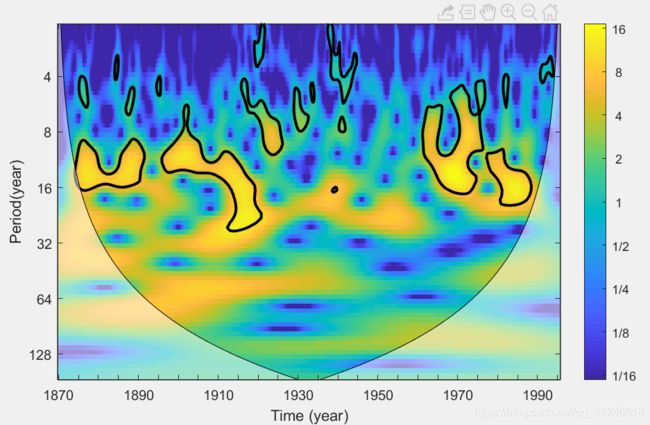
相应代码如下:(使用了工具箱)

wt(sst);
xlabel('Time (year)')
ylabel('Period(year)')
x = 1.5:5*4:126*4;
y = cell(1,length(x));
y(1:4:end)={'1870','1890','1910','1930','1950','1970','1990'};
set(gca, 'XTick',x,'XTickLabel',y) ;

相应代码如下:(同上,使用了工具箱)

figure(1)
subplot('position',[0.1 0.35 0.85 0.6])
wt(sst);
ylabel('Period(year)')
x = 1.5:5*4:126*4;
y = cell(1,length(x));
set(gca, 'XTick',x,'XTickLabel',y) ;
subplot('position',[0.1 0.1 0.745 0.25])
plot(1:length(sst),sst,'k-');
xlabel('Time (year)')
ylabel('NINO3 SST (degC)');
axis([0 length(sst) -2.8 3.5] );
x = 1.5:5*4:126*4;
y = cell(1,length(x));
y(1:4:end)={'1870','1890','1910','1930','1950','1970','1990'};
set(gca, 'XTick',x,'XTickLabel',y) ;

根据该网站相应MATLAB代码得到以下结果：