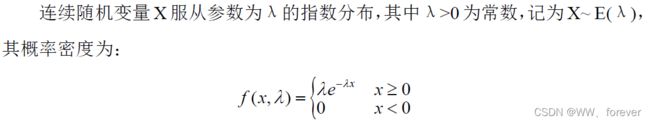MATLAB实现各种概率密度函数(概率密度/分布/逆概率分布函数)
MATLAB统计工具箱有一系列函数,函数名以pdf(probability density function) 三个字符结尾的函数用来计算常见连续分布的密度函数值或离散分布的概率函数值,函数名以cdf(cumulative density function) 三个字符结尾的函数用来计算常见分布的分布函数值,函数名以inv(inverse) 三个字符结尾的函数用来计算常见分布的逆概率密度函数。
1 常见概率分布的基本信息
MATLAB中提到的常见分布 如下表所示:
1.1 离散分布
表1 常见离散分布列表
| 名称Name | 分布 | 输入参数A | 输入参数B |
|---|---|---|---|
| bino | 二项分布(Binomial Distribution) | n 试验次数 | p 每次试验成功的概率 |
| nbin | 负二项分布(Negative binomial distribution) | ||
| geo | 几何分布(Geometric Distribution) | p 概率参数 | |
| hyge | 超几何分布(Hypergeometric Distribution) | ||
| poiss | 泊松分布(Poisson Distribution) | λ 均值 | |
| unid | 离散均匀分布(Uniform Distribution (Discrete)) | n 最大可观测值 | |
| mn | 多项分布(Multinomial distribution) |
1.2 连续分布
表2 常见连续分布列表
| 名称Name | 分布 | 输入参数A | 输入参数B | 输入参数C |
|---|---|---|---|---|
| norm | 正态分布(Normal distribution) | μ 均值 | σ 标准差 | |
| logn | 对数正态分布(Lognormal Distribution) | μ 对数值的均值 | σ 对数值的标准差 | |
| mvn | 多元正态分布 | |||
| unif | 连续均匀分布( Uniform Distribution (Continuous)) | a 下部端点(最小值) | b 上部端点(最大值) | |
| exp | 指数分布(Exponential Distribution) | μ 均值 | ||
| chi2 | 卡方均匀分布 (Chi-Square Distribution) | ν 自由度 | ||
| ncx2 | 非中心卡夫分布(Noncentral Chi-Square Distribution) | ν 自由度 | δ 非中心参数 | |
| t | t分布(Student’s t Distribution) | ν 自由度 | ||
| nct | 非中心t分布(Noncentral t Distribution) | ν 自由度 | δ 非中心参数 | |
| mvt | 多元t分布 | |||
| F | F分布(F Distribution) | ν1 分子自由度 | ν2 分母自由度 | |
| ncf | 非中心F分布(Noncentral F Distribution) | ν1 分子自由度 | ν2 分母自由度 | δ 非中心参数 |
| beta | Beta分布(Beta Distribution) | a 第一个形状参数 | b 第二个形状参数 | |
| gam | Gamma分布(Gamma Distribution) | a 形状参数 | b 尺度参数 | |
| wbl | 威布尔分布(Weibull Distribution) | a 尺度参数 | b 形状参数 | |
| rayl | 瑞利分布(Rayleigh Distribution) | b 尺度参数 | ||
| ev | 极值分布 (Extreme Value Distribution) | μ 位置参数 | σ 尺度参数 | |
| gev | 广义极值分布(Generalized Extreme Value Distribution) | k 形状参数 | σ 尺度参数 | μ 位置参数 |
| gp | 广义Pareto分布(Generalized Pareto Distribution) | k 尾部指数(形状)参数 | σ 尺度参数 | μ 阈值(位置)参数 |
在上述表中列出的常见分布名英文缩写后加上pdf,cdf,inv,就可得到计算常见分布的概率密度、分布和逆概率分布函数值的MATLAB函数。
此外,MATLAB还提供了pdf,cdf,icdf三个公共函数,如下表所列,其通过调用表1、表2重点函数来计算常见分布的概率密度、分布和逆概率分布函数值。
可参见MATLAB中文帮助中关于cdf函数的相关说明。
表3 计算概率密度、分布和逆概率分布函数值的公用函数

2 常见概率分布计算及MATLAB实现
2.1 离散分布(Discrete Distribution)
离散分布( discrete distribution):如果随机变量X的所有可能的取值是有限或者可列无穷多个,那么它分布函数的值域是离散的,对应的分布为离散分布。
常用的离散分布有二项分布、泊松分布、几何分布、负二项分布等。
2.1.1 二项分布(Binomial Distribution)
定义: 在n次独立重复的伯努利试验中,设每次试验中事件A发生的概率为p。用X表示n重伯努利试验中事件A发生的次数,则X的可能取值为0,1,…,n,且对每一个k(0≤k≤n),事件{X=k}即为“n次试验中事件A恰好发生k次”,随机变量X的离散概率分布即为二项分布(Binomial Distribution)。

PDF曲线形状: 单峰分布 随着n的增大,二项分布逐渐逼近正态分布。注意X的取值只能为整数。
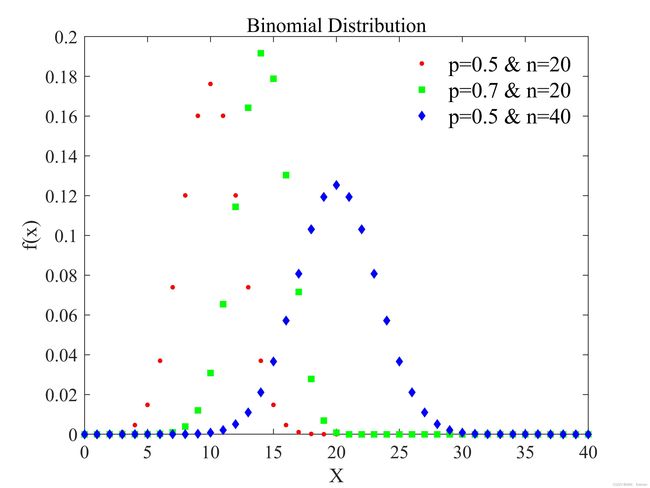
相应MTALAB实现代码:
%% 2.1.1 二项分布
% n 试验次数
% p 每次试验成功的概率
Xbino = linspace(0,40,41);
n1 = 20;
p1 = 0.5;
Pbino1 = binopdf(Xbino,n1,p1);
n2 = 20;
p2 = 0.7;
Pbino2 = binopdf(Xbino,n2,p2);
n3 = 40;
p3 = 0.5;
Pbino3 = binopdf(Xbino,n3,p3);
figure(1)
hold on;
box on;
h(1) = plot(Xbino,Pbino1,'.r','linewidth',1.5,'markersize',10);
h(2) = plot(Xbino,Pbino2,'sg','linewidth',1.5,'markersize',4,'MarkerFaceColor','g');
h(3) = plot(Xbino,Pbino3,'db','linewidth',1.5,'markersize',3,'MarkerFaceColor','b');
title("Binomial Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 ]),"p=0.5 & n=20","p=0.7 & n=20","p=0.5 & n=40",'FontSize',14);
set(hl,'Box','off','location','northeast'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.1.2 负二项分布(Negative Binomial Distribution)
负二项分布是统计学上一种离散概率分布。满足以下条件的称为负二项分布:实验包含一系列独立的实验, 每个实验都有成功、失败两种结果,成功的概率是恒定的,实验持续到r次不成功,r为正整数。
相应MTALAB实现代码:
2.1.3 几何分布(Geometric Distribution)
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
相应MTALAB实现代码:
2.1.4 超几何分布(Hypergeometric Distribution)
超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,成功抽出该指定种类的物件的次数(不放回)。称为超几何分布,是因为其形式与“超几何函数”的级数展式的系数有关。
相应MTALAB实现代码:
2.1.5 泊松分布(Poisson Distribution)
Poisson分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松(Siméon-Denis Poisson)在1838年时发表。
相应MTALAB实现代码:
2.1.6 离散均匀分布(Uniform Distribution (Discrete))
相应MTALAB实现代码:
2.1.7 多项分布(Multinomial Distribution)
相应MTALAB实现代码:
2.2 连续分布(Continuous Distribution)
连续分布(continuous distribution)连续型随机变量X的分布函数是连续的,它对应的分布为连续分布。
常用的连续分布有正态分布、均匀分布、指数分布、伽玛分布、贝塔分布等。
2.2.1 正态分布(Normal distribution)
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),最早由棣莫弗(Abraham de Moivre)在求二项分布的渐近公式中得到。C.F.高斯在研究测量误差时从另一个角度导出了它。P.S.拉普拉斯和高斯研究了它的性质。是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。其概率密度函数为正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
曲线形状: 单峰分布
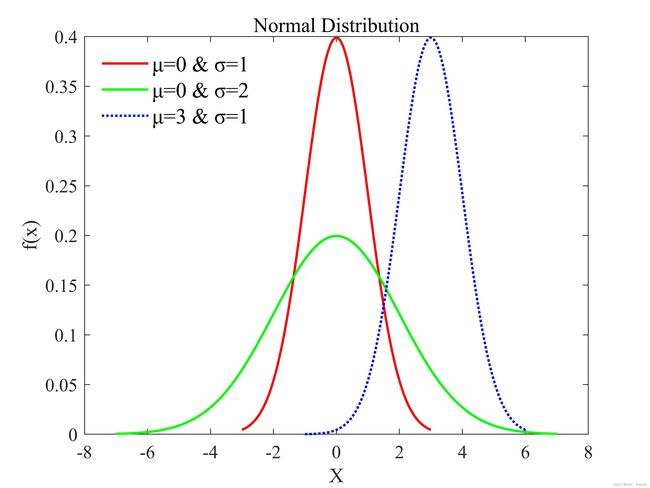
相应MTALAB实现代码:
%% 2.2.1 正态分布
% μ 均值
% σ 标准差
mu1 = 0;
sigma1 = 1;
Xnorm1 = linspace(-3,3,1000);
Ynorm1 = normpdf(Xnorm1,mu1,sigma1);
mu2 = 0;
sigma2 = 2;
Xnorm2 = linspace(-7,7,1000);
Ynorm2 = normpdf(Xnorm2,mu2,sigma2);
mu3 = 3;
sigma3 = 1;
Xnorm3 = linspace(-1,6,1000);
Ynorm3 = normpdf(Xnorm3,mu3,sigma3);
figure(221)
hold on;
box on;
h(1) = plot(Xnorm1,Ynorm1,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xnorm2,Ynorm2,'.-g','linewidth',1.5,'markersize',4,'MarkerFaceColor','g');
h(3) = plot(Xnorm3,Ynorm3,':b','linewidth',1.5,'markersize',3,'MarkerFaceColor','b');
title("Normal Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 ]),"μ=0 & σ=1","μ=0 & σ=2","μ=3 & σ=1",'FontSize',14);
set(hl,'Box','off','location','northwest'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.2.2 对数正态分布(Lognormal Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.3 多元正态分布
曲线形状:
相应MTALAB实现代码:
2.2.4 连续均匀分布( Uniform Distribution (Continuous))
曲线形状:
相应MTALAB实现代码:
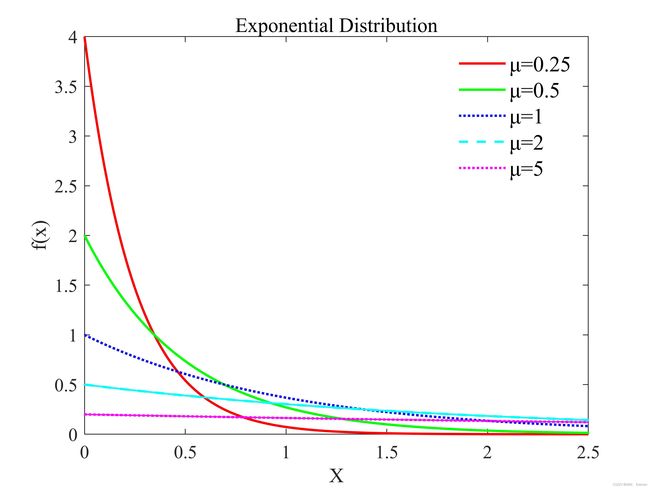
2.2.5 指数分布(Exponential Distribution)
%% 2.2.5 指数分布(Exponential Distribution)
% μ 均值
Xexp = linspace(0,2.5,500);
mu = [0.25 0.5 1 2 5];
for i=1:length(mu)
Yexp(:,i) = exppdf(Xexp, mu(i));
end
figure(225)
hold on;
box on;
h(1) = plot(Xexp,Yexp(:,1) ,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xexp,Yexp(:,2) ,'.-g','linewidth',1.5,'markersize',4);
h(3) = plot(Xexp,Yexp(:,3) ,':b','linewidth',1.5,'markersize',3);
h(4) = plot(Xexp,Yexp(:,4) ,'.--c','linewidth',1.5,'markersize',4);
h(5) = plot(Xexp,Yexp(:,5) ,':.m','linewidth',1.5,'markersize',3);
title("Exponential Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 4 5 ]),"μ=0.25","μ=0.5","μ=1","μ=2","μ=5",'FontSize',14);
set(hl,'Box','off','location','northeast'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.2.6 卡方分布(Chi-Square Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.7 非中心卡方分布(Noncentral Chi-Square Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.8 t分布(Student’s t Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.9 非中心t分布(Noncentral t Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.10 多元t分布
曲线形状:
相应MTALAB实现代码:
2.2.11 F分布(F Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.12 非中心F分布(Noncentral F Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.13 Beta分布(Beta Distribution)
曲线形状:
相应MTALAB实现代码:
2.2.14 Gamma分布(Gamma Distribution)
伽玛分布(Gamma Distribution)是统计学的一种连续概率函数,是概率统计中一种非常重要的分布。“指数分布”和“χ2分布”都是伽马分布的特例。
Gamma分布中的参数α称为形状参数(shape parameter),β称为逆尺度参数。
Gamma分布的特殊形式:
当形状参数α=1时,伽马分布就是参数为γ的指数分布,X~Exp(γ)
当α=n/2,β=1/2时,伽马分布就是自由度为n的卡方分布,X^2(n)

曲线形状:
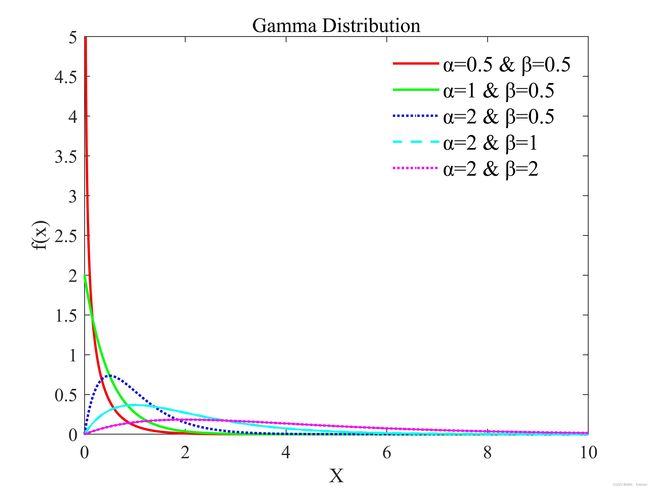
相应MTALAB实现代码:
%% 2.2.14 Gamma分布
% α 形状参数
% β 尺度参数
Xgam = linspace(0,10,1000);
alfa1 = 0.5;
beta1 = 0.5;
Ygam1 = gampdf(Xgam, alfa1 ,beta1);
alfa2 = 1;
beta2 = 0.5;
Ygam2 = gampdf(Xgam, alfa2 ,beta2);
alfa3 = 2;
beta3 = 0.5;
Ygam3 = gampdf(Xgam, alfa3 ,beta3);
alfa4 = 2;
beta4 = 1;
Ygam4 = gampdf(Xgam, alfa4 ,beta4);
alfa5 = 2;
beta5 = 2;
Ygam5 = gampdf(Xgam, alfa5 ,beta5);
figure(2214)
hold on;
box on;
h(1) = plot(Xgam,Ygam1,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xgam,Ygam2,'.-g','linewidth',1.5,'markersize',4,'MarkerFaceColor','g');
h(3) = plot(Xgam,Ygam3,':b','linewidth',1.5,'markersize',3,'MarkerFaceColor','b');
h(4) = plot(Xgam,Ygam4,'.--c','linewidth',1.5,'markersize',4,'MarkerFaceColor','g');
h(5) = plot(Xgam,Ygam5,':.m','linewidth',1.5,'markersize',3,'MarkerFaceColor','b');
title("Gamma Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 4 5 ]),"α=0.5 & β=0.5","α=1 & β=0.5","α=2 & β=0.5","α=2 & β=1","α=2 & β=2",'FontSize',14);
set(hl,'Box','off','location','northeast'); % SouthEast NorthWest
axis([0 10 0 5]);
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.2.15 威布尔分布(Weibull Distribution)
韦布尔分布,即韦伯分布(Weibull distribution),又称韦氏分布或威布尔分布,是可靠性分析和寿命检验的理论基础。

Weibull distribution与很多分布都有关系。如,当k=1,它是指数分布;k=2且时,是Rayleigh distribution(瑞利分布)。
曲线形状:

相应MTALAB实现代码:
%% 2.2.15 威布尔分布(Weibull Distribution)
% λ 尺度(比例)参数
% k 形状参数
Xwbl = linspace(0,2.5,500);
lambda = [1 1 1 1 2 2];
k = [0.5 1 1.5 5 1 5] ;
for i=1:length(lambda)
Ywbl(:,i) = wblpdf(Xwbl, lambda(i) , k(i));
end
figure(2215)
hold on;
box on;
h(1) = plot(Xwbl,Ywbl(:,1) ,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xwbl,Ywbl(:,2) ,'.-g','linewidth',1.5,'markersize',4);
h(3) = plot(Xwbl,Ywbl(:,3) ,':b','linewidth',1.5,'markersize',3);
h(4) = plot(Xwbl,Ywbl(:,4) ,'.--c','linewidth',1.5,'markersize',4);
h(5) = plot(Xwbl,Ywbl(:,5) ,':.m','linewidth',1.5,'markersize',3);
h(6) = plot(Xwbl,Ywbl(:,6) ,'-y','linewidth',1.5);
title("Weibull Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 4 5 6 ]),"λ=1 & k=0.5","λ=1 & k=1","λ=1 & k=1.5","λ=1 & k=5","λ=2 & k=1","λ=2 & k=5",'FontSize',14);
set(hl,'Box','off','location','northeast'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.2.16 瑞利分布(Rayleigh Distribution)
瑞利分布(Rayleigh Distribution):当一个随机二维向量的两个分量呈独立的、均值为0,有着相同的方差的正态分布时,这个向量的模呈瑞利分布。
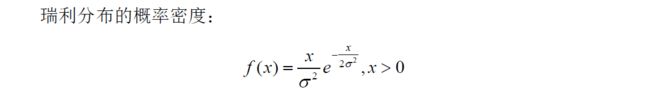
曲线形状: 单峰

相应MTALAB实现代码:
%% 2.2.16 瑞利分布(Rayleigh Distribution) rayl
% b 尺度参数
b = [0.5 1 2 3 4];
Xrayl = linspace(0,10,1000);
for i=1:length(b)
Yrayl(:,i) = raylpdf(Xrayl, b(i) );
end
figure(2216)
hold on;
box on;
h(1) = plot(Xrayl,Yrayl(:,1) ,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xrayl,Yrayl(:,2) ,'.-g','linewidth',1.5,'markersize',4);
h(3) = plot(Xrayl,Yrayl(:,3) ,':b','linewidth',1.5,'markersize',3);
h(4) = plot(Xrayl,Yrayl(:,4) ,'.--c','linewidth',1.5,'markersize',4);
h(5) = plot(Xrayl,Yrayl(:,5) ,':.m','linewidth',1.5,'markersize',3);
title("Rayleigh Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 4 5 ]),"σ=0.5","σ=1","σ=2","σ=3","σ=4",'FontSize',14);
set(hl,'Box','off','location','northeast'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.2.17 极值分布 (Extreme Value Distribution)
极值分布是指在概率论中极大值(或者极小值)的概率分布,从很多个彼此独立的值中挑出来的各个极大值应当服从的概率密度分布数f(x)。
曲线形状: 单峰
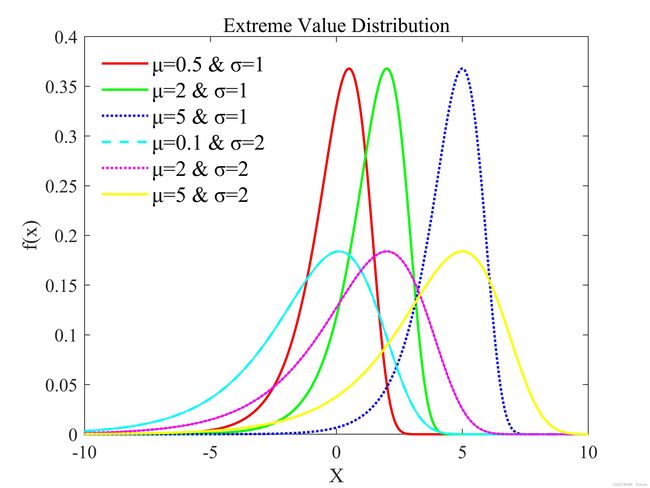
显然**μ(位置参数)**决定了曲线的极值位置,σ(尺度参数) 决定了扁平程度,类似于正态分布中方差。
相应MTALAB实现代码:
%% 2.2.17 极值分布 (Extreme Value Distribution) ev
% μ 位置参数
% σ 尺度参数
Xev = linspace(-10,10,2000);
mu = [0.5 2 5 0.1 2 5];
sigma = [1 1 1 2 2 2];
for i=1:length(mu)
Yev(:,i) = evpdf(Xev, mu(i) , sigma(i));
end
figure(2217)
hold on;
box on;
h(1) = plot(Xev,Yev(:,1) ,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xev,Yev(:,2) ,'.-g','linewidth',1.5,'markersize',4);
h(3) = plot(Xev,Yev(:,3) ,':b','linewidth',1.5,'markersize',3);
h(4) = plot(Xev,Yev(:,4) ,'.--c','linewidth',1.5,'markersize',4);
h(5) = plot(Xev,Yev(:,5) ,':.m','linewidth',1.5,'markersize',3);
h(6) = plot(Xev,Yev(:,6) ,'-y','linewidth',1.5);
title("Extreme Value Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 4 5 6 ]),"μ=0.5 & σ=1","μ=1 & σ=1","μ=5 & σ=1","μ=0.1 & σ=2","μ=2 & σ=2","μ=5 & σ=2",'FontSize',14);
set(hl,'Box','off','location','northwest'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
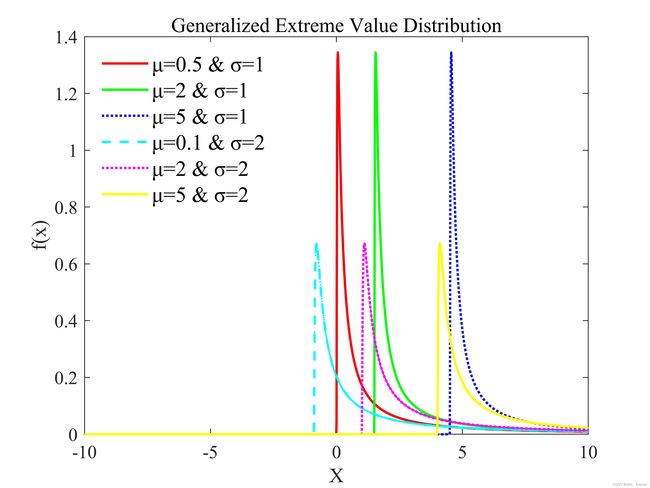
2.2.18 广义极值分布(Generalized Extreme Value Distribution)
曲线形状:
(形状参数k=0.1时)
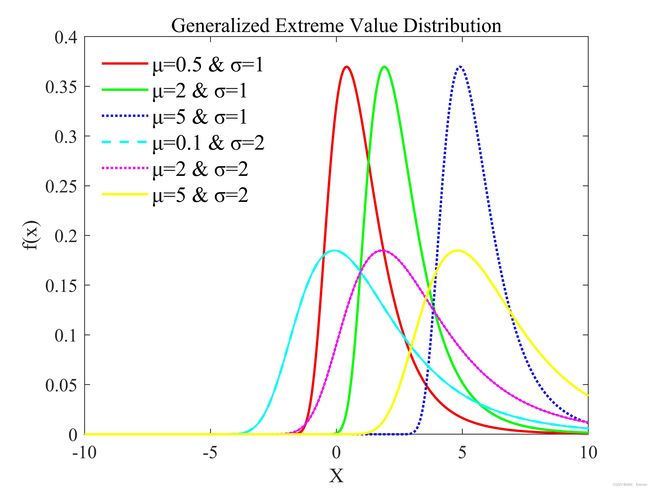
(形状参数k=1时)

(形状参数k=2时)
相应MTALAB实现代码:
%% 2.2.18 广义极值分布(Generalized Extreme Value Distribution) gev
% k 形状参数
% μ 位置参数
% σ 尺度参数
Xgev = linspace(-10,10,2000);
% k = [0.1 0.1 0.1 0.1 0.1 0.1];
% k = [1 1 1 1 1 1];
k = [2 2 2 2 2 2];
mu = [0.5 2 5 0.1 2 5];
sigma = [1 1 1 2 2 2];
for i=1:length(mu)
Ygev(:,i) = gevpdf(Xgev, k(i), sigma(i), mu(i) );
end
figure(2218)
hold on;
box on;
h(1) = plot(Xgev,Ygev(:,1) ,'-r','linewidth',1.5,'markersize',12);
h(2) = plot(Xgev,Ygev(:,2) ,'.-g','linewidth',1.5,'markersize',4);
h(3) = plot(Xgev,Ygev(:,3) ,':b','linewidth',1.5,'markersize',3);
h(4) = plot(Xgev,Ygev(:,4) ,'.--c','linewidth',1.5,'markersize',4);
h(5) = plot(Xgev,Ygev(:,5) ,':.m','linewidth',1.5,'markersize',3);
h(6) = plot(Xgev,Ygev(:,6) ,'-y','linewidth',1.5);
title("Generalized Extreme Value Distribution")
xlabel("X");
ylabel("f(x)");
hl = legend(h([1 2 3 4 5 6 ]),"μ=0.5 & σ=1","μ=2 & σ=1","μ=5 & σ=1","μ=0.1 & σ=2","μ=2 & σ=2","μ=5 & σ=2",'FontSize',14);
set(hl,'Box','off','location','northwest'); % SouthEast NorthWest
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
2.2.19 广义Pareto分布(Generalized Pareto Distribution)
曲线形状:
相应MTALAB实现代码:
3 其它概率分布计算及MATLAB实现
3.1 PⅢ分布(Pearson type Ⅲ)
PⅢ分布是我国水文统计中最常用到的水文频率曲线线型,其能较好地拟合中国大部分地区的暴雨和洪水等系列。

PⅢ分布相关参数拟合、密度函数、累计分布函数可参见另一篇文章。
参考
参考书籍: 《MATLAB统计分析与应用:40个案例分析》