数字图像处理——第八章 图像压缩

图像压缩

图像压缩所解决的问题是尽量减少表示数字图像时需要的数据量。减少数据量的基本原理是除去其中多余的数据。

1 图像压缩基础

术语“数据压缩”指减少表示给定信息的量所需的数据量。数据和信息之间必须给予明确的区分。数据是信息传递的手段，对相同数量的信息可以以不同数量的数据表示。

数据冗余是数字图像压缩的主要问题。如果n1和n2代表两个表示相同信息的数据集合中所携载的信息单元的数量，则第一个数据集合（用n1表示的集合）的相对数据冗余RD可以定义为：
这里G通常称为压缩率，定义为：

在数字图像压缩中，可以确定三种基本的数据冗余并加以利用：编码冗余、像素间冗余和心理视觉冗余。当这三种冗余中的一种或多种得到减少或者消除时，就实现了数据压缩。

1.1 编码冗余

一种解释编码冗余的方法是运用信息论的相关知识。
信息论的基本前提是信息的产生可以被模拟为一个概率过程，这个过程可以用与我们直觉相一致的方法度量。依照这个假设，发生概率为P(E)的随机事件E被认为是包含：
的信息单元。如果底数选择为2，信息单元的单位是比特。量I(E)通常被称为E的自信息。一般来讲，归因于事件E的自信息量与E的概率的关系是反向的。

如果一个信源A，可能发出的符号集{a1,a2,…,aJ}集合中的元素表示为aj，称为符号或字符。信源产生符号的时间概率是P(aj)，且有：
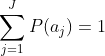信源输出的平均信息，表示为为H(z)，
这个量被称为信源的不定度或熵。它定义了观察单个信源输出得到的平均信息量。

对于图像来说，可以假设一个离散随机变量表示图像灰度级，并且每个rk出现的概率为Pr(rk)。
这里L是灰度级数，nk是第k个灰度级在图像中出现的次数，n是图像中的像素总数。如果用于表示每个rk值的比特数为l(rk)，则表达每个像素所需的平均比特数为：
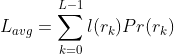就是说，将表示每个灰度级所用的比特数和灰度级出现的概率相乘，将所得乘积相加后得到不同灰度级值的平均码字长度。根据无失真编码定理，如果某种编码的平均比特数越接近熵，则编码冗余越小。

1.2 像素间冗余

像素间冗余是一种与像素间相关性有直接联系的数据冗余。

对于任何给定像素的值可以根据与这个像素相邻的像素进行适当的预测，所以由单个像素所携载的信息相对较少。单一像素对于一幅图像的多数视觉贡献是多余的，他的值可以通过以与其相邻的像素值为基础进行推测。

为了减少图像中的像素间冗余，通常用于人类观察和解释的二位像素阵列必须变换为更有效的形式。例如，相邻像素之间的差异可以用来描绘图像。这种类型变换被认为是映射。如果初试图像元素可以根据经过变换的数据集合进行重构，则称这些映射为可逆映射。

1.3 心理视觉冗余

眼睛对所有视觉信息感受的灵敏度不同。在正常的视觉处理过程中各种信息的相对重要程度不同。那些不十分重要的信息称做心理视觉冗余。这些冗余在不会削弱图像感知质量的情况下可以消除。

心理视觉冗余来自先前讨论的冗余的基本差异。与编码冗余和像素间冗余不同，心理视觉冗余是与真实的或可定量的视觉信息相联系的。因为对于正常的视觉处理过程，信息本身不是本质，所以消除心理视觉冗余是可能的。消除心理视觉冗余数据会导致一定量信息的丢失，通常是在称为“量化”的过程。使用这个过程，可以大大改善图像的表现效果。

1.4 保真度准则

评估保真度的两类准则是：（1）客观保真度准则和（2）主观保真度准则。

当信息损失的程度可以表示成初始图像或输入图像以及先被压缩而后被解压缩的输出图像的函数时，就说这个函数是基于客观保真度准则的。主观评估是通过向典型的观察者显示典型的解压缩图像并将他们的评估结果进行平均得到的。

尽管客观保真度准则提供了一种简单便捷的评估信息损失的机理，但大部分解压缩图像最终还是由人来进行观察的。所以，使用观察者的主观评估衡量图像品质通常是更为适当的。

1.5 图像压缩模型

图像压缩系统是由两个不同的功能部分组成的：一个是编码器一个是解码器。编码器执行压缩操作，解码器执行解压缩操作。

信源编码器的任务是减少或消除输入图像中的编码冗余、像素间冗余或心理视觉冗余。特定的应用和与之相连的保真度准则要求规定了在给定情况下使用的最佳编码方法。

信源解码器包含一个符号解码器和一个反向转换器。这些模块的运行次序和编码器的符号编码器和转换模块的操作次序相反。因为量化过程导致了不可逆的信息损失，反向量化器模块不包含在通常的信源解码器模型中。

2 无损压缩方法

无损压缩方法通常由两种彼此独立的操作组成：（1）为减少像素间冗余，建立一种可替代的图像表达方式（2）对这种表达方式进行编码以便消除编码冗余。

2.1 变长编码

无误差图像压缩的最简单的方法就是减少仅有的编码冗余。编码冗余通常存在于图像灰度级的自然二进制编码过程中，利用变长编码结构，可以把最短的码字赋予出现概率最大的灰度级。

变长编码必须保证能正确的解码，不能任意的按分配概率编码。

2.2 B编码

B编码中每个码字由延伸比特和信息比特组成，延伸比特的作用是实现码字分割。B编码对信源符号进行排列以便符号的概率呈单调递减的顺序，再为符号分配编码，一个延伸比特加n个信息比特。

一幅6灰度级的数字图像的直方图如下：
（1）B1编码
若一幅图像片段为0,1,3,2，则可编码为10,01,1011,0000或00,11,0001,1010。可知B1编码的平均编码长度为2.6。

2.3 霍夫曼编码

霍夫曼编码对每个信源符号生成可能的最小数量的编码符号。

霍夫曼编码的步骤：

1. 将需要考虑的符号概率进行排序
2. 将具有最低概率的符号联结为一个单一的符号，用这个符号在信源化简的下一步中替代联结之前的两个符号。
3. 重复1,2步骤直到信源只有两个符号
4. 对每个化简后的信源进行编码，从最小的信源开始，一直工作到原始的信源。

一幅6灰度级的数字图像的直方图如下：
信源化简的过程如下：
接下来对每个化简后的信源进行编码：
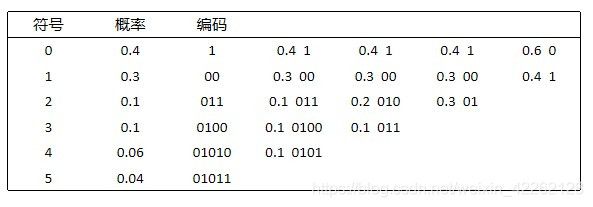最后得到的平均编码长度为2.2比特。

使用霍夫曼编码需要注意的问题：

1. 霍夫曼编码是可变长度码，因此很难随意查找或调用压缩文件中的内容，然后再译码。
2. 霍夫曼编码没有错误保护功能，如果码串中有错误，哪怕仅是1位错误都可能造成后边的译码错误，这种现象称为错误传播。

2.4 算术编码

算术编码是一种非块码，信源符号和码字之间是不存在一一对应的关系的。

算术编码是给整个信源符号序列分配一个单一的算术码字。这个码字本身定义了一个介于0到1之间的实数。因为这种技术不像霍夫曼编码方法那样要求将每个信源符号转换成整数的编码，所以这种技术达到了由无噪声编码准则所设定的界限。

算术编码用到两个基本的参数：符号概率和它的编码间隔。信源符号的概率决定了压缩编码的效率，也决定了编码过程中信源符号的间隔，而这些间隔包含在0到1之间。编码过程中间隔决定了符号压缩后的输出。

算术编码器的编码过程可用下面的例子加以解释：
假设信源可能发出的符号为{A,B,C,D}，这些符号的概率为{0.1,0.4,0.2,0.3}，求符号序列“C,A,D,A,C”的算术编码。
在编码处理的开始，消息占据整个半开区间[0,1)。编码序列中第一个符号C，编码间隔被限制在[0.5,0.7）间，区间[0.5,0.7）被扩展到图形的全高度，并在区间[0.5,0.7）中根据信源符号出现的概率进行细分，而后接着处理下一个消息符号。用这种方式，符号A将子区间变窄为[0.5,0.52)，符号D又将子区间变窄为[0.514,0.52)。最后子区间变窄为[0.5143,0.51442),在这个区间中的任何数字都可以被用来表示这个消息。

在算数编码中需要注意的几个问题：

1. 需要有一定的方法指示解码器停止解码。例如增加一个消息结束指示符。
2. 由于计算机的精度不可能是无限长，溢出是一个要考虑的问题。算术编码的实际实现中通过引入尺度策略和舍入策略解决这个问题。
3. 在计算机中算术编码的结果最终使用二进制数来表示的，故算术编码也是一种对错误很敏感的编码方法，如果有以为发生错误就会导致整个消息译错。

2.5 词典编码（LZW编码）

词典编码不需要了解有关编码符号的出现的概率。词典编码的根据是数据本身包含有重复代码这个特性。

词典编码大致分为两类：
第一类词典编码的想法是企图查找正在压缩的字符序列是否在以前输入的数据中出现过，然后用已经出现的字符串代替重读的部分，他的输出仅仅是指早期出现过的字符串的“指针”。这一类词典编码所指的“词典”是指用以前处理过的数据来表示编码过程中遇到的重复部分。
第二类词典压缩算法的思想是企图从输入的数据中创建一个“短语词典”，它可以是任意信源符号的组合。编码数据过程中当遇到已经在词典中出现的“短语”时，编码器就输出这个词典中的短语的索引号。

LZW编码是一种处理图像像素间冗余的无误差压缩技术，属于第二类的词典编码，对信源符号的可变长度序列分配固定长度码字，且不需要了解有关被编码符号的出现的概率。

LZW编码算法开始时要建立初始词典，此时词典中的项仅为信源可能发出的各种单个字符。其后令当前前缀P为空，当前字符C=字符流中的下一个字符，判断当前前缀加当前字符形成的缀符串P+C是否在词典中，最后判断字符流中是否还有字符要编码。

2.6 位平面编码

单独处理图像的位平面也是一种能有效的减少像素间冗余的技术。

它是以将一幅多级图像分解为一系列二值图像并通过几种熟知的二值图像压缩方法对每幅二值图像进行压缩的原理为基础的。

一幅m比特的灰度图像具有的灰度级可以用以2为底的多项式进行表示，基于这种性质，将这类图像分解为一个二值图像集的一种简单方法就是，将多项式的m个系数分离到m个1比特的位平面中。零级位平面是通过收集每个像素的a0位生成的，而第m-1级位平面包含am-1比特或系数。

这种方法固有的缺点是图像在灰度级上稍有变化就会对位平面的复杂性产生显著的影响。例如如果一个亮度为127的像素与一个亮度为128的像素相邻，每个位平面将包含一个对应0到1的转换。

3 有损压缩方法

有损压缩是以在图像结构的准确度上做出让步而换区压缩能力增加的概念为基础的。如果产生失真是可以容忍的，则压缩能力上的增加就是有效的。

3.1 有损预测编码

有损预测编码中增加一个数字量化器，这个量化器将预测误差映射成有限范围内的输出，表示为en，这个输出确定了与有损预测编码想联系的压缩和失真的量。

3.2 变换编码

在变换编码中，一种可逆线性变换（如傅里叶变换）用于将图像映射到变换系数集，然后这些系数被量化和编码。对大多数自然图像，大量系数的量级很小，可以进行不是很精确的量化（或完全丢失），几乎不会产生多少图像失真。

在变换编码系统中，解码器的执行步骤（除了量化函数以外）与编码器相反。编码器执行四种相对简单的操作：子图分解、变换、量化和编码。一幅NN大小的输入图像首先被分解为nn的子图像，这些子图像进而被变换生成(N/n)^2个子图像变换阵列。变换处理的目的是将每幅子图像中的像素进行相关分解，或用最少了的变换系数包含尽可能多的信息。在量化阶段有选择地消除或更粗略的量化带有最少信息的系数。这些系数对重构子图像质量的影响很小。在给定的应用中选择特定的变换取决于可容忍的重构误差的大小和可用的计算资源。在变换系数的量化过程中实现了压缩。

4 JPEG压缩

压缩步骤如下：

1. 图像首先被细分为8*8的像素块，这些像素块进行从左到右从上到下的处理。
2. 对块中的每个像素减去2^(n-1)，对于256灰度级的图像即减去128.
3. 计算块的二维离散余弦变换。
4. 量化，对变换系数进行均匀量化。
5. 使用z形编排，形成一个量化系数的一维序列。
6. 非零的AC系数是使用规定了系数值和处在前面位置的零的个数的一种变长编码进行编码的。DC系数相对于前面子图像的DC系数进行不同的编码。

下面介绍两个M文件：

%im2jpeg源程序
function y=im2jpeg(x,quality)
%im2jpeg使用jpeg解压近似值压缩图像
%y=im2jpeg(x,quality)在8*8块DCT转换、系数量化和霍夫曼符号编码下寓所图像x
%输入quality决定的是已给丢失和压缩的信息数量。
%y是编码结构域：

%Y.size              x的类型
%Y.numblock    8*8编码块的数量
%Y.quality         质量因素(百分比)
%Y.huffman      由mat2huff返回霍曼夫编码结构

%也看jpeg2im

error(nargchk(1,2,nargin));%检查输入参数
if ndims(x)~=2 | ~isreal(x) | ~isnumeric(x) | ~isa(x,'uint8') 
    error('The input must be a UINT8 image.');
end
if nargin<2
    quality=1;%设置默认值
end

m=[16 11 10 16 24 40 51 61%jpeg标准化数组和重排列的zig-zag模型
    12 12 14 19 26 58 60 55
    14 13 16 24 40 57 69 56
    14 17 22 29 51 87 80 62
    18 22 37 56 68 109 103 77
    24 35 55 64 81 104 113 92
    49 64 78 87 103 121 120 101
    72 64 78 87 103 121 120 101
    72 92 95 98 112 100 103 99]*quality;

order=[1 9 2 3 10 17 25 18 11 4 5 12 19 26 33 ...
    41 34 27 20 13 6 7 14 21 28 35 42 49 57 50 ...
    43 36 29 22 15 8 16 23 30 37 44 51 58 59 52 ...
    62 63 56 64];

[xm,xn]=size(x);%得到输出大小
x=double(x)-128;%水平平移输入
t=dctmtx(8);%计算8*8DCT矩阵

%计算8*8块DCT和量化系数
y=blkproc(x,[8 8],'P1*x*P2',t,t');
y=blkproc(y,[8 8],'round(x./P1)',m);

y=im2col(y,[8 8],'distinct');%打破8*8块进入列
xb=size(y,2);%得到块数
y=y(order,:);%重排列列元素

eob=max(x(:))+1;%创造最后的块符号
r=zeros(numel(y)+size(y,2),1);
count=0;
for j=1:xb%每次处理1个块(列)
    i=max(find(y(:,j)));%找到最后一个非零元素
    if isempty(i)%没有非零块元素
        i=0;
    end
    p=count+1;
    q=p+i;
    r(p:q)=[y(1:i,j);eob];%截断结尾为0，加eob到输出变量
    count=count+i+1;
end
r((count+1):end)=[];%删除未使用过的r的部分

y.size=uint16([xm xn]);
y.numblocks=uint16(xb);
y.quality=uint16(quality*100);
y.huffman=mat2huff(r);

function x = jpeg2im(y) 
%IM2JPEG Compresses an image using a JPEG approximation.
%   Y = IM2JPEG(X, QUALITY) compresses image X based on 8 x 8 DCT
%   transforms, coefficient quantization, and Huffman symbol
%   coding. Input QUALITY determines the amount of information that
%   is lost and compression achieved.  Y is an encoding structure
%   containing fields: 
%
%      Y.size      Size of X
%      Y.numblocks Number of 8-by-8 encoded blocks
%      Y.quality   Quality factor (as percent)
%      Y.huffman   Huffman encoding structure, as returned by
%                  MAT2HUFF
%
%   See also JPEG2IM.
 
%   Copyright 2002-2006 R. C. Gonzalez, R. E. Woods, & S. L. Eddins
%   Digital Image Processing Using MATLAB, Prentice-Hall, 2004
%   $Revision: 1.5 $  $Date: 2006/07/15 20:44:34 $
%
%   Revised: 3/20/06 by R.Woods to correct an 'eob' coding problem, to
%   check the 'quality' input for <= 0, and to fix a warning when
%   struct y is created.
 
error(nargchk(1, 1, nargin));             % Check input arguments
 
 
m = [16 11  10  16  24  40  51  61        % JPEG normalizing array
     12  12  14  19  26  58  60  55       % and zig-zag redordering
     14  13  16  24  40  57  69  56       % pattern.
     14  17  22  29  51  87  80  62
     18  22  37  56  68  109 103 77
     24  35  55  64  81  104 113 92
     49  64  78  87  103 121 120 101
     72  92  95  98  112 100 103 99];
 
order = [1 9  2  3  10 17 25 18 11 4  5  12 19 26 33  ...
        41 34 27 20 13 6  7  14 21 28 35 42 49 57 50  ...
        43 36 29 22 15 8  16 23 30 37 44 51 58 59 52  ...
        45 38 31 24 32 39 46 53 60 61 54 47 40 48 55  ...
        62 63 56 64];
 
rev=order;
for k=1:length(order)
    rev(k)=find(order==k);
end
m=double(y.quality)/100*m;
xb=double(y.numblocks);
sz=double(y.size);
xn=sz(2);
xm=sz(1);
x=huff2mat(y.huffman);
eob = max(x(:));               % Create end-of-block symbol
 
z = zeros(64,xb) ;k=1;
 
for j = 1:xb                       % Process 1 block (col) at a time
 for i=1:64
     if x(k)==eob
         k=k+1;
     end
 end
end
z=z(rev,:);
x=col2im(z,[8 8],[xm xn],'distinct');
x=blkproc(x,[8 8],'x.*P1',m);
t=dctmtx(8);
x=dlkproc(x,[8 8],'P1* x *P2',t',t);
x=x+double(2^(y.bits-1));
if y.bits<=8
    x=uint8(x);
else
    x=uint16(x);
end

在第一个M文件中，函数im2jpeg处理输入图像x的不同8*8块。两个简化函数blkproc和im2col用于简化计算，其中blkproc自动完成块中各图像的整个处理，im2col通常用于重排输入，以便操作可用一种简单且更为有效的方式来编码。

相似的块处理和基于矩阵的变换被用来对一幅im2jpeg压缩过的图像解压缩。函数jpeg2im执行需要的反操作序列。

图1 JPEG压缩

如图1显示了两张对单色图像进行JPEG压缩的近似结果，1-1和1-2可以看出一些轻微干扰，而放大后可以看到1-3和1-1没有发生太大变化，而1-4和1-2相比则相差更大，所以通过放大部分可以更好地评估重建图像间的细微差别。

总结

图像作为信息的重要表现形式，其大数据量不仅超出了计算机的存储和处理能力，更是当前通信信道的传输速率所不及，为了存储就必须进行压缩。

一般原始图像中存在很大的冗余度，数据冗余就是代表无用信息或重复表示了其他数据已经表示过得信息的数据，分为编码冗余、像素间冗余和视觉心理冗余。

图像压缩编码分类如下：

图2 图像压缩编码分类

在无损压缩编码中：词典编码的基本思想是去除像素间冗余，一边进行编码输出，同时生成字典，如果发现已经在字典中出现的连续符号，就用字典的条目来表示；霍夫曼编码是对于大概率的信息符号编以短字长的码，对于小概率的新媳妇号编以长字长的码，，是无失真编码中效率比较高的一种编码方法，但其缺点在于信源缩减过程复杂，运算量大；相比于算术编码，和霍夫曼编码类似，都属于变长编码，但算术编码可以分配带有小数比特的数目信符，其更接近于最优熵编码，压缩性能优于霍夫曼编码。

在有损压缩编码中，有损预测编码把每一个像素灰度值用先前扫描过得像素灰度值去减，求出他们的差值再被量化和编码传送，接收端再将此差值与预测值相加重建原始图像像素的信号。由于量化和传送仅是误差信号，根据一般扫描图像信号在空间及时间邻域内各像素的相关性，预测误差分布更集中，即熵值比原来图像小得以实现压缩；变换编码则是把图像从空间域转换为能量比较集中的变换域系数，然后对变换系数进行编码，从而达到缩减比特率的效果。