傅里叶级数与傅里叶变换_Part0_欧拉公式证明+三角函数和差公式证明
傅里叶级数与傅里叶变换_Part0_欧拉公式证明+三角函数和差公式证明
1、欧拉公式证明
欧拉公式: e i θ = cos θ + i sin θ {e^{i\theta }} = \cos \theta + i\sin \theta eiθ=cosθ+isinθ , 其中, i = − 1 i = \sqrt { - 1} i=−1
欧拉公式在控制理论和动态系统分析当中,起到了非常重要的作用。
下面用一种简单的方式证明一下欧拉公式。
证明:
设函数: f ( θ ) = e i θ cos θ + i sin θ f\left( \theta \right) = \frac{{{e^{i\theta }}}}{{\cos \theta + i\sin \theta }} f(θ)=cosθ+isinθeiθ
对 f ( θ ) f\left( \theta \right) f(θ)求导,复合函数求导: ( u v ) ′ = u ′ v − u v ′ v 2 {\left( {\frac{u}{v}} \right)^\prime } = \frac{{u'v - uv'}}{{{v^2}}} (vu)′=v2u′v−uv′
得
f ′ ( θ ) = i e i θ ( cos θ + i sin θ ) − e i θ ( − sin θ + i cos θ ) ( cos θ + i sin θ ) 2 = i e i θ cos θ − e i θ sin θ + e i θ sin θ − e i θ i cos θ ( cos θ + i sin θ ) 2 = 0 \begin{aligned} f'\left( \theta \right) &= \frac{{i{e^{i\theta }}\left( {\cos \theta + i\sin \theta } \right) - {e^{i\theta }}\left( { - \sin \theta + i\cos \theta } \right)}}{{{{\left( {\cos \theta + i\sin \theta } \right)}^2}}} \\ &= \frac{{i{e^{i\theta }}\cos \theta - {e^{i\theta }}\sin \theta + {e^{i\theta }}\sin \theta - {e^{i\theta }}i\cos \theta }}{{{{\left( {\cos \theta + i\sin \theta } \right)}^2}}}\\ & = 0 \end{aligned} f′(θ)=(cosθ+isinθ)2ieiθ(cosθ+isinθ)−eiθ(−sinθ+icosθ)=(cosθ+isinθ)2ieiθcosθ−eiθsinθ+eiθsinθ−eiθicosθ=0
f ′ ( θ ) = 0 ⇒ f ( θ ) f'\left( \theta \right) = 0 \Rightarrow f\left( \theta \right) f′(θ)=0⇒f(θ)是常数。
∴ f ( θ ) = f ( 0 ) = e i 0 cos 0 + i sin 0 = 1 1 + 0 = 1 f\left( \theta \right) = f\left( 0 \right) = \frac{{{e^{i0}}}}{{\cos 0 + i\sin 0}} = \frac{1}{{1 + 0}} = 1 f(θ)=f(0)=cos0+isin0ei0=1+01=1
e i θ cos θ + i sin θ = 1 ⇒ e i θ = cos θ + i sin θ \frac{{{e^{i\theta }}}}{{\cos \theta + i\sin \theta }} = 1 \Rightarrow {e^{i\theta }} = \cos \theta + i\sin \theta cosθ+isinθeiθ=1⇒eiθ=cosθ+isinθ
证明完毕!
2、用欧拉公式证明三角函数的和差公式
sin ( α + β ) = sin ( α ) cos ( β ) + cos ( α ) sin ( β ) ( 1 ) sin ( α − β ) = sin ( α ) cos ( β ) − cos ( α ) sin ( β ) ( 2 ) cos ( α + β ) = cos ( α ) cos ( β ) − sin ( α ) sin ( β ) ( 3 ) cos ( α − β ) = cos ( α ) cos ( β ) + sin ( α ) sin ( β ) ( 4 ) \begin{array}{l} \sin \left( {\alpha + \beta } \right) = \sin \left( \alpha \right)\cos \left( \beta \right) + \cos \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 1 \right)\\ \sin \left( {\alpha - \beta } \right) = \sin \left( \alpha \right)\cos \left( \beta \right) - \cos \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 2 \right)\\ \cos \left( {\alpha + \beta } \right) = \cos \left( \alpha \right)\cos \left( \beta \right) - \sin \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 3 \right)\\ \cos \left( {\alpha - \beta } \right) = \cos \left( \alpha \right)\cos \left( \beta \right) + \sin \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 4 \right) \end{array} sin(α+β)=sin(α)cos(β)+cos(α)sin(β)(1)sin(α−β)=sin(α)cos(β)−cos(α)sin(β)(2)cos(α+β)=cos(α)cos(β)−sin(α)sin(β)(3)cos(α−β)=cos(α)cos(β)+sin(α)sin(β)(4)
根据欧拉公式 e i θ = cos θ + i sin θ {e^{i\theta }} = \cos \theta + i\sin \theta eiθ=cosθ+isinθ
e i ( α + β ) = cos ( α + β ) + i sin ( α + β ) e i α = cos α + i sin α e i β = cos β + i sin β e i ( α + β ) = e i α ⋅ e i β = ( cos α + i sin α ) ( cos β + i sin β ) = cos α cos β + cos α sin β i + sin α cos β i − sin α sin β = ( cos α cos β − sin α sin β ) + i ( cos α sin β + sin α cos β ) = cos ( α + β ) + i sin ( α + β ) \begin{aligned} {e^{i\left( {\alpha + \beta } \right)}} &= \cos \left( {\alpha + \beta } \right) + i\sin \left( {\alpha + \beta } \right)\\ {e^{i\alpha }} &= \cos \alpha + i\sin \alpha \\ {e^{i\beta }} &= \cos \beta + i\sin \beta \\ {e^{i\left( {\alpha + \beta } \right)}} &= {e^{i\alpha }} \cdot {e^{i\beta }} = \left( {\cos \alpha + i\sin \alpha } \right)\left( {\cos \beta + i\sin \beta } \right)\\ &= \cos \alpha \cos \beta + \cos \alpha \sin \beta i + \sin \alpha \cos \beta i - \sin \alpha \sin \beta \\ &= \left( {\cos \alpha \cos \beta - \sin \alpha \sin \beta } \right) + i\left( {\cos \alpha \sin \beta + \sin \alpha \cos \beta } \right)\\ &= \cos \left( {\alpha + \beta } \right) + i\sin \left( {\alpha + \beta } \right) \end{aligned} ei(α+β)eiαeiβei(α+β)=cos(α+β)+isin(α+β)=cosα+isinα=cosβ+isinβ=eiα⋅eiβ=(cosα+isinα)(cosβ+isinβ)=cosαcosβ+cosαsinβi+sinαcosβi−sinαsinβ=(cosαcosβ−sinαsinβ)+i(cosαsinβ+sinαcosβ)=cos(α+β)+isin(α+β)
两个复数相等的充要条件是它们的实部和虚部分别相等,因此
cos ( α + β ) = cos α cos β − sin α sin β sin ( α + β ) = cos α sin β + sin α cos β \begin{array}{l} \cos \left( {\alpha + \beta } \right) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \\ \sin \left( {\alpha + \beta } \right) = \cos \alpha \sin \beta + \sin \alpha \cos \beta \end{array} cos(α+β)=cosαcosβ−sinαsinβsin(α+β)=cosαsinβ+sinαcosβ
(3) 式 和(1)式证毕。
利用上述证明过程,如法炮制
e i ( α − β ) = cos ( α − β ) + i sin ( α − β ) e i α = cos α + i sin α e i β = cos β + i sin β \begin{aligned} {e^{i\left( {\alpha - \beta } \right)}} &= \cos \left( {\alpha - \beta } \right) + i\sin \left( {\alpha - \beta } \right)\\ {e^{i\alpha }} &= \cos \alpha + i\sin \alpha \\ {e^{i\beta }} &= \cos \beta + i\sin \beta \end{aligned} ei(α−β)eiαeiβ=cos(α−β)+isin(α−β)=cosα+isinα=cosβ+isinβ
e i ( α − β ) = e i α ⋅ e i ( − β ) = ( cos α + i sin α ) [ cos ( − β ) + i sin ( − β ) ] = cos α cos ( − β ) + cos α sin ( − β ) i + sin α cos ( − β ) i − sin α sin ( − β ) \begin{aligned} {e^{i\left( {\alpha - \beta } \right)}} &= {e^{i\alpha }} \cdot {e^{i\left( { - \beta } \right)}} = \left( {\cos \alpha + i\sin \alpha } \right)\left[ {\cos \left( { - \beta } \right) + i\sin \left( { - \beta } \right)} \right]\\ &= \cos \alpha \cos \left( { - \beta } \right) + \cos \alpha \sin \left( { - \beta } \right)i \\&+ \sin \alpha \cos \left( { - \beta } \right)i - \sin \alpha \sin \left( { - \beta } \right) \end{aligned} ei(α−β)=eiα⋅ei(−β)=(cosα+isinα)[cos(−β)+isin(−β)]=cosαcos(−β)+cosαsin(−β)i+sinαcos(−β)i−sinαsin(−β)
因为 cos ( x ) \cos \left( x \right) cos(x)是偶函数 , cos ( − β ) = cos ( β ) \cos \left( { - \beta } \right) = \cos \left( \beta \right) cos(−β)=cos(β)。 sin ( x ) \sin \left( x \right) sin(x)是奇函数, sin ( − β ) = − sin ( β ) \sin \left( { - \beta } \right) = - \sin \left( \beta \right) sin(−β)=−sin(β)。所以
e i ( α − β ) = cos α cos β − cos α sin β i + sin α cos β i + sin α sin β = ( cos α cos β + sin α sin β ) + i ( sin α cos β − cos α sin β ) = cos ( α − β ) + i sin ( α − β ) \begin{aligned} {e^{i\left( {\alpha - \beta } \right)}} &= \cos \alpha \cos \beta - \cos \alpha \sin \beta i + \sin \alpha \cos \beta i + \sin \alpha \sin \beta \\ &= \left( {\cos \alpha \cos \beta + \sin \alpha \sin \beta } \right) + i\left( {\sin \alpha \cos \beta - \cos \alpha \sin \beta } \right)\\ &= \cos \left( {\alpha - \beta } \right) + i\sin \left( {\alpha - \beta } \right) \end{aligned} ei(α−β)=cosαcosβ−cosαsinβi+sinαcosβi+sinαsinβ=(cosαcosβ+sinαsinβ)+i(sinαcosβ−cosαsinβ)=cos(α−β)+isin(α−β)
因此可得
cos ( α − β ) = cos α cos β + sin α sin β sin ( α − β ) = sin α cos β − cos α sin β \begin{array}{l} \cos \left( {\alpha - \beta } \right) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \\ \sin \left( {\alpha - \beta } \right) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \end{array} cos(α−β)=cosαcosβ+sinαsinβsin(α−β)=sinαcosβ−cosαsinβ
(4) 式 和(2)式证毕。
3、总结和扩展
三角函数的和差公式如下
sin ( α + β ) = sin ( α ) cos ( β ) + cos ( α ) sin ( β ) ( 1 ) sin ( α − β ) = sin ( α ) cos ( β ) − cos ( α ) sin ( β ) ( 2 ) cos ( α + β ) = cos ( α ) cos ( β ) − sin ( α ) sin ( β ) ( 3 ) cos ( α − β ) = cos ( α ) cos ( β ) + sin ( α ) sin ( β ) ( 4 ) \begin{array}{l} \sin \left( {\alpha + \beta } \right) = \sin \left( \alpha \right)\cos \left( \beta \right) + \cos \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 1 \right)\\ \sin \left( {\alpha - \beta } \right) = \sin \left( \alpha \right)\cos \left( \beta \right) - \cos \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 2 \right)\\ \cos \left( {\alpha + \beta } \right) = \cos \left( \alpha \right)\cos \left( \beta \right) - \sin \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 3 \right)\\ \cos \left( {\alpha - \beta } \right) = \cos \left( \alpha \right)\cos \left( \beta \right) + \sin \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 4 \right) \end{array} sin(α+β)=sin(α)cos(β)+cos(α)sin(β)(1)sin(α−β)=sin(α)cos(β)−cos(α)sin(β)(2)cos(α+β)=cos(α)cos(β)−sin(α)sin(β)(3)cos(α−β)=cos(α)cos(β)+sin(α)sin(β)(4)
根据三角函数的和差公式,我们推导出积化和差的公式
(1)+(2)可得 sin ( α + β ) + sin ( α − β ) = 2 sin ( α ) cos ( β ) ⇒ sin ( α ) cos ( β ) = 1 2 [ sin ( α + β ) + sin ( α − β ) ] \sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right) = 2\sin \left( \alpha \right)\cos \left( \beta \right) \Rightarrow \sin \left( \alpha \right)\cos \left( \beta \right) = \frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) + \sin \left( {\alpha - \beta } \right)} \right] sin(α+β)+sin(α−β)=2sin(α)cos(β)⇒sin(α)cos(β)=21[sin(α+β)+sin(α−β)]
(1)-(2)可得 sin ( α + β ) − sin ( α − β ) = 2 cos ( α ) sin ( β ) ⇒ cos ( α ) sin ( β ) = 1 2 [ sin ( α + β ) − sin ( α − β ) ] \sin \left( {\alpha + \beta } \right) - \sin \left( {\alpha - \beta } \right) = 2\cos \left( \alpha \right)\sin \left( \beta \right) \Rightarrow \cos \left( \alpha \right)\sin \left( \beta \right) = \frac{1}{2}\left[ {\sin \left( {\alpha + \beta } \right) - \sin \left( {\alpha - \beta } \right)} \right] sin(α+β)−sin(α−β)=2cos(α)sin(β)⇒cos(α)sin(β)=21[sin(α+β)−sin(α−β)]
(3)+(4)可得 cos ( α + β ) + cos ( α − β ) = 2 cos ( α ) cos ( β ) ⇒ cos ( α ) cos ( β ) = 1 2 [ cos ( α + β ) + cos ( α − β ) ] \cos \left( {\alpha + \beta } \right) + \cos \left( {\alpha - \beta } \right) = 2\cos \left( \alpha \right)\cos \left( \beta \right) \Rightarrow \cos \left( \alpha \right)\cos \left( \beta \right) = \frac{1}{2}\left[ {\cos \left( {\alpha + \beta } \right) + \cos \left( {\alpha - \beta } \right)} \right] cos(α+β)+cos(α−β)=2cos(α)cos(β)⇒cos(α)cos(β)=21[cos(α+β)+cos(α−β)]
(4)- (3)可得 cos ( α − β ) − cos ( α + β ) = 2 sin ( α ) sin ( β ) ⇒ sin ( α ) sin ( β ) = 1 2 [ cos ( α − β ) − cos ( α + β ) ] \cos \left( {\alpha - \beta } \right) - \cos \left( {\alpha + \beta } \right) = 2\sin \left( \alpha \right)\sin \left( \beta \right) \Rightarrow \sin \left( \alpha \right)\sin \left( \beta \right) = \frac{1}{2}\left[ {\cos \left( {\alpha - \beta } \right) - \cos \left( {\alpha + \beta } \right)} \right] cos(α−β)−cos(α+β)=2sin(α)sin(β)⇒sin(α)sin(β)=21[cos(α−β)−cos(α+β)]
同理:积化和差公式能够反向推导和差公式,下面就不赘述了
4、附一个不完全证明
下面给出一种仅适用于 α < 9 0 o \alpha < {90^o} α<90o, β < 9 0 o \beta < {90^o} β<90o, α + β < 9 0 o \alpha + \beta < {90^o} α+β<90o 的几何证明方法。 这东西很妙。
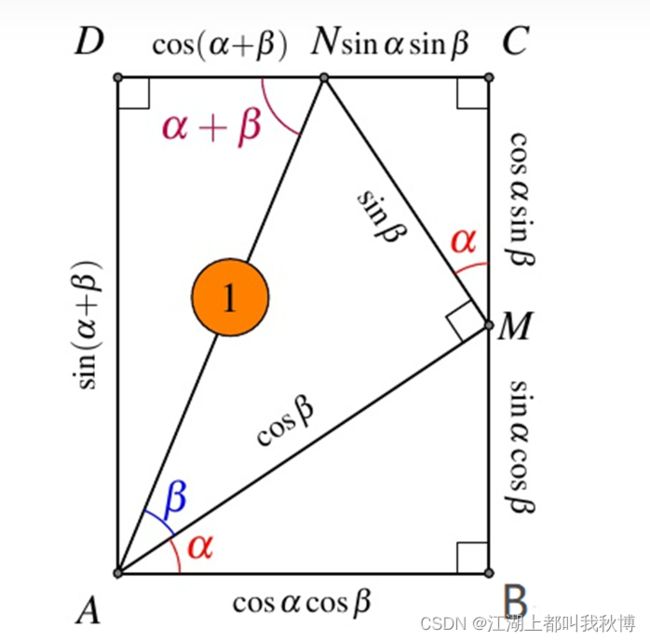
根据矩形的对边长度相等,就能得到
{ sin ( α + β ) = sin ( α ) cos ( β ) + cos ( α ) sin ( β ) ( 1 ) { cos ( α ) cos ( β ) = cos ( α + β ) + sin ( α ) sin ( β ) ⇒ cos ( α + β ) = cos ( α ) cos ( β ) − sin ( α ) sin ( β ) ( 3 ) \begin{array}{l} \left\{ {\sin \left( {\alpha + \beta } \right) = \sin \left( \alpha \right)\cos \left( \beta \right) + \cos \left( \alpha \right)\sin \left( \beta \right)} \right.{\rm{ }}\left( 1 \right)\\ \left\{ \begin{array}{l} \cos \left( \alpha \right)\cos \left( \beta \right) = \cos \left( {\alpha + \beta } \right) + \sin \left( \alpha \right)\sin \left( \beta \right)\\ \Rightarrow \cos \left( {\alpha + \beta } \right) = \cos \left( \alpha \right)\cos \left( \beta \right) - \sin \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 3 \right) \end{array} \right. \end{array} {sin(α+β)=sin(α)cos(β)+cos(α)sin(β)(1){cos(α)cos(β)=cos(α+β)+sin(α)sin(β)⇒cos(α+β)=cos(α)cos(β)−sin(α)sin(β)(3)
根据函数的奇偶性质,可以推出另外两个差公式
sin [ α + ( − β ) ] = sin ( α ) cos ( − β ) + cos ( α ) sin ( − β ) \sin \left[ {\alpha + \left( { - \beta } \right)} \right] = \sin \left( \alpha \right)\cos \left( { - \beta } \right) + \cos \left( \alpha \right)\sin \left( { - \beta } \right) sin[α+(−β)]=sin(α)cos(−β)+cos(α)sin(−β)
因为 cos ( x ) \cos \left( x \right) cos(x)是偶函数 , cos ( − β ) = cos ( β ) \cos \left( { - \beta } \right) = \cos \left( \beta \right) cos(−β)=cos(β)。 sin ( x ) \sin \left( x \right) sin(x)是奇函数, sin ( − β ) = − sin ( β ) \sin \left( { - \beta } \right) = - \sin \left( \beta \right) sin(−β)=−sin(β)。所以
sin ( α − β ) = sin ( α ) cos ( β ) − cos ( α ) sin ( β ) ( 2 ) \sin \left( {\alpha - \beta } \right) = \sin \left( \alpha \right)\cos \left( \beta \right) - \cos \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 2 \right) sin(α−β)=sin(α)cos(β)−cos(α)sin(β)(2)
同理 cos ( α − β ) = cos ( α ) cos ( β ) + sin ( α ) sin ( β ) ( 4 ) \cos \left( {\alpha - \beta } \right) = \cos \left( \alpha \right)\cos \left( \beta \right) + \sin \left( \alpha \right)\sin \left( \beta \right){\rm{ }}\left( 4 \right) cos(α−β)=cos(α)cos(β)+sin(α)sin(β)(4)
系列学习链接:欢迎大家点赞、收藏、留言讨论。
傅里叶级数与傅里叶变换_Part0_欧拉公式证明+三角函数和差公式证明
傅里叶级数与傅里叶变换_Part1_三角函数系的正交性
傅里叶级数与傅里叶变换_Part2_周期为2Π的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part3_周期为2L的函数展开为傅里叶级数
傅里叶级数与傅里叶变换_Part4_傅里叶级数的复数形式
傅里叶级数与傅里叶变换_Part5_傅里叶级数推导傅里叶变换
傅里叶级数与傅里叶变换_Part6_离散傅里叶变换推导
傅里叶级数与傅里叶变换_Part7_离散傅里叶变换的性质