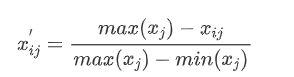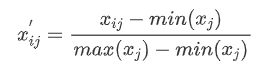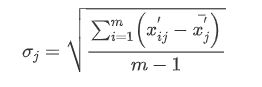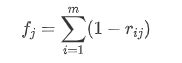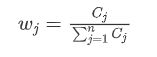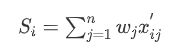【人因工程】熵值法与CRITIC法求权重
目录
前言
1. 熵值法定义
2. 熵值法公式
二、熵值法代码实现
三、CRITIC法理论
1. CRITIC法定义
2. CRITIC法公式
2.1 指标正向化及标准化
2.2 计算信息承载量
2.3 计算权重和评分
四、CRITIC法代码实现
五、二者对比
总结
前言
当需要求少量影响因素的权重时，不需要再用复杂的神经网络进行计算，只需要一些最基本的方法。具体分析见如下链接：
综合评价指标权重方法汇总 - 知乎 (zhihu.com)
https://zhuanlan.zhihu.com/p/342901550#:~:text=%E9%80%82%E7%94%A8%E5%9C%BA%E6%99%AF%EF%BC%9ACRITIC%E6%9D%83%E9%87%8D%E7%BB%BC%E5%90%88%E8%80%83%E8%99%91%E4%BA%86%E6%95%B0%E6%8D%AE%E6%B3%A2%E5%8A%A8%E6%83%85%E5%86%B5%E5%92%8C%E6%8C%87%E6%A0%87%E9%97%B4%E7%9A%84%E7%9B%B8%E5%85%B3%E6%80%A7%EF%BC%8C%E5%9B%A0%E6%AD%A4%EF%BC%8CCRITIC%E6%9D%83%E9%87%8D%E6%B3%95%E9%80%82%E7%94%A8%E4%BA%8E%E8%BF%99%E6%A0%B7%E4%B8%80%E7%B1%BB%E6%95%B0%E6%8D%AE%EF%BC%8C%E5%8D%B3%20%E6%95%B0%E6%8D%AE%E7%A8%B3%E5%AE%9A%E6%80%A7%E5%8F%AF%E8%A7%86%E4%BD%9C%E4%B8%80%E7%A7%8D%E4%BF%A1%E6%81%AF,%EF%BC%8C%20%E5%B9%B6%E4%B8%94%E5%88%86%E6%9E%90%E7%9A%84%E6%8C%87%E6%A0%87%E6%88%96%E5%9B%A0%E7%B4%A0%E4%B9%8B%E9%97%B4%E6%9C%89%E7%9D%80%E4%B8%80%E5%AE%9A%E7%9A%84%E5%85%B3%E8%81%94%E5%85%B3%E7%B3%BB%E6%97%B6%E3%80%82总结下来如笔记所示：
因此我们选用熵值法和CRITIC法求权重
一、熵值法理论
1. 熵值法定义
熵值法是计算指标权重的经典算法之一，它是指用来判断某个指标的离散程度的数学方法。离散程度越大，即信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。根据熵的特性，我们可以通过计算熵值来判断一个事件的随机性及无序程度，也可以用熵值来判断某个指标的离散程度，指标的离散程度越大，该指标对综合评价的影响越大。
2. 熵值法公式
1 .假设数据有n行记录，m个变量，数据可以用一个n*m的矩阵A表示(n行m列，即n行记录数，m个特征列)
2.数据的归一化处理
xij表示矩阵A的第i行j列元素。
3.计算第j项指标下第i个记录所占比重
4.计算第j项指标的熵值
5.计算第j项指标的差异系数
6.计算第j项指标的权重
二、熵值法代码实现
代码：
import numpy as np
#输入数据
loss = np.random.uniform(1, 4, size=5)
active_number = np.array([2, 4, 5, 3, 2])
data = np.array([loss, active_number])
print(data)
# 定义熵值法函数
def cal_weight(x):
'''熵值法计算变量的权重'''
# 正向化指标
#x = (x - np.max(x, axis=1).reshape((2, 1))) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
# 反向化指标
x = (np.max(x, axis=1).reshape((2, 1)) - x) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
#计算第i个研究对象某项指标的比重
Pij = x / np.sum(x, axis=1).reshape((2, 1))
ajs = []
#某项指标的熵值e
for i in Pij:
for j in i:
if j != 0:
a = j * np.log(j)
ajs.append(a)
else:
a = 0
ajs.append(a)
ajs = np.array(ajs).reshape((2, 5))
e = -(1 / np.log(5)) * np.sum(ajs, axis=1)
#计算差异系数
g = 1 - e
#给指标赋权，定义权重
w = g / np.sum(g, axis=0)
return w
w = cal_weight(data)
print(w)结果：
[[1.57242561 1.12780429 2.24411338 2.36236155 2.37789035]
[2. 4. 5. 3. 2. ]]
[0.70534397 0.29465603]
三、CRITIC法理论
1. CRITIC法定义
CRITIC是Diakoulaki（1995）提出一种评价指标客观赋权方法。该方法在对指标进行权重计算时围绕两个方面进行：对比度和矛盾（冲突）性。
它的基本思路是确定指标的客观权数以两个基本概念为基础。一是对比度，它表示同一指标各个评价方案取值差距的大小，以标准差的形式来表现，即标准化差的大小表明了在同一指标内各方案的取值差距的大小，标准差越大各方案的取值差距越大。二是评价指标之间的冲突性，指标之间的冲突性是以指标之间的相关性为基础，如两个指标之间具有较强的正相关，说明两个指标冲突性较低。
2. CRITIC法公式
2.1 指标正向化及标准化
设有m个待评对象，n个评价指标，可以构成数据矩阵X=（xij)m*n，设数据矩阵内元素，经过指标正向化处理过后的元素为xij'
- 若xj为负向指标（越小越优型指标）
- 若xj为正向指标（越大越优型指标）
2.2 计算信息承载量
-
对比性
用标准差表示第j 项指标的对比性
-
矛盾性
矛盾性反映的是不同指标之间的相关程度，若呈现显著正相关性，则矛盾性数值越小。设指标与其余指标矛盾性大小为fj
rij表示指标i 与指标j 之间的相关系数，在此使用的是皮尔逊相关系数，此为线性相关系数。
-
信息承载量
设指标与信息承载量为Cj
2.3 计算权重和评分
计算权重：
信息承载量越大可认为权重越大
计算得分：
四、CRITIC法代码实现
代码：
import numpy as np
#输入数据
loss = np.random.uniform(1, 4, size=5)
active_number = np.array([2, 4, 5, 3, 2])
data = np.array([loss, active_number])
print(data)
def CRITIC_weight(x):
#反向归一化
x = (np.max(x, axis=0) - x) / (np.max(x, axis=0) - np.min(x, axis=0))
#对比性
the = np.std(x, axis=0)
#矛盾性
#矩阵转置
data3 = list(map(list, zip(*x)))
r = np.corrcoef(data3) # 求皮尔逊相关系数
f = np.sum(1 - r, axis=1)
# 信息承载量
c = the * f
# 计算权重
w = c / np.sum(c, axis=0)
return w
x = data.T
w = CRITIC_weight(x)
print(w)结果：
[0.50785955 0.49214045]五、二者对比
代码：
#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
Created on Fri Mar 23 10:48:36 2018
@author: Big Teacher Brother
"""
import numpy as np
#输入数据
loss = np.random.uniform(1, 4, size=5)
active_number = np.array([2, 4, 5, 3, 2])
data = np.array([loss, active_number])
print(data)
# 定义熵值法函数
def cal_weight(x):
'''熵值法计算变量的权重'''
# 正向化指标
#x = (x - np.max(x, axis=1).reshape((2, 1))) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
# 反向化指标
x = (np.max(x, axis=1).reshape((2, 1)) - x) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
#计算第i个研究对象某项指标的比重
Pij = x / np.sum(x, axis=1).reshape((2, 1))
ajs = []
#某项指标的熵值e
for i in Pij:
for j in i:
if j != 0:
a = j * np.log(j)
ajs.append(a)
else:
a = 0
ajs.append(a)
ajs = np.array(ajs).reshape((2, 5))
e = -(1 / np.log(5)) * np.sum(ajs, axis=1)
#计算差异系数
g = 1 - e
#给指标赋权，定义权重
w = g / np.sum(g, axis=0)
return w
w = cal_weight(data)
print(w)
"""
# 定义熵值法函数
def cal_weight(x):
'''熵值法计算变量的权重'''
# 标准化
# 正向化指标
#x = (x - np.max(x, axis=1).reshape((2, 1))) / (np.max(x, axis=1).reshape((2, 1)) - np.min(x, axis=1).reshape((2, 1)))
# 反向化指标
x = (np.max(x, axis=0) - x) / (np.max(x, axis=0) - np.min(x, axis=0))
# 求k
k = 1.0 / math.log(5)
# 矩阵计算--
# 信息熵
# p=array(p)
x = array(x)
lnf = [[None] * 2 for i in range(5)]
lnf = array(lnf)
for i in range(0, 5):
for j in range(0, 2):
if x[i][j] == 0:
lnfij = 0.0
else:
p = x[i][j] / x.sum(axis=0)[j]
lnfij = math.log(p) * p * (-k)
lnf[i][j] = lnfij
lnf = pd.DataFrame(lnf)
E = lnf
# 计算冗余度
d = 1 - E.sum(axis=0)
# 计算各指标的权重
w = [[None] * 1 for i in range(cols)]
for j in range(0, cols):
wj = d[j] / sum(d)
w[j] = wj
# 计算各样本的综合得分,用最原始的数据
w = pd.DataFrame(w)
return w
if __name__ == '__main__':
# 计算df各字段的权重
w = cal_weight(data) # 调用cal_weight
w.index = data.columns
w.columns = ['weight']
print(w)
print('运行完成!')
"""
def CRITIC_weight(x):
#反向归一化
x = (np.max(x, axis=0) - x) / (np.max(x, axis=0) - np.min(x, axis=0))
#对比性
the = np.std(x, axis=0)
#矛盾性
#矩阵转置
data3 = list(map(list, zip(*x)))
r = np.corrcoef(data3) # 求皮尔逊相关系数
f = np.sum(1 - r, axis=1)
# 信息承载量
c = the * f
# 计算权重
w = c / np.sum(c, axis=0)
return w
x = data.T
w = CRITIC_weight(x)
print(w)结果：
[[1.57242561 1.12780429 2.24411338 2.36236155 2.37789035]
[2. 4. 5. 3. 2. ]]
[0.70534397 0.29465603]
[0.50785955 0.49214045]总结
可以看出两种方法的结果差异不大。