第十三届蓝桥杯C/C++省赛B组试题解析

一、AcWing 4402. 刷题统计

【题目描述】
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。
他计划周一至周五每天做$a$道题目，周六和周日每天做$b$道题目。
请你帮小明计算，按照计划他将在第几天实现做题数大于等于$n$题？

【输入格式】
输入一行包含三个整数$a,b$和$n$。

【输出格式】
输出一个整数代表天数。

【数据范围】
对于$50\%$的评测用例，$1\le a,b,n\le 10^6$。
对于$100\%$的评测用例，$1\le a,b,n\le 10^{18}$。

【输入样例】

10 20 99

【输出样例】

8

【分析】

---

每七天一循环，令$s=5a+2b$，表示一周可以刷的题数，那么$n/s$即为所需的周数，$n\%s$即为经过$n/s$周后还剩的题数，那么再模拟一下一周的七天即可。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
LL a, b, n, res;

int main()
{
    cin >> a >> b >> n;
    LL s = 5 * a + 2 * b;
    res = n / s * 7;
    n %= s;
    for (int i = 1; n > 0; i++, res++)
        if (i <= 5) n -= a;
        else n -= b;
    cout << res << endl;
    return 0;
}

二、AcWing 4403. 修剪灌木

【题目描述】
爱丽丝要完成一项修剪灌木的工作。
有$N$棵灌木整齐的从左到右排成一排。
爱丽丝在每天傍晚会修剪一棵灌木，让灌木的高度变为$0$厘米。
爱丽丝修剪灌木的顺序是从最左侧的灌木开始，每天向右修剪一棵灌木。
当修剪了最右侧的灌木后，她会调转方向，下一天开始向左修剪灌木。
直到修剪了最左的灌木后再次调转方向。
然后如此循环往复。
灌木每天从早上到傍晚会长高$1$厘米，而其余时间不会长高。
在第一天的早晨，所有灌木的高度都是$0$厘米。爱丽丝想知道每棵灌木最高长到多高。

【输入格式】
一个正整数$N$，含义如题面所述。

【输出格式】
输出$N$行，每行一个整数，第$i$行表示从左到右第$i$棵树最高能长到多高。

【数据范围】
对于$30\%$的数据，$N\le 10$。
对于$100\%$的数据，$1<N\le 10000$。

【输入样例】

3

【输出样例】

4
2
4

【分析】

---

对于第$i$棵树，有两种情况：第一种是从$i$的左边修剪到$i$，然后继续向右修剪，到右端点后再向左修剪到$i$，那么$i$长的高度为$2\ast (n-i)$；第二种是从$i$的右边修剪到$i$，然后继续向左修剪，到左端点后再向右修剪到$i$，那么$i$长的高度为$2\ast (i-1)$。

假设第一棵树的坐标为$1$，那么第$i$棵树能长的最大高度即为$max(i-1,n-i)\ast 2$。

---

【代码】

#include 
#include 
#include 
using namespace std;

int main()
{
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cout << max(i - 1, n - i) * 2 << endl;
    return 0;
}

三、AcWing 4404. X 进制减法

【题目描述】
进制规定了数字在数位上逢几进一。
X进制是一种很神奇的进制，因为其每一数位的进制并不固定！
例如说某种X进制数，最低数位为二进制，第二数位为十进制，第三数位为八进制，则X进制数$321$转换为十进制数为$65$。
现在有两个X进制表示的整数$A$和$B$，但是其具体每一数位的进制还不确定，只知道$A$和$B$是同一进制规则，且每一数位最高为$N$进制，最低为二进制。
请你算出$A-B$的结果最小可能是多少。
请注意，你需要保证$A$和$B$在X进制下都是合法的，即每一数位上的数字要小于其进制。

【输入格式】
第一行一个正整数$N$，含义如题面所述。
第二行一个正整数$M_a$，表示X进制数$A$的位数。
第三行$M_a$个用空格分开的整数，表示X进制数$A$按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数$M_b$，表示X进制数$B$的位数。
第五行$M_b$个用空格分开的整数，表示X进制数$B$按从高位到低位顺序各个数位上的数字在十进制下的表示。
请注意，输入中的所有数字都是十进制的。

【输出格式】
输出一行一个整数，表示X进制数$A-B$的结果的最小可能值转换为十进制后再模$1000000007$的结果。

【数据范围】
对于$30\%$的数据，$N\le 10$，$M_a,M_b\le 8$，$A\ge B$。
对于$100\%$的数据，$2\le N\le 1000$，$1\le M_a,M_b\le 100000$，$A\ge B$。

【输入样例】

11
3
10 4 0
3
1 2 0

【输出样例】

94

【样例解释】
当进制为：最低位$2$进制，第二数位$5$进制，第三数位$11$进制时，减法得到的差最小。
此时$A$在十进制下是$108$，$B$在十进制下是$14$，差值是$94$。

【分析】

---

假设$A,B$位数的最大值为$m$，不足$m$位的高位补零，即：$A=a_{m-1}{a}_{m-2}\dots a_0,B=b_{m-1}{b}_{m-2}\dots b_0$。再设每一位的进制分别为$p_{m-1},p_{m-2},\dots ,p_0$，则$A=a_{m-1}{\prod }_{i=0}^{m-2}{p}_i+a_{m-2}{\prod }_{i=0}^{m-3}+\cdots +a_0$，$B=b_{m-1}{\prod }_{i=0}^{m-2}{p}_i+b_{m-2}{\prod }_{i=0}^{m-3}+\cdots +b_0$。

设$a_i-b_i=d_i$，则$A-B=A=d_{m-1}{\prod }_{i=0}^{m-2}{p}_i+d_{m-2}{\prod }_{i=0}^{m-3}+\cdots +d_0$。对于$p_i$，只有第$i+1$位到第$m-1$位包括$p_i$，因此对所有包含$p_i$的项进行整理后得：$(d_{m-1}{\prod }_{k=i+1}^{m-2}{p}_k+d_{m-2}{\prod }_{k=i+1}^{m-3}{p}_k+\cdots +d_{i+1})\ast p_i\ast p_{i-1}\ast \cdots \ast p_0$。

显然$p_i\ast p_{i-1}\ast \cdots \ast p_0>0$，剩余的项为$A-B$的前缀（第$i+1$位到第$m-1$位），由于$A>B$，因此$A$的前缀一定大于等于$B$的前缀，所以上式的结果大于等于$0$，要使得结果尽可能小，则$p_i$应取最小值，即$max(a_i+1,b_i+1,2)$。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 100010, MOD = 1000000007;
int a[N], b[N];
int n, ma, mb, maxm;

int main()
{
    cin >> n >> ma;
    for (int i = ma - 1; i >= 0; i--) cin >> a[i];
    cin >> mb;
    for (int i = mb - 1; i >= 0; i--) cin >> b[i];
    maxm = max(ma, mb);
    int res = 0;
    for (int i = maxm - 1; i >= 0; i--)
        res = ((LL)res * max(a[i] + 1, max(b[i] + 1, 2)) + a[i] - b[i]) % MOD;
    cout << res << endl;
    return 0;
}

四、AcWing 4405. 统计子矩阵

【题目描述】
给定一个$N\times M$的矩阵$A$，请你统计有多少个子矩阵（最小$1\times 1$，最大$N\times M$）满足子矩阵中所有数的和不超过给定的整数$K$?

【输入格式】
第一行包含三个整数$N,M$和$K$。
之后$N$行每行包含$M$个整数，代表矩阵$A$。

【输出格式】
一个整数代表答案。

【数据范围】
对于$30\%$的数据，$N,M\le 20$。
对于$70\%$的数据，$N,M\le 100$。
对于$100\%$的数据，$1\le N,M\le 500$，$0\le A_{ij}\le 1000$，$1\le K\le 250000000$。

【输入样例】

3 4 10
1 2 3 4
5 6 7 8
9 10 11 12

【输出样例】

19

【样例解释】
满足条件的子矩阵一共有$19$，包含：

• 大小为$1\times 1$的有$10$个。
• 大小为$1\times 2$的有$3$个。
• 大小为$1\times 3$的有$2$个。
• 大小为$1\times 4$的有$1$个。
• 大小为$2\times 1$的有$3$个。

【分析】

---

本题如果使用二维前缀和做时间复杂度为$O(n^4)$，能过$70\%$的数据。如果使用一维前缀和与双指针做法，那么时间复杂度为$O(n^3)$。

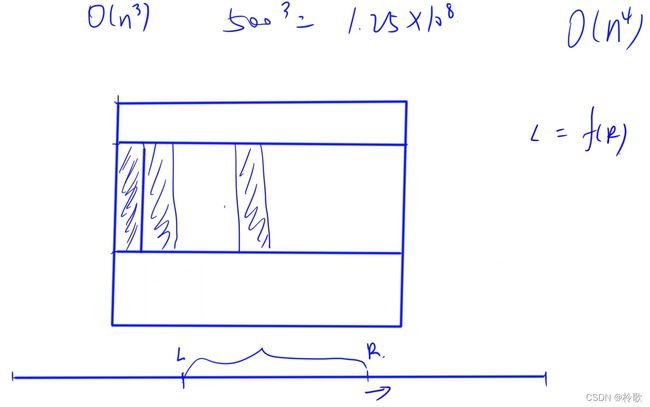
我们先预处理出$s[i][j]$表示第$j$列的前缀和，在枚举的时候我们只枚举行，将每一列的元素之和看成是一行中的一个数，假设当前枚举到第$i$行与第$j$行（$j\ge i$），如下图所示，然后我们再枚举矩形的右边界$r$，由于所有元素均为非负的，因此对于每一个$r$，满足区间和小于等于$k$的最小的矩形左边界$l$一定是随着$r$的增加而单调递增的，对于每个$r$，所能构造出的满足条件的子矩形即为$r-l+1$个。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 510;
int s[N][N];
int n, m, k;

int main()
{
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            cin >> s[i][j];
            s[i][j] += s[i - 1][j];
        }
    LL res = 0;
    for (int i = 1; i <= n; i++)
        for (int j = i; j <= n; j++)
            for (int r = 1, l = 1, sum = 0; r <= m; r++)
            {
                sum += s[j][r] - s[i - 1][r];
                while (sum > k) sum -= s[j][l] - s[i - 1][l], l++;
                res += r - l + 1;
            }
    cout << res << endl;
    return 0;
}

五、AcWing 4406. 积木画

【题目描述】
小明最近迷上了积木画，有这么两种类型的积木，分别为$I$型（大小为$2$个单位面积）和$L$型（大小为$3$个单位面积）：

同时，小明有一块面积大小为$2\times N$的画布，画布由$2\times N$个$1\times 1$区域构成。
小明需要用以上两种积木将画布拼满，他想知道总共有多少种不同的方式？
积木可以任意旋转，且画布的方向固定。

【输入格式】
输入一个整数$N$，表示画布大小。

【输出格式】
输出一个整数表示答案。
由于答案可能很大，所以输出其对$1000000007$取模后的值。

【数据范围】
$1\le N\le 10^7$

【输入样例】

3

【输出样例】

5

【样例解释】
五种情况如下图所示，颜色只是为了标识不同的积木：

【分析】

---

状态表示：$f[i][j]$表示已将前$i$列填满且填了第$i+1$列$j$个位置的方案数。

状态计算：

• 如果将第$i$列填满且填了第$i+1$列$0$个位置，那么有两种情况，一种是第$i$列竖着放了一个$I$型的积木，这样需要满足从第$i-1$列延伸出来的方块数量为$0$，即$f[i-1][0]$；另一种是第$i$列已经被从第$i-1$列延伸出来的方块占满了，即$f[i-1][2]$。
• 如果将第$i$列填满且填了第$i+1$列$1$个位置，那么有两种情况，一种是第$i$列放一个$L$型的积木且突出的那一块朝向第$i+1$列，有两种摆法，这样需要满足从第$i-1$列延伸出来的方块数量为$0$，即$2\ast f[i-1][0]$；另一种是第$i$列已经被第$i-1$列延伸出来的方块占了一个位置，那么在剩下的那个位置横着放一块$I$型的积木延伸到第$i+1$列，即$f[i-1][1]$。
• 如果将第$i$列填满且填了第$i+1$列$1$个位置，那么有两种情况，一种是第$i$列横着放两个$I$型的积木，这样需要满足从第$i-1$列延伸出来的方块数量为$0$，即$f[i-1][0]$；另一种是第$i$列已经被第$i-1$列延伸出来的方块占了一个位置，那么在剩下的那个位置放一块$L$型的积木，将第$i+1$列占满，即$f[i-1][1]$。

综上，状态转移方程为：

• $f[i][0]=f[i-1][0]+f[i-1][2]$；
• $f[i][1]=2\ast f[i-1][0]+f[i-1][1]$；
• $f[i][2]=f[i-1][0]+f[i-1][1]$。

初始化：第$1$列可以竖着放一个$I$型积木，有一种放法，即$f[1][0]=1$，可以放一个$L$型积木，有两种放法，即$f[1][1]=2$，可以横着放两个$I$型积木，有一种放法，即$f[1][2]=1$。

观察到每次状态转移只会涉及$i$和$i-1$两个状态，因此可以将$f$的第一维改为滚动数组。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int MOD = 1000000007;
int f[2][3];//f[i][j]表示已将前i列填满且填了第i+1列j个位置的方案数
int n;

int main()
{
    cin >> n;
    f[1][0] = 1;//第一列竖着放一个I型的
    f[1][1] = 2;//第一列放一个L型的，有一个方块突出到第i+1列
    f[1][2] = 1;//第一列横着放两个I型的
    for (int i = 2; i <= n; i++)
    {
        f[i & 1][0] = (f[i - 1 & 1][0] + f[i - 1 & 1][2]) % MOD;
        f[i & 1][1] = ((LL)f[i - 1 & 1][0] * 2 + f[i - 1 & 1][1]) % MOD;
        f[i & 1][2] = (f[i - 1 & 1][0] + f[i - 1 & 1][1]) % MOD;
    }
    cout << f[n & 1][0] << endl;
    return 0;
}

六、AcWing 4407. 扫雷

【题目描述】
小明最近迷上了一款名为《扫雷》的游戏。
其中有一个关卡的任务如下：
在一个二维平面上放置着$n$个炸雷，第$i$个炸雷$(x_i,y_i,r_i)$表示在坐标$(x_i,y_i)$处存在一个炸雷，它的爆炸范围是以半径为$r_i$的一个圆。
为了顺利通过这片土地，需要玩家进行排雷。
玩家可以发射$m$个排雷火箭，小明已经规划好了每个排雷火箭的发射方向，第$j$个排雷火箭$(x_j,y_j,r_j)$表示这个排雷火箭将会在$(x_j,y_j)$处爆炸，它的爆炸范围是以半径为$r_j$的一个圆，在其爆炸范围内的炸雷会被引爆。
同时，当炸雷被引爆时，在其爆炸范围内的炸雷也会被引爆。
现在小明想知道他这次共引爆了几颗炸雷？
你可以把炸雷和排雷火箭都视为平面上的一个点。
一个点处可以存在多个炸雷和排雷火箭。
当炸雷位于爆炸范围的边界上时也会被引爆。

【输入格式】
输入的第一行包含两个整数$n,m$。
接下来的$n$行，每行三个整数$x_i,y_i,r_i$，表示一个炸雷的信息。
再接下来的$m$行，每行三个整数$x_j,y_j,r_j$，表示一个排雷火箭的信息。

【输出格式】
输出一个整数表示答案。

【数据范围】
对于$40\%$的评测用例：$0\le x,y\le 10^9,0\le n,m\le 10^3,1\le r\le 10$。
对于$100\%$的评测用例：$0\le x,y\le 10^9,0\le n,m\le 5\times 10^4,1\le r\le 10$。

【输入样例】

2 1
2 2 4
4 4 2
0 0 5

【输出样例】

2

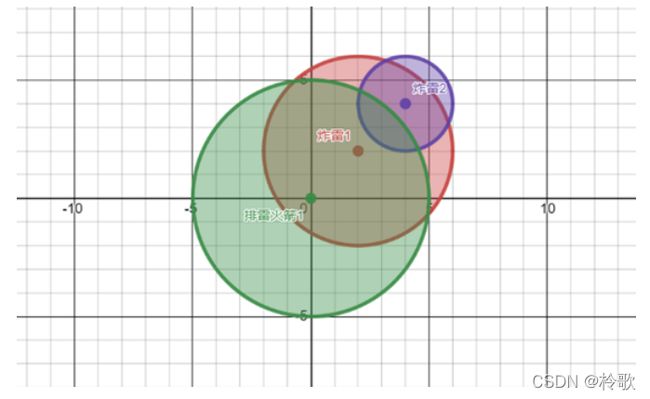
【样例解释】
示例图如下，排雷火箭$1$覆盖了炸雷$1$，所以炸雷$1$被排除；炸雷$1$又覆盖了炸雷$2$，所以炸雷$2$也被排除。

【分析】

---

首先可以将本题抽象成一个图论问题，如果排雷火箭或者炸雷$a$爆炸后能够炸到炸雷$b$，则连一条$a\to b$的有向边，所有的排雷火箭为起点，使用DFS或BFS遍历整个图求出能遍历到的炸雷的数量即为答案。由于是有向边，因此需要注意不能使用并查集求解。

本题的难点在于哈希，我们需要考虑怎么将这个图建出来，同一个点可能有多个炸雷。如果所有雷都在同一个点上，那么任意两点间都是有边的，对于$1\times 10^5$个点，就需要建$1\times 10^{10}$条边，会爆空间和时间。所以在做这题时最好不要把图建出来。

首先我们如何判断某个点炸了之后能炸到哪些点呢？肯定不能遍历所有炸雷，不然会TLE。由于所有点的半径不会超过$10$，因此每个点最多只会引爆三百多个点，那么我们可以直接枚举该点爆炸范围内的所有点，判断一下这个点上有没有炸雷。快速判断某个点有没有雷可以使用哈希表。

本题使用unordered_map无论存字符串还是存$longlong$都会被卡超时，因此我们需要手写一个哈希表。对于一个点$(x,y)$，可以使用公式$x\ast (10^9+1)+y$将其唯一地映射成一个$longlong$值，我们将其当做$hash$值。使用数组$h$将$hash$值转换成一个比较小的$int$值，表示某个点；使用数组$id$表示某个点对应的炸雷编号是多少，如果同一个点有多个炸雷，那么我们只记录爆炸半径最大的那个炸雷；使用数组$st$表示某个点是否被引爆过。最后我们通过$DFS$搜索出所有存在炸雷且会被引爆的点即可。

---

【代码】

#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 50010, M = 999997;//开十倍以上的点不易起冲突
LL h[M];
bool st[M];
int id[M];
int n, m;

struct Bomb//所有炸雷
{
    int x, y, r;
}bomb[N];

LL get_hash(int x, int y)
{
    return (LL)x * 1000000001 + y;
}

int find(int x, int y)
{
    LL hash = get_hash(x, y);
    int k = (hash % M + M) % M;
    while (h[k] != -1 && h[k] != hash)
        if (++k == M) k = 0;
    return k;
}

int square(int x)//手写平方函数比pow快很多
{
    return x * x;
}

void dfs(int x, int y, int r)
{
    st[find(x, y)] = true;
    for (int i = x - r; i <= x + r; i++)
        for (int j = y - r; j <= y + r; j++)
            if (square(i - x) + square(j - y) <= square(r))
            {
                int k = find(i, j);
                if (id[k] && !st[k]) dfs(i, j, bomb[id[k]].r);//如果炸雷爆炸范围内有炸雷且未被引爆则递归搜索
            }
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 1; i <= n; i++)
    {
        scanf("%d%d%d", &bomb[i].x, &bomb[i].y, &bomb[i].r);
        int k = find(bomb[i].x, bomb[i].y);
        if (h[k] == -1) h[k] = get_hash(bomb[i].x, bomb[i].y);//插入哈希表
        if (!id[k] || bomb[id[k]].r < bomb[i].r) id[k] = i;//这个位置没有炸雷或者原先炸雷的半径小于新炸雷的半径则更新
    }
    for (int i = 1; i <= m; i++)
    {
        int x, y, r;
        scanf("%d%d%d", &x, &y, &r);
        //由于不好遍历圆，可以遍历一个矩形，再判断该点是否在圆内
        for (int i = x - r; i <= x + r; i++)
            for (int j = y - r; j <= y + r; j++)
                if (square(i - x) + square(j - y) <= square(r))
                {
                    int k = find(i, j);
                    if (id[k] && !st[k]) dfs(i, j, bomb[id[k]].r);//如果排雷火箭半径范围内有炸雷且未被引爆则递归搜索
                }
    }
    int res = 0;//被引爆的炸雷的数量
    for (int i = 1; i <= n; i++)
        if (st[find(bomb[i].x, bomb[i].y)]) res++;
    printf("%d\n", res);
    return 0;
}

七、AcWing 4408. 李白打酒加强版

【题目描述】
话说大诗人李白，一生好饮。
幸好他从不开车。
一天，他提着酒壶，从家里出来，酒壶中有酒$2$斗。
他边走边唱：
无事街上走，提壶去打酒。
逢店加一倍，遇花喝一斗。
这一路上，他一共遇到店$N$次，遇到花$M$次。
已知最后一次遇到的是花，他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序，有多少种不同的可能？
注意：壶里没酒（$0$斗）时遇店是合法的，加倍后还是没酒；但是没酒时遇花是不合法的。

【输入格式】
第一行包含两个整数$N$和$M$。

【输出格式】
输出一个整数表示答案。由于答案可能很大，输出模$1000000007$的结果。

【数据范围】
对于$40\%$的评测用例：$1\le N,M\le 10$。
对于$100\%$的评测用例：$1\le N,M\le 100$。

【输入样例】

5 10

【输出样例】

14

【样例解释】
如果我们用$0$代表遇到花，$1$代表遇到店，$14$种顺序如下：

010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100

【分析】

---

状态表示：$f[i][j][k]$表示一共遇到$i$个店，$j$朵花，且有$k$斗酒的方案数。

状态计算：

• 如果最后遇到的为店，则上一个状态遇到的店的数量为$i-1$，花的数量为$j$，且有$k/2$斗酒，即$f[i][j][k]=f[i-1][j][k/2]$。需要满足$i>0$且$k\%2=0$；
• 如果最后遇到的为花，则上一个状态遇到的店的数量为$i$，花的数量为$j-1$，且有$k+1$斗酒，即$f[i][j][k]=f[i][j-1][k+1]$。需要满足$j>0$。

初始化：一个店和一朵花都还没遇到的时候有$2$斗酒的方案数为$1$，即$f[0][0][2]=1$。

由于最后一步的转移一定是唯一的，遇到花且将酒全部喝完，因此最后一个状态的前一个状态为遇到了$n$个店，$m-1$朵花，酒的数量为$1$斗，即$f[n][m-1][1]$。

---

【代码】

#include 
#include 
#include 
using namespace std;

const int N = 110, MOD = 1000000007;
int f[N][N][N];
int n, m;

int main()
{
    cin >> n >> m;
    f[0][0][2] = 1;
    for (int i = 0; i <= n; i++)
        for (int j = 0; j <= m; j++)
            for (int k = 0; k <= m; k++)
            {
                int &v = f[i][j][k];
                if (i && k % 2 == 0) v = (v + f[i - 1][j][k / 2]) % MOD;
                if (j) v = (v + f[i][j - 1][k + 1]) % MOD;
            }
    cout << f[n][m - 1][1] << endl;
    return 0;
}

八、AcWing 4409. 砍竹子

【题目描述】
这天，小明在砍竹子，他面前有$n$棵竹子排成一排，一开始第$i$棵竹子的高度为$h_i$。
他觉得一棵一棵砍太慢了，决定使用魔法来砍竹子。
魔法可以对连续的一段相同高度的竹子使用，假设这一段竹子的高度为$H$，那么使用一次魔法可以把这一段竹子的高度都变为 $\lfloor \sqrt{\lfloor H/2\rfloor +1}\rfloor$，其中$\lfloor x\rfloor$表示对$x$向下取整。
小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为$1$。

【输入格式】
第一行为一个正整数$n$，表示竹子的棵数。
第二行共$n$个空格分开的正整数$h_i$，表示每棵竹子的高度。

【输出格式】
一个整数表示答案。

【数据范围】
对于$20\%$的数据，保证$1\le n\le 1000,1\le h_i\le 10^6$。
对于$100\%$的数据，保证$1\le n\le 2\times 10^5,1\le h_i\le 10^{18}$。

【输入样例】

6
2 1 4 2 6 7

【输出样例】

5

【样例解释】
其中一种方案：

  2 1 4 2 6 7
→ 2 1 4 2 6 2
→ 2 1 4 2 2 2
→ 2 1 1 2 2 2
→ 1 1 1 2 2 2
→ 1 1 1 1 1 1

共需要$5$步完成。

【分析】

---

首先每棵竹子最多砍$6$次其高度就会变成$1$，因此我们可以先预处理出砍每棵竹子的高度变化过程，将初始高度记为最高层，每操作一次层数减一，高度为$1$是第$0$层，使用$f[i][j]$表示第$i$棵竹子第$j$层的高度，示意图如下图所示：

首先我们统计不考虑合并的情况下所有竹子砍到$1$所需的总步数$res$，并记下所有竹子中层数的最大值$m$。高度相同且相邻的竹子可以合并，而高度相同的情况只可能在同一层中出现。由于需要求最少操作次数，因此根据贪心的思想如果相邻的竹子高度相同那么一定要合并，所以我们可以先枚举每一层$j$，再枚举每一棵竹子$i$，如果$f[i][j]\ne 0$，即第$i$棵竹子在第$j$层是存在的，且$f[i][j]=f[i-1][j]$，即和前一棵竹子在这层的高度相同，那么就可以合并起来一起砍，总操作次数可以减一次，即$res--$。最后的$res$即为所需的最少的操作次数。

---

【代码】

#include 
#include 
#include 
#include 
using namespace std;

typedef long long LL;
const int N = 200010, M = 10;
LL stk[M], f[N][M];
int n, m, res;//m表示单个数需要操作的最大次数，res表示操作的总次数

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        LL x;
        cin >> x;
        int top = 0;
        while (x > 1) stk[++top] = x, x = sqrt(x / 2 + 1);
        res += top, m = max(m, top);
        for (int j = 0; top; j++, top--) f[i][j] = stk[top];
    }
    for (int j = 0; j < m; j++)
        for (int i = 1; i < n; i++)
            if (f[i][j] && f[i][j] == f[i - 1][j]) res--;
    cout << res << endl;
    return 0;
}