2019第十届蓝桥杯C/C++ 省赛A组 题解

A 平方和

2658417854
注意用long long

#include
using namespace std;

bool check(int a)
{
	for(;a;a=a/10)
	{
		int b=a%10;
		if(b==2||b==0||b==1||b==9)
			return true;
	}
	return false;
}

int main()
{
	long long int ans;
	for(int i=1;i<=2019;i++)
		if(check(i))
			ans+=(long long)i*i;
	cout<<ans;
	return 0;
}

B 数列求值

4659
因为结果要后四位，所以每个数都只留后四位，不会影响到后面的数

#include
using namespace std;

int a[21000000];

int main()
{
	a[1]=1;
	a[2]=1;
	a[3]=1;
	for(int i=4;i<=20200000;i++)
		a[i]=(a[i-1]+a[i-2]+a[i-3])%10000;
	cout<<a[20190324];
	return 0;
}

C 最大降雨量

34
7周的中位数的中位数，那么这个数在它所处的周有3个比它大，有3个周的中位数比它大，这3个周每周的中位数和中位数后的3个数比它大，那么最后就一共有3+3*4=15个数比它大，最大就是49-15=34

D 迷宫

数据没办法复制，就没运行程序。程序应该没问题，题中6**4的测试数据没问题，50*30的懒得打了
因为要求步数最少，就用bfs，按照步数的增长进行搜索，到达出口时，肯定是步数最少的。对于要求字典序最小，只需按照DLRU的顺序搜索即可。
题目还要求输出移动方向，那么还需要一个数组记录到达每一块的上一块的位置，因为需要最小步数，所以说每块的上一块的位置是唯一的。为了输出方便，从终点开始，搜索起点。如果是反序的话，注意搜索的顺序就要改变，因为方向变了，正序的D是向下，那么反序的D就是向上了。我是懒得改了，就把加号改成减号了，一样都是相反的。

#include
#include
using namespace std;

const int xx[]={1,0,0,-1};
const int yy[]={0,-1,1,0};
const char dir[]={'D','L','R','U'};
int map[55][35];
int vis[55][35];
struct next
{
	char d;
	int nox,noy;
}nxt[55][35];
int n,m;
struct node
{
	int x,y;
};
queue<node>save;

void bfs()
{
	node tmp;
	tmp.x=n;
	tmp.y=m;
	vis[n][m]=1;
	save.push(tmp);
	while(save.size())
	{
		tmp=save.front();
		save.pop();
		for(int i=0;i<4;i++)
		{
			int dx=tmp.x-xx[i];
			int dy=tmp.y-yy[i];
			if(dx>n||dx<1||dy>m||dy<1||vis[dx][dy]||map[dx][dy])
				continue;
			nxt[dx][dy].d=dir[i];
			nxt[dx][dy].nox=tmp.x;
			nxt[dx][dy].noy=tmp.y;
			vis[dx][dy]=1;
			node t;
			t.x=dx;t.y=dy;
			save.push(t);
			if(dx==1&&dy==1)
				return;
		}
	}
}

int main()
{
	n=50,m=30;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			cin>>map[i][j];
	bfs();
	int x=1,y=1;
	while(1)
	{
		cout<<nxt[x][y].d;
		int a=nxt[x][y].nox,b=nxt[x][y].noy;
		x=a;
		y=b;
		if(x==n&&y==m)
			break;
	}
	return 0;
}

E RSA解密

我的想法是因为n是两个质数相乘的结果，所有n的因子除1和本身只有p和q，先用欧拉筛，找到一定数量的质数，n可以整除的那个就为p，另外一个就是q，我的欧拉筛数组开到1000000001还是没有找到，开到2000000001就跑不出来了，运行内存占用从百分之二十几一下跳到百分之九十九。如果有了p和q再用一个循环去找e，最后用快速幂。可p和q就找不出来，╮(╯﹏╰）╭。

#include
using namespace std;

int *pri=new int[10000001];
int *check=new int[1000000001];
int cnt;

void euler(long long int n)
{
	for(int i=2;i<=n;i++)
	{
		if(!check[i])
			pri[++cnt]=i;
		for(int j=1;pri[j]*i<=n;j++)
		{
			check[pri[j]*i]=1;
			if(i%pri[j]==0)
				break;
		}
	}
}

int main()
{
	euler(2000000001);
	long long int n=1001733993063167141;
	long long int p,q;
	int i;
	for(i=1;i<=cnt;i++)
		if(n%pri[i]==0)
			break;
	p=pri[i];
	q=n/p;
	cout<<p<<endl<<q;
	return 0;
}

人傻了，用什么素数筛，直接暴力不就好了，反正时间不限
呃呃呃，两个小时没跑出来，放弃了

F 完全二叉树的权值

题目比较简单
两个注意的地方：首先是最后一行不满，注意不要数组越界。还有可能每一行的和为负数，所以最大值要初始为一个比较小的数

#include
#include
using namespace std;

int a[100005];
long int d[105];

int main()
{
	int n;
	cin>>n;
	int h=log(n)/log(2);
	if(n>pow(2,h)-1)
		h++;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	long int mmax=-1e10,mmaxd=-1;			//可能所有和是负数 
	for(int i=1;i<=h;i++)
	{
		int m=pow(2,i-1);
		int e=m+m-1;
		if(e>n)
			e=n;							//注意最后一行可能不满  避免越界 
		for(int j=m;j<=e;j++)
			d[i]+=a[j];
		if(d[i]>mmax)
		{
			mmax=d[i];
			mmaxd=i;
		}
	}
	cout<<mmaxd;
	return 0;
}

G 外卖店优先级

我的代码只能过百分之八十的数据。我还看了一下别人的博客。
先说一下我的想法。题中的输入的订单时间是没有按顺序的，首先先排一下顺序。对每一个时间单位，之前已经排序，读取当前时间的订单，将该时间的订单所有店铺加二，并标记，对于没有标记的大于0的都减一。注意是小于等于3才清楚，不是小于5。代码中注释很详细

#include
#include
#include
#include 
using namespace std;

struct Order
{
	int t,no;
}order[100001];
int shop[100001];
bool vis[100001];
int pri[100001];


bool cmp(const Order a,const Order b)
{
	return a.t<b.t;
}

int main()
{
	int n,m,t;
	cin>>n>>m>>t;
	for(int i=1;i<=m;i++)
		scanf("%d%d",&order[i].t,&order[i].no); 
	sort(order+1,order+m+1,cmp);									//排序 
	int cnt=1;
	for(int i=1;i<=m;)
	{
		if(order[i].t==cnt)											//同一个时间 
		{
			vis[order[i].no]=1;										//标记 
			shop[order[i].no]+=2;									//加2 
			i++;													//下一个订单 
		}
		else														//不是同一个时间 
		{
			cnt++;
			for(int j=1;j<=n;j++)									//对上一个时间的店铺进行处理 
			{
				if(shop[j]&&!vis[j])								//未标记且大于0的减1 
					shop[j]--;
				if(cnt>=t-2) 										//只有最后两轮可以决定优先的店铺   减少运行的时间 
				{
					if(shop[j]>5)									//加入 
						pri[j]=1;
					else if(shop[j]<=3)								//去除 
						pri[j]=0;
				}
			}
			memset(vis,0,sizeof(vis));								//标记重置 
		}
	}
	if(order[m].t==cnt)												//因为每一次都是处理上一轮  可能循环退出时，最后一轮为处理 
		for(int j=1;j<=n;j++)
		{
			if(shop[j]&&!vis[j])
				shop[j]--;
			if(shop[j]>5)
				pri[j]=1;
			else if(shop[j]<=3)
				pri[j]=0;
		}
	while(cnt<t)													//最后一个订单的时间，小于总时间 
	{
		cnt++;
		for(int j=1;j<=n;j++)
		{
			shop[j]--;
			if(shop[j]>5)
				pri[j]=1;
			else if(shop[j]<=3)
				pri[j]=0;
		}
	}
	int tot=0;
	for(int j=1;j<=n;j++)
		if(pri[j])
			tot++;
	cout<<tot;
	return 0;
}

参考别人的，感觉比我的强好多，本蒟蒻还需要努力学习！排序是按照时间和店号排序。这样相同的一个店相同时间的订单一块处理，同时记录每一个店上次有订单的时间，下一次订单的时间减去上一次订单的时间就是中间没有订单的时间。详细见注释

#include
#include
#include
#include 
using namespace std;

struct Order
{
	int t,no;
}order[100001];											//订单											 
int shop[100001];										// 优先级 
int last[100001];										//上一次订单的时间	
int pri[100001];										//是否优先 


bool cmp(const Order a,const Order b)
{
	if(a.t!=b.t) 
		return a.t<b.t;
	return a.no<b.no;
}

int main()
{
	int n,m,t;
	cin>>n>>m>>t;
	for(int i=1;i<=m;i++)
		scanf("%d%d",&order[i].t,&order[i].no); 
	sort(order+1,order+m+1,cmp);						//排序 
	for(int i=1;i<=m;)
	{
		int j=i;
		while(order[i].t==order[j+1].t&&order[i].no==order[j+1].no&&j<m)
			j++;										//有多少个相同订单 
		int ot=order[i].t,ono=order[i].no,cnt=j-i+1;
		shop[ono]-=ot-last[ono]-1;						//此处时间减去上次时间+1  之间没有订单的时间，优先级减1 
		if(shop[ono]<0)
			shop[ono]=0;
		if(shop[ono]<=3)								//清除 
			pri[ono]=0;
		shop[ono]+=cnt*2;								//订单优先级增加 
		if(shop[ono]>5)	
			pri[ono]=1;									//加入 
		last[ono]=ot;									//更新最后一个订单时间 
		i=++j;											
	}
	for(int i=1;i<=n;i++)
	{
		shop[i]-=t-last[i];								//t-最后的时间 
		if(shop[i]<=3)
			pri[i]=0;
	}
	int tot=0;
	for(int i=1;i<=n;i++)
		if(pri[i])
			tot++;
	cout<<tot; 
	return 0;
}

H 修改数组

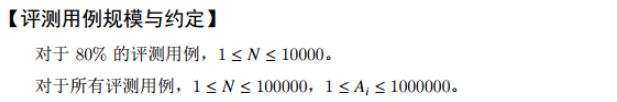
一看题感觉很简单，再看数据范围，发现蒟蒻又只能过百分之八十的数据

#include
#include
using namespace std;

int w[100005];
int a[100005];

int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		if(!w[a[i]])
			w[a[i]]++;
		else
		{
			while(w[++a[i]]);
			w[a[i]]++;
		}
		printf("%d ",a[i]);
	}
	return 0;
}
}

又想了想，可以用并查集做。刚开始所有的父节点都指向自己，如果一个结点的父节点指向自己，就说明这个结点代表的数没有用过，就可以用，然后因为这个数用过了，再把父节点加1，如果又遇到相同的这个点，此时该结点的父节点不指向自己，而是自己的值加1，那么继续查找加1是不是指向自己，如果还不是，继续查找加1的父节点的父节点是不是指向自己，一直找下去，直到遇到指向自己的，这个点用完后父节点加1。注意还有压缩路径，就是将刚才的所有途径的点的父节点都设为最后那个点。

#include
#include
using namespace std;

int fa[1000005];

int getfa(int x)
{
	if(x==fa[x])
	{
		fa[x]++;
		return x;
	}
	return fa[x]=getfa(fa[x]);
}

int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=1000005;i++)
		fa[i]=i;
	for(int i=1;i<=n;i++)
	{
		int a;
		scanf("%d",&a);
		printf("%d ",getfa(a));
	}
	return 0;
}

I 糖果

n小于二十，可以直接枚举。大于二十，还没什么想法。

#include
#include
#include
using namespace std;

int w[101][21];

int main()
{
	int n,m,k;
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=k;j++)
			cin>>w[i][j];
	int sum=0;
	for(int i=1;i<=m;i++)
		sum^=i;
	int l=1<<(n-1);
	int minn=105;
	for(int i=1;i<=l;i++)
	{
		int j=i,tmp=sum,cnt=0;
		for(int q=0;q<n;q++)
		{
			int t=1<<q;
			if(j&t)
			{
				for(int p=1;p<=3;p++)
					tmp^=w[q+1][p];
				cnt++;
			}
		}
		if(!tmp)
			minn=min(minn,cnt);cout<<i<<endl;
	}
	if(minn>n)
		cout<<"-1";
	else
		cout<<minn;
	return 0;
}

J 组合数问题