【机器学习】机器学习基本概念/术语3
上一篇:机器学习的基本概念/术语2
序言
记录机器学习基本概念,不做详细解释,常识积累。长期更新…
# 线性回归
-
Linear Regression,是回归问题的基础
-
什么是"线性":直线方程y = kx+b是线性方程,机器学习中指两个变量间的线性相关性,”线性”限制的是参数parameter而不是特征feature(自变量),因为一般特征x是已知的,我们关心的是参数w和b
-
什么是"回归":regression,与回归相对的是分类问题(classification),分类问题要预测的变量y输出集合是有限的,预测值只能是有限集合内的一个。当要预测的变量y输出集合是无限且连续,我们称之为回归。比如,天气预报预测明天是否下雨,是一个二分类问题;预测明天的降雨量多少,就是一个回归问题。回归问题也可以转换为分类问题
-
线性回归要做的是就是找到一个数学公式能相对较完美地把所有自变量线性组合起来,得到的结果和目标接近
-
最简单的线性回归是一元线性回归,也就是只有一个特征的时候,如果特征超过一个那就是多元线性回归。
-
与线性回归对应的是非线性回归,比如多项式回归、逻辑回归、SVM等
-
做线性回归,不要忘了前提假设是y和x呈线性关系,如果两者不是线性关系,就要选用其他模型了
# 逻辑回归
- Logistic Regression,逻辑回归又叫"对数几率回归",名字是回归,实际却是一种分类学习方法
- 它的原理是利用逻辑函数把线性回归的结果(-无穷,+无穷)映射到(0,1)
- 逻辑函数如下,把线性回归的结果放到逻辑函数中就构造了逻辑回归函数
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z} } g(z)=1+e−z1
- 通过极大似然函数来估计参数w和b,使用对数似然将连乘变成加法,而且对数似然函数的损失函数是关于未知参数的高阶可导连续凸函数,使用梯度下降法、牛顿法等都可以求解其最优解
- 如果取整个数据集上的平均对数似然损失作为损失函数(对数似然前添加负号取平均得到) ,在逻辑回归中最大化似然函数和最小化损失函数是等价的
J ( θ ) = − 1 m l n ( L ( θ ) ) J(\theta )=-\frac{1}{m}ln(L(\theta )) J(θ)=−m1ln(L(θ))
# 生成模型/判别模型
-
判别模型Discriminative Model,直接学习决策函数 f ( x ) f(x) f(x)或条件概率分布 P ( y ∣ x ) P(y|x) P(y∣x)作为预测的模型;判别模型关心的是对给定输入 x x x,应该输入预测什么样的输出 y y y
-
比如要确定一只羊是山羊还是绵羊,用判别模型的方法是先从历史数据中学习到模型,然后通过提取这只羊的特征来预测出这只羊是绵羊的概率、是山羊的概率
-
生成模型Generative Model,由数据学习输入和输出的联合概率 P ( x , y ) P(x,y) P(x,y),然后通过贝叶斯定理求出后验概率分布 P ( y ∣ x ) P(y|x) P(y∣x)作为预测的模型
-
用生成模型的方法:根据山羊特征学习出一个山羊模型,然后根据绵羊的特征学习出一个绵羊模型。然后从这只羊提取特征,放到山羊模型中看概率是多少,再放到绵羊模型中看概率是多少,哪个大就是哪个
-
总结:生成模型和判别模型都是使后验概率 P ( y ∣ x ) P(y|x) P(y∣x)最大化。判别式是直接对后验概率建模,而生成式模型通过贝叶斯定理这一"桥梁"使问题转化为求联合概率,因此生成式模型可以体现更多数据本身的分布信息,其普适性更广;生成模型可以转化为判别模型,但判别模型不能转化为生成模型,二者训练阶段的目的不一样
# 低密度区和高密度区
-
密度聚类中的概念
-
密度:以空间中的一个样本为中心,单位体积内的样本个数称为该点的密度。
-
DBSCAN:Density-Based Spatial Clustering of Applications with Noise是一种著名的密度聚类算法,它基于一组邻域参数来刻画样本分布的紧密程度。DBSCAN先发现密度较高的点,然后把相近的高密度点逐步连成一片,进而生成各种簇
-
简单熟悉几个密度聚类相关的概念:
核心对象:邻域内至少包含min points个样本的对象,邻域和min points个数均可指定
密度直达:两个样本位于同一邻域内,且其中一个样本是核心对象,称样本由核心对象密度直达密度可达:两个样本能由密度直达串起来,称样本由核心对象密度可达
密度相连:若两个样本均由另一个样本密度可达,称这两个样本密度相连
# K-means clustering
-
k均值聚类算法,在上一篇博客中有介绍过,该方法又称老大法,是一种无监督学习方法,分类是事先知道所要得到的类别,而聚类则不一样,只能以相似度为基础,将对象分为不同的簇
-
k均值算法的步骤:
(1) 选取数据空间中的K个对象作为初始中心,每个对象代表一个聚类中心
(2) 对于样本中的数据对象,根据它们与这些聚类中心的欧氏距离,按距离最近的准则将它们分到距离它们最近的聚类中心(最相似)所对应的类
(3) 更新聚类中心:将每个类别中所有对象所对应的均值作为该类别的聚类中心,计算目标函数的值;聚类的目标是各类的聚类平方和最小(欧氏距离作为相似度指标)
(4) 重复(2)和(3)直到代价函数收敛,(2)中固定簇中心使代价函数减小,(3)中更新簇中心使代价函数进一步减小,并交替进行直至收敛 -
k均值算法的缺点:
(1) 需要人工预先确定初始k值,且该值和真实的数据分布未必吻合
(2) k均值只能收敛到局部最优,效果受到初始值很大
(3) 易受到噪点的影响
(4) 样本点只能被划分到单一的类中 -
k均值算法的优点:
对于大数据集, k均值聚类算法相对是可伸缩和高效的,它的计算复杂度是 O(NKt) 接近于线性,其中N是数据对象的数目,k是聚类的簇数,t是迭代的轮数。尽管算法经常以局部最优结束 , 但一般情况下达到的局部最优已经可以满足聚类的需求
# 消融研究
- ablation study
- 消融研究通常指删除模型或算法的某些功能,并查看其如何影响性能
- 论文提出的模型可能包含多个结构模块,这些模块均为模型的性能做出了贡献,为了了解每部分单独发挥的作用,常常在论文中提出消融研究;简单说就是通过对照组来证明模块的必要性
# 变分
- Calculus of Variations
- 变分就是求泛函的极值,泛函就是函数的函数,以函数为自变量,以实数或复数为函数值的特殊函数。比如曲线长度、沿路径做功消耗的能量等
- 泛函的极值
F y ′ = δ F δ y = lim y 2 → y 1 F ( y 2 ) − F ( y 1 ) y 2 − y 1 F^{'}_{y} = \frac{\delta F}{\delta y} =\lim_{y_{2} \to y_{1} }\frac{F(y_{2} )-F(y_{1} ) }{y_{2}-y_{1}} Fy′=δyδF=y2→y1limy2−y1F(y2)−F(y1)
δ I = ∫ a b f ′ ( y ) δ y d x \delta I =\int_{a}^{b} f^{'}(y)\delta ydx δI=∫abf′(y)δydx
- δ y \delta y δy的定义 δ y : = lim y 1 → y 2 ( y 2 − y 1 ) \delta y:=\lim_{y_{1} \to y_{2} }(y_{2}-y_{1}) δy:=limy1→y2(y2−y1),可见 δ y \delta y δy也是 x x x的函数,更确切的记法是 δ y ( x ) \delta y(x) δy(x),不一定是常量
- f ′ ( y ) = 0 f^{'}(y)=0 f′(y)=0能保证 I I I处在极值状态
# 重参数化
-
reparameterization trick
-
VAE中 q ( z ∣ x ) q(z|x) q(z∣x)的分布可以通过以下两步来表达:
(1) 先从标准正态分布中采样一个噪声变量 ε ε ε, ε ∼ p ( ϵ ) \varepsilon \sim p(\epsilon ) ε∼p(ϵ),用来保持 z z z随机性
(2) 然后使用确定性变换 g ( ε , x ) g(ε, x) g(ε,x)把随机噪声映射到更复杂的分布上 z = g ( ε , x ) z = g(ε,x) z=g(ε,x) -
高斯分布提供了最简单的重参数化技巧, z ∼ N ( μ , σ ) z \sim N(\mu ,\sigma ) z∼N(μ,σ),可以写成
z = g μ , σ ( ϵ ) = μ + ϵ ∗ σ , u ∼ N ( 0 , 1 ) z=g_{\mu ,\sigma } (\epsilon )=\mu +\epsilon *\sigma ,u\sim N(0,1) z=gμ,σ(ϵ)=μ+ϵ∗σ,u∼N(0,1),两种方式得到的z都服从相同分布; -
我们就能看到采样结果和z之间的关系,也能求出有效的梯度。这样的话,期望的梯度可以表达为:
∇ ϕ E z ∼ q ϕ ( z ∣ x ) [ f ( x , z ) ] = ∇ ϕ E ϵ ∼ p ( ϵ ) [ f ( x , g ϕ ( ϵ , x ) ) ] = E ϵ ∼ p ( ϵ ) [ ∇ ϕ f ( x , ) g ϕ ( ϵ , x ) ) ] \begin{aligned} \nabla _{\phi } E_{z\sim q_{\phi } (z|x)} \left [ f(x,z) \right ] &=\nabla _{\phi }E_{\epsilon \sim p (\epsilon )}\left [ f(x,g_{_{\phi } }(\epsilon ,x) ) \right ] \\ &=E_{\epsilon \sim p (\epsilon )}\left [\nabla _{\phi }f(x,) g_{_{\phi } }(\epsilon ,x)) \right ] \end{aligned} ∇ϕEz∼qϕ(z∣x)[f(x,z)]=∇ϕEϵ∼p(ϵ)[f(x,gϕ(ϵ,x))]=Eϵ∼p(ϵ)[∇ϕf(x,)gϕ(ϵ,x))]
梯度转换到了期望内部,可以采用Monte Carlo采样来评估
# Checkpoint
- checkpoint用于在模型训练的过程中保存模型训练现场,不仅保存模型的参数、优化器参数,还有epoch、loss等,相当于一个保存模型的文件夹
- 可用于训练后推理或再训练场景:
训练后推理:训练过程中通过实时验证精度,把精度最高的模型参数保存下来用于预测
再训练场景:长时间训练保存ckpt防止任务异常退出丢失进度;Fine-tune场景基于ckpt面向第二个类似任务进行模型训练
# 数据泄露
-
Data Leakage
-
数据泄露包含两个条件:(1)训练的特征数据泄露了目标的信息;(2)泄露了信息的特征数据往往在模型实际预测时,无法获得
-
理解:比如知道了测试数据的未来位置信息用于训练,而模型实际预测时是不知道未来位置信息的;或者比如开发一个用来诊断特定疾病的模型,训练集中包含了病人是否因为该疾病做过手术(间接泄露了疾病信息)的特征,使用该特征可以极大提高预测准确性,但这种把关联结果当作特征用于训练,明显存在数据泄露,因为这个特征在诊断疾病结果出来之前是无法知道的,结果出来之后倒是可以对比是否因疾病做过手术
-
影响:数据泄露会导致模型在训练、评估时的正确率很高,而在实际使用过程中正确率很低
-
分类:数据泄露问题一般可以分为两类,target leakage(如上定义,特征泄露了目标信息);train-test contamination(训练集和测试集的交叉污染)
-
检查是否发生了数据泄露:
(1) 训练和实际测试差别很大(当然也可能是过拟合或其他原因);
(2) 特征-结果相关分析
(3) 有限部署后看差别 -
修复数据泄露:
(1) 训练时使用训练集而非整个数据集;
(2) 时间序列问题避免出现未来信息;
(3) 剔除结果高度相关的特征
# 隐变量
- Latent Variable
- 比如VAE中的隐变量z,VAE网络结构:推断网络->z->生成网络
- z是不可直接观测的综合变量,可认为是隐藏层数据
# ELBO
- ELBO = Evidence Lower Bound,证据下界
- 证据:数据或者可观测变量的概率密度。假设 x x x是可观测数据集, z z z是隐变量, p ( z , x ) p(z,x) p(z,x)是联合概率, p ( z ∣ x ) p(z|x) p(z∣x)条件概率,p(x)为证据
- 贝叶斯条件概率 p ( z ∣ x ) = p ( z , x ) / p ( x ) p(z|x) = p(z,x) / p(x) p(z∣x)=p(z,x)/p(x),对很多模型来说计算 p ( x ) p(x) p(x)是困难的,即 p ( x ) = ∫ p ( z , x ) d z p(x)=\int p(z,x)dz p(x)=∫p(z,x)dz。由于无法直接计算条件概率/后验概率分布 p ( z ∣ x ) p(z|x) p(z∣x),使用变分推断,变分推断的目标就是用一个概率密度函数 q ( z ) q(z) q(z)来近似 p ( z ∣ x ) p(z|x) p(z∣x),要得到最佳的 q ( z ) q(z) q(z),必须优化
q ∗ ( z ) = a r g m i n [ K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) ] q^{*} (z)=argmin \left [ KL(q(z) || p(z|x) ) \right ] q∗(z)=argmin[KL(q(z)∣∣p(z∣x))]其中KL散度可以表示为
K L ( q ( z ) ∣ ∣ p ( z ∣ x ) ) = E [ l o g ( q ( z ) ) ] − E [ l o g ( p ( z , x ) ) ] + l o g ( p ( x ) ) KL(q(z) || p(z|x) ) =E[log(q(z))]-E[log(p(z,x))]+log(p(x)) KL(q(z)∣∣p(z∣x))=E[log(q(z))]−E[log(p(z,x))]+log(p(x))由于KL散度大于等于0,我们得到
l o g ( p ( x ) ) ≥ E [ l o g ( p ( z , x ) ) ] − E [ l o g ( q ( z ) ) ] log(p(x))\ge E[log(p(z,x))]-E[log(q(z))] log(p(x))≥E[log(p(z,x))]−E[log(q(z))]这个就是证据下界,左边是证据的对数形式,右边为其下界。因此我们有
E L B O ( q ) = E [ l o g ( p ( z , x ) ) ] − E [ l o g ( q ( z ) ) ] ELBO(q)= E[log(p(z,x))]-E[log(q(z))] ELBO(q)=E[log(p(z,x))]−E[log(q(z))]在变分推断时首先需要计算的便是 E L B O ELBO ELBO,要计算 E L B O ELBO ELBO,需要写出联合概率密度 p ( x , z ) p(x, z) p(x,z)和 q ( z ) q(z) q(z),然后带入 E L B O ( q ) ELBO(q) ELBO(q)分别求对数,之后分别求期望,然后针对具体的变分参数求偏导,并令偏导等于0,即可得到变分参数的更新公式
# FPV
- First Person View,第一人称主视角,无人机领域;
- 也可表示自车和行人交互时自车视角
# MAE = L1 Loss
- Mean Absolute Error,平均绝对误差,表示预测值和观测值之间绝对误差的平均值
M A E = ∑ i = 1 n ∣ y i − x i ∣ n MAE = \frac{ {\textstyle \sum_{i=1}^{n}}\left | y_{i}-x_{i} \right | }{n} MAE=n∑i=1n∣yi−xi∣
# MSE = L2 Loss
- Mean Squared Error,均方误差,表示预测值与观测值的差的平方之和求平均
M S E = S S E n = 1 n ∑ i = 1 m ω i ( y i − y i ^ ) 2 MSE=\frac{SSE}{n} =\frac{1}{n} \sum_{i=1}^{m}\omega _{i}(y_{i}-\hat{y_{i}} ) ^{2} MSE=nSSE=n1i=1∑mωi(yi−yi^)2 - SSE = Sum of Squared Error,误差平方和
# RMSE
- Root Mean Squared Error,均方根误差
- MSE开根号,用于数据的更好描述
R M S E = M S E = S S E n = 1 n ∑ i = 1 m ω i ( y i − y i ^ ) 2 RMSE = \sqrt{MSE} =\sqrt{\frac{SSE}{n}} =\sqrt{\frac{1}{n} \sum_{i=1}^{m}\omega _{i}(y_{i}-\hat{y_{i}} ) ^{2} } RMSE=MSE=nSSE=n1i=1∑mωi(yi−yi^)2
# GT/TP/TN/FP/FN
- GT = Ground Truth,真值;TP/FP/TN/FN都是模型预测的结果
- TP = True Positive,GT是Positive且预测为Positive,模型预测正确的正样本
- FN = False Negative,GT是Positive但预测为Negative,模型预测错误的正样本
- TN = True Negative,GT是Negative且预测为Negative,模型预测正确的负样本
- FP = False Positive,GT是Negative但预测为Positive,模型预测错误的负样本
# Recall
- 召回率/查全率
- 召回率表示某一类样本预测正确的与所有真值GT的比例
R e c a l l = T P T P + F N Recall = \frac{TP}{TP+FN} Recall=TP+FNTP
# Precision
- 精确率/查准率
- 表示某一类样本预测有多准
P r e c i s i o n = T P T P + F P Precision = \frac{TP}{TP + FP} Precision=TP+FPTP
# Accuracy
- 准确率
- 预测正确的样本比例,一般指预测正确的正样本
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy = \frac{TP + TN}{TP + TN + FP + FN} Accuracy=TP+TN+FP+FNTP+TN
# F-Score
- 精确率和召回率互相影响,理想状态下肯定追求两个都高,但是实际情况是两者相互"制约":追求精确率高,则召回率就低;追求召回率高,则通常会影响精确率
- 我们当然希望预测的结果精确率越高越好,召回率越高越好,但事实上这两者在某些情况下是矛盾的,引入F-Score作为综合指标平衡精确率和召回率的影响
F s c o r e = ( 1 + β 2 ) P r e c i s i o n ∗ R e c a l l β 2 ∗ P r e c i s i o n + R e c a l l F_{score} =(1+\beta ^{2} )\frac{Precision*Recall}{\beta ^{2}*Precision+Recall} Fscore=(1+β2)β2∗Precision+RecallPrecision∗Recall
- β β β如果取1,表示 P r e c i s i o n Precision Precision与 R e c a l l Recall Recall一样重要
β β β如果取小于1,表示 P r e c i s i o n Precision Precision比 R e c a l l Recall Recall重要
β β β如果取大于1,表示 R e c a l l Recall Recall比 P r e c i s i o n Precision Precision重要
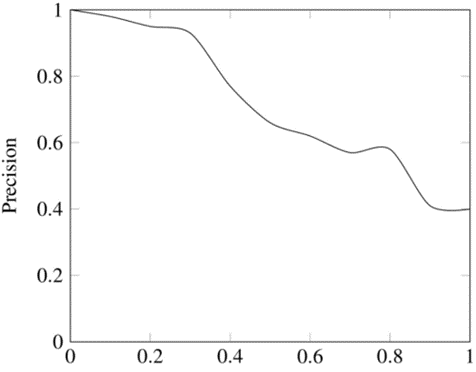
# PR曲线
- Precision-Recall Curve
-
以召回率Recall Rate作为横坐标轴,精确率Precision Rate作为纵坐标轴
-
预测轨迹召回率:预测了n个目标,命中了m个(有一条轨迹命中即为该目标命中),则召回率 = m / n
-
预测轨迹准确率:预测了n条轨迹,命中了m条,则准确率 = m / n
# FPR/TPR
- FPR: false positive rate,假正例率,负类数据被分为正类数据的比例
F P R = F P F P + T N FPR= \frac{FP}{FP + TN} FPR=FP+TNFP
- TPR: true positive rate,真正例率,正类数据被分为正类的比例
T P R = T P T P + F N TPR = \frac{TP}{TP + FN} TPR=TP+FNTP
- TPR即为召回率
# AP/MAP
- Mean Average Precision,平均精度/平均精度均值
- 是目标检测算法的主要评估指标
# ROC
- ROC: Receiver Operating Characteristic,受试者工作特性曲线
- ROC曲线以假正例率为横轴,以真正例率为纵轴,在不同阈值下获得坐标点,并连接各个坐标点得到ROC曲线;
- 一般ROC曲线是阶梯状的,当样本足够多时,ROC曲线就变得平滑;
- ROC曲线用来衡量分类器的分类能力,不同算法模型对应不同的ROC曲线,超参数不同的模型也对应不同的ROC曲线;
- 理想的决策阈值是TPR接近于1,FPR接近于0
# AUC
- AUC: Area Under ROC Curve, ROC曲线下的面积
- AUC就是ROC曲线与横轴围成的面积,AUC其实是一个概率,当你随机挑选一个正样本以及负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值,AUC值越大,当前分类算法越有可能将正样本排在负样本前面,从而能够更好地分类,即AUC能够直观评价分类器的好坏;
- AUC衡量的是不管在取什么阈值的情况下模型的性能
【参考文章】
线性回归1
线性回归2
线性回归3
逻辑回归
生成模型和判别模型
生成模型和判别模型
k均值聚类
k均值聚类
变分
变分
重参数化-推荐
重参数化英文解释
checkpoint
checkpoint
checkpoint
数据泄露
数据泄露检测和修复
ELBO证据下界
PR
PR
PR
ROC/AUC
ROC/AUC
created by shuaixio, 2022.07.30