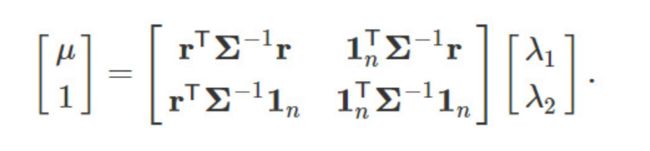马科维茨的均值方差模型(MPT)粒子群优化--Python实现
MPT
MPT, modern portfolio theory。现在资产配置理论。
理论很简单。
假设每个资产的收益率是一个随机变量 x i x_i xi。既然是随机变量，当然就会有均值和标准差。
如果资产数量不是只有一个的话（一个的话，做什么资产配置），也就是存在有多个随机变量，随机变量之间当然就会有协方差。
资产配置的目的就是，找到一种较好的资产配置组合，使得达到预期的收益率的情况下，风险最小。
这句话其实就已经告诉了我们这个模型该如何建立。
建模
E ( r w ) = ∑ i = 1 n w i r i E(r_w) = \sum_{i=1}^{n}{w_ir_i} E(rw)=i=1∑nwiri
V a r ( r w ) = ∑ i = 1 n ∑ j = 1 n w i w j C o v ( r i , r j ) Var(r_w) = \sum_{i=1}^{n}{\sum_{j=1}^{n}{w_iw_jCov(r_i,r_j)}} Var(rw)=i=1∑nj=1∑nwiwjCov(ri,rj)
我们根据上面的加粗文字就可以知道模型应该为：
min w V a r ( r w ) s . t . E ( r w ) = μ ∑ i = 1 n w i = 1 \min_{w}{Var(r_w)}\\ \mathrm{ s.t. } \qquad E(r_w) = \mu \\ \sum_{i=1}^{n}{w_i} = 1 wminVar(rw)s.t.E(rw)=μi=1∑nwi=1
- 上面的模型中的约束如果不加上w应该大于等于0的话，就表示可以卖空，做负的配置。但是做负的配置的时候一般也是有保证金什么的。模型会复杂点。
- 最简单的情况是，考虑到w大于等于0
优化
优化的话，这里使用粒子群优化的方式。
其实一般最常用的是拉格朗日乘子法。
（拉格朗日乘子法是优化的最基础的算法啦，大家直接查就好了。这里我直接截的附件中的图）
- 最后用的是下面这个来解出拉格朗日算子。
- 代入到使得梯度为0的方程解出来的方程中。
粒子群优化
粒子群的思路很简单，就是给一个初始化的向量。然后，每个粒子记住自己的历史最优解和全局的最优解。每次的迭代往这两个方向上加权的偏移就好了。
项目代码
假设有n个产品。cor是它们之间的协方差矩阵。然后，很明显在这个社会中风险越高（方差越大），那么这个产品的收益率越高。
给一个预期的期望收益。由于数据都是随机生成的。这里我们就直接取用在最大和0之间的alpha比例的数值（资产配置不可能高过最高均值收益）
- 给定 α \alpha α,表示在最大和0之间的百分比。alpha取1表示最大值。0表示0。
n = 10
alpha = 0.8
cor = np.random.random((n, n))
mu = np.diag(cor)
EV = alpha * max(mu)
- 添加下面这两个函数，是为了保证生成的分配方式会使得期望收益达到目标设置的值。
def randOne(n):
a = np.random.random(n)
return a / np.sum(a)
def ReCheck(newData, n=10, oriData=None):
for i in range(len(newData)):
if oriData is None:
while np.matmul(newData[i], mu.T) < EV:
newData[i] = randOne(n)
elif np.matmul(newData[i], mu.T) < EV:
newData[i] = oriData[i]
return newData
- m表示有m个粒子来做探索。对其做初始化
- MTime 表示最大迭代周期
m = 30
por = np.random.random((m, n))
por = por / np.sum(por, axis=1)[:, np.newaxis] # 归一
por = ReCheck(por)
w, c1, c2 = 0.6, 2, 2
v = np.random.random((m, n))
MTime = 500
- 计算数值（Objective function）
def CalVal(por):
tmp = 0
for i in range(len(por)):
for j in range(len(por)):
tmp += por[i] * por[j] * cor[i][j]
return tmp
- 粒子群迭代(解释思路)
- 一开始先算出每种分配所对应的总风险
- 然后最初的话，局部最优的结果当然就是初始化的结果。
- 目前已知的全局最优解，一样也就是这些局部最优解的最优解
- 迭代更新速度向量v。这个向量一开始也是随机初始化的。
- 有一个惯性因子w，即表示保持原来的方式飞行。
- c1是局部最优因子;c2是全局最优因子
- 更新好速度向量后。再和原来相加。最后判断对应的数值有没有超过设置的预期均值。
t = 0
while t < MTime:
t += 1
val = np.zeros(m)
for i, p in enumerate(por):
val[i] = CalVal(p)
if t == 1:
local_Min_por = por.copy()
local_Min_val = val.copy()
else:
for i in range(m):
if val[i] < local_Min_val[i]:
local_Min_val[i] = val[i]
local_Min_por[i] = por[i]
global_Min_index = np.argmin(local_Min_val)
global_Min_por = local_Min_por[global_Min_index]
global_Min_val = local_Min_val[global_Min_index]
for i in range(m):
v[i] = w * v[i] + c1 * np.random.rand() * local_Min_por[i] + c2 * np.random.rand() * global_Min_por
new_por = por + v[i]
new_por = new_por / np.sum(new_por, axis=1)[:, np.newaxis]
por = ReCheck(new_por, oriData=por)
效果检验（和蒙特卡洛方法对比）
蒙特卡洛采用完全随机的方式。这里同样的设置总的次数相等。然后再通过不满足对应的期望收益标准的方案就去掉的方式。
random_por = np.random.random((m * MTime, n))
random_por = random_por / np.sum(random_por, axis=1)[:, np.newaxis] # 归一random_
- check and abandon
def ReCheck_abandon(newData):
ansData = newData.copy()
i, j = 0, 0
while i < len(newData):
if np.matmul(newData[i], mu.T) >= EV:
ansData[j] = newData[i]
j += 1
i += 1
return ansData[:j]
random_por = ReCheck_abandon(random_por)
val = np.zeros(m * MTime)[:len(random_por)]
for i, p in enumerate(random_por):
val[i] = CalVal(p)
- 画图
plt.plot(val)
plt.plot([global_Min_val for i in range(len(val))])
- 发现其实存在有不少数结果都比粒子群的方式要好。毕竟粒子群在这里关于粒子移动的速度的设定其实在这种求和受限制的空间的搜索效果并不太好。当然可以适当改进下。（欢迎大家提供改进方案，一起讨论~）
