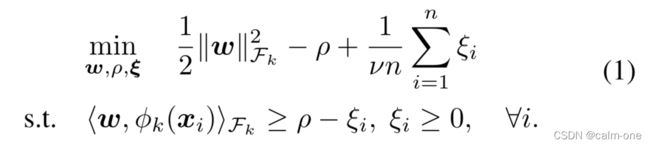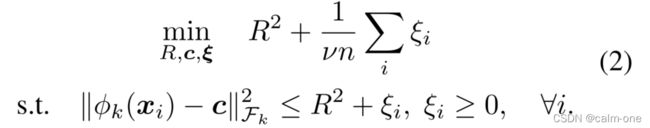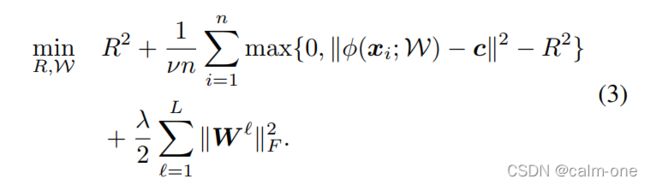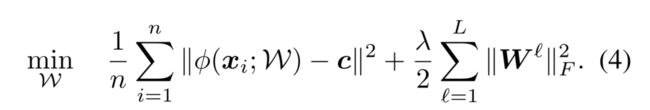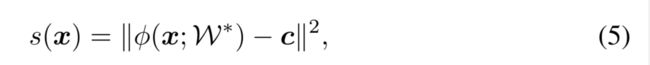【论文精读】一类分类器（一）—DSVDD

论文链接

摘要

尽管深度学习在许多机器学习问题上取得了巨大的进步，但异常检测的深度学习方法相对缺乏。那些存在的方法包括训练网络来执行异常检测以外的任务，即生成模型或压缩，它们反过来适用于异常检测，他们没有训练基于异常检测的目标。在这篇文章中介绍一种新的异常检测方法-DSVDD，训练是基于异常检测目标的。对深层体制的适应需要我们的神经网络和训练过程满足某些性质，这是我们在理论上证明的。我们在MNIST和CIFAR-10(图像基准数据集)上证明了我们的方法的有效性以及检测对抗例子的GTSRB停止标志。

1.介绍

异常检测的任务是识别数据中的异常样本。通常，这被视为一个无监督学习问题，其中异常样本是未知的先验和假设训练数据集的大部分由“正常”数据组成(与高斯分布无关)。我们的目标是学习一个能够准确描述“常态”的模型。偏离这一描述的情况被认为是异常。这也被称为一类分类(Moya等人，1993年)。异常检测算法通常是在机器或系统正常运行状态下收集的数据进行训练进行监控(Lavin & Ahmad, 2015)。其他领域包括网络安全入侵检测、欺诈检测和医学诊断。与许多领域一样，这些领域的数据在规模和维度上都在迅速增长，因此我们需要有效和高效的方法来检测大量高维数据中的异常。

经典的异常检测方法有一类SVM(OC-SVM)或核密度估计(KDE)，经常不能应用于高维、数据丰富的场景由于这类方法具有较差的计算可伸缩性以及维度诅咒。为了有效使用这些浅层方法，通常需要大量的特征工程。相反，深度学习提供了一种自动学习相关特征，成功应用到分类方法中尤其时计算机视觉领域。然而，如何将深度学习的优势转移到异常检测上还不太清楚，因为很难找到正确的无监督的深度目标。目前的深度AD治疗方法已显示出良好的效果，但这些方法都不是通过优化基于AD的目标函数来训练的，通常依赖于基于重构误差的启发式算法。

在本文中，我们提出了一种基于核的一类分类和最小体积估计的深度规划方法。我们的方法，深度支持向量数据描述(Deep SVDD)，它训练神经网络同时最小化包含数据的网络表示的超球体的体积。最小化超球体体积强制网络提取常用的变化因素因为网络必须将数据点紧密地映射到球体的中心。

2. 相关工作

在介绍DSVDD之前，我们简要回顾了基于核的一类分类并介绍了现有的异常检测深度学习方法。

2.1 基于核的一类分类

基于核的一类分类中最突出的方法就是OC-SVM，它的目标就是在特征空间中寻找一个最大的边缘超平面。学习超平面权重使得原始的数据能够在映射空间中被分开。

OC-SVM公式描述，其中第一项是正则项，第二项是超平面距离原点的距离($\rho$)，第三项中 ${\xi }_i$ 是松弛变量允许部分错误数据，$w\text{w}w$ 是学习到的超平面，$\nu \in (0,1]$ 是超参数以平衡学习到的目标，限制条件是超平面 $w\text{w}w$ 和输入数据映射 ${\varphi }_k({x\text{x}x}_i)$ 在希尔伯特空间中的点积大于平面到原点距离(减去一个松弛变量)，$⟨w\text{w}w,{\varphi }_k(x\text{x}x){⟩}_{{\mathcal{F}}_k}<\rho$ 即异常数据。–这里的详细描述见论文

SVDD原始问题描述，这里第一项直接理解为最小化超球体体积即可，第二项同样是使用到松弛变量用于平衡目标，支持向量描述器(SVDD)是与OC-SVM相关的技术，其使用的是超球体划分数据而不是超平面，SVDD的目标是寻找最小的超球体(中心c，半径R)包含大多数的数据。$\Vert {\varphi }_k({x\text{x}x}_i)-c\text{c}c{\Vert }_{{\mathcal{F}}_k}^2>R^2$ 即被认为是异常数据。

OC-SVM和SVDD是非常接近的，两个问题都可以通过他们的对偶问题来解决，即二次规划问题，有很多方法比如序列最小化。在使用高斯核时，这两类问题时等价的以及渐近一致的密度水平集估计问题。形成带有 $\nu$ 的原始问题，$\nu$ 一方面时离群点占比的上界，一方面是支持向量占比的下界。这个结果被称为 $\nu$ 属性，它允许人们将关于训练数据中存在的异常值分数的先验信息纳入模型，即允许训练数据存在异常。

除了实现显式特征工程，上述方法的另一个缺点是由于内核的构造和操作，它们的计算伸缩性较差，除非使用某种近似技术，否则基于内核的方法在样本数量上至少以二次方为单位。此外，使用核方法进行预测需要存储支持向量，这可能需要大量内存。本文中 Deep SVDD 不受这些限制。

2.2 异常检测的深层次方法

深度学习是表示学习的一个子领域，它利用具有多个处理层的模型架构来学习具有多个抽象层次的数据表示。多层次的抽象允许以非常紧凑和分布式的形式表示丰富的特征空间。深层神经网络特别适合于学习本质上是分层的数据表示，例如图像或文本。

我们将试图将深度学习用于异常检测中分为“混合”或“完全深度”。在混合方法中，将这些表示输入经典（浅层）AD方法（如OC-SVM）之前，在前面的步骤中分别学习表示。相比之下，全深度方法直接使用表征学习目标来检测异常。

利用Deep-SVDD，我们引入了一种新的、全深度的无监督AD方法。Deep-SVDD通过训练神经网络，将网络输出拟合到最小体积的超球中，学习提取数据分布变化的共同因素。相比之下，几乎所有现有的深度AD方法都依赖于重建误差—要么是混合方法用于学习表征，要么直接用于表征学习和检测。

深度自动编码器（各种类型）是用于深度AD的主要方法。自动编码器是尝试学习身份函数的神经网络，同时具有降维的中间表示（或一些稀疏正则化）作为瓶颈，诱导网络从一些数据集中提取显著特征。通常，这些网络的训练是为了最小化重建误差。因此，这些网络应该能够从正常样本中提取共同的变异因子，并准确地重建它们，而异常样本不包含这些共同的变异因子，因此无法准确地重建。这允许在混合方法中使用自动编码器，方法是将学习到的嵌入插入到经典AD方法中，但也可以在完全深度的方法中使用，方法是直接将重建误差用作异常分数

用于AD的自动编码器的一些变体包括去噪自动编码器（Vincent et al.，2008；2010）、稀疏自动编码器（Makhzani& Frey，2013）、变分自动编码器（V AEs）（Kingma& Welling，2013）和深卷积自动编码器（DCAEs）（Masci et al.，2011；Makhzani& Frey，2015），最后一种变体主要用于具有图像或视频数据的广告应用（Seeböck等人，2016；Richter& Roy，2017）。

自动编码器的目标是降维，而不是直接针对异常检测。将自动编码器应用于AD的主要困难在于选择正确的压缩程度，即降维。如果没有压缩，自动编码器只需学习标识函数。在另一种情况下，信息减少到一个单一的价值，平均值将是最佳的解决方案。也就是说，数据表示的“紧凑性”是一个模型超参数，由于无监督的性质以及数据的内在维度通常难以估计，因此很难选择正确的平衡（Bengio et al.，2013）。相比之下，我们通过最小化包含超球面的数据量，将表示的紧凑性纳入深度SVDD目标，从而直接将AD作为目标。

除了自动编码器，Schlegl等人（2017年）最近提出了一种基于生成性对抗网络（GANs）的新型深度异常检测方法（Goodfello等人，2014年），称为AnoGAN。在该方法中，首先训练GAN以根据训练数据生成样本。给定一个测试点，AnoGAN试图在生成器的潜在空间中找到生成最接近所考虑测试输入的样本的点。直观地说，如果GAN捕捉到了训练数据的分布，那么正常样本，即分布中的样本，应该在潜在空间中具有良好的代表性，而异常样本则不会。为了找到潜在空间中的点，Schlegl等人（2017）在潜在空间中执行梯度下降，保持生成器的学习权重不变。AnoGAN最终也通过重建误差定义了异常评分。与自动编码器类似，这种生成方法的一个主要困难是如何调整生成器的紧凑性。

3.Deep SVDD

3.1 深度支持向量描述器目标

主要思想：基于核支持向量描述器与最小化体积，寻找包含数据的最小超球体。

理解：通过卷积神经网络学习从输入空间到输出空间的映射，其中输出空间包含所有的一类样本数据，目标就是在输出空间寻找最小的超球体包含所有的一类样本数据，其中包含两个部分一个是网络参数的学习，一个是超球体参数学习，因此论文中提到联合学习(因为无法同时优化这两类参数)。

上式便是DSVDD的优化问题，第一项是超球体体积表示，第二项是样本到超球体中心的距离大于半径程度的衡量（简单理解：若样本在超球体外，使得这一距离最小；若样本在超球体内，直接为0），第三项是正则项防止参数学习过于复杂而造成过拟合。

因为针对一类分类，因此简化问题，不再优化半径 $R$，仅仅训练权重使得样本距离中心最近，个人理解就是将网络优化问题不再看成超球体优化问题，即学习一种表示使得最后的样本映射足够紧凑，公式简化成下式。

从公式中可以发现不再优化 $R$，同时没有 $\nu$ 指的是优化目标不在惩罚不在超球体外的异常点而是优化所有数据到原点的距离的平均。第二项同样是正则化参数项。

异常分数定义，即数据经过带有参数的函数映射后距离原点的距离。对于软边界DSVDD，将这一分数减去训练好的 $R^{\ast }$，网络的参数 ${\mathcal{W}}^{\ast }$ 和 $R^{\ast }$ 完全描述了网络，在预测阶段没有数据存储。这个应该是和传统方法比较得到的-个人感觉其实这些就是需要存储的数据。

3.2 优化DSVDD

通过随机梯度下降(SGD)及其变体Adam，在两个目标函数中使用反向传播算法对参数进行优化，使用SGD可以让DSVDD很好地扩展到大型数据集上，因为其计算复杂度与训练批次的数量呈线性关系，每个批次都可以并行处理。因为网络参数 $\mathcal{W}$ 和 $R$ 具有不同的尺度，而使用同样的SGD算法去优化是比较低效的，因此本文提出采用交替最小化/块坐标下降法交替优化网络参数和半径，即训练k轮得到网络参数 $\mathcal{W}$ 时固定 $R$ ，在第k轮时使用最新的参数 $\mathcal{W}$ 计算半径。$R$ 可以通过简单的线性搜索得到解决。

3.3 DSVDD的性质

上文公式中对于超球体的中心并没有详细描述，而对于不合适的网络结构以及超球体中心，DSVDD学习到的时一些琐碎的、不含信息的解决方案。
【命题1】（全零权重解决方案）.
将初始训练权重全部设置成0，将映射输出 ${c\text{c}c}_o$ 作为超球体中心。证明了不可取
替代方案是初始化网络输出输出均值作为中心点 $c\text{c}c$
【命题2】（偏执项）
训练权重不应该带有偏执项，否则会导致权重为0时，任意输出为偏执导致的唯一输出作为最优解，显示这是不合适的，因此需要避免带有偏执进行训练
【命题3】（有界激活函数）
如果使用有界激活函数，那么对于同一样本的输出会趋于饱和，到深层网络的时候就相当于学习了偏执项，因此最优解会趋向于一个值造成超球体崩塌现象。因此需要选择无界激活函数。

上面三个命题都是围绕超球体中心展开，都需要避免，否则网络学习会区域权重全是0的情况

【命题4】（ $\nu$ 属性）
$\nu$ 控制着离群值分数的上界和样本分数在超球边界外或边界上的下界

4. 实验

这部分首先比较特别的是：训练阶段没有使用标签，测试阶段使用了标签。

4.1 完成方法

浅层基准 （1）带有高斯核的OC-SVM/SVDD；（2）核密度估计（KDE）；（3）孤立森林
深度基准和DSVDD （1）和DCAE编码器进行对比；（2）和AnoGAN进行对比；（3）DSVDD

DSVDD的实验设置，将所有网络的偏执项去除，每5轮进行线性搜索得到 $R$ ，选择 $v\in \{0.01,0.1\}$，设置超球体的中心为初始网络前向传递映射结果的均值，使用带参数的Adam优化器，并且使用批归一化，与之对比的深度异常检测网络初始化使用 uniform Glorot 权值，而DSVDD使用训练好的DCAE权重作为初始化，从而形成预训练效果。两阶段学习率(搜索+微调)来确定初始学习率，激活函数使用 Leaky Relu

4.2 MNIST和CIFAR-10上的一类分类

设置 两个数据集都建立10类的一类分类，每个配置中，其中一类是正常数据，其他类都是异常数据。实验中，使用原始的训练和测试划分，并且只使用来自各自的正常类的训练集示例进行训练。这为MNIST提供了n=6000的训练集大小，为CIFAR-10提供了n=5000的训练集大小，两个测试集都有10000个样本，包括来自每个设置的9个异常类的样本。我们使用L1-范数对所有图像进行全局对比度归一化预处理，最后最小最大放缩到 [0, 1]
网络结构 在MNIST上，我们使用了一个有两个模块的CNN, 8×(5×5×1)filters和4×(5×5×1)filters，以及最后一个32个单元的密集层。在CIFAR-10上，我们使用一个有三个模块的CNN, 32 × (5 × 5 × 3)filters，64×(5×5×3)filters和128×(5×5×3)filters，最后是128个单元的密集层。我们使用批次大小为200，设置权值衰减超参数 $\lambda =10^{-6}$ .
结果

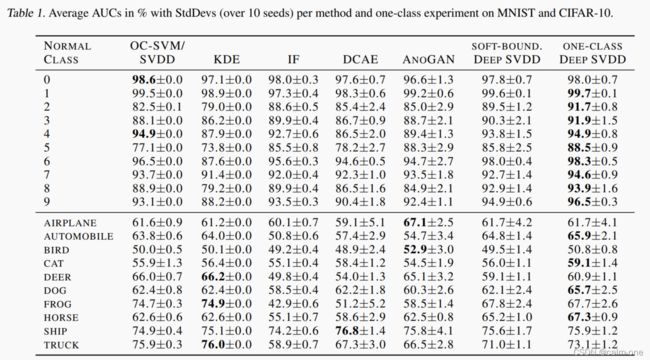
在MNIST数据集上DSVDD方法效果较好，而CIFAR-10中的SVDD和KDE的方法比DSVDD效果好，作者认为KDE具有良好的全局结构所以使用CNN的方法便存在问题，这便是网络结构选择的问题。而硬边界DSVDD方法比软边界方法好，作者认为这训练集不存在异常数据假设一致，同时随着SGD优化，网络具有较高的标准差。

4.3 在GTSRB停止标志上的对抗攻击

训练集包含n = 780个停止标志，测试集由270个正常样本和20个对抗样本组成，这部分详细说明见论文，结果如下：

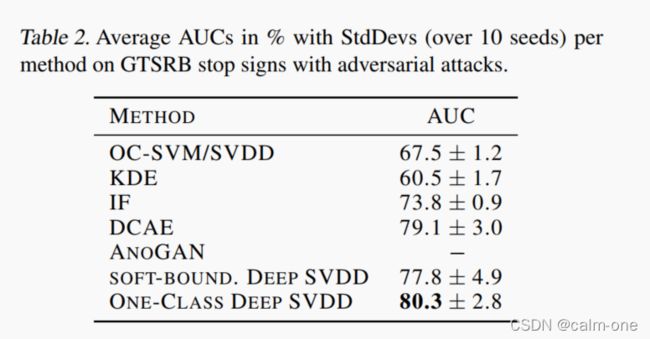
5. 总结

引入了第一个深度的无监督AD单类分类目标DSVDD，联合训练一个深度神经网络，同时在输出空间中优化一个包含数据的超球体。通过这种Deep SVDD从数据中提取出共同的变异因子。我们已经演示了我们的方法的理论性质，比如 $\nu$ 属性，它允许在数据中包含对异常值数量的预先假设。我们的实验定量和定性地证明了Deep SVDD的性能。