推荐系统的因果推断：Causal Inference for Recommender Systems（RecSys，2020）

说明

这篇博客是一篇论文的学习笔记。

---

1. 推荐和因果

推荐系统（Recommender System），大家都很熟悉了。
推荐系统的任务为预测 “用户偏好”和“用户评分”。

因果推断（Causal Inference）是确定作为更大系统组成部分的特定现象的独立实际影响的过程。

那么，推荐是如何和因果推断产生关系的呢？
作者认为：
推荐是因果推断！
因为：在预测时，推荐系统尝试回答

“如果一个用户看了一部电影，那么她会怎么评价呢？”

如果我们让用户接触（不接触）电影，评分会是多少？这就是一个关于干预的问题。那么就引出了因果推断问题中的干预（Intervention） 问题。这种因果推断中的关键挑战是未观察到的混杂因素（unobserved confounders），这些变量会影响用户决定与哪些项目进行交互以及他们如何评价它们。

举个例子：
由于用户观看了特定导演的许多电影，因此他们可能经常被推荐该导演的电影并且也倾向于观看和喜欢这些电影。导演是一个使推论产生偏差的混杂因素；它会影响用户被推荐的电影以及他们是否观看和喜欢它们。

简单理解，如果不处理混杂因素，那么得出的推荐是有偏差的，也即是不可信的。

---

2. 理论做法

2.1. 符号说明

首先给出下面描述需要用到的符号以及它们的意义：

符号	意义
$u$	某一个用户
$i$	某一部电影
$a_{ui}$	$u$ 是否对 $i$ 评分的标志
$y_{ui}(1)$	如果 $u$ 看过 $i$，$u$ 对 $i$ 的评分。这个评分仅当 $u$ 看过并且评价过 $i$ 时是可观察到的；否则就是未观察到的。
$y_{ui}(0)$	如果 $u$ 没有看过 $i$，$u$ 对 $i$ 的评分。通常，$y_{ui}(0)=0$
$\left(y_{ui}(0),y_{ui}(1)\right)$	潜在结果
$\{a_{ui},u=1,\dots ,U,i=1,\dots ,I\}$	包含（二元）曝光的数据集。它指示了谁看了什么
$\{y_{ui}(a_{ui})\mid (u,i),a_{ui}=1\}$	用户看过的电影评分数据集

2.2. 潜在结果下的矩阵分解

在推荐系统的矩阵分解中，将原始评分矩阵 $R$ 分解为用户偏好矩阵 $X$ 和项目属性矩阵 $Y$，即：
$$R_{U\times I}\approx X_{U\times K}{Y}_{K\times I}.$$
其中，$K$ 为指定的维度，$K\ll U,I$。

在潜在结果下，重组矩阵分解。输出模型如下：
$$y_{ui}(a)={\theta }_u^{\mathrm{T}}{\beta }_i\cdot a+{ϵ}_{ui},{ϵ}_{ui}\sim \mathcal{N}(0,{\sigma }^2)\text{(1)}$$
其中，${\theta }_u$ 是用户偏好，${\beta }_i$ 是项目属性。

• 当 $a=1$ 时（$u$ 看过 $i$），该模型表示评分来自高斯分布，其均值结合了 ${\theta }_u$ 和 ${\beta }_i$。
  $$\begin{array}{rl}\mathbb{E}\left[y_{ui}(a)\right]& =\mathbb{E}\left[y_{ui}(1)\right]\\ & =\mathbb{E}\left[{\theta }_u^{\mathrm{T}}{\beta }_i+{ϵ}_{ui}\right]\\ & =\mathbb{E}\left[{\theta }_u^{\mathrm{T}}{\beta }_i\right]+\mathbb{E}\left[{ϵ}_{ui}\right]\\ & ={\theta }_u^{\mathrm{T}}{\beta }_i\end{array}.$$
• 当 $a=0$ 时，评分是零均值高斯。
  $$\mathbb{E}\left[y_{ui}(a)\right]=\mathbb{E}\left[y_{ui}(0)\right]=\mathbb{E}\left[{ϵ}_{ui}\right]=0.$$

拟合方程 (1) 对观察到的数据恢复了经典的概率矩阵分解。它的对数似然只涉及观察到的评分；它忽略未曝光的项目。

2.3. 忽略性假设

方程 (1) 并没有给出 $y_{ui}(1)$ 的无偏因果推断。潜在结果理论告诉我们，只有在忽略性（ignorability）假设下估计 $y_{ui}(1)$。对于所有的用户 $u$，忽略性要求 $\{{\mathbf{y}}_{\mathbf{u}}(0),{\mathbf{y}}_{\mathbf{u}}(1)\}\perp \perp {\mathbf{a}}_u$，其中 ${\mathbf{y}}_{\mathbf{u}}(a)=\left(y_{u1}(a),\dots ,y_{uI}(a)\right)$，${\mathbf{a}}_u=\left(a_{u1},\dots ,a_{uI}\right)$。也就是说，用户观看的电影向量 ${\mathbf{a}}_u$ 和如果她看完了所有电影并且如何评分 ${\mathbf{y}}_u(1)$ （如果都没看的话，就是 ${\mathbf{y}}_u(0)$）之间相互独立。

很显然，忽略性假设并不满足。

2.4. 经典因果推断

将推荐框架化为因果问题与传统方法不同。传统方法从观察到的评分数据构建模型，通常是矩阵分解，然后使用该模型来预测看不见的评分。
如果用户随机观看电影，在上述干预意义上，这种策略才能提供有效的因果推断。（类似于临床随机试验，不现实的试验条件。）

用户（通常）不会随机看电影，因此从观察的评分数据中回答因果问题具有挑战性。问题是可能存在影响处理分配（用户观看哪些电影）和结果（他们如何评价它们）的混杂因素（confounders）。

当可忽略性不成立时，经典因果推断要求我们测量和控制混杂因素。这些是影响曝光和评分的变量。以用户的位置为例，它会影响他们看的电影以及（也许）他们喜欢什么样的电影。

假设我们测量了每个用户的混杂因素 $w_u$，满足 $\left\{{\mathbf{y}}_u(0),{\mathbf{y}}_u(1)\right\}\perp \perp {\mathbf{a}}_u|w_u$。
结果模型为：
$$y_{ui}(a)={\theta }_u^{\mathrm{T}}{\beta }_i\cdot a+{\eta }^{\mathrm{T}}{w}_u+{ϵ}_{ui},{ϵ}_{ui}\sim \mathcal{N}(0,{\sigma }^2).$$
但是上述模型要求测量所有的混杂因素，这种假设也被称为强忽略性（strong ignorability）。然而，这是不现实的。

3. 去混杂因素推荐器

作者提出了一种为未观察到的混杂纠正经典矩阵分解的去混杂推荐器（deconfounded recommender）。
去混淆推荐器建立在推荐数据中的两个信息源之上：每个用户决定观看哪些电影以及用户对这些电影的评分。
它假设这两种类型的信息来自不同的模型——曝光数据来自用户发现要观看的电影的模型； 评分数据来自用户决定他们喜欢哪些电影的模型。
评分数据涉及两种类型的信息——用户只对他们看过的电影进行评分——因此经典矩阵分解受到曝光模型的影响，即用户不是随机接触电影的。

去混淆推荐器试图纠正这种偏见。去混淆推荐器包含两个模型。第一个模型使用曝光数据来评估一个用户可能考虑的电影模型。接着使用这个曝光模型来估计一个不可观察混杂因素的替代品。其次，它使评价模型适合考虑替代混淆因素。

关键思想是推荐系统的因果推理是一个多重因果推理问题：有多种处理方法。每个用户对每部电影 $a_{ui}$ 的二元曝光是一种处理；因此，每个用户都有 $I$ 种治疗方法。评分向量 ${\mathbf{y}}_u(1)$ 是输出；这是一个 $I$ 维向量，其中的部分是可观察的。处理的多样性使带未观察到的混杂因素的因果推断成为可能。

3.1. 曝光模型

第一步是将模型拟合到曝光数据。我们使用泊松分解 (Poisson Factorization，PF) 模型。PF 假定数据来自于：
$$a_{ui}\mid {\pi }_u,{\lambda }_i\sim \text{Poisson}({\pi }_u^{\mathrm{T}}{\lambda }_i),\forall u,i\text{(2)}$$
其中，${\pi }_u{\sim }^{iid}\text{Gamma}(c_1,c_2)$，${\lambda }_i{\sim }^{iid}\text{Gamma}(c_3,c_4)$。
用户向量 ${\pi }_u$ 捕获了用户偏好，而项目向量 ${\lambda }_i$ 捕获了项目属性。

使用拟合的 PF 模型，去混杂的推荐器计算未观察到的混杂因素的替代品。它从 PF 拟合重建曝光矩阵 $\hat{a}$：
$${\hat{a}}_{ui}={\mathbb{E}}_{\text{PF}}\left[{\pi }_u^{\mathrm{T}}{\lambda }_i\mid \mathbf{a}\right],\text{(3)}$$
其中 $\mathbf{a}$ 是观察到的所有用户的曝光，并且期望取自 PF 模型计算的后验。
这是 ${\pi }_u^{\mathrm{T}}{\lambda }_i$ 的后验预测平均值，用作替代混杂因素。

最后，去混杂的推荐器建立了一个以替代混杂因素 $\hat{a}$ 为条件的结果模型，
$$y_{ui}(a)={\theta }_u^{\mathrm{T}}{\beta }_i\cdot a+{\gamma }_u\cdot {\hat{a}}_{ui}+{ϵ}_{ui},{ϵ}_{ui}\sim \mathcal{N}(0,{\sigma }^2)\text{(4)}$$
其中 ${\gamma }_u$ 是一个用户特定的系数，描述了替代混杂因素 $\hat{a}$ 对评分的贡献程度。
去混淆推荐器将此结果模型与观察到的数据相匹配；它通过最大化后验估计（maximum a posteriori，MAP） 估计推断出 ${\theta }_u$、${\beta }_i$、${\gamma }_u$。方程中 (4) 的系数 ${\theta }_u$，${\beta }_i$ 只适合观察到的用户评分（即 $a_{ui}=1$），因为 $a_{ui}=0$ 会将涉及他们的项置零；相反，系数 ${\gamma }_u$ 适合所有电影（$a_{ui}=0$ 和 $a_{ui}=1$），因为 ${\hat{a}}_{ui}$ 总是非零。

为了形成推荐，去混淆推荐器使用拟合的 ${\theta }_u$，${\beta }_i$，${\gamma }_u$ 计算所有潜在评分 $y_{ui}(1)$。然后它对未看过的电影的潜在评分进行排序。这些是因果推荐。

3.2. 结果模型

推荐器包含两个模型，一个用于曝光，一个用于输出。
PF 作为暴光模型和概率矩阵分解作为结果模型。
矩阵分解的一般形式：
$$y_{ui}(a)\sim p\left(\cdot |m({\theta }_u^{\mathrm{T}}{\beta }_i,a),v({\theta }_u^{\mathrm{T}}{\beta }_i,a)\right)\text{(5)}$$
其中，$m({\theta }_u^{\mathrm{T}}{\beta }_i,a)$ 和 $v({\theta }_u^{\mathrm{T}}{\beta }_i,a)$ 分别表征评分 $y_{ui}(a)$ 的均值和方差。

这种形式包含许多分解模型，包括概率、加权和泊松矩阵分解。
然后，去混淆的推荐器拟合一个增强的结果模型 $M_Y$ 。这个结果模型 $M_Y$ 包括替代混杂因素：
$$y_{ui}(a)\sim p\left(\cdot |m({\theta }_u^{\mathrm{T}}{\beta }_i,a)+{\gamma }_u{\hat{a}}_{ui}+{\beta }_0,v({\theta }_u^{\mathrm{T}}{\beta }_i,a)\right)\text{(6)}$$
其中，参数 ${\gamma }_u$ 是用户特定的系数；对于每个用户，它表征替代混杂因素 $\hat{a}$ 对评分的贡献程度。
这些去混淆的结果模型可以通过 MAP 估计来拟合。

3.3. 为何有效？

PF 从曝光矩阵 $a_{ui}$ 中学习一个每个用户的潜变量 ${\pi }_u$，作为替代混杂因素。
证明这种方法的理由是 PF 承认一个特殊的条件独立结构：以 ${\pi }_u$ 为条件，处理 $a_{ui}$ 是独立的（等式 (2)）。如果曝光模型 PF 很好地拟合了数据，那么每个用户的潜在变量 ${\pi }_u$（或它的函数，如 ${\hat{a}}_{ui}$）捕获了多重处理混杂因素，即与多次曝光和评分向量相关的变量。我们注意到真正的混杂机制不需要与 PF 一致，真正的混杂机制也不需要与 ${\pi }_u$ 一致。相反，PF 会产生一个替代混杂因素，足以消除混杂因素。

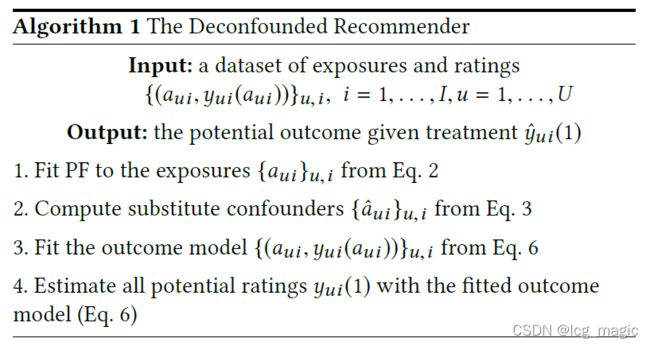
3.4. 算法

---

4. 实验

4.1. 评价指标

Recall：召回率

NDCG：
$${\text{err}}_{\text{rand}}=\frac{1}{U}\sum _{u=1}^{U}l\left({\left\{{\hat{y}}_{ui}\right\}}_{i\in {\mathcal{I}}_u},{\left\{y_{ui}(1)\right\}}_{i\in {\mathcal{I}}_u}\right)$$
其中 $l$ 是损失函数，例如均方误差 (mean squared error，MSE) 或归一化贴现累积增益 (normalized discounted cumulative gain，NDCG)；从所有项目中随机选择的子集 ${\mathcal{I}}_u$。

---

【参考】

1. YixinWang, Dawen Liang, Laurent Charlin, and David M. Blei. Causal inference for recommender systems. Proceedings of the fourteenth ACM conference on recommender systems (RecSys ’20). 2020: 426–431.
2. Wikipedia: Recommender System.
3. Wikipedia: Causal Inference.

【修改记录】

时间	内容
2022年4月20日16:30:05	参考文献格式