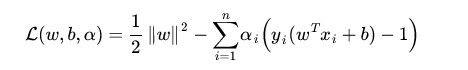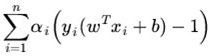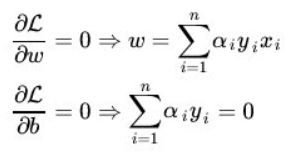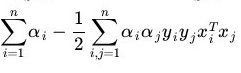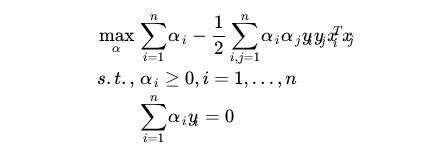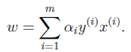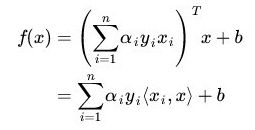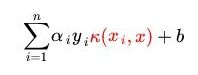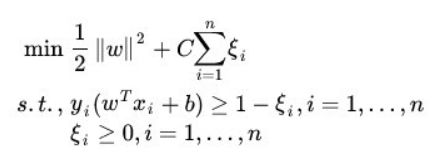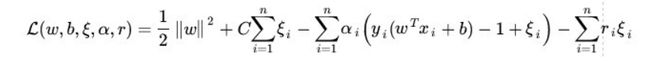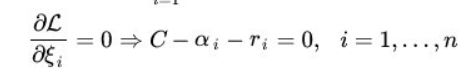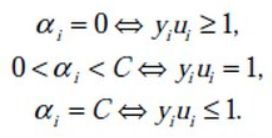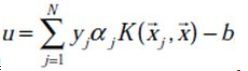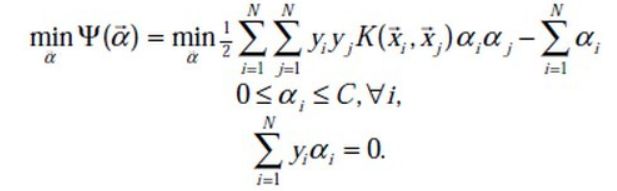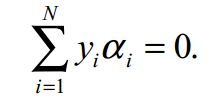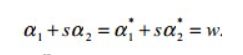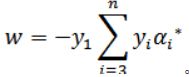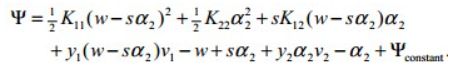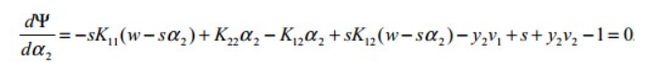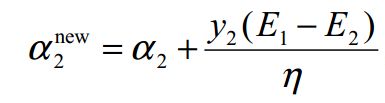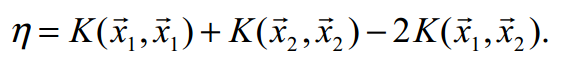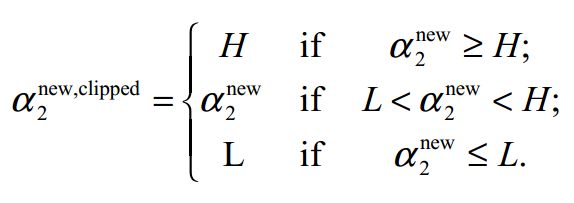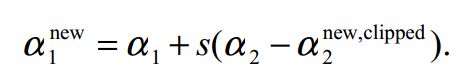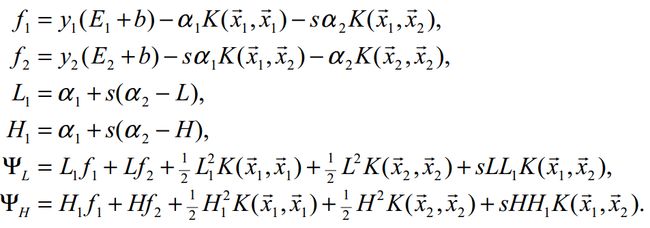支持向量机(SVM)
断断续续看了好多天,赶紧补上坑。
感谢july的 http://blog.csdn.net/v_july_v/article/details/7624837/
以及CSDN上淘的比较正规的SMO C++ 模板代码。~LINK~
1995年提出的支持向量机(SVM)模型,是浅层学习中较新代表,当然Adaboost更新一点。
按照Andrew NG的说法: "SVM的效果大概相当于调整最好的神经网络。"于是,SVM被各种神化,被誉为"未来人类的希望,世界人民的终极武器"。
甚至是IEEE选举的数据挖掘十大算法中唯一一个神经网络,对,没错,SVM就是个MLP。
SVM忽悠大法第一条“我有核函数!":
傻子都知道RBF径向基核函数在SVM发明的7年前就已经被用于RBF神经网络,RBF网络本质就是个把激活函数从Sigmoid替换成RBF的MLP。
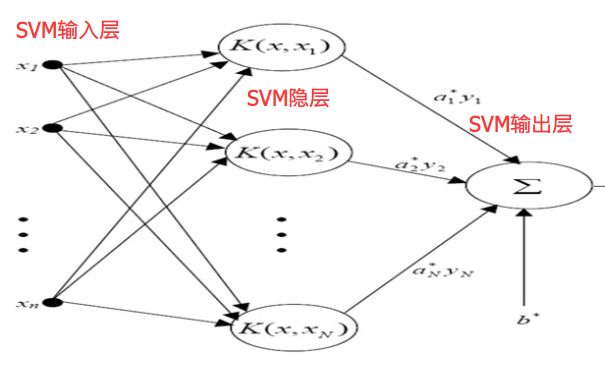
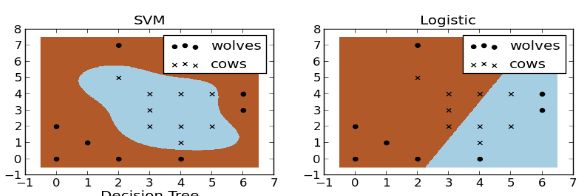
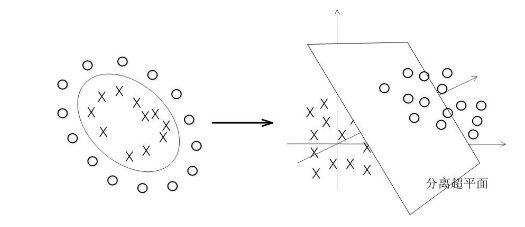
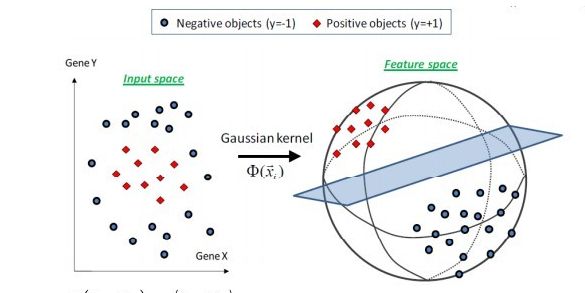
SVM处理线性不可分的能力大致来自于两个部分,非线性映射(重点)、高维空间(核函数)。
SVM的非线性映射藏的比较隐秘,来自其伪·隐层结构:支持向量神经元层。至于核函数?就是个激活函数罢了。
实际上Logistic-Sigmoid函数也是核函数之一,Logistic回归不能处理线性不可分问题,并不是因为没有核函数,其实它有。
缺乏非线性映射变换的隐层结构,才是只能画线,不能画圆的关键,在这点上,不从神经网络角度理解SVM,是很容易产生误解的。
RBF较之于Sigmoid,确实有更快的收敛、更精确的逼近,但是,径向范围σσ的选取并非易事,过大过小都会影响映射,至于SVM中默认
取定值的做法?其实并不完美。
SVM忽悠大法第二条“我分类效果好":
SVM的最优间隔理论,从数学上来讲,very good,其效果也比直接用Gradient Descent拟合好。
当然,这得益于SVM的分类环境假设:一刀切二类分类。但是,更多情况下是K类分类。
SVM确实有多类改进方法,比如基于投票机制的KNN-SVM,但是效果并不好。
相比于传统神经网络天然的多分类输出层,比如Softmax,逊色不少。
尤其在深度学习里,当样本和训练时间不作为第一要素、精度由深度网络保证,SVM的作用就弱化不少。
比如用户物体识别的ImageNet网络里,共有1000类需要分类,训练多个SVM,来达到多分类的目的,效果不会很好。
原因正如Bengio吐槽决策树那样,样本的输入空间被切分后,全样本之间的稀疏特征被分离,不利于整体的协同表达。
当然这在浅层学习中,尤其是在数据挖掘这类的统计数据上,问题并不是很大。
SVM的优势:
SVM本质就是个MLP,但是这个MLP真的很赞,它智能地解决了MLP中隐层神经元个数问题。
自MLP结构发明以来,隐层数、隐层神经元个数一直是最头疼的地方。
比如,世界上的许多骗钱模拟大脑计划,大喊着要模拟人脑840亿个神经元,疯狂在隐层上做文章。纯粹在浪费时间。
SVM直接出来打脸:隐层神经元无须很多,只要覆盖支持向量即可。
其次,径向基函数的径向基中心选取,在二次规划的求解当中也被解决,而无须依靠训练。
SVM的劣势:
来自深度学习大师Yoshua Bengio的吐槽:
学习好的表示(representations)是深度学习的核心目的,而非像 SVM 一样就是在特征的固定集合做一个线性预测。(吐槽 SVM 用 kernel 转移重点)。
SVM终究是MLP,精确的MLP,但并不是拯救世界的神器,它只不过是浅层学习这个”数值游戏“的大赢家。
尺有所短,寸有所长。对于SVM和传统神经网络,我们的态度应该是不吹不黑。知其然,知其所以然。
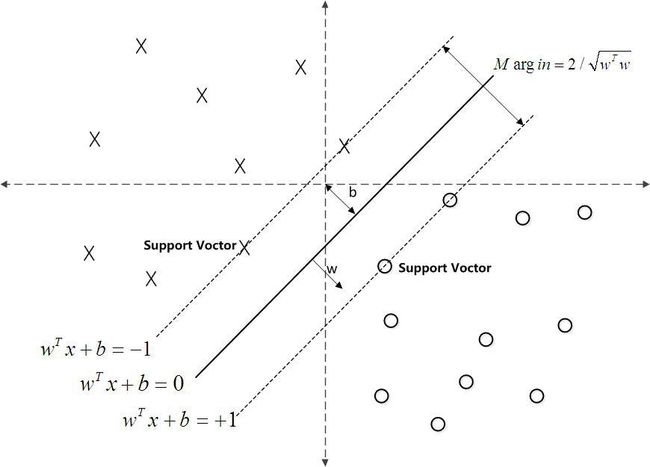
①最大化几何间隔。
如果数据能一道线切开的话,我们希望离这道线最近的点的距离越长越好,否则容易分类错误,这就是SVM的核心。
定义函数间隔di=y(wxi+b),其中y=1 or -1,问题在于2*di和di是等效的分隔平面,所以弃之。
所以又定义几何距离D=d/||w||。||w||=根号(w1^2+w2^2+...wn^2)
目标函数max D,约束条件di=y(wxi+b)>=d, 这里的d是取最小的函数间隔,保证离分割平面最近,且最大化距离。
化简处理:令w’=w/d, b’=b/d, 这样约束条件等式相当于两边被除了d,变成di=y(w’xi+b)>=1,
D也相当于变成1/||w||,为了方便,以后w’全部用w代替。
di=y(wxi+b)>=1, 这是个有趣的式子,由于y=±1,单独取出(wxi+b),那么±1的就是传说中里分隔平面最近的点了,称之为支持向量。
②探究规划问题
目标函数=max D=max 1/||w||,分式好讨厌,等效成min![]() (数学原理不知道是啥=。=)
(数学原理不知道是啥=。=)
然后引入拉格朗日乘子α,把目标函数、约束条件捆在一起成一个式子。
min针对的是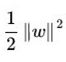 ,注意看min/max底部,不要很矛盾地理解成对整个式子。
,注意看min/max底部,不要很矛盾地理解成对整个式子。
max部分是重点,引入变量α,成为拉格朗日乘子。max这部分的意义在于等效约束条件,
由于y(wxi+b)>=1,如果出现小于1的情况,那么减去的这部分就是一个负数,负负得正,会使前面的min黯然失色。至于大于1的情况,可以令α=0 踢掉它。
然而这个式子还是比较麻烦的,min规划是先决条件,然后还要考虑不定的乘子部分。
利用拉格朗日对偶性大法,逆转下两个条件,变成对偶规划问题。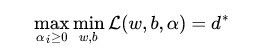 ,要满足KKT条件,就有d*<=p*。
,要满足KKT条件,就有d*<=p*。
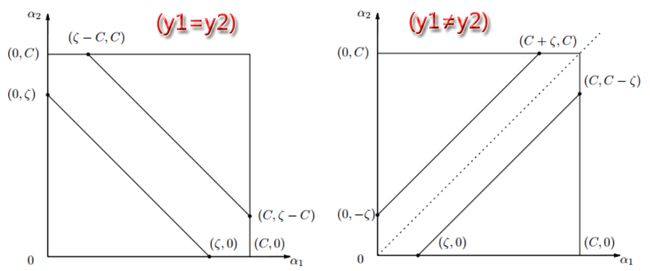
KKT条件说白了就是0<α 这样就可以先定住max求min,最后再求max了。 ③大道至简 上面这个目标函数的min(主元是w、b) 部分化简很神奇,先分别对主元w和b求偏导,令偏导数为0。 第一个偏导结果巧妙地用alpha、y、x替代了恶心的w 第二个偏导结果则是带来了一个新的约束条件,好处是化简目标函数时消掉了b,坏处是给计算alpha乘子带来麻烦。(由此SMO算法诞生了) 将w的代替式拖到 加上max和两个约束条件之后 max部分将由SMO算法完成,SMO每次抽取确定两个乘子,然后更新w、b 更新w:。 更新b: 这个b比较好玩,w确定之后,实际上分隔平面的方向被确定了。 想想一次函数y=wx+b,如果b没确定,则这个一次函数就可能是两个边界间任意一条直线。 那么b应该是什么值呢,应该取两条边界的中间那条比较好。(SMO中b也不能这么干) ④分类函数 训练数据时,需要一个预测分类函数,以便算出误差E。(这个E在SMO中至关重要) 分类函数自然就是带入式子y=wx+b,但是这可不是二元一次方程,w是多维的。 ⑤SVM的超级武器——核函数 特征空间的映射的引入使得SVM秒掉了各种回归模型。它的原理就是将低维度数据,映射到高维度数据。 比如原来数据是2维,如果是非线性数据,很难划分隔面。但是给它加到5维,就很容易一刀切出划分面了。 巧妙的映射了维度,这对分类函数中的内积计算产生了影响,为了计算在高维空间的内积,出现了核函数。 目前使用的核函数通常是 "高斯核“函数,又名径向基核函数。 ⑥松弛变量的优化 outlier(异常值)是SVM需要解决的一个问题。 如果就存在一个异常值,离分隔平面超级超级超级近,设这么一个垃圾值为支持向量显然不是明智选择。(间隔越小,平面越难被划分,分类效果就越差) 所以引入松弛变量,使得原目标函数变为 切入约束条件后,拉格朗日函数变成: 然后按照⑤中方法化简,多了一个新主元,并求导令倒数为0。 你不必关系ri是什么,只要知道ri>=0即可,移个项,αi=C+ri。实际意义就是αi多了一个上界C。 同⑤中那样化简拉格朗日函数,最后惊奇发现,松弛变量被消了,和⑤最后的式子一样。 其实松弛变量引入的唯一变化,就是多了个KKT条件多了个上界C。(C的取值很难说,模板代码里取的是100) )新的KKT条件如下: α=0,表示非支持向量点。 0<α α=C,表示的是两条支持向量间的outlier(这些点通常被无视掉) ⑥SMO算法 1998年4月,位于总部的微软研究院副主任John Platt发明了这个奇怪的SMO算法,从此SVM超神了。 John Platt那篇论文省去了公式推导,所以大部分情况都是,直接给你个XX情况的公式是XX,以及给出的很残破的C伪代码 对初学者很不友好,链接 ~Link~,想要完全解释清楚还是比较难的。 感谢CSDN某网友提供的完整的SMO的C++代码,里面的变量名几乎与John Platt论文中的C伪代码一致。 Part I SMO的公式推导 ①新的分类函数与新的目标函数 SMO定义了新的分类函数u,其实也不算新,就是把b的符号变了。 这个式子就是把y=wx-b,w替换了而已,上面已经出现了类似物了。 也定义的新的目标函数 减号两边换一下,从max变成了min,意义不明。 ②两个乘子问题 还记得这玩意不,偏导出来的坑爹约束条件。 假设我们每次抽取一个乘子,设为α1,那么改了α1之后,能保证上面那个约束条件成立么?很可惜,不好办。 所以John Platt提出了SMO(最小序列算法),他认为至少(最小)要同时改变两个乘子。 分为主动乘子(α2)和被动乘子(α1)。每次主动算α2,然后根据约束条件,推出α1的值,这样α1光荣地做了嫁衣。 一个有趣的想法,比如这次搞定了α2,到了下一次,上次的α2又变成了α1,被动算出来之后,会不会导致上次的α2过程白算了?然后恶性循环? 其实想多了,实际测试,每次抽两个乘子,只会使结果变好,而不会卡死在循环里。 于是算α2成为头等大事。 先确定α2的范围,已有约束条件:0<=α1<=C, 0<=α2<=C (称为矩形条件) y1α1+y2α2=γ,γ=Σ(yi*αi),i=3,4....,m(那个头疼的约束条件,提取出两项) 由于yi=±1, 这里分两种情况。(γ不知道正负) 情况1: y1=y2 y1α1+y2α2=γ => α1+α2=±γ(两条直线) 情况2:y1≠y2,即异号。 y1α1+y2α2=γ => α1-α2=±γ(两条直线) 画个图 这样当y1=y2,α2有下界L=max(0,γ-C),上界H=min(γ,C) y1≠y2,α2有下界L=max(0,-γ),上界H=min(C-γ,C) 注意这里的α2称之为α2(new),原来的α2称为α2(old),同时下面所有打(*)号的变量都是old变量。 α2的具体值怎么确定呢?有如下推导。 首先,抽取两个乘子后,目标函数被剖分成这样 就是把i、j∈[1,2]的部分提出来了,但是至今不理解vi部分是怎么出来的。 对α2求导并令导数为0: 化简: 化简: 令ui-yi=Ei,继续化简,有: 裁剪α2(new): 算出α1(new) 特别的,当η<0时,违反了Mercer条件,目标函数为可能∞,这时候α2不能使用上述方式计算,论文中这么写 看不懂,填坑,先按模板代码来。 ③启发式抽取乘子。 尽管α1是被动乘子,我们还是得先抽取α1,然后启发式抽取α2。 启发式(经验式)主要是根据已有经验来安排三种抽取乘子的顺序。 最坏情况其实就是O(m)扫一遍全部数据找到一个α2,当然启发式原则保证我们的RP不会那么差。 一、非边界(0 or C)最大化|E1-E2|规则:选择绝对值最大的先计算。 二、非边界随机规则:非边界alpha里随机选择α2 三、含边界随机规则:实在没有办法了,算上边界再随机吧。 ④收敛条件 由于每次计算α2时,都是由导数决定的,也就是说,每次新的α2产生,都标志着目标函数的优化。 一旦全部α2收敛(即全部乘子收敛,α1若不收敛,下次可能作为α2被调整),则标志着目标函数优化完毕。 SMO主循环遍历全部数据点选择α1(mainProcess函数) 次循环随机/最大化|E1-E2|规则选择起点开始遍历选择α2 (exampleExamine函数) 相当于两层for循环验证全部乘子对,保证最后的目标函数是收敛的。 ⑤双乘子下的几个参数求法 一、α1 α1先通过公式 若违反KKT条件,则设为边界,并按照约束条件对α2进行增/减。 二、b John Platt不知道从哪搞来的公式。目前不知道推导过程。 双乘子情况下求b,论文中这么解释: ③α1、α2均在边界,则取b1、b2均值 ④α1、α2均非边界,则b1=b2,所以①、②任取一个就行了。 三、w Part Ⅱ SMO的C++代码研究 (坑ing) 一、SMO主过程。 这个过程由两个Bool值控制,numChanged 、 examineAll. 首先第一遍检查全部乘子,之后检查非边界乘子(边界乘子的值通常不会改变了),查不到了再重新检查全部,如果全部还查不到,则结束,计算完毕。 检查并修改乘子是一个智能的过程,综合使用三种手段。 alpha1直接获取,由于每个乘子对应一条训练数据,所以该条数据误差E1=预测值-真实值,预测值就是把该条数据带入学习方程(分类函数里)去 分类: 机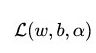 里,经过复杂的化简(详见July大神博客),b也被新的约束条件(为0)给消去了。
里,经过复杂的化简(详见July大神博客),b也被新的约束条件(为0)给消去了。![]() ,即 a1 = alph1 - s * (a2 - alph2)
,即 a1 = alph1 - s * (a2 - alph2)![]()
![]()
void SMO::smo_main_process()
{
read_in_data(); //initialize
if(!is_test_only)
{
alph.resize(end_support_i,0);
b=0;
error_cache.resize(N);
}
self_dot_product.resize(N);
precomputed_self_dot_product();
if (!is_test_only)
{
numChanged = 0;
examineAll = 1;
while (numChanged > 0 || examineAll)
{
numChanged = 0;
if (examineAll)
{
for (int k = 0; k < N; k++)
numChanged += examineExample (k);
}
else
{
for (int k = 0; k < N; k++)
if (alph[k] != 0 && alph[k] != C)
numChanged += examineExample (k);
}
if (examineAll == 1)
examineAll = 0;
else if (numChanged == 0)
examineAll = 1;
}
}
}
![]()
![]()
![]()
int SMO::examineExample(int i1)
{
float y1, alph1, E1, r1;
y1 = (float)target[i1];
alph1 = alph[i1];
if (alph1 > 0 && alph1 < C)
E1 = error_cache[i1];
else
E1 = learned_func_nonlinear(i1) - y1;
r1 = y1 * E1;
if ((r1 < -tolerance && alph1 < C)||(r1 > tolerance && alph1 > 0))
{
/使用三种方法选择第二个乘子
//1:在non-bound乘子中寻找maximum fabs(E1-E2)的样本
//2:如果上面没取得进展,那么从随机位置查找non-boundary 样本
//3:如果上面也失败,则从随机位置查找整个样本,改为bound样本
if (examineFirstChoice(i1,E1)) return 1; //1
if (examineNonBound(i1)) return 1; //2
if (examineBound(i1)) return 1; //3
}
///没有进展
return 0;
}
![]()
![]()
![]()
//径向基核函数
float SMO::kernel_func(int i,int k)
{
float sum=dot_product_func(i,k);
sum*=-2;
sum+=self_dot_product[i]+self_dot_product[k];
return exp(-sum/two_sigma_squared);
}
float SMO::learned_func_nonlinear(int k)
{
float sum=0;
for(int i=0; i
![]()