python实现井字棋小游戏(使用蒙特卡洛搜索树进行训练)
需要源码请点赞关注收藏后评论区留言或私信博主
蒙特卡洛搜索树是一类算法的统称,它适用于零和且确定环境的游戏,现在用蒙特卡洛搜索树算法对井字棋进行训练。
训练要求将模拟次数设定为2000次,即每个状态都模拟2000次到达终点,到到达胜利叶子节点则回溯得一分,失败或平局则不得分。
代码运行效果如下
部分代码如下
# 深度强化学习——原理、算法与PyTorch实战,代码名称:代31-例8.6-基于蒙特卡洛树的井字棋实例.py
import numpy as np
import sys
import math
import random
# 初始化环境
class environment():
def __init__(self):
self.start_env = np.array([[0] * 3] * 3)
class State(object):
def __init__(self):
self.current_env = [[]]
self.current_value = 0
self.current_round_index = 0
self.cumulative_choices = [[]]
self.available_choice = [[]]
# 定义结束情况
def is_end(self):
tiaojian = True
for i in range(0, 3):
for j in range(0, 3):
if self.current_env[i][j] == 0:
tiaojian = False
for i in range(0, 3):
if (np.array(self.current_env)[i] == np.array([1, 1, 1])).all() or (
np.array(self.current_env)[i] == np.array([2, 2, 2])).all():
tiaojian = True
if (np.array(self.current_env)[:, 0] == np.array([1, 1, 1])).all() or (
np.array(self.current_env)[:, 0] == np.array([2, 2, 2])).all() or (
np.array(self.current_env)[:, 1] == np.array([1, 1, 1])).all() or (
np.array(self.current_env)[:, 1] == np.array([2, 2, 2])).all() or (
np.array(self.current_env)[:, 2] == np.array([1, 1, 1])).all() or (
np.array(self.current_env)[:, 2] == np.array([2, 2, 2])).all():
tiaojian = True
elif np.array(self.current_env)[0, 0] == np.array(self.current_env)[1, 1] == np.array(self.current_env)[
2, 2] != 0:
tiaojian = True
elif np.array(self.current_env)[0, 2] == np.array(self.current_env)[1, 1] == np.array(self.current_env)[
2, 0] != 0:
tiaojian = True
return tiaojian
# 定义自家胜利情况
def i_win(self):
tiaojian = False
for i in range(0, 3):
if ((np.array(self.current_env)[i] == np.array([1, 1, 1])).all()):
tiaojian = True
if (np.array(self.current_env)[:, 0] == np.array([1, 1, 1])).all() or (
np.array(self.current_env)[:, 1] == np.array([1, 1, 1])).all() or (
np.array(self.current_env)[:, 2] == np.array([1, 1, 1])).all():
tiaojian = True
if np.array(self.current_env)[0, 0] == np.array(self.current_env)[1, 1] == np.array(self.current_env)[
2, 2] == 1:
tiaojian = True
if np.array(self.current_env)[0, 2] == np.array(self.current_env)[1, 1] == np.array(self.current_env)[
2, 0] == 1:
tiaojian = True
return tiaojian
# 定义自家失败情况
def i_lose(self):
tiaojian = False
for i in range(0, 3):
if ((np.array(self.current_env)[i] == np.array([2, 2, 2])).all()):
tiaojian = True
if (np.array(self.current_env)[:, 0] == np.array([2, 2, 2])).all() or (
np.array(self.current_env)[:, 1] == np.array([2, 2, 2])).all() or (
np.array(self.current_env)[:, 2] == np.array([2, 2, 2])).all():
tiaojian = True
if np.array(self.current_env)[0, 0] == np.array(self.current_env)[1, 1] == np.array(self.current_env)[
2, 2] == 2:
tiaojian = True
if np.array(self.current_env)[0, 2] == np.array(self.current_env)[1, 1] == np.array(self.current_env)[
2, 0] == 2:
tiaojian = True
return tiaojian
# 设置/获取可用动作
def set_available_choice(self, choice):
self.available_choice = choice
def get_available_choice(self):
return self.available_choice
# 设置/获取当前环境
def get_current_env(self):
return self.current_env
def set_current_env(self, env):
self.current_env = env
# 设置/获取累计奖赏
def get_current_value(self):
return self.current_value
def set_current_value(self, value):
self.current_value = value
def get_current_round_index(self):
return self.current_round_index
def set_current_round_index(self, turn):
self.current_round_index = turn
# 设置/获取累积动作
def get_cumulative_choices(self):
return self.cumulative_choices
def set_cumulative_choices(self, choices):
self.cumulative_choices = choices
# 判断是否结束
def is_terminal(self):
# The round index starts from 1 to max round number
return self.is_end()
# 计算累计奖赏
def compute_reward(self):
return self.current_value
# 随机策略得到下一状态
def get_next_state_with_random_choice(self):
a = np.array([[0] * 3] * 3)
b = [0] * len(self.available_choice)
random_choice = random.choice([choice for choice in self.available_choice])
next_state = State()
next_state.set_current_round_index(self.current_round_index + 1)
next_state.set_cumulative_choices(self.cumulative_choices + [random_choice])
for i in range(0, len(self.available_choice)):
b[i] = self.available_choice[i]
next_state.available_choice = b
next_state.available_choice.remove(random_choice)
if next_state.current_round_index != 0 and next_state.current_round_index % 2 == 0:
for i in range(0, 3):
for j in range(0, 3):
a[i][j] = self.current_env[i][j]
a[random_choice[0]][random_choice[1]] = 1
next_state.set_current_env(a)
if next_state.current_round_index != 0 and next_state.current_round_index % 2 == 1:
for i in range(0, 3):
for j in range(0, 3):
a[i][j] = self.current_env[i][j]
a[random_choice[0]][random_choice[1]] = 2
next_state.set_current_env(a)
if next_state.i_win():
next_state.set_current_value(1)
if next_state.i_lose():
next_state.set_current_value(-0.5)
if next_state.i_lose() != True and next_state.i_win() != True:
next_state.set_current_value(0)
return next_state
def __repr__(self):
return "State: {}, value: {}, choices: {}".format(hash(self), self.current_value,
self.available_choice)
# 建立节点
class Node(object):
def __init__(self):
self.env = [[]]
self.parent = None
self.children = []
self.visit_times = 0
self.quality_value = 0.0
self.state = None
def avanum(self):
num = 0
a = self.get_state().current_env
for i in range(0, 3):
for j in range(0, 3):
if a[i][j] == 0:
num += 1
return num
def set_state(self, state):
self.state = state
def get_state(self):
return self.state
def get_parent(self):
return self.parent
def set_parent(self, parent):
self.parent = parent
def get_children(self):
return self.children
def get_visit_times(self):
return self.visit_times
def set_visit_times(self, times):
self.visit_times = times
def visit_times_add_one(self):
self.visit_times += 1
def get_quality_value(self):
return self.quality_value
def set_quality_value(self, value):
self.quality_value = value
def quality_value_add_n(self, n):
self.quality_value += n
def is_all_expand(self):
return len(self.children) == self.avanum()
def add_child(self, sub_node):
sub_node.set_parent(self)
self.children.append(sub_node)
def __repr__(self):
return "Node: {}, Q/N: {}/{}, state: {}".format(hash(self), self.quality_value, self.visit_times, self.state)
# *************************************
# 搜索树策略
def tree_policy(node):
# Check if the current node is the leaf node
while node.get_state().is_terminal() == False:
if node.is_all_expand():
node_best = best_child(node, True)
else:
# Return the new sub node
sub_node = expand(node)
return sub_node
# Return the leaf node
return node_best
# 默认策略
def default_policy(node):
# Get the state of the game
current_state = node.get_state()
# Run until the game over
while current_state.is_terminal() == False:
# Pick one random action to play and get next state
current_state = current_state.get_next_state_with_random_choice()
final_state_reward = current_state.compute_reward()
return final_state_reward
# 扩展
def expand(node):
tried_sub_node_states = [sub_node.get_state().current_env for sub_node in node.get_children()]
# Check until get the new state which has the different action from others
noin = False
while noin == False:
noin = True
new_state = node.get_state().get_next_state_with_random_choice()
for i in range(0, len(tried_sub_node_states)):
if (new_state.current_env == tried_sub_node_states[i]).all():
noin = False
sub_node = Node()
sub_node.set_state(new_state)
node.add_child(sub_node)
return sub_node
def best_child(node, is_exploration):
# TODO: Use the min float value
best_score = -sys.maxsize
best_sub_node = None
# Travel all sub nodes to find the best one
for sub_node in node.get_children():
# Ignore exploration for inference
if is_exploration:
C = 1 / math.sqrt(2.0)
else:
C = 0.0
# UCB = quality / times + C * sqrt(2 * ln(total_times) / times)
left = sub_node.get_quality_value() / sub_node.get_visit_times()
right = 2.0 * math.log(node.get_visit_times()) / sub_node.get_visit_times()
score = left + C * math.sqrt(right)
if score > best_score:
best_sub_node = sub_node
best_score = score
return best_sub_node
# 回传
def backup(node, reward):
# Update util the root node
while node != None:
# Update the visit times
node.visit_times_add_one()
# Update the quality value
node.quality_value_add_n(reward)
# Change the node to the parent node
node = node.parent
# 蒙特卡洛搜索树算法
def monte_carlo_tree_search(node):
computation_budget = 4000
# Run as much as possible under the computation budget
for i in range(computation_budget):
# 1. Find the best node to expand
expand_node = tree_policy(node)
# 2. Random run to add node and get reward
reward = default_policy(expand_node)
# 3. Update all passing nodes with reward
backup(expand_node, reward)
# N. Get the best next node
best_next_node = best_child(node, False)
a = [[sub_node.quality_value, sub_node.get_state().current_env] for sub_node in node.get_children()]
print(a)
return best_next_node
# *************************************
def main():
# Create the initialized state and initialized node
init_state = State()
init_state.set_current_env(np.array([[0] * 3] * 3))
init_state.set_current_round_index(1)
init_state.set_available_choice([[0, 0], [0, 1], [0, 2], [1, 0], [1, 1], [1, 2], [2, 0], [2, 1], [2, 2]])
init_node = Node()
init_node.state = init_state
init_env = environment()
current_node = init_node
# Set the rounds to play
d = 0
while (current_node.get_state().is_terminal() != True):
if d % 2 == 0:
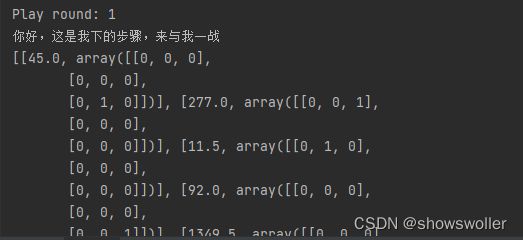
print("Play round: {}".format(d + 1))
print("你好,这是我下的步骤,来与我一战")
current_node = monte_carlo_tree_search(current_node)
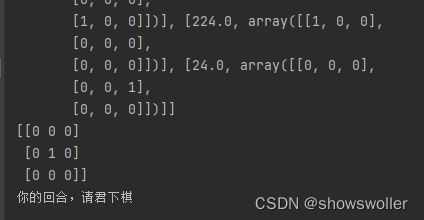
print(current_node.get_state().current_env)
else:
new = Node()
bb = State()
new.set_state(bb)
print("你的回合,请君下棋")
n = 3
a = [[0] * n] * n
for i in range(n):
a[i] = input().split(" ")
for i in range(0, 3):
for j in range(0, 3):
a[i][j] = int(a[i][j])
= current_node.get_state().current_round_index + 1
current_node = new
d += 1
if current_node.get_state().i_win():
print("我赢了!你真菜")
if current_node.get_state().i_lose():
print("我输了,快给我调力度")
if current_node.get_state().i_win() != True and current_node.get_state().i_lose() != True:
print("平局,你还不错")
if __name__ == "__main__":
main()