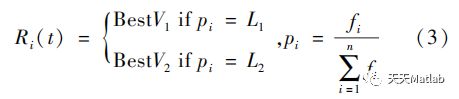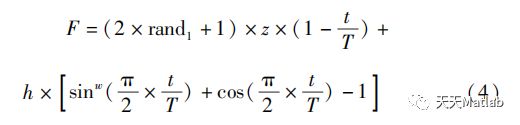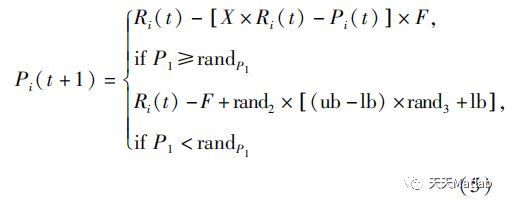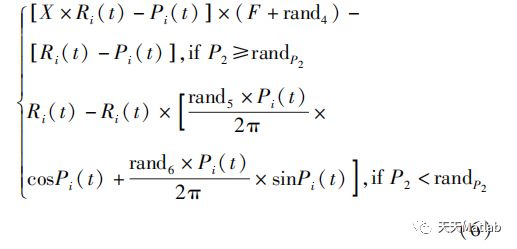基于对立非洲秃鹫优化算法求解单目标优化问题(OAVOA)含Matlab代码
✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
个人主页:Matlab科研工作室
个人信条:格物致知。
更多Matlab仿真内容点击
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机
⛄ 内容介绍
非洲秃鹫优化算法(AVOA)是AbdollahzadehB等[12]于2021年受非洲秃鹫觅食和导航行为启发而提出的一种新型元启发式优化算法,具有寻优能力强、收敛速度快等优点。AVOA是受非洲秃鹫觅食和导航行为启发提出的一种元启发式优化算法。AVOA数学描述如下。
a)确定最佳秃鹫。AVOA通过计算种群所有秃鹫适应度,选择最优和次优适应度对应的秃鹫作为最优秃鹫和次优秃鹫位置,其他秃鹫利用式(3)向最优和次优秃鹫移动。
式中Ri(t)—除最优、次优秃鹫外的其他秃鹫位置;BestV1、BestV2—最优秃鹫和次优秃鹫位置;L1、L2—介于0和1之间待测量参数,其和为1;pi—选择最佳秃鹫的概率;fi—其他秃鹫适应度;t—当前迭代次数;其他参数意义同上。
b)秃鹫饱食率。秃鹫经常觅食,若它们处于饱食状态,则拥有较高能量,这使得它们可以在更广阔的区域觅食;若处于饥饿状态,则没有足够的能量飞行和在更强壮的秃鹰附近觅食。饱食率数学描述为:
式中F—秃鹫饱食率;T—最大迭代次数;z—-1和1之间的随机数;h—-2和2之间的随机数;rand1—0和1之间的随机数;w—控制勘探过程参数,随着w值增大,算法进入勘探阶段的概率增大,反知概率减小。
c)探索阶段。秃鹫具有很高的视觉能力和较好的觅食能力。在AVOA中,秃鹫通过式(5)随机搜寻不同区域。
式中Pi(t+1)—第t+1次迭代秃鹫位置;Pi(t)—第t次迭代秃鹫位置;X—秃鹫随机移动的地方,以保护食物免受其他秃鹫夺取,X=2×rand,rand表示0和1之间的随机数;P1—探索阶段选择参数;rand2、rand3、randP1—0和1之间的随机数;ub、lb—搜索空间上、下限值;其他参数意义同上。
d)开发阶段。AVOA中,开发阶段分为开发一阶段和开发二阶段2种策略,并通过开发阶段选择参数P2、P3决定采用何种策略进行位置更新。开发第一阶段秃鹫位置更新描述如下:
式中rand4、rand5、rand6、randP2—0和1之间的随机数;P2—开发第一阶段更新策略选择参数;其他参数意义同上。
开发第二阶段秃鹫位置更新描述如下:
式中BestV1(t)、BestV2(t)—第t次迭代最优、次优秃鹫位置;randP3—0和1之间的随机数;P3—开发第二阶段更新策略选择参数;Levy(d)—随即游走,其每一步方向完全随机而各向同性,步长为重尾分布;其他参数意义同上。
⛄ 部分代码
% Opposition African Vultures Optimization Algorithm (OAVOA) version 1.0
% B. Jena, M. K. Naik, R. Panda, and A. Abraham,
% 鈥淎 novel minimum generalized cross entropy-based multilevel segmentation
% technique for the brain MRI/Dermoscopic images,鈥�Comput. Biol. Med., p. 106214, 2022,
% doi: https://doi.org/10.1016/j.compbiomed.2022.106214.
%_____________________________________________________________________________________________________
clearvars
close all
clc
disp('OAVOA is tracking the problem');
N=30; % Number of slime mould
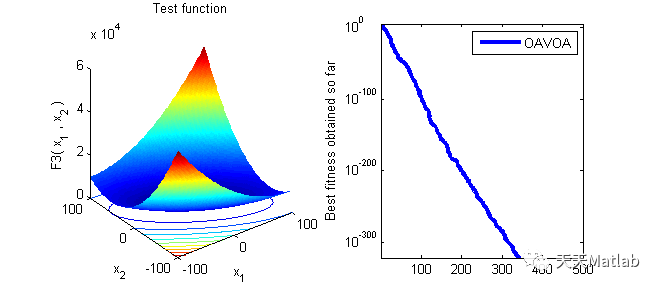
Function_name='F3'; % Name of the test function that can be from F1 to F23
MaxIT=500; % Maximum number of iterations
[lb,ub,dim,fobj]=Get_Functions_details(Function_name); % Function details
Times=21; %Number of independent times you want to run the OAVOA
display(['Number of independent runs: ', num2str(Times)]);
for i=1:Times
[Destination_fitness(i),bestPositions(i,:),Convergence_curve(i,:)]=OAVOA(N,MaxIT,lb,ub,dim,fobj);
display(['The optimal fitness of OAVOA is: ', num2str(Destination_fitness(i))]);
end
[bestfitness,index]=min(Destination_fitness);
disp('--------Best Fitness, Average Fitness, Standard Deviation and Best Solution--------');
display(['The best fitness of OAVOA is: ', num2str(bestfitness)]);
display(['The average fitness of OAVOA is: ', num2str(mean(Destination_fitness))]);
display(['The standard deviation fitness of OAVOA is: ', num2str(std(Destination_fitness))]);
display(['The best location of OAVOA is: ', num2str(bestPositions(index,:))]);
figure('Position',[284 214 660 290])
%Draw search space
subplot(1,2,1);
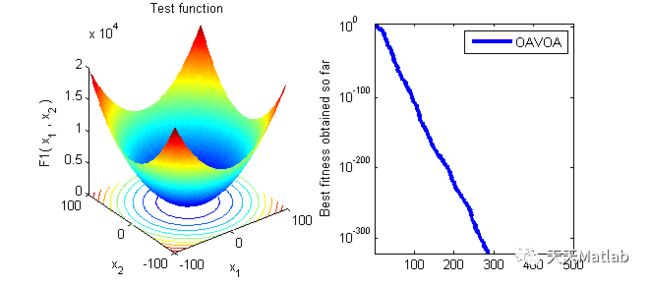
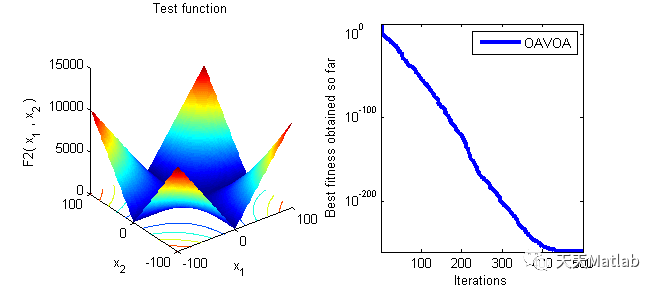
func_plot(Function_name);
title('Test function')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
grid off
%Draw objective space
subplot(1,2,2);
semilogy(Convergence_curve(index,:),'LineWidth',3);
xlabel('Iterations');
ylabel('Best fitness obtained so far');
legend('OAVOA');
box on;
axis tight;
grid off;
⛄ 运行结果
⛄ 参考文献
[1] Chastikova V A , Ostapov D S . HYBRID OPTIMIZING GRIFFON-VULTURE ALGORITHM BASED ON SWARM INTELLIGENCE MECHANISMS[J]. Polythematic Online Scientific Journal of Kuban State Agrarian University, 2014(100).
❤️ 关注我领取海量matlab电子书和数学建模资料
❤️部分理论引用网络文献,若有侵权联系博主删除