一种改进的鲸鱼优化算法-附代码

一种改进的鲸鱼优化算法

摘要： 针对鲸鱼优化算法( whale optimization algorithm，WOA) 容易陷入局部最优和收敛精度低的问题进行了研究，提出一种改进的鲸鱼优化算法( IWOA) 。该算法通过准反向学习方法来初始化种群，提高种群的多样性;然后将线性收敛因子修改为非线性收敛因子，有利于平衡全局搜索和局部开发能力; 另外，通过增加自适应权重改进鲸鱼优化算法的局部搜索能力，提高收敛精度; 最后，通过随机差分变异策略及时调整鲸鱼优化算法，避免陷入局部最优。

1.鲸鱼优化算法

基础鲸鱼算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/107559167

2. 改进鲸鱼优化算法

2.1 准反向学习初始化种群

Gondro 等人 ${}^{[8]}$ 指出高质量的初始化种群对算法的求解精 度和收敛速度等性能有很大的帮助。然而, 基本的鲸鱼优化算 法采用的是随机初始化的方法, 该方法随机性很大, 不能保证 初始种群的多样性。为了保证初始化种群的多样性, 采用了反 向学习的改进方法, 即准反向学习来初始化种群。
反向学习 ${}^{[6,9,10]}$ 是在明确变量的范围边界, 通过按照一定 的规则来求其对应的反向解, 其详细内容如下:
假设鲸鱼种群的规模为 $N$, 搜索空间为 $d$ 维, 第 $i$ 只鲸鱼 在第 $d$ 维空间中的位置可以表示为 ${\mathbf{X}}_i=\left(x_i^1,x_i^2,\cdots ,x_i^d\right)(i=1$, $2,\cdots ,N),x_i^j\in \left[a_i^j,b_i^j\right](j=1,2,\cdots ,d),a_i^j$ 和 $b_i^j$ 分别表示 $x_i^j$ 的 下界和上界,其对应反向解如下:
$${\hat{x}}_i^j=a_i^j+b_i^j-x_i^j\text{\hspace{1em}(7)}$$
在实际应用中, 反向解的效果并不一定很好, 本文为了解 决这一问题采用了准反向解的方法, 该方法可以根据式 (7) 演 变得到：
$$\widehat{x_i^j}=\{\begin{array}{ll}\mathrm{rand}\left({\mathrm{avg}}_i^j,{\hat{x}}_i^j\right)& x_i^j⩽{\mathrm{avg}}_i^j\\ \mathrm{rand}\left({\hat{x}}_i^j,{\mathrm{avg}}_i^j\right)& x_i^j>{\mathrm{avg}}_i^j\end{array}\text{\hspace{1em}(8)}$$
其中: ${\mathrm{avg}}_i^j=\frac{b_i^j-a_i^j}{2};(a,b)$ 代表在 $a、b$ 之间的随机数。
随机产生的 $N$ 个初始个体和准反向学习 ${}^{[9]}$ 求得的 $N$ 个准 反向解将其合并, 然后通过一种种群多样性最大化的篮选机 制, 从这 $2N$ 个个体中选择种群多样性最大化的 $N$ 个个体。
为了使种群获得比较好的初始化种群, 本文将随机解与其 对应的准反向解进行取优化处理, 这样既保证了种群的多样性, 同时又能使种群较快地收敛到全局最优解。其数学模型如下:
$$\text{ fit }(X)>\text{ fit }(\stackrel{\vee }{V})?X,\stackrel{V}{X}\text{\hspace{1em}(9)}$$
其中: fit 为适应度函数; $X$ 和 $X$ 分别表示随机产生的个体和准 反向学习产生的个体。

2.2 非线性收敛因子

与其他群体智能优化算法类似, 鲸鱼优化算法在寻优过程 中同样会遇到全局搜索能力和局部开发能力不平衡的现象。 在基本鲸鱼优化算法中, 其掌握鲸鱼进行全局搜索还是局部搜 索的是参数 $|A|$, 当参数 $|A|⩾1$ 时, 算法以 $0.5$ 的概率进行随 机全局搜索, 当 $|A|<1$ 时, 算法进行局部开发。由于收玫因子 $a$ 进行线性变化并不能很好地调节全局搜索能力和局部开发 能力, 因此本文提出来一种非线性收敛因子 ${}^{[5,11,12]}$ 为
$$a=2-2\sin \left(\mu \frac{t}{ma{x}_{i}ter}\pi +\phi \right)\text{\hspace{1em}(10)}$$
其中: max_iter 为最大迭代次数; $t$ 为当前迭代次数; $\mu$ 和 $\phi$ 是其 表达式相关参数, 选取 $\mu =\frac{1}{2},\phi =0$ 。

2.3 自适应权重策略与随机差分法变异策略

鲸鱼优化算法在后期局部开发时易陷入局部最优, 出现早 熟收敛的现象, 为了使算法能够保持种群的多样性并且能够及 时跳出局部最优, 提出来一种自适应权重策略和随机差分变异策略
自适应权重策略数学表达式如下:
$$\omega =1-\frac{e^{\frac{t}{\max \text{ iter }}-1}}{e-1},\mathbf{X}(t+1)=\omega \cdot {\mathbf{X}}_p(t)-\mathbf{A}\cdot \mathbf{D}\text{\hspace{1em}(11)}$$

$$\mathbf{X}(t+1)=\omega \cdot {\mathbf{X}}_p(t)+\mathbf{D}\cdot e^{bl}\cdot \cos (2\pi l)\text{\hspace{1em}(12)}$$

随机差分变异策略如下:
$$\mathbf{X}(t+1)=r_1\times \left({\mathbf{X}}_p(t)-\mathbf{X}(t)\right)+r_2\times \left({\mathbf{X}}^{\prime }(t)-\mathbf{X}(t)\right)\text{\hspace{1em}(13)}$$
其中: $r_1$ 和 $r_2$ 为 $[0,1]$ 的随机数, $X^{\prime }(t)$ 为种群中随机选取的个体。
每个个体都要经过包围捕食、螺旋更新、搜索猎物阶段, 当 个体进行包围捕食或螺旋更新时采用自适应权重策略去更新位置，之后个体需要通过随机差分变异策略对其再次更新，取其变化前后的最优位置，加快了种群的收敛，有效地防止了种群陷入局部最优。种群通过这两种策略协同工作，使得算法具有更好的寻优效果。

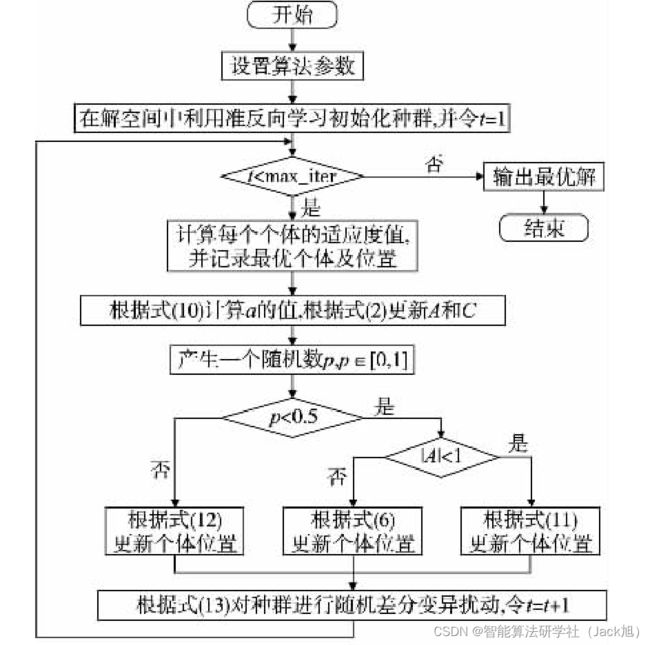
3.实验结果

4.参考文献

[1]武泽权,牟永敏.一种改进的鲸鱼优化算法[J].计算机应用研究,2020,37(12):3618-3621.

5.Matlab代码

6.Python代码