题目描述
这是 LeetCode 上的 908. 最小差值 I ,难度为 中等。
Tag : 「数学」、「单调栈」
给定一个整数数组 arr,找到 min(b) 的总和,其中 b 的范围为 arr 的每个(连续)子数组。
由于答案可能很大,因此 返回答案模 $10^9 + 7$ 。
示例 1:
输入:arr = [3,1,2,4]
输出:17
解释:
子数组为 [3],[1],[2],[4],[3,1],[1,2],[2,4],[3,1,2],[1,2,4],[3,1,2,4]。
最小值为 3,1,2,4,1,1,2,1,1,1,和为 17。示例 2:
输入:arr = [11,81,94,43,3]
输出:444提示:
- $1 <= arr.length <= 3 \times 10^4$
- $1 <= arr[i] <= 3 \times 10^4$
单调栈 + 数学
原题解链接在 这里,本次增加了更为详细的细节说明。
原问题为求所有子数组的最小值之和。
统计所有子数组需要枚举左右端点,复杂度为 $O(n^2)$,对于每个子数组,我们还需要通过线性扫描的方式找到其最小值,复杂度为 $O(n)$,因此朴素解法的整体复杂度为 $O(n^3)$,题目给定数据范围为 $3 \times 10^4$,会 TLE。
由于我们是从子数组中取最小值来进行累加,即参与答案构成的每个数必然某个具体的 $arr[i]$。
因此我们可以将原问题转化为「考虑统计每个 $arr[i]$ 对答案的贡献」。
对于某一个 $arr[i]$ 而言,我们考虑其能够作为哪些子数组的最小值。
我们可以想象以 $arr[i]$ 为中心,分别往两端进行拓展,只要新拓展的边界不会改变「$arr[i]$ 为当前子数组的最小值」的性质即可。
换句话说,我们需要找到 $arr[i]$ 作为最小值的最远左右边界,即找到 $arr[i]$ 左右最近一个比其小的位置 l 和 r。
在给定序列中,找到任意 $A[i]$ 最近一个比其大/小的位置,可使用「单调栈」进行求解。
到这里,我们会自然想到,通过单调栈的方式,分别预处理除 l 和 r 数组:
l[i] = loc含义为下标i左边最近一个比arr[i]小的位置是loc(若在 $arr[i]$ 左侧不存在比其小的数,则loc = -1)r[i] = loc含义为下标i右边最近一个比arr[i]大的位置是loc(若在 $arr[i]$ 左侧不存在比其大的数,则loc = n)
当我们预处理两数组后,通过简单「乘法原理」即可统计以 $arr[i]$ 为最小值时,子数组的个数:
- 包含 $arr[i]$ 的子数组左端点个数为 $a = i - l[i]$ 个
- 包含 $arr[i]$ 的子数组右端点个数为 $b = r[i] - i$ 个
子数组的个数 $\times$ 子数组最小值 $arr[i]$,即是当前 $arr[i]$ 对答案的贡献:$a \times b \times arr[i]$。
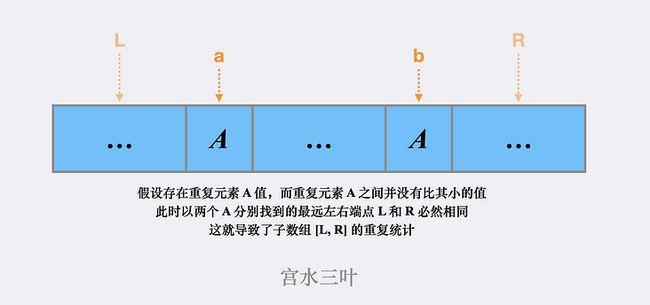
统计所有 $arr[i]$ 对答案的贡献即是最终答案,但我们忽略了「当 arr 存在重复元素,且该元素作为子数组最小值时,最远左右端点的边界越过重复元素时,导致重复统计子数组」的问题。
我们不失一般性的举个 来理解(下图):
为了消除这种重复统计,我们可以将「最远左右边界」的一端,从「严格小于」调整为「小于等于」,从而实现半开半闭的效果。
Java 代码:
class Solution {
int MOD = (int)1e9+7;
public int sumSubarrayMins(int[] arr) {
int n = arr.length, ans = 0;
int[] l = new int[n], r = new int[n];
Arrays.fill(l, -1); Arrays.fill(r, n);
Deque d = new ArrayDeque<>();
for (int i = 0; i < n; i++) {
while (!d.isEmpty() && arr[d.peekLast()] >= arr[i]) r[d.pollLast()] = i;
d.addLast(i);
}
d.clear();
for (int i = n - 1; i >= 0; i--) {
while (!d.isEmpty() && arr[d.peekLast()] > arr[i]) l[d.pollLast()] = i;
d.addLast(i);
}
for (int i = 0; i < n; i++) {
int a = i - l[i], b = r[i] - i;
ans += a * 1L * b % MOD * arr[i] % MOD;
ans %= MOD;
}
return ans;
}
} TypeScript 代码:
const MOD = 1000000007
function sumSubarrayMins(arr: number[]): number {
let n = arr.length, ans = 0
const l = new Array(n).fill(-1), r = new Array(n).fill(n)
const stk = new Array(n).fill(0)
let he = 0, ta = 0
for (let i = 0; i < n; i++) {
while (he < ta && arr[stk[ta - 1]] >= arr[i]) r[stk[--ta]] = i
stk[ta++] = i
}
he = ta = 0
for (let i = n - 1; i >= 0; i--) {
while (he < ta && arr[stk[ta - 1]] > arr[i]) l[stk[--ta]] = i
stk[ta++] = i
}
for (let i = 0; i < n; i++) {
const a = i - l[i], b = r[i] - i
ans += a * b % MOD * arr[i] % MOD
ans %= MOD
}
return ans
} Python 代码:
class Solution:
def sumSubarrayMins(self, arr: List[int]) -> int:
n, ans = len(arr), 0
l, r = [-1] * n, [n] * n
stk = []
for i in range(n):
while stk and arr[stk[-1]] >= arr[i]:
r[stk.pop()] = i
stk.append(i)
stk = []
for i in range(n - 1, -1, -1):
while stk and arr[stk[-1]] > arr[i]:
l[stk.pop()] = i
stk.append(i)
for i in range(n):
a, b = i - l[i], r[i] - i
ans += a * b * arr[i]
return ans % (10 ** 9 + 7)- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
优化
实际上,当我们从栈中弹出某个 $arr[cur]$ 时,其右边界必然是导致其弹出的 arr[r](当前所遍历到的元素),而 $arr[cur]$ 若存在左边界,必然是位于 $cur$ 栈中的前一位置,即 $arr[cur]$ 弹出后的新栈顶元素(若不存在物理左边界,则左边界为 $-1$)。
Java 代码:
class Solution {
int MOD = (int)1e9+7;
public int sumSubarrayMins(int[] arr) {
int n = arr.length, ans = 0;
Deque d = new ArrayDeque<>();
for (int r = 0; r <= n; r++) {
int t = r < n ? arr[r] : 0;
while (!d.isEmpty() && arr[d.peekLast()] >= t) {
int cur = d.pollLast();
int l = d.isEmpty() ? -1 : d.peekLast();
int a = cur - l, b = r - cur;
ans += a * 1L * b % MOD * arr[cur] % MOD;
ans %= MOD;
}
d.addLast(r);
}
return ans;
}
} TypeScript 代码:
const MOD = 1000000007
function sumSubarrayMins(arr: number[]): number {
let n = arr.length, ans = 0
const stk = new Array(n).fill(0)
let he = 0, ta = 0
for (let r = 0; r <= n; r++) {
const t = r < n ? arr[r] : 0
while (he < ta && arr[stk[ta - 1]] >= t) {
const cur = stk[--ta]
const l = he < ta ? stk[ta - 1] : -1
const a = cur - l, b = r - cur
ans += a * b % MOD * arr[cur] % MOD
ans %= MOD
}
stk[ta++] = r
}
return ans
} Python 代码:
class Solution:
def sumSubarrayMins(self, arr: List[int]) -> int:
n, ans = len(arr), 0
stk = []
for r in range(n + 1):
t = arr[r] if r < n else 0
while stk and arr[stk[-1]] >= t:
cur = stk.pop()
l = stk[-1] if stk else -1
a, b = cur - l, r - cur
ans += a * b * arr[cur]
stk.append(r)
return ans % (10 ** 9 + 7)- 时间复杂度:$O(n)$
- 空间复杂度:$O(n)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.907 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSou... 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地
本文由mdnice多平台发布