《机器学习与应用》实验一
文章目录
- Python环境配置
-
- Anaconda
- DataSpell
-
- 使用DataSpell查看代码中的变量的值
- Python基础语法
-
- 编码:
- 计算:
- 判断:
- 变量:
- 标识符:
- Python 保留字:
- 注释:
- print 与 input:
- 查看包、方法、变量的使用说明:
- 缩进:
- 多行语句:
- 导入包:
- 画图:
- 控制流(for、while 和 if):
- 使用Python理解梯度下降
Python环境配置
Anaconda
Anaconda安装及入门教程
DataSpell
安装Jetbrains Toolbox,然后在Toolbox中找到DataSpell点击安装
打开DataSpell后,在设置中找到插件,然后在市场中搜索Chinese,安装中文语言包

新建一个工作区目录,比如我新建了一个叫Lab1的工作区目录
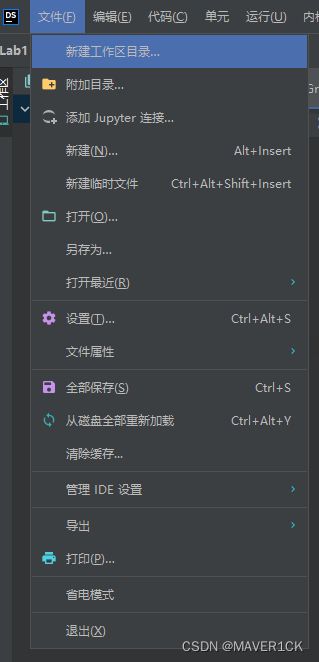
右键新建的工作区目录,如图所示新建Python文件,就可以写代码了
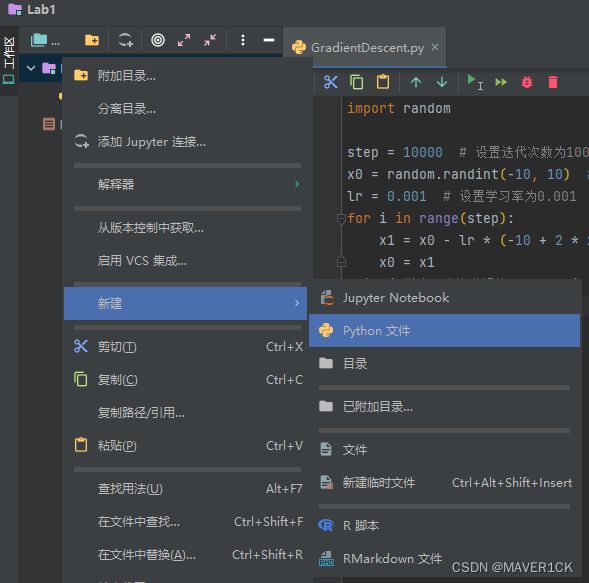
使用DataSpell查看代码中的变量的值
代码写好后,右键自己的代码空白处,点击“在控制台中执行单元”

点击这个眼镜图标,就能看到自己代码中的变量了

Python基础语法
编码:
默认 UTF-8 编码
计算:
- 符号:+、-、*、/、**、//、%、abs、round(3.1425,2)
含义:加、减、乘、除、幂、取整、取余、取绝对值、保留 2 位小数 - 特殊的:+=、-=、*=、、/=、//=、%=
含义:如果 a=a+b,那么 a+=b
判断:
- 符号:>、<、==、!=、>=、<=、and、or、not
含义:大于、小于、等于、不等于、大于等于、小于等于,且、或、非
变量:
- 类型有:整数、浮点数、字符串、列表、元组、字典和逻辑运算符
标识符:
- 第一个字符必须为字母或者下划线,其余部分可以为字母、数字和下划线。注意标识符对大小写敏感。
Python 保留字:
- 不能用它来做标识符,它们各自有各自的含义。比如 True、if、else,是不能拿来做变量或者函数名的。
查找当前版本的保留字:输入 import keyword,然后输入 keyword.kwlist ,便可。
注释:
- 单行注释用#开头,此行#后的所有字符不被运行。
- 多行注释有三种方法。
- 一:每行前面输入#
快捷方式为,选中所需要注释的行,同时按 Ctrl+1(再按一次表示取消注释),或者按 Ctrl+4,进行块注释,按 Ctrl+5,取消块注释; - 二:三个单引号,例如’‘‘多行注释内容’’’
- 三:三个双引号,例如"““多行注释内容””"
- 一:每行前面输入#
print 与 input:
- 输出用 print( ),输入用 input( )
练习:询问对方名字,并问好
friends = ['zw', 'ld', 'fy', 'yy']
for i in friends:
print('hello! ' + i)
print('Done')
查看包、方法、变量的使用说明:
help(object) 或者在 help 窗口输入所需了解的对象
缩进:
- python 使用缩进(空格和制表符)来决定逻辑行的层次,从而用来决定语句的分组。
缩进的空格数可变,但是同一个代码块的语句必须包含相同的缩进,一般为 4个空格或一个 tab 键(注意同一个 py 文件里不要混合使用 tab 或四个空格,否则跨平台工作时会报错,建议选择一种方式一直使用)。
如:输出数字 1 到 5
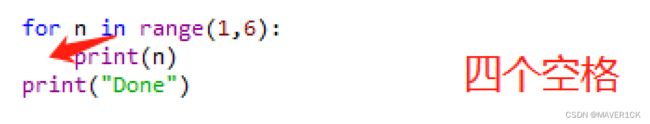
多行语句:
- 若语句很长,一行写不完,则可以用反斜杠(\)来实现多行语句,如:
item_one = 1
item_two = 2
Total = item_one + \
item_two
- 但是在[],{},()中的多行语句,不需要使用反斜杠(\),直接换行即可。
导入包:
- 使用 import 或者 from…import
将整个包导入,格式为:import somemodule
从某个包导入某个函数,格式为:from somemodule import somefunction
从某个包导入多个函数,格式为:from somemodule import func1,func2,func3
从某个包导入全部函数,格式为:from somemodule import *
注意:如果安装好了所需要的包,那么在这里导入的时候不会报错,如果报错了,说明此包需要先安装。
画图:
- 在控制台输出结果需要加命令:%matplotlib inline
- 在新窗口输出结果需要加命令:%matplotlib qt5
控制流(for、while 和 if):
- for 循环
# 问好
friends = ['zw', 'ld', 'fy', 'yy']
for i in friends:
print('hello! ' + i)
print('Done')
- while 循环
# 求和
num = 1
sum_num = 0
while num < 11:
print(num)
sum_num += num
num += 1
print("sum_num = ", sum_num)
- if 判断结构
# 判断奇偶数
n = input("请输入一个整数:")
n = int(n)
if n % 2 == 0:
print("这是一个偶数")
else:
print("这是一个奇数")
使用Python理解梯度下降
梯度下降法在统计学习还是深度学习中都得到了广泛的应用,我们通过构建合理的模型,将模型预测的输出和正确结果进行误差计算,通过优化模型参数使得输出的结果和正确结果的误差最小,我们往往会把误差损失函数构建成一个凸函数,这样使得参数的求解比较单一化,就像一元二次函数只有一个波峰或者波谷,那么求解答案就是寻找这个波峰或者波谷,如果把误差损失函数表达成类似sinx的函数,存在多个波峰波谷,那么求解的答案就会有多个,显然求解的众多个答案并非都是最优解。
我们现在来解释梯度下降法,以一个一元二次函数举例。
y = x 2 − 10 y=x^2-10 y=x2−10
画图如下:
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-10, 20, 0.01)
y = x * x - 10 * x
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x, y)
plt.show()
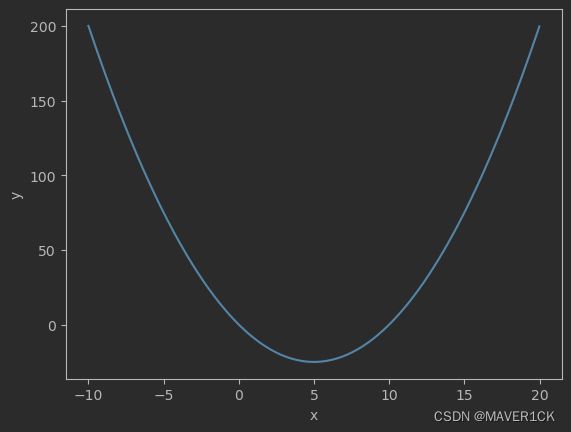
假设这个表示我们模型的损失函数,现在我们的波谷,就是我们模型误差最小的参数点,此时认为x就是我们未知的参数,如何寻找x取值为多少才能达到这个波谷呢?
这就需要用到梯度下降法。
我们先对关于x的函数y求关于x的导函数,得到为
d y = 2 x − 10 dy=2x-10 dy=2x−10
于是我们初始化x为一个随机值a
x = a x=a x=a
然后不断迭代下面的过程
x 1 = x 0 − d y = x 0 − l r ∗ ( − 10 + 2 ∗ x 0 ) x1=x0-dy=x0-lr*(-10+2*x0) x1=x0−dy=x0−lr∗(−10+2∗x0)
x 0 = x 1 x0=x1 x0=x1
上面的lr为学习率,也叫步长,意思为每次x更新变动的数据大小。因为这是一个不断迭代的过程,我们有两种方法让这个迭代结束:
- 一种是设置误差方法,让这个误差小于某个阈值就结束,当然这种方法容易陷入死循环,因为你无法判断一个模型最终拟合的数据误差有多大
- 第二种方法就是设置迭代次数,这也是比较合理的目前为止深度学习还是机器学习都比较常用的迭代结束判断条件。
现在解释下上面的迭代函数为啥可以找到这个波谷的近似位置,原因是:
- 比如在波谷右边,波谷右边的函数曲线上的任意点斜率dy大于0,此时x1=x0-lrdy,会让点x向左移,直到找到左边的波谷位置
- 如果在波谷左边,波谷左边的函数曲线斜率dy小于0,那么x1=x0-lrdy,就会使得x数值增大,位置向右移,不断移动找到右边的波谷位置。
先利用我们的一元二次函数顶点公式求解出顶点的x=5,现在利用梯度下降法去找一下这个结果是否和我们的标准结果一致。
import random
step = 10000 # 设置迭代次数为10000
x0 = random.randint(-10, 10) # 随机初始化一个数值
lr = 0.001 # 设置学习率为0.001
for i in range(step):
x1 = x0 - lr * (-10 + 2 * x0) # 梯度下降迭代
x0 = x1
print('梯度下降法求解结果:', x0)