模型评估——混淆矩阵confusion_matrix

 

本篇文章我们讲一个评估方法，混淆矩阵（confusion_matrix ）

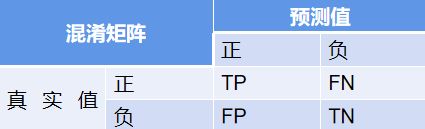
混淆矩阵定义及表示含义  ：

混淆矩阵以矩阵形式将数据集中的记录按照真实的类别与分类模型预测的类别判断两个标准进行汇总。其中矩阵的行表示真实值，矩阵的列表示预测值。

TP（True Positive）: 将正类预测为正类数 即正确预测，真实为0，预测也为0

FN （False Negative）：将正类预测为负类 即错误预测，真实为0，预测为1

FP（False Positive）：将负类预测为正类数 即错误预测， 真实为1，预测为0

TN （True Negative）：将负类预测为负类数，即正确预测，真实为1，预测也为1

 

四种评估方式：

精确率Precision=TP / (TP+FP), 在预测是Positive所有结果中，预测正确的比重

召回率recall=TP / (TP+FN), 在真实值为Positive的所有结果中，预测正确的比重

准确率accuracy=(TP+TN)  / (TP+FN+FP+TN) 所有预测为正确结果所占总预测值的比重

特异度Specificity = TN / （TN+FP） 在真实值是Negative的所有结果中，预测正确的比重

可以看到准确率中的分子值就是矩阵对角线上的值。

 

下面我们先以二分类为例，看下矩阵表现形式，如下：

现在我们举个列子，并画出混淆矩阵表，假如宠物店有10只动物，其中6只狗，4只猫，现在有一个分类器将这10只动物进行分类，

分类结果为5只狗，5只猫（5=1+4。），那么我们画出分类结果混淆矩阵，并进行分析，

 

通过混淆矩阵我们可以轻松算的真实值狗的数量（行数量相加）为6=5+1，

分类得到狗的数量（列数量相加）为5=5+0,真实猫的数量为4=0+4，

以狗为例：

Precision（狗）：5 / 5 =100%     

recall （狗）：5 / 6 =  83.3%

accuracy ：9 / 10 = 90%

Specificity ：4 / 4 = 100%

 

 

那么对于多分类问题来说：

 

与二分类混淆矩阵一样，矩阵行数据相加是真实值类别数，列数据相加是分类后的类别数，那么相应的就有以下计算公式;

精确率_狗= 5 / 6 = 83.3%

召回率_狗 = 5 / 9 = 55.5%

 

通用做法：

 

 

与二分类混淆矩阵一样，矩阵行数据相加是真实值类别数，列数据相加是分类后的类别数，那么相应的就有以下计算公式;

精确率_类别1=a/(a+d+g)

召回率_类别1=a/(a+b+c)

 

混淆矩阵代码：

 

from sklearn.metrics import confusion_matrix
from sklearn.metrics import recall_score
import matplotlib.pyplot as plt
 
 
# 预测数据，predict之后的预测结果集
guess = [1, 0, 1, 2, 1, 0, 1, 0, 1, 0]
# 真实结果集
fact = [0, 1, 0, 1, 2, 1, 0, 1, 0, 1]
# 类别
classes = list(set(fact))
# 排序，准确对上分类结果
classes.sort()
# 对比，得到混淆矩阵
confusion = confusion_matrix(guess, fact)
# 热度图，后面是指定的颜色块，gray也可以，gray_x反色也可以
plt.imshow(confusion, cmap=plt.cm.Blues)
# 这个东西就要注意了
# ticks 这个是坐标轴上的坐标点
# label 这个是坐标轴的注释说明
indices = range(len(confusion))
# 坐标位置放入
# 第一个是迭代对象，表示坐标的顺序
# 第二个是坐标显示的数值的数组，第一个表示的其实就是坐标显示数字数组的index，但是记住必须是迭代对象
plt.xticks(indices, classes)
plt.yticks(indices, classes)
# 热度显示仪？就是旁边的那个验孕棒啦
plt.colorbar()
# 就是坐标轴含义说明了
plt.xlabel('guess')
plt.ylabel('fact')
# 显示数据，直观些
for first_index in range(len(confusion)):
    for second_index in range(len(confusion[first_index])):
        plt.text(first_index, second_index, confusion[first_index][second_index])
 
# 显示
plt.show()
 
# PS:注意坐标轴上的显示，就是classes
# 如果数据正确的，对应关系显示错了就功亏一篑了
# 一个错误发生，想要说服别人就更难了from sklearn.metrics import confusion_matrix
from sklearn.metrics import recall_score
import matplotlib.pyplot as plt
 
 
# 预测数据，predict之后的预测结果集
guess = [1, 0, 1, 2, 1, 0, 1, 0, 1, 0]
# 真实结果集
fact = [0, 1, 0, 1, 2, 1, 0, 1, 0, 1]
# 类别
classes = list(set(fact))
# 排序，准确对上分类结果
classes.sort()
# 对比，得到混淆矩阵
confusion = confusion_matrix(guess, fact)
# 热度图，后面是指定的颜色块，gray也可以，gray_x反色也可以
plt.imshow(confusion, cmap=plt.cm.Blues)
# 这个东西就要注意了
# ticks 这个是坐标轴上的坐标点
# label 这个是坐标轴的注释说明
indices = range(len(confusion))
# 坐标位置放入
# 第一个是迭代对象，表示坐标的顺序
# 第二个是坐标显示的数值的数组，第一个表示的其实就是坐标显示数字数组的index，但是记住必须是迭代对象
plt.xticks(indices, classes)
plt.yticks(indices, classes)
# 热度显示仪？就是旁边的那个验孕棒啦
plt.colorbar()
# 就是坐标轴含义说明了
plt.xlabel('guess')
plt.ylabel('fact')
# 显示数据，直观些
for first_index in range(len(confusion)):
    for second_index in range(len(confusion[first_index])):
        plt.text(first_index, second_index, confusion[first_index][second_index])
 
# 显示
plt.show()
 
# PS:注意坐标轴上的显示，就是classes
# 如果数据正确的，对应关系显示错了就功亏一篑了
# 一个错误发生，想要说服别人就更难了