机器学习 逻辑回归(1)二分类
机器学习 逻辑回归之二分类
- 一、前言
- 二、sigmoid函数
- 三、假设函数
- 四、代价函数
- 五、梯度下降
- 六、二分类原生代码实现
-
- 6.1 生成模拟数据
- 6.2 添加前置与数据分割
- 6.3 迭代训练
- 6.4 验证数据
- 七、sklearn代码实现
一、前言
机器学习 单变量线性回归 (1)背景介绍
梯度下降法解单元函数
向量微积分——理解梯度
机器学习 单变量线性回归 (2)梯度下降法
机器学习 单变量线性回归 (3)代码实现
机器学习 多变量线性回归
前面一系列文章介绍了线性回归,接下来介绍逻辑回归。
线性回归的结果可能是一个区间范围内的任意值,例如预测房价,结果可能是100,100.5,100.6等。
逻辑回归用于解决分类问题,例如识别一张图片是否有猫,识别手写数字是几、判断一件商品是什么类型等,预测结果是逻辑值,0或1(2,3,…n),是或否。
二分类属于只有两种结果的逻辑回归。
逻辑回归与线性回归的区别,类似于数字电路与模拟电路的区别。
比如说,数字电路的电压抽象成0和1,例如最高电压为5V,设定0~2.5V为0,而2.5~5V为1;
而模拟电路则可以是0~5V的任意值,比如温度传感器的结果,用0和1来表示温度显然是不够的,那么我们可以通过0~5V的结果映射成0~50℃来知道具体的温度(可以是小数点后n位)。
二、sigmoid函数
sigmoid函数也叫Logistic函数,它可以将一个实数映射到(0,1)的区间。
函数表示如下 g ( x ) = 1 1 + e − x g(x)=\frac1{1+e^{-x}} g(x)=1+e−x1
其导数为 g ′ ( x ) = g ( x ) ( 1 − g ( x ) ) g'(x)=g(x)(1-g(x)) g′(x)=g(x)(1−g(x))
具体请查看作者的另一篇文章《sigmoid函数及其图像绘制》
我们把之前的预测值进行sigmoid函数变换,则得到0~1的值,你可以把它看作是预测结果为True的概率。
比如,一张图片包含猫,则y=1,如果预测结果为0.9212,那么大概有92%的概率包含猫,18%的概率不包含猫(当然可能不是严格意义上的概率)。
在验证数据时,得到的预测结果是0~1的小数,我们可以假定大于0.5则为True,否则为False。
三、假设函数
引入sigmoid函数之后,假设函数就成了
h ( x ( i ) ) = g ( w x ( i ) ) = 1 1 + e − w x ( i ) \begin{aligned} h(x^{(i)})&=g(wx^{(i)})\\ &=\frac1{1+e^{-wx^{(i)}}} \end{aligned} h(x(i))=g(wx(i))=1+e−wx(i)1
四、代价函数
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义。但是问题在于,当我们将 h ( x ) h(x) h(x)代入到这样定义的代价函数中时,我们得到的代价函数将是一个非凸函数。这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
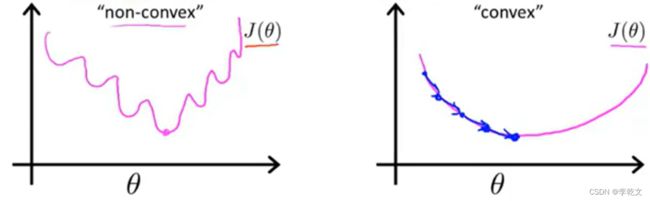
(PS:关于凸函数的证明在此不做讲解,读者有兴趣可以自行查找相关资料。此处贴一篇文章便于扩展思路《凸函数》)
所以,我们需要改变代价函数模型。
我们重新定义逻辑回归的代价函数为: J = 1 m ∑ i = 1 m C o s t ( h ( x ( i ) ) − y ( i ) ) J=\frac1{m}\sum_{i=1}^mCost(h(x^{(i)})-y^{(i)}) J=m1∑i=1mCost(h(x(i))−y(i)) ,其中
C o s t = { − ln ( h ( x ( i ) ) ) if y ( i ) = 1 − ln ( 1 − h ( x ( i ) ) ) if y ( i ) = 0 Cost= \begin{cases} -\ln(h(x^{(i)})) &\text{if } y^{(i)}=1 \\ -\ln(1-h(x^{(i)})) &\text{if } y^{(i)}=0 \end{cases} Cost={−ln(h(x(i)))−ln(1−h(x(i)))if y(i)=1if y(i)=0
由于没有平方求导,所以我们不用 1 2 m \frac1{2m} 2m1直接用 1 m \frac1{m} m1即可。
我们使用代码画出 h ( x ( i ) ) ℎ(x^{(i)}) h(x(i))与 ( h ( x ( i ) ) , ( i ) ) (ℎ(x^{(i)}), ^{(i)}) Cost(h(x(i)),y(i))之间的关系:
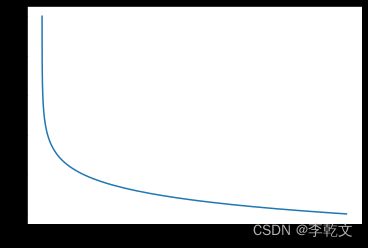
当 y ( i ) = 1 y^{(i)}=1 y(i)=1时, C o s t = − ln ( h ( x ( i ) ) ) Cost=-\ln(h(x^{(i)})) Cost=−ln(h(x(i))),代码及函数图像如下:
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-10, 10, 0.1) #起点,终点,间距
h = sigmoid(x)
#y=1时
Cost=-np.log(h) #以自然数e为底数
plt.plot(h, Cost)
plt.show()
如上图所示,在 y ( i ) = 1 y^{(i)}=1 y(i)=1的情况下:h=1时,误差Cost=0;h越小,误差越大;当h趋近于0时,误差趋近 + ∞ +\infty +∞,很好地反映了预测偏离的代价。
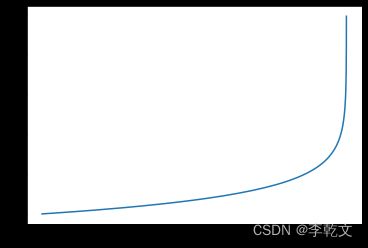
当 y ( i ) = 0 y^{(i)}=0 y(i)=0时: C o s t = − ln ( h ( x ( i ) ) ) Cost=-\ln(h(x^{(i)})) Cost=−ln(h(x(i)))
#y=0时
Cost=-np.log(1-h) #以自然数e为底数
plt.plot(h, Cost)
plt.show()
如上图所示,在 y ( i ) = 0 y^{(i)}=0 y(i)=0的情况下:h=0时,误差Cost=0;h越大,误差越大;当h趋近于1时,误差趋近 + ∞ +\infty +∞,也很好地反映了预测偏离的代价。
将构建的 C o s t ( h ( x ( i ) ) , y ( i ) ) Cost(h(x^{(i)}),y^{(i)}) Cost(h(x(i)),y(i))简化如下:
C o s t ( h ( x ( i ) ) , y ( i ) ) = − y ( i ) × ln ( h ( x ( i ) ) ) − ( 1 − y ( i ) ) × ln ( 1 − h ( x ( i ) ) ) Cost(ℎ(x^{(i)}),y^{(i)}) = -y^{(i)}×\ln(h(x^{(i)}))-(1-y^{(i)})×\ln(1-h(x^{(i)})) Cost(h(x(i)),y(i))=−y(i)×ln(h(x(i)))−(1−y(i))×ln(1−h(x(i)))
可以将 y ( i ) = 1 y^{(i)}=1 y(i)=1和 y ( i ) = 0 y^{(i)}=0 y(i)=0分别代入,即可得到之前的函数。
代入代价函数 J = 1 m ∑ i = 1 m C o s t ( h ( x ( i ) ) − y ( i ) ) J=\frac1{m}\sum_{i=1}^mCost(h(x^{(i)})-y^{(i)}) J=m1∑i=1mCost(h(x(i))−y(i))可得到:
J = 1 m ∑ i = 1 m [ − y ( i ) × ln ( h ( x ( i ) ) ) − ( 1 − y ( i ) ) × ln ( 1 − h ( x ( i ) ) ) ] = − 1 m ∑ i = 1 m [ y ( i ) × ln ( h ( x ( i ) ) ) + ( 1 − y ( i ) ) × ln ( 1 − h ( x ( i ) ) ) ] \begin{aligned} J&=\frac1{m}\sum_{i=1}^m[-y^{(i)}×\ln(h(x^{(i)}))-(1-y^{(i)})×\ln(1-h(x^{(i)}))]\\ &=-\frac1{m}\sum_{i=1}^m[y^{(i)}×\ln(h(x^{(i)}))+(1-y^{(i)})×\ln(1-h(x^{(i)}))]\\ \end{aligned} J=m1i=1∑m[−y(i)×ln(h(x(i)))−(1−y(i))×ln(1−h(x(i)))]=−m1i=1∑m[y(i)×ln(h(x(i)))+(1−y(i))×ln(1−h(x(i)))]
五、梯度下降
得到上述代价函数后,我们就可以跟线性回归一样,用梯度下降法来求出代价函数 J ( w ) J(w) J(w)最小时的 w w w参数了。
对 J ( w ) J(w) J(w)中的 w 0 , w 1 , … , w n w_0,w_1,\dots,w_n w0,w1,…,wn分别求偏导,求导相关知识可参考《导数与偏导》。
我们在这里对 w 0 , w 1 , … , w n w_0,w_1,\dots,w_n w0,w1,…,wn中的任意值 w i w_i wi,进行求导推理。
从上面可知,
J = − 1 m ∑ i = 1 m [ y ( i ) × ln ( h ( x ( i ) ) ) + ( 1 − y ( i ) ) × ln ( 1 − h ( x ( i ) ) ) ] J=-\frac1{m}\sum_{i=1}^m[y^{(i)}×\ln(h(x^{(i)}))+(1-y^{(i)})×\ln(1-h(x^{(i)}))] J=−m1i=1∑m[y(i)×ln(h(x(i)))+(1−y(i))×ln(1−h(x(i)))]
现在我们要进行链式求导,用到的求导公式有:
( ln ) ′ = 1 x (\ln{})^′ = \frac1x (lnx)′=x1
( k x ) ′ = k (kx)' = k (kx)′=k
( k ) ′ = 0 (k)'=0 (k)′=0
w x ( i ) = w 0 x 0 ( i ) + w 1 x 1 ( i ) + w 2 x 2 ( i ) + . . . + w n x n ( i ) wx^{(i)}=w_0x^{(i)}_0 + w_1x^{(i)}_1+w_2x^{(i)}_2+...+w_nx^{(i)}_n wx(i)=w0x0(i)+w1x1(i)+w2x2(i)+...+wnxn(i),我们把 w n w_n wn看作变量,其他的都看作常数,求导可得
∂ ∂ w n w x ( i ) = x n ( i ) \frac{∂}{∂w_n}wx^{(i)}=x^{(i)}_n ∂wn∂wx(i)=xn(i)
前面有提到simoid函数 g ( x ) = 1 1 + e − x g(x)=\frac1{1+e^{-x}} g(x)=1+e−x1,其导数为 g ′ ( x ) = g ( x ) ( 1 − g ( x ) ) g'(x)=g(x)(1-g(x)) g′(x)=g(x)(1−g(x))
有 h ( x ( i ) ) = g ( w x ( i ) ) h(x^{(i)})=g(wx^{(i)}) h(x(i))=g(wx(i))
那么:
∂ J ∂ w n = − 1 m ∑ i = 1 m [ y ( i ) 1 h ( x ( i ) ) ∂ h ( x ( i ) ) ∂ w n − ( 1 − y ( i ) ) 1 1 − h ( x ( i ) ) ∂ h ( x ( i ) ) ∂ w n ] = − 1 m ∑ i = 1 m [ y ( i ) 1 h ( x ( i ) ) − ( 1 − y ( i ) ) 1 1 − h ( x ( i ) ) ] ∂ h ( x ( i ) ) ∂ w n = − 1 m ∑ i = 1 m [ y ( i ) 1 g ( w x ( i ) ) − ( 1 − y ( i ) ) 1 1 − g ( w x ( i ) ) ] ∂ g ( w x ( i ) ) ∂ w n = − 1 m ∑ i = 1 m [ y ( i ) 1 g ( w x ( i ) ) − ( 1 − y ( i ) ) 1 1 − g ( w x ( i ) ) ] g ( w x ( i ) ) ( 1 − g ( w x ( i ) ) ) x n ( i ) = − 1 m ∑ i = 1 m [ y ( i ) ( 1 − g ( w x ( i ) ) ) − ( 1 − y ( i ) ) g ( w x ( i ) ) ] x n ( i ) = − 1 m ∑ i = 1 m [ y ( i ) − g ( w x ( i ) ) ] x n ( i ) = 1 m ∑ i = 1 m [ g ( w x ( i ) ) − y ( i ) ] x n ( i ) = 1 m ∑ i = 1 m [ h ( x ( i ) ) − y ( i ) ] x n ( i ) \begin{aligned} \frac{∂J}{∂w_n} &=-\frac1{m}\sum_{i=1}^m[y^{(i)}\frac1{h(x^{(i)})}\frac{∂h(x^{(i)})}{∂w_n}-(1-y^{(i)})\frac1{1-h(x^{(i)})}\frac{∂h(x^{(i)})}{∂w_n}] \\ &=-\frac1{m}\sum_{i=1}^m[y^{(i)}\frac1{h(x^{(i)})}-(1-y^{(i)})\frac1{1-h(x^{(i)})}]\frac{∂h(x^{(i)})}{∂w_n} \\ &=-\frac1{m}\sum_{i=1}^m[y^{(i)}\frac1{g(wx^{(i)})}-(1-y^{(i)})\frac1{1-g(wx^{(i)})}]\frac{∂g(wx^{(i)})}{∂w_n} \\ &=-\frac1{m}\sum_{i=1}^m[y^{(i)}\frac1{g(wx^{(i)})}-(1-y^{(i)})\frac1{1-g(wx^{(i)})}]g(wx^{(i)})(1-g(wx^{(i)})) x^{(i)}_n\\ &=-\frac1{m}\sum_{i=1}^m[y^{(i)}(1-g(wx^{(i)}))-(1-y^{(i)})g(wx^{(i)})] x^{(i)}_n\\ &=-\frac1{m}\sum_{i=1}^m[y^{(i)}-g(wx^{(i)})] x^{(i)}_n\\ &=\frac1{m}\sum_{i=1}^m[g(wx^{(i)})-y^{(i)}] x^{(i)}_n\\ &=\frac1{m}\sum_{i=1}^m[h(x^{(i)})-y^{(i)}] x^{(i)}_n\\ \end{aligned} ∂wn∂J=−m1i=1∑m[y(i)h(x(i))1∂wn∂h(x(i))−(1−y(i))1−h(x(i))1∂wn∂h(x(i))]=−m1i=1∑m[y(i)h(x(i))1−(1−y(i))1−h(x(i))1]∂wn∂h(x(i))=−m1i=1∑m[y(i)g(wx(i))1−(1−y(i))1−g(wx(i))1]∂wn∂g(wx(i))=−m1i=1∑m[y(i)g(wx(i))1−(1−y(i))1−g(wx(i))1]g(wx(i))(1−g(wx(i)))xn(i)=−m1i=1∑m[y(i)(1−g(wx(i)))−(1−y(i))g(wx(i))]xn(i)=−m1i=1∑m[y(i)−g(wx(i))]xn(i)=m1i=1∑m[g(wx(i))−y(i)]xn(i)=m1i=1∑m[h(x(i))−y(i)]xn(i)
公式推导参考文章《逻辑回归的梯度下降公式详细推导过程》
重复以下计算:
w n = w i − η ∗ ∂ ∂ w n J ( w ) = w n − η ∗ 1 m ∑ i = 1 m [ g ( w x ( i ) ) − y ( i ) ] x n ( i ) \begin{aligned} w_n &= w_i-η*\frac{∂}{∂w_n}J(w)\\ &=w_n-η*\frac1{m}\sum_{i=1}^m[g(wx^{(i)})-y^{(i)}] x^{(i)}_n \end{aligned} wn=wi−η∗∂wn∂J(w)=wn−η∗m1i=1∑m[g(wx(i))−y(i)]xn(i)
η η η称之为学习率,控制梯度下降时每一段走的距离。
一直迭代计算,直到 w 0 , w 1 , … , w n w_0,w_1,\dots,w_n w0,w1,…,wn变化很小为止,代表已经达到最小值或者局部最小值了,此时 w w w确定下来。
最终批量梯度下降的矩阵运算写法是 w = w − η m ( w x − y ) x T w=w-\fracη{m}(wx-y)x^T w=w−mη(wx−y)xT
矩阵运算推导过程参考《机器学习 多变量线性回归》梯度下降章节。
六、二分类原生代码实现
6.1 生成模拟数据
具体可以参考另一篇文章《sklearn 使用make_classification生成分类样本数据》
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
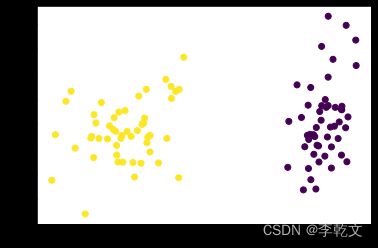
X, Y = make_classification(n_samples=100,n_features=2,n_informative=2,n_clusters_per_class=1,n_classes=2,n_redundant=0,random_state=1)
XT=X.T
plt.scatter(
XT[0], #x坐标
XT[1], #y坐标
c=Y
)
plt.show()
print(X.shape,Y.shape)
print(X)
print(Y)
(100, 2) (100,)
[[-1.04948638 0.8786438 ]
[ 0.8780991 0.89551051]
[ 0.95928819 1.03967316]
[-1.18013412 1.12062155]
[-0.90731836 1.06040861]
[-0.62754626 1.37661405]
[ 0.82178321 1.18947778]
[-1.20376927 0.78801845]
[ 0.77151441 0.345716 ]
[-0.493857 1.66752297]
[ 1.17456965 0.69211449]
[ 0.82798737 0.84806927]
[ 0.89189141 0.87699465]
[ 0.90394545 0.35413361]
[ 0.94459507 1.12641981]
[ 0.9317172 0.78344054]
[-0.96853969 1.27991386]
[-1.09230828 0.92686981]
[-0.68243019 1.4468218 ]
[-0.76045809 0.61363671]
[-1.1146902 1.13545112]
[ 1.32970299 1.58463774]
[-1.39003042 0.85771953]
[ 1.01313574 1.16777676]
...
[-0.54245992 1.34740825]]
[1 0 0 1 1 1 0 1 0 1 0 0 0 0 0 0 1 1 1 1 1 0 1 0 0 1 0 0 0 1 1 1 1 0 0 1 0
0 0 0 1 1 0 0 1 0 1 1 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 0 0 1 0 0 0 1 0 0 0 1
1 1 0 1 1 1 0 0 0 1 1 1 0 1 1 1 0 1 0 0 1 0 1 1 0 1]
6.2 添加前置与数据分割
添加x0=1的前置,然后将数据分割成训练数据与验证数据。
import numpy as np
np.set_printoptions(suppress=True) #numpy不使用科学计数法
from sklearn.model_selection import train_test_split
#添加前置 x0=1
temp = np.ones([X.shape[0],X.shape[1]+1])
temp[:,1:] = X #第[0]行到最后一行的(第[1]列到最后一列)赋值为X
X = temp
# 将数据分割为训练和验证数据,都有特征和预测目标值
# 分割基于随机数生成器。为random_state参数提供一个数值可以保证每次得到相同的分割
train_X, val_X, train_y, val_y = train_test_split(X, Y, random_state = 0)
print(train_X.shape, val_X.shape, train_y.shape, val_y.shape)
(75, 3) (25, 3) (75,) (25,)
6.3 迭代训练
#损失函数
def loss(preY,trainY):
return -1/m*(trainY*np.log(preY)+(1-trainY)*np.log(1-preY)).sum()
def sigmoid(x):
return 1/(1+np.exp(-x))
learn_rate=0.5 #学习率
m=train_X.shape[0]
n=train_X.shape[1] #由于添加了前置,这里的n等于文章中的n+1
w=np.zeros([1,n]) #初始化参数w,1行n列
# train_y=train_y.reshape([1,m])
count=0 #迭代次数
plt_epoch=[]
plt_loss=[]
#迭代
for i in range(10000):
preY=sigmoid(w.dot(train_X.T)) #预测值,1行m列,由于数据集是m行n列,这里的train_X.T就是文章中的x
w_C=(learn_rate/m)*(preY-train_y).dot(train_X)
if count%100==0:
#每迭代100次则输出误差值
ls=loss(preY,train_y)
print('epoch:',count,'loss:',ls)
plt_epoch.append(count)
plt_loss.append(ls)
#若w变化不大,则暂停迭代,模型训练完成
if (np.abs(w_C)<0.001).all():
print('最终w变化量:',w_C)
break
count+=1
w-=w_C
print('迭代次数:',count)
print('w权重:',w)
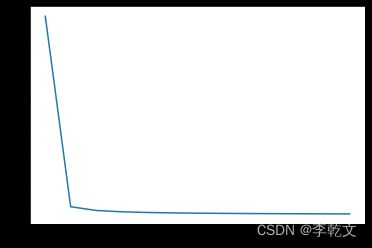
#绘制迭代次数与损失函数的关系
plt.plot(plt_epoch,plt_loss)
epoch: 0 loss: 0.6931471805599454
epoch: 100 loss: 0.02806346493668348
epoch: 200 loss: 0.01497424185854577
epoch: 300 loss: 0.010341734055737531
epoch: 400 loss: 0.007945436620121295
epoch: 500 loss: 0.006473035961682875
epoch: 600 loss: 0.005473323387074791
epoch: 700 loss: 0.0047485829736239145
epoch: 800 loss: 0.004198225319392855
epoch: 900 loss: 0.0037655642147051117
epoch: 1000 loss: 0.003416173435881908
epoch: 1100 loss: 0.0031279137308657568
epoch: 1200 loss: 0.002885887831874862
最终w变化量: [[ 0.00000628 0.00099987 -0.00010276]]
迭代次数: 1262
w权重: [[ 0.09543459 -6.92496003 0.34671816]]
6.4 验证数据
preY=np.where(sigmoid(w.dot(val_X.T))>0.5,1,0) #由于数据集是m行n列,这里的val_X.T就是文章中的x
print('预测:',preY)
print('实际:',val_y)
print('误差:',preY-val_y)
预测: [[0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 1 1 0 0]]
实际: [0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 1 1 0 0]
误差: [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
七、sklearn代码实现
from sklearn.linear_model import LogisticRegression
import joblib
#初始化模型
lr_model = LogisticRegression()
#训练
lr_model.fit(train_X, train_y)
#保持模型
joblib.dump(lr_model, './LogisticRegression_Binary.model')
#加载模型,在实际应用中直接加载已训练好的模型
lr_model = joblib.load('./LogisticRegression_Binary.model')
#预测
y_pred = lr_model.predict(val_X)
print("Prediction on test set:", y_pred)
print("Score on test set:", lr_model.score(val_X, val_y))
运行结果
Prediction on test set: [0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 0 0 0 1 1 0 0]
Score on test set: 1.0