极限多标签算法: FastXML 的解析
文章目录
- 前言
- 1.关于极限多标签 (XML: eXtreme multi-label Classification)
-
- 1.1 流派
- 1.2 评价指标
- 2.FastXML
-
- 2.1 FastXML的特点
- 2.2 FastXML的局部性
- 2.3 FastXML的拟合目标
- 2.4 通过代码分析FastXML的拟合细节
-
- 2.4.1 r ± \mathbf{r}^{±} r±的优化与拟合
- 2.4.2 δ \delta δ的优化与拟合 ---- 正负区划分的核心
- 2.4.3 w \mathbf{w} w的优化与拟合
- 2.5 树的训练
-
- 2.5.1 主体
- 2.5.2 `shrink_data_matrices`函数 (注释1)
- 2.5.3 `calc_leaf_prob`函数 (注释2)
- 2.5.4 `postprocess_node`函数 (注释3)
- 2.6 基于训练完毕的树模型来进行数据预测
-
- 2.6.1 预测数据在单个树中的决策
- 2.6.2 多个树预测的集成
- 3.FastXML的总结与思考
前言
摘要: 本次分享的文章来自:
Yashoteja Prabhu and Manik Varma, FastXML: A Fast, Accurate and Stable Tree-classifier for eXtreme Multi-label Learning.
论文PDF下载: http://manikvarma.org/pubs/prabhu14.pdf
代码: http://manikvarma.org/code/FastXML/download.html
本来挺早就看了这篇文章, 但是代码是这几周陆续看的, 感觉有点难度.
原作者写FastXML这个算法是用C++写的, 然后用matlab套上了运行器以及一些评价指标的接口.
虽然我本科是学过C++, 但是也挺久没有用过了, 这次稍微重温了一些东西, 以便能看到一些代码中的细节.
1.关于极限多标签 (XML: eXtreme multi-label Classification)
极限多标签是多标签的超级加强版本
- 更多的数据量, 百万的量级. 而且这个量级不仅仅是数据矩阵, 还有标签矩阵
- 极强的数据稀疏性, 数据矩阵中大量的零元素占比. 有些多标签算法在数据稀疏的矩阵中的表现是显著糟糕的 (
啊没错, 是我自己做的算法). - 极强的标签稀疏性, 标签矩阵中的大量零占比. 虽然目前感觉很多算法对于多标签问题的这个方向有优化, 但是若这个稀疏度夸张到一定程度还是非常难搞的.
- 严重的缺值: 很多的标签是没有标记的, 有可能一个实例对应的几百万的标签中只有寥寥10个被标记了
这样的问题直接导致的结果就是面对XML, 常规的多标签学习方案几乎全部不能用了, 因为时间开销太大了.
这里介绍了一些经典的XML算法, 同时也列出了它们的时间开销比对, 以及给了些经典极限数据的下载http://manikvarma.org/downloads/XC/XMLRepository.html
1.1 流派
从论文的引言和之前导师的辅导中简单了解到了一些流派
- 1-vs-All: 给每个标签单独建立分类器, 有很高的复杂度, 基本上是 标签数 × \times ×实例数 × \times ×正标签数目 这样的量级.
- 层次(Hierarchy)结构: 其实就是一种树形结构, 它借助了有关树的数据结构来削减线性的查找开销. FastXML正是这种思路.
- Embeddings 嵌入: 这是一种很自然的思路, 既然我们的数据大多处于高维且低轶, 那我们就通过一些矩阵的手段来对数据进行降维. 通过 D × D ′ D\times D^{\prime} D×D′的矩阵来提取特征数, 通过 L × L ′ L\times L^{\prime} L×L′的矩阵来提取标签数.
1.2 评价指标
其实在常规的多标签问题中有的算法会试着用Accuracy的评价指标, 但是严格来说这样的评价指标对于多标签是不准确的.
多标签还是更喜欢基于排序的评价指标, 我们往往喜欢用 F 1 F_1 F1 (最好通过Peak- F 1 F_1 F1的手段), AUC, NDCG等.
此外, 这些评价指标也可以作为算法拟合的思路.
例如, FastXML就提出了基于 NDCG 的排名损失函数来实现显着更高的准确度.
NDCG有个很好的性质, 因为是基于排序的, 往往我们只需要关心前 k k k个数据的排序情况往往就能近似表示全局, 这就是NDCG@k.
虽然其他基于排序的评价指标也能采用这种思路, 但是他们的计算有一定的困难, 可能需要全局的一些参数, 但是NDCG就很亲民.
因此对于XML问题, 我们尽可能选择1.简单 2.高效(减少计算体量)的评价指标.
DCG的定义公式:
L D C G ( r , y ) = ∑ l = 1 k y r l log ( 1 + l ) (1) \mathcal{L}_{\mathrm{DCG}}(\mathbf{r}, \mathbf{y})=\sum_{l=1}^{k} \frac{y_{r_{l}}}{\log (1+l)} \tag{1} LDCG(r,y)=l=1∑klog(1+l)yrl(1)
这里的 r \mathbf{r} r代表一种排列顺序,这么说可能略抽象.
我令 Π ( 1 , L ) \Pi(1, L) Π(1,L)表示 { 1 , 2 , … , L } \{1,2,\dots,L\} {1,2,…,L}的所有可能的组合构成的集合, 那么 r ∈ Π ( 1 , L ) \mathbf{r} \in \Pi(1, L) r∈Π(1,L)
而 L D C G ( r , y ) \mathcal{L}_{\mathrm{DCG}}(\mathbf{r},\mathbf{y}) LDCG(r,y)就是对于某个向量 y \mathbf{y} y, 将其原序列按照 r \mathbf{r} r排序方式重排后, 计算其DCG的函数. y r l y_{r_l} yrl表示 r \mathbf{r} r序中第 l l l个元素的向量值 (这里的向量值就是0/1, 因为向量 y \mathbf{y} y其实是标签向量).
在DCG的基础上进行归一化, 于是提出了NDCG
L n D C G @ k ( r , y ) = I k ( y ) ∑ l = 1 k y r l log ( 1 + l ) where I k ( y ) = 1 ∑ l = 1 min ( k , 1 ⊤ y ) 1 log ( 1 + l ) (2) \begin{aligned} \mathcal{L}_{\mathrm{nDCG} @ k}(\mathbf{r}, \mathbf{y}) &=I_{k}(\mathbf{y}) \sum_{l=1}^{k} \frac{y_{r_{l}}}{\log (1+l)} \\ \text { where } I_{k}(\mathbf{y}) &=\frac{1}{\sum_{l=1}^{\min \left(k, \mathbf{1}^{\top} \mathbf{y}\right)} \frac{1}{\log (1+l)}} \end{aligned} \tag{2} LnDCG@k(r,y) where Ik(y)=Ik(y)l=1∑klog(1+l)yrl=∑l=1min(k,1⊤y)log(1+l)11(2)
本质上NDCG是DCG除IDCG得到的, 上式将IDCG以倒数的形式 I k ( y ) I_{k}(\mathbf{y}) Ik(y)体现了出来.
IDCG可以认为是最好的DCG, 因此这里默认都将 y r l y_{r_l} yrl设置为1.
min ( k , 1 ⊤ y ) {\min \left(k, \mathbf{1}^{\top} \mathbf{y}\right)} min(k,1⊤y)其实就是挑选 y \mathbf{y} y向量的前 k k k个, 若 k k k大于向量本身就选向量的长度.
其实可以发现, 我们只要提供向量 y \mathbf{y} y的长度和 k k k, 那么 I k ( y ) I_{k}(\mathbf{y}) Ik(y)就能确定下来, 他和 r \mathbf{r} r与具体 y \mathbf{y} y中某个 y r l y_{r_l} yrl是无关的. 因此在编程中若提前确定了 y \mathbf{y} y的长度和 k k k, 那么 I k ( y ) I_{k}(\mathbf{y}) Ik(y)是能提前算出来的.
2.FastXML
2.1 FastXML的特点
FastXML借鉴了多标签随机森林(MLRF)算法 和 次线性排名的标签 (LPSR) 划分算法
R. Agrawal, A. Gupta, Y. Prabhu, and M. Varma. Multi-label learning with millions of labels: Recommending advertiser bid phrases for web pages. In WWW, pages 13–24, 2013.
J. Weston, A. Makadia, and H. Yee. Label partitioning for sublinear ranking. In ICML, volume 28, pages 181–189, 2013.
MLRF (随机森林)主要提供了FastXML整体学习的一个框架和流程, LPSR主要体现在后续为每个结点进行正负划分提供一种思路. (LPSR后续可能会再去学习一下)
采用LPSR的MLRF既消除了MLRF算法中任务无关的基尼指数(Gini index), 也缓解了LPSR导致的聚类误差. 进一步, FastXML 相比于单独的MLRF, 在划分时的效率要明显高于Gini和信息增益, 相比于单独的LPSR, 无需首先学习量大的基分类器才保证得了准确预测.
(↑这是原论文赞扬自己的文字, 验证这个问题还需要更深一步理解LPSR才能进一步展开说)
之前XML的层次结构可能会有较好的表现, 但是在许多应用程序中是不可用的. 于是原作者提出FastXML总之可作用多领域的XML层次模型.
总结作者的想法 (FastXML的贡献):
- FastXML提出了一个简单轻巧的Node partition方法
- 直接基于评价指标NDCG进行优化
- 将一系列花里胡哨的东西总结在树形结构上, 并得到及其优秀的速度
2.2 FastXML的局部性
XML几乎没法对全局测量, 因此大多数XML算法几乎都局部的, FastXML也是如此. 优化全局的测量可能是昂贵的, 因为树中进行全局测量需要对所有结点进行联合学习. MLRF和LPSR都有对这方面进行局部性进行优化的想法, 但是很遗憾, 他们都无法作用在XML和基于排名的策略中.
也就是说, MLRF和LPSR本身就具有良好的可用预测大量不相关标签的能力.
2.3 FastXML的拟合目标
FastXML的目标是构造一个最佳的随机森林, 其中每颗树都是对于整体数据集的一次有效的训练, 只不过初始分配的随机子是不同的.
- 训练时, 每次划分的依据都是当前结点的实例集 n . I D n.ID n.ID对应的标签向量的正/负情况, 正的将变为后续的左子树, 负的转变为右子树. 而确定哪些标签属于正区, 哪些标签属于负区, 这个就是我们拟合需要做的事情第一件事情, 即在训练时拟合出一个合理的树结构;
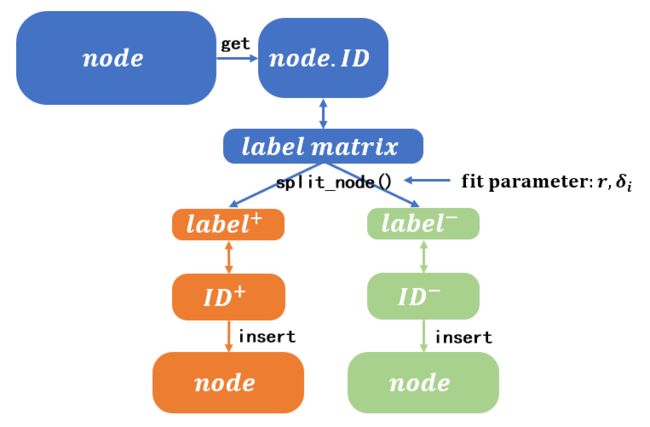
- 在树确定时, 我们进行预测时, 是按照每个结点独立的 w \mathbf{w} w向量与当前进入这个结点的测试数据做向量积, 通过结果的正负性来判断测试数据应当划入哪个 n . I D n.ID n.ID的分区.
当然, 这里的 “独立的 w \mathbf{w} w向量” 也需要在训练中确定, 这个就是我们拟合需要做的事情第二件事情, 即拟合 w \mathbf{w} w向量;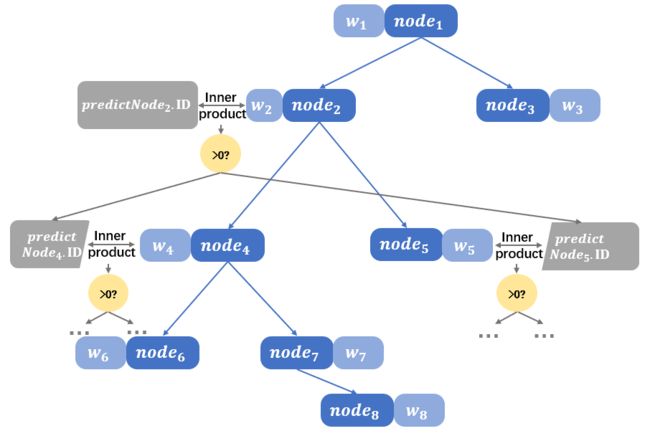
拟合的参数有三: w \mathbf{w} w, δ i \delta_i δi, r \mathbf{r} r. 三者都在训练时完成拟合, 但是测试预测时只会用到第一个参数. 于是作者提出了下面这样的拟合目标:
min ∥ w ∥ 1 + ∑ i C δ ( δ i ) log ( 1 + e − δ i w ⊤ x i ) − C r ∑ i 1 2 ( 1 + δ i ) L n D C G @ L ( r + , y i ) − C r ∑ i 1 2 ( 1 − δ i ) L n D C G @ L ( r − , y i ) w.r.t. w ∈ R D , δ ∈ { − 1 , + 1 } L , r + , r − ∈ Π ( 1 , L ) (3) \begin{aligned} \min &\|\mathbf{w}\|_{1}+\sum_{i} C_{\delta}\left(\delta_{i}\right) \log \left(1+e^{-\delta_{i} \mathbf{w}^{\top} \mathbf{x}_{i}}\right) \\ &-C_{r} \sum_{i} \frac{1}{2}\left(1+\delta_{i}\right) \mathcal{L}_{\mathrm{nDCG} @L}\left(\mathbf{r}^{+}, \mathbf{y}_{i}\right) \\ &-C_{r} \sum_{i} \frac{1}{2}\left(1-\delta_{i}\right) \mathcal{L}_{\mathrm{nDCG}@L}\left(\mathbf{r}^{-}, \mathbf{y}_{i}\right) \\ \text { w.r.t. } & \mathbf{w} \in \mathcal{R}^{D}, \boldsymbol{\delta} \in\{-1,+1\}^{L}, \mathbf{r}^{+}, \mathbf{r}^{-} \in \Pi(1, L) \end{aligned}\tag{3} min w.r.t. ∥w∥1+i∑Cδ(δi)log(1+e−δiw⊤xi)−Cri∑21(1+δi)LnDCG@L(r+,yi)−Cri∑21(1−δi)LnDCG@L(r−,yi)w∈RD,δ∈{−1,+1}L,r+,r−∈Π(1,L)(3)
上式的 i i i均表示针对结点 i i i的讨论. 有关的 C C C都是调节各项重要性的参数, 由用户敲定.
-
∥ w ∥ 1 \|\mathbf{w}\|_1 ∥w∥1是权值向量 w \mathbf{w} w的一范数, 这里我们显然希望权值向量 w \mathbf{w} w线性分割器足够稀疏, 每个结点涉及的属性越少越好, 确保权值向量尽可能提取当前实例组中共同的更具代表性的特征.
w \mathbf{w} w的拟合过程中与其他两个参数的交集比较少, 这个问题在于 w \mathbf{w} w的拟合相比于 δ i \delta_i δi和 r \mathbf{r} r会更独立且困难. -
第二项里面包含了一个 w \mathbf{w} w和 δ i \delta_i δi, δ i \delta_i δi仅可能为+1/-1, 它表示在训练时我们为这个结点判定的分区 (正? or 负区?), 而 w ⊤ x i \mathbf{w}^{\top} \mathbf{x}_{i} w⊤xi表示用训练集的数据进行测试时, 当前结点的实例组 n . I D n.ID n.ID与 w \mathbf{w} w做内积时判定的分区 (正? or 负区?).
显而易见, 当测试与训练一致了我们的模型就是有效的, 因此 δ i \delta_i δi与 w ⊤ x i \mathbf{w}^{\top} \mathbf{x}_{i} w⊤xi同号时, log ( 1 + e − δ i w ⊤ x i ) \log \left(1+e^{-\delta_{i} \mathbf{w}^{\top} \mathbf{x}_{i}}\right) log(1+e−δiw⊤xi)最小.
w \mathbf{w} w的拟合方法是newGLMNET算法
G.-X. Yuan, C.-H. Ho, and C.-J. Lin. An improved glmnet for l1-regularized logistic regression. JMLR, 13:1999–2030, 2012.
- 第三项和第四项是互斥的两个项, 他们共同参与了 δ i \delta_i δi与 r \mathbf{r} r的拟合, δ i = + 1 \delta_i=+1 δi=+1时第一项的拟合是有效的, 而第二项无效, 反之亦然. 而 r \mathbf{r} r主要依靠NDCG拟合, 我们会保证当前结点的标签组在最好的分区安排下获得最适合的值NDCG.
2.4 通过代码分析FastXML的拟合细节
2.4.1 r ± \mathbf{r}^{±} r±的优化与拟合
式3中关于 r ± \mathbf{r}^{±} r±的公式因为两项之间的互斥性, 因此可以简单表示为:
max r ± ∈ Π ( 1 , L ) ∑ i : δ i = ± 1 I L ( y i ) ∑ l = 1 L y i r l ± log ( 1 + l ) (4) \max _{\mathbf{r} \pm \in \Pi(1, L)} \sum_{i: \delta_{i}=\pm 1} I_{L}\left(\mathbf{y}_{i}\right) \sum_{l=1}^{L} \frac{y_{i r_{l}^{\pm}}}{\log (1+l)}\tag{4} r±∈Π(1,L)maxi:δi=±1∑IL(yi)l=1∑Llog(1+l)yirl±(4)
在原论文中, 将4式最终转化为一种易编程的表达 (具体推导详情可见原论文中的7~11式):
r ± ∗ = rank L ( ∑ i : δ i = ± 1 I L ( y i ) y i ) (5) \mathbf{r}^{\pm^{*}}=\operatorname{rank}_{L}\left(\sum_{i: \delta_{i}=\pm 1} I_{L}\left(\mathbf{y}_{i}\right) \mathbf{y}_{i}\right)\tag{5} r±∗=rankL(i:δi=±1∑IL(yi)yi)(5)
在这里的 rank L \operatorname{rank}_{L} rankL在原文中有定义, 他的作用就是让其解释的向量按照值从大到小的顺序重排, 并最终返回重排后的下标. 例如[1,8,5,10]的下标是[0,1,2,3], 重排后原数组是[10,8,5,1], 返回的 rank L \operatorname{rank}_{L} rankL就是[3,1,2,0].
式5展示的 rank L \operatorname{rank}_{L} rankL内部内容是计算出每个标签在自己所在的正负区内求 I L ( y i ) y i I_{L}\left(\mathbf{y}_{i}\right) \mathbf{y}_{i} IL(yi)yi之和, 最终所有正区标签之和的 rank L \operatorname{rank}_{L} rankL值返回给 r + \mathbf{r}^+ r+, 负区的给 r − \mathbf{r}^- r−.
为何这样的 r \mathbf{r} r是最优的, 因为它的拟合依据本身就是NDCG, 若权值越高的数也拥有更高的排名, 那么NDCG自然就会很高. 而确定每个权值最合适的位置, 最显然是按照贪心的想法, 只要将权值从高到小排序即可.
下面给出源码中对于这部分的解释:
VecF idcgs( num_X ); // num_X表示标签个数
for( _int i=0; i<num_X; i++ )
idcgs[i] = 1.0/csum_discounts[ size[i] ];
// 计算每个标签的I_{L}(y_i). size[i]表示第i个标签拥有的非零元个数
VecIF pos_sum( num_Y ); // num_Y表示一个标签的维数
VecIF neg_sum( num_Y );
...
while(true)
{
for(_int i=0; i<num_Y; i++ ) // 初始化pos_sum, neg_sum
{
pos_sum[i] = make_pair(i,0); // 正区所有标签的和
neg_sum[i] = make_pair(i,0); // 负区所有标签的和
...
}
for( _int i=0; i<num_X; i++ ) // 遍历每个标签 (num_X是标签数)
{
for( _int j=0; j<size[i]; j++ ) // 遍历每个标签的特征 (size[i]表示第i个标签实际具有的非0元个数)
{
_int lbl = data[i][j].first;// 取得当前特征实际的下标(于实际邻接矩阵中)
_float val = data[i][j].second * idcgs[i];
// 计算I_{L}(y_i)y_i
if(pos_or_neg[i]==+1)
pos_sum[lbl].second += val;
else
neg_sum[lbl].second += val;
}
}
new_ndcg = 0;
// s \in {-1, +1}
for(_int s=-1; s<=1; s+=2) // 选定分区, 确定一个δ_i
{
VecIF& sum = s==-1 ? neg_sum : pos_sum;
// sort按值排序这个过程就是贯彻论文中的rank_L
// 对一个标签内部排序的前num_Y(也就是L)个信息排序
sort(sum.begin(), sum.begin()+num_Y, comp_pair_by_second_desc<_int,_float>);
...
}
}
}
这里 r \mathbf{r} r结果就蕴含在的sum的first成员之中 (序号的排序).
另外, 这里idcgs[i]表示着第i个标签的 I L ( y i ) I_L(y_i) IL(yi)值, 它是由表示 I D C G IDCG IDCG的csum_discounts计算得到的. 它表示第 i i i个标签的 I L ( y i ) I_L(y_i) IL(yi)值.
一个标签的 I D C G @ L IDCG@L IDCG@L计算过程非常简单, 实践上一个只由0/1构成的长度为 L L L标签向量的 I D C G IDCG IDCG值仅仅由这 L L L个数据的前若干个非零值有关系.
因此在读入标签矩阵后, 那么每个标签的 I D C G IDCG IDCG其实是可以计算出来的.
下面是csum_discounts变量的全局预计算
csum_discounts[0] = 1.0;
_float sumd = 0;
for( _int i=0; i<num_Y; i++ )
{
discounts[i] = 1.0/log2((_float)(i+2));
sumd += discounts[i];
if(USE_IDCG)
csum_discounts[i+1] = sumd;
else
csum_discounts[i+1] = 1.0; // 可见, 若我们单纯只用DCG的话iDCG是全1
}
事先确定了这个存储后, 后续如果我们在计算标签的IDCG时, 若这个标签中有 k k k个非零项, 那么可以直接用csum_discounts[k] 代表这个标签的 I D C G IDCG IDCG.
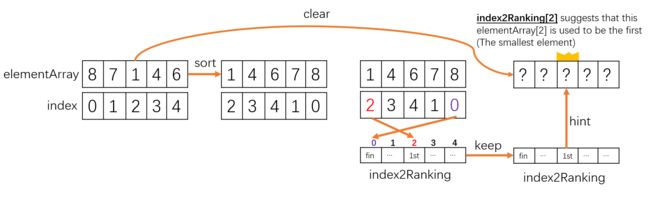
上述内容可以用一张图来描述:
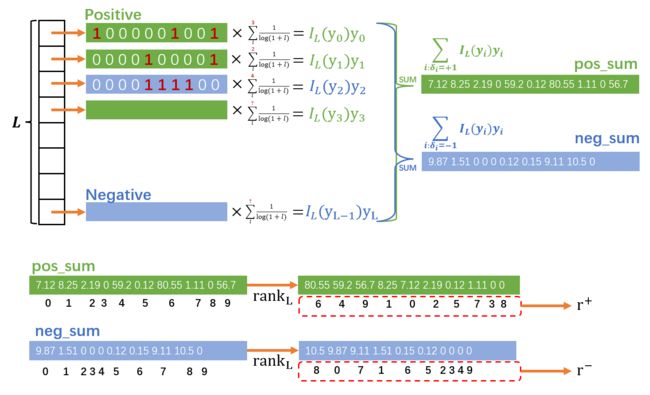
这里绿色表示正区的标签, 每个标签乘上自己的 I L ( y i ) I_L(y_i) IL(yi), 然后求和得单个正区求和矩阵, 这个矩阵通过排名并保留排序后的原下标为 r + \mathbf{r}^+ r+. 蓝色的负区标签处理思路是类似的.
这个图我将标签维度缩小了, 实际上我们处理的数据的维度是非常大且稠密的
2.4.2 δ \delta δ的优化与拟合 ---- 正负区划分的核心
论文中将3式进一步化简得到了下面的式子:
v i ± = C δ ( ± 1 ) log ( 1 + e ∓ w ⊤ x i ) − C r I L ( y i ) ∑ l = 1 L y i r l ± log ( 1 + l ) (6) v_{i}^{\pm}=C_{\delta}(\pm 1) \log \left(1+e^{\mp \mathbf{w}^{\top} \mathbf{x}_{i}}\right)-C_{r} I_{L}\left(\mathbf{y}_{i}\right) \sum_{l=1}^{L} \frac{y_{i r_{l}^{\pm}}}{\log (1+l)}\tag{6} vi±=Cδ(±1)log(1+e∓w⊤xi)−CrIL(yi)l=1∑Llog(1+l)yirl±(6)
- 这个式子是将 w \mathbf{w} w固定住, 因此原3式中的第一项被删了.
- 然后选取最好的 r \mathbf{r} r, 也就是固定住 r \mathbf{r} r (正区的家伙就选择最好的 r + \mathbf{r}^{+} r+, 负区就选择最好的 r − \mathbf{r}^{-} r−)
- 之前3式的第2项是对于标签中的每个特征的对数运算求和 ( ∑ i C δ ( δ i ) log ( 1 + e − δ i w ⊤ x i ) \sum_{i} C_{\delta}\left(\delta_{i}\right) \log \left(1+e^{-\delta_{i} \mathbf{w}^{\top} \mathbf{x}_{i}}\right) ∑iCδ(δi)log(1+e−δiw⊤xi)), 然后拟合最小. 但是作者认为, 实际上我们的 δ \delta δ是对于标签向量的每个特征分配的一种参数, 因此其实只要保证每个特征都能得到最好的 δ i \delta_i δi, 那么全局一定是最优的, 于是在这个新的6式中并没有对这项求和.
- 6式中的第二项其实就是3式中最后两项的混合, 并且带入了 L n D C G @ L ( r ± , y i ) \mathcal{L}_{\mathrm{nDCG}@L}\left(\mathbf{r}^{±}, \mathbf{y}_{i}\right) LnDCG@L(r±,yi)来的展开结果.
- v i + v_i^+ vi+和 v i − v_i^- vi−可以认为是在 δ i \delta_i δi取+1或者-1的情况下得到的一种对当前标签的正负选择最优性的量化评价, 越低证明效果越好 (越低损失越小).
故在 v i − < v i + v_i^- < v_i^+ vi−<vi+的时候, δ i = − 1 \delta_i = -1 δi=−1是最优的, 反之亦然, 故得到了标签 i i i的拟合目标: δ i ∗ = sign ( v i − − v i + ) (7) \delta_{i}^{*}=\operatorname{sign}\left(v_{i}^{-}-v_{i}^{+}\right)\tag{7} δi∗=sign(vi−−vi+)(7)
然后就是我自己的想法了…我试着将 v v v带进去, 然后得到了下面的8式: δ i ∗ = sign ( C r I L ( y i ) ∑ l = 1 L − y i r l − + y i r l + log ( 1 + l ) − 2 C δ [ log ( 1 + e w ⊤ x i ) + log ( 1 + e − w ⊤ x i ) ] ) (8) \delta_i^{*}= \text{sign} \left( C_{r} I_{L}\left(\mathbf{y}_{i}\right) \sum_{l=1}^{L} \frac{-y_{i r_{l}^{-}}+y_{i r_{l}^{+}}}{\log (1+l)}-2C_{\delta} [\log \left(1+e^{\mathbf{w}^{\top} \mathbf{x}_{i}}\right)+\log \left(1+e^{-\mathbf{w}^{\top} \mathbf{x}_{i}}\right)] \right) \tag{8} δi∗=sign(CrIL(yi)l=1∑Llog(1+l)−yirl−+yirl+−2Cδ[log(1+ew⊤xi)+log(1+e−w⊤xi)])(8)
然后在代码部分中似乎它只关注了前半部分?
下面代码中的内容是在拟合 r \mathbf{r} r的基础上添加的, 因为拟合 δ \delta δ的基础就是在固定最优的 r \mathbf{r} r为基础.
_bool optimize_ndcg( SMatF* X_Y, VecI& pos_or_neg ) // X_Y是带有压缩信息cdata的压缩矩阵, pos_or_neg是实例的正负分割信息, +1/-1
{
_int num_X = X_Y->nc; // 标签个数
_int num_Y = X_Y->nr; // 一个标签的维度
_int* size = X_Y->size; // 每个标签拥有的正标签个数
pairIF** data = X_Y->data; // 存储的地址
_float eps = 1e-6;
VecF idcgs( num_X );
for( _int i=0; i<num_X; i++ )
idcgs[i] = 1.0/csum_discounts[ size[i] ];
VecIF pos_sum( num_Y );
VecIF neg_sum( num_Y );
VecF diff_vec( num_Y );
_float ndcg = -2;
_float new_ndcg = -1;
while(true)
{
for(_int i=0; i<num_Y; i++ ) // 初始化pos_sum, neg_sum, diff_vec
{
pos_sum[i] = make_pair(i,0); // 正区所有标签的和
neg_sum[i] = make_pair(i,0); // 负区所有标签的和
diff_vec[i] = 0; // 初始化doff_vec为0, 它的记录的单位是一个标签的每个维度
}
for( _int i=0; i<num_X; i++ ) // 遍历每个标签
{
for( _int j=0; j<size[i]; j++ ) // 遍历每个标签的特征 (size[i]表示第i个标签实际具有的非0元个数)
{
_int lbl = data[i][j].first;// 取得当前特征实际的下标(于实际邻接矩阵中)
_float val = data[i][j].second * idcgs[i];
// 计算I_{L}(y_i)y_i
if(pos_or_neg[i]==+1)
pos_sum[lbl].second += val;
else
neg_sum[lbl].second += val;
}
}
new_ndcg = 0;
// s \in {-1, +1}
// for循环1
for(_int s=-1; s<=1; s+=2) // 选定分区, 确定一个δ_i
{
VecIF& sum = s==-1 ? neg_sum : pos_sum;
// sort按值排序这个过程就是贯彻论文中的rank_L
// 对一个标签内部排序的前num_Y(也就是L)个信息排序
sort(sum.begin(), sum.begin()+num_Y, comp_pair_by_second_desc<_int,_float>);
// 到目前为止, sum这个长度为L(num_Y)的整合标签的lbl顺序, 就是论文中提到的最好r+和r-(是+/-看s的取向)
// 下面是计算最好的NDCG
for(_int i=0; i<num_Y; i++) // 逐特征遍历
{
_int lbl = sum[i].first;
_float val = sum[i].second;
diff_vec[lbl] += s*discounts[i];// 见注1
new_ndcg += discounts[i] * val; // 计算出全局的NDCG
}
}
new_ndcg /= num_X; // 对全局NDCG进行取均值得到每个标签的平均NDCG
// for循环2
for( _int i=0; i<num_X; i++ ) // 先选择一个标签
{
_float gain_diff = 0;
for( _int j=0; j<size[i]; j++ ) // 后遍历这个标签的维度
{
_int lbl = data[i][j].first;
_float val = data[i][j].second * idcgs[i];
// 计算I_{L}(y_i)y_i
gain_diff += val*diff_vec[lbl]; // 见注2
}
if(gain_diff>0) // sign(gain_diff)>0
pos_or_neg[i] = +1; // set δ_i = +1
else if(gain_diff<0) // sign(gain_diff)<0
pos_or_neg[i] = -1; // set δ_i = -1
}
if(new_ndcg-ndcg<eps)
break;
else
ndcg = new_ndcg;
}
pairII num_pos_neg = get_pos_neg_count(pos_or_neg);
if(num_pos_neg.first==0 || num_pos_neg.second==0) // 正区和负区不可能一个都没有
return false;
return true;
}
为了方便描述, 这里我们将这段代码最外层的四个for循环的后两个分别称之为for循环1和for循环2
-
代码中的discount数值是 I D C G IDCG IDCG求和的拆开一部分, 源码中的表现如下:

可以认为. 我们用变量存储了这种对应 discount[i] <=> 1 log ( 1 + i ) \frac{1}{\log(1+i)} log(1+i)1
你可以认为他是 D C G DCG DCG的分母, 当然若你能理解地更进一步, 你可以认为他是一个关联 i i i顺序的式子, i i i越小, 越靠前, 1 log ( 1 + i ) \frac{1}{\log(1+i)} log(1+i)1越大. -
注释1:
diff_vec[lbl] += s * discounts[i]这里使用discount, 如果我们按照上面的定义替换就可以将这里的代码视为公式: δ i l o g ( 1 + l ) \frac{\delta_i}{log(1+l)} log(1+l)δi 这里如果 s = − 1 s=-1 s=−1, 那么后面分式的分子就是 δ i = − 1 \delta_i = -1 δi=−1, 反之亦然. 但是要注意这里对于diff_vec的访问下标是lbl, 这个lbl的访问顺序其实就是最佳 r ± \mathbf{r}^{\pm} r±的顺序, 因此这里的目的将 r ± \mathbf{r}^{\pm} r±的内容用 δ i l o g ( 1 + l ) \frac{\delta_i}{log(1+l)} log(1+l)δi的形式表示出来. 这种逻辑可见下图: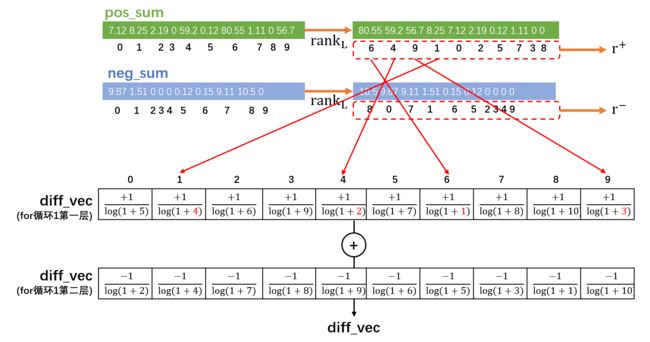
为何要把 r ± \mathbf{r}^{\pm} r±用如此麻烦的形式表现出来? 原因是 r ± \mathbf{r}^{\pm} r±本身的顺序性.
r ± \mathbf{r}^{\pm} r±是通过各自正(负)区标签求和并再排序得到的一种抽象的, 全局的参数. 但是, 我们实际在计算一个标签的 D C G DCG DCG的时候是很难与它联系起来. 前者是一种需要全局学习得到的产物, 而后者是局部的问题.
于是作者巧妙认为, D C G DCG DCG是一种基于排序的评价指标, 因此在标签排序之后计算的 D C G DCG DCG的分母中是持有了这次排序信息的. 于是我们保留排序后的 D C G DCG DCG分母并且把 D C G DCG DCG分母参数藏到对应的标签每个维度项中; 后续在探讨一个未排序过的单个标签的有序时的 D C G DCG DCG的时候, 对于任意维度项 y i k y_{i k} yik, 我们都可以知道在排序后它的位置对应的累加 D C G DCG DCG的分母部分 log ( 1 + k r + ) \log(1+k_{\mathbf{r}^+}) log(1+kr+), 从而在未排序的情况下直接累加这个 D C G DCG DCG的子项 y i k log ( 1 + k r + ) \frac{y_{i k}}{\log(1+k_{\mathbf{r}^{+}})} log(1+kr+)yik. 所以, 从相对运动的角度来看, 求 D C G DCG DCG可以看做是所有项排序后, 分子保持新序, 然后分母从 log ( 1 + 1 ) \log(1+1) log(1+1)到 log ( 1 + L ) \log(1+L) log(1+L); 同时, 也可以看做分子保持原有顺序, 然后分母从 log ( 1 + a 1 ) \log(1+a_1) log(1+a1)到 log ( 1 + a L ) \log(1+a_L) log(1+aL), 这里 { a 1 , a 2 , … , a L } \{a_1, a_2, \dots,a_L\} {a1,a2,…,aL}是对应的原分子位置排序后处于的新位置.
此外, 因为diff_vec收集的是正(负)区的标签和向量的 log ( 1 + k r ± ) \log(1+k_{\mathbf{r}^{\pm}}) log(1+kr±), 因此diff_vec是一种全局学习的产物, 而单个标签的 D C G DCG DCG是局部的问题, 他关注的是一个具体问题. 通过单个标签排序并记录他的 log ( 1 + k r l o c a l ) \log(1+k_{\mathbf{r}_{local}}) log(1+krlocal)与通过多个标签排序并记录他的 log ( 1 + k r g l o b a l ) \log(1+k_{\mathbf{r}_{global}}) log(1+krglobal)是不同的. 这里作者采用全局学习的diff_vec来控制任何一个局部标签的 D C G DCG DCG计算.
另外不可忽视的地方在于: 这里将 正/负区标签和 的diff_vec进行了求和, diff_vec[l] (第 l l l个维度) 实际得到的是 − 1 log ( 1 + l r − ) + 1 log ( 1 + l r + ) (9) -\frac{1}{\log(1+l_{r^{-}})}+\frac{1}{\log(1+l_{r^{+}})} \tag{9} −log(1+lr−)1+log(1+lr+)1(9) l r − l_{r^{-}} lr−表示原本位于 l l l位置的维度项 y i l y_{i l} yil在排序 (依照负区的求和标签排序) 后的新位置下标. -
注释2:
gain_diff += val * diff_vec[lbl];这个语句利用了之前计算得到的每个标签的一个差信息diff_vec[lbl], 并且用标签本身的val ( v a l = I L ( y i ) y i r val = I_L(\mathbf{y}_i)y_{ir} val=IL(yi)yir)乘上了这个信息. 我们可以利用公式来辅助理解:
I L ( y i ) ∑ l = 1 L − y i r l − + y i r l + log ( 1 + l ) = I L ( y i ) ∑ l = 1 L ( − y i r l − log ( 1 + l ) + y i r l + log ( 1 + l ) ) (10) I_L(\mathbf{y}_i)\sum_{l=1}^{L} \frac{-y_{i r_{l}^{-}}+y_{i r_{l}^{+}}}{\log (1+l)} = I_L(\mathbf{y}_i)\sum_{l=1}^{L} \left( \frac{-y_{i r_{l}^{-}}}{\log (1+l) } + \frac{y_{i r_{l}^{+}}}{\log (1+l) }\right) \tag{10} IL(yi)l=1∑Llog(1+l)−yirl−+yirl+=IL(yi)l=1∑L(log(1+l)−yirl−+log(1+l)yirl+)(10)
这个公式难在代码中理解是因为公式的分母是以 l l l的自然增序, 分子 y i r l ± y_{i r_{l}^{\pm}} yirl±按照从大到小的顺序( r ± \mathbf{r}^{\pm} r±)排序得到的. 而代码中的diff_vec的是保持分子 y i l y_{i l} yil原序, 而分母被一定重排得到的 l r ± l_{r^{\pm}} lr±. 于是我们可以进一步按照公式9来修改这个公式为:
I L ( y i ) ∑ l = 1 L ( − y i l log ( 1 + l r − ) + y i l log ( 1 + l r + ) ) = ∑ l = 1 L ( I L ( y i ) y i l ) ( − 1 log ( 1 + l r − ) + 1 log ( 1 + l r + ) ) (11) \begin{aligned} I_L(\mathbf{y}_i)\sum_{l=1}^{L} \left( \frac{-y_{i l}}{\log(1+l_{r^{-}})}+\frac{y_{i l}}{\log(1+l_{r^{+}})}\right)\\ = \sum_{l=1}^{L} \left( I_L(\mathbf{y}_i) y_{i l}\right)\left( \frac{-1}{\log(1+l_{r^{-}})}+\frac{1}{\log(1+l_{r^{+}})}\right) \end{aligned}\tag{11} IL(yi)l=1∑L(log(1+lr−)−yil+log(1+lr+)yil)=l=1∑L(IL(yi)yil)(log(1+lr−)−1+log(1+lr+)1)(11)
l r − l_{r^{-}} lr−表示原本位于 l l l位置的维度项 y i l y_{i l} yil在排序 (依照负区的求和标签排序) 后的新位置下标.
l r + l_{r^{+}} lr+表示原本位于 l l l位置的维度项 y i l y_{i l} yil在排序 (依照正区的求和标签排序) 后的新位置下标.
公式10和11完全是等价的, 只不过我们的"参考系"不一样, 如果你有耐心举个小规模例子把两个求和展开, 可以发现他们只是相同项目换了顺序求和, 故事还是一个故事.
现在公式11就能非常完美地解释gain_diff += val*diff_vec[lbl];这里的gain_diff就是8式左半部分, 右半部分似乎作者没有在代码中表现出来. 我的猜测可能是作者默认设置了 C r = 1 , C δ = 0 C_r=1, C_\delta=0 Cr=1,Cδ=0. 因为文章中 r , δ i \mathbf{r}, \delta_i r,δi的拟合与 w \mathbf{w} w的拟合是分开进行的, 右边的 w \mathbf{w} w在这时无法固定为有效值, 可能在编程时把这部分合理地忽略了(猜测)
总结来, 注释1的代码藏在for循环1中, for循环1是对于正区标签和和负区标签和这两个向量的遍历, 自然是具有典型的全局性的, 因此我们用它来学习diff_vec, 用它来承载 r \mathbf{r} r拟合的结果. 而for循环2是对所有标签的遍历, 依次计算每个标签的gain_diff, 按照8式( C r = 1 , C δ = 0 C_r=1, C_\delta=0 Cr=1,Cδ=0)来看, 就是逐个学习第 i i i个标签的 δ i ∗ \delta_i^{*} δi∗, 代码中我们用pos_or_neg记录学习结果, 它有显然的局部性 (但是会利用全局的gain_diff).
if(gain_diff>0) // sign(gain_diff)>0
pos_or_neg[i] = +1; // set δ_i = +1
else if(gain_diff<0) // sign(gain_diff)<0
pos_or_neg[i] = -1; // set δ_i = -1
我们整个的optimize_ndcg方法就是一个极大的while循环, 假设上个回合是[t].
每回合都会在for循环1中基于以往的标签分区来求得正标签和/负标签和, 然后通过他俩各自的排序得的新的 r ± [ t + 1 ] \mathbf{r}^{\pm}[t+1] r±[t+1], 并且通过这两个向量的最佳排序求得全局 N D C G [ t + 1 ] NDCG[t+1] NDCG[t+1], 再归一化得到近似的单个标签平均 N D C G ‾ [ t + 1 ] \overline{NDCG}[t+1] NDCG[t+1]. 顺便在for循环2中给每个标签 i i i训练出新的新分区 δ i ∗ [ t + 1 ] \delta_i^*[t+1] δi∗[t+1]. 倘若当前回合得到的 N D C G ‾ [ t + 1 ] \overline{NDCG}[t+1] NDCG[t+1]相比上个回合的 N D C G ‾ [ t ] \overline{NDCG}[t] NDCG[t]的更新偏差足够小, 我们便认为当前对于 N o d e . i d Node.id Node.id的分区划分已经收敛. 否则我们会按照新的每个 i i i标签分区 δ i ∗ [ t + 1 ] \delta_i^*[t+1] δi∗[t+1]来开始下一回合的迭代.
if(new_ndcg-ndcg<eps)
break;
else
ndcg = new_ndcg;
上述while循环本质上是对 N o d e . i d Node.id Node.id的划分, 最终这些分区的0/1选择会指导树的形成. 自然, 如果某次optimize_ndcg方法返回所有的 N o d e . i d Node.id Node.id都划分为一个区, 那么树的划分将会陷入严重不平衡, 因此这种情况下应当认为当前结点不可划分, 应当将其标记为树叶. 在optimize_ndcg函数之中作者设置了这种问题的跳出机制.
pairII num_pos_neg = get_pos_neg_count(pos_or_neg);
if(num_pos_neg.first==0 || num_pos_neg.second==0) // 正区和负区不可能一个都没有
return false;
return true;
2.4.3 w \mathbf{w} w的优化与拟合
根据论文中的描述, w \mathbf{w} w的拟合似乎是一个非必要选项, 准确地说, 作者认为如果在 r \mathbf{r} r和 δ \delta δ拟合后loss都没有缩小的话, 那么才会对 w \mathbf{w} w进行拟合. 这样做的目的也是基于XML的巨量耗时做出的妥协, 因为关于 δ \delta δ和 r \mathbf{r} r的优化只需要几秒钟, 但是关于 w \mathbf{w} w的优化可能就需要几分钟!
这样选择性的拟合方案效果还是很不错的, 论文中作者还是狠狠地吹了这个效果的:
In practice, it was observed on all data sets that the algorithm made rapid progress and yielded state-of-the-art results as soon as a single update to w had been made
w \mathbf{w} w的拟合我并没有很细致地去看, 因为作者使用了newGLMNET算法对这部分进行优化, 这个算法是一个基于1-范数的逻辑回归问题 (也就是拟合3式中的第一项). 等今后有空再来完善这部分的解释.
G.-X. Yuan, C.-H. Ho, and C.-J. Lin. An improved glmnet for l1-regularized logistic regression. JMLR, 13:1999–2030, 2012.
他的拟合目标为:
min w ∈ R D ∥ w ∥ 1 + ∑ i C δ ( δ i ) log ( 1 + e − δ i w ⊤ x i ) (12) \min _{\mathbf{w} \in \mathcal{R}^{D}}\|\mathbf{w}\|_{1}+\sum_{i} C_{\delta}\left(\delta_{i}\right) \log \left(1+e^{-\delta_{i} \mathbf{w}^{\top} \mathbf{x}_{i}}\right)\tag{12} w∈RDmin∥w∥1+i∑Cδ(δi)log(1+e−δiw⊤xi)(12)
若说针对 r \mathbf{r} r与 δ \delta δ的拟合是针对标签进行的, 那么针对 w \mathbf{w} w的拟合是针对特征矩阵 X \mathbf{X} X进行的.
其中 C δ ( δ i ) C_{\delta}\left(\delta_{i}\right) Cδ(δi)是通过之前拟合的 δ i \delta_i δi而进行处理得到的一种系数. 具体见下列代码:
VecF C( num_X );
pairII num_pos_neg = get_pos_neg_count( pos_or_neg ); // 见注释1
_float frac_pos = (_float)num_pos_neg.first/(num_pos_neg.first+num_pos_neg.second); // 正区标签占比
_float frac_neg = (_float)num_pos_neg.second/(num_pos_neg.first+num_pos_neg.second); // 负区标签占比
_double Cp = param.log_loss_coeff/frac_pos;
_double Cn = param.log_loss_coeff/frac_neg; // unequal Cp,Cn improves the balancing in some data sets
for( _int i=0; i<num_X; i++ )
C[i] = pos_or_neg[i] == +1 ? Cp : Cn; // 给每个标签分配自己的区的C
注释1: get_pos_neg_count()返回了一个二元组构成的数组num_pos_neg, num_pos_neg.first表示 δ i = + 1 \delta_i=+1 δi=+1的个数, 也就是在刚刚进行的划分后确定的位于正区的实例 (或者说标签)的个数; num_pos_neg.second表示 δ i = + 1 \delta_i=+1 δi=+1的个数.
之后frac_pos与frac_neg分别计算了正区与负区的占比, 而后他们分别作为了 C p C_p Cp与 C n C_n Cn这两个参数的分母, 这里param.log_loss_coeff是一个用户定义的全局参数, 作者好像设定其默认为1.
直观来看, 当划分正区的比例越多的时候, C p C_p Cp好像会越小, C n C_n Cn好像会越大. 于是可以认为, 作者给每个实例分配的一个系数 C C C, 当这里实例所在分区的占比越低, 那么给他分配的这个权值系数将会越大. 因此某个实例 i i i的对应 C i C_i Ci肯定受到 δ i \delta_i δi的约束, 故论文中公式是 C δ ( δ i ) C_{\delta}(\delta_i) Cδ(δi).
后续源码给出具体关于 w \mathbf{w} w的优化 (optimize_log_loss( )函数) 我就没细看了, 以后阅读了newGLMNET算法之后再来看这个
success = optimize_log_loss( Xf_X, pos_or_neg, C, node->w, param );
if(!success)
return false;
(待续…)
2.5 树的训练
在随机森林中会对 T T T颗树进行训练.
在2.4中解决了三个参数拟合问题后, 自底向上地从源码入手, 我们来认识下对 T T T颗中某颗树的训练过程.
如果对代码细节不求甚解, 那么只用看2.5.1和2.5.3即可
2.5.2和2.5.4涉及一些稀疏矩阵的思想.
2.5.1 主体
Tree* train_tree( SMatF* trn_X_Xf, SMatF* trn_X_Y, Param& param, _int tree_no )
{
reng.seed(tree_no); // 按照tree_no(每个树的编号)为树生成为一个随机种子
_int num_X = trn_X_Xf->nc; // 实例数
_int num_Xf = trn_X_Xf->nr; // 特征数
_int num_Y = trn_X_Y->nr; // 标签维度
Tree* tree = new Tree; // 关于树的类
vector<Node*>& nodes = tree->nodes; // 得到数的结点队列(初始为空)
VecI X; // VecI表示vector容器, 生成int容器, 初始容器大小是0
for(_int i=0; i<num_X; i++)
X.push_back(i); // 生成根节点的n.Id
Node* root = new Node( X, 0, param.max_leaf );
// param.max_leaf这个参数在当前结点为叶子时才有用
nodes.push_back(root); // 根结点入队
VecI pos_or_neg; // 统计第i个实例分在哪个区
for(_int i=0; i<nodes.size(); i++) // nodes的会在后续的入队中不断变长
{
Node* node = nodes[i]; // 选择队首结点
VecI& n_X = node->X; // 用n_X存储n.Id
SMatF* n_trn_Xf_X;
SMatF* n_trn_X_Y; // 初始化两个压缩矩阵
VecI n_Xf;
VecI n_Y;
// 见注释1
shrink_data_matrices( trn_X_Xf, trn_X_Y, n_X, n_trn_Xf_X, n_trn_X_Y, n_Xf, n_Y );
if(node->is_leaf)
{
calc_leaf_prob( node, n_trn_X_Y, param );
// 见注释2
}
else // 若非叶, 那么就开始划分
{
VecI pos_or_neg;
bool success = split_node( node, n_trn_Xf_X, n_trn_X_Y, pos_or_neg, param );
// 对r和δ进行拟合优化, 详情见2.4.1, 2.4.2和2.4.3
// 最终δ优化结果存储在pos_or_neg中
if(success)
{
// 将n_X按照正负区划分为pos_X和neg_X
VecI pos_X, neg_X;
for(_int j=0; j<n_X.size(); j++)
{
_int inst = n_X[j];
if( pos_or_neg[j]==+1 )
pos_X.push_back(inst);
else
neg_X.push_back(inst);
}
// 正区设置结点, 为左儿子, 深度为+1, param.max_leaf为额定参数
Node* pos_node = new Node( pos_X, node->depth+1, param.max_leaf );
nodes.push_back(pos_node);
// 入队(for循环周期变长)
node->pos_child = nodes.size()-1;
// 负区设置结点, 为右儿子, 深度为+1, param.max_leaf为额定参数
Node* neg_node = new Node( neg_X, node->depth+1, param.max_leaf );
nodes.push_back(neg_node);
// 入队(for循环周期变长)
node->neg_child = nodes.size()-1;
}
else // 对于不可分点, 标记为叶子, 交给下一回合来处理
{
node->is_leaf = true;
i--; // 下回合重新审视
}
}
postprocess_node( node, trn_X_Xf, trn_X_Y, n_X, n_Xf, n_Y );
// 见注释3
delete n_trn_Xf_X; // 临时变量清空
delete n_trn_X_Y;
}
tree->num_Xf = num_Xf;
tree->num_Y = num_Y;
return tree;
}
2.5.2 shrink_data_matrices函数 (注释1)
shrink_data_matrices()函数是个非常麻烦的函数, 初次看的时候要捋清楚不是一件容易的事, 但是这里我尽量用简单的语言说清楚.
简单来说, 他是一个对稀疏矩阵进行调整的函数. (他和FastXML关系不大,但是我感觉为了方便阅读代码, 还是要大概知道它的作用, 不然很多地方可能会看不懂 )
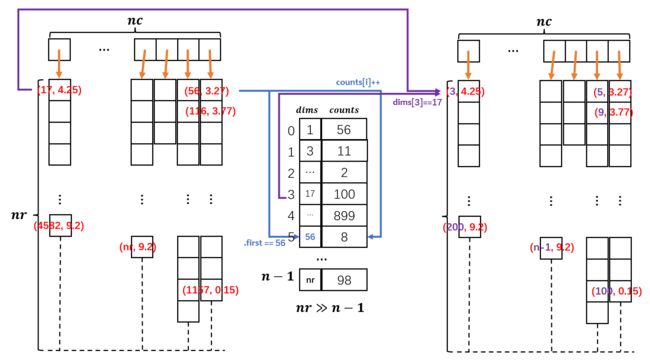
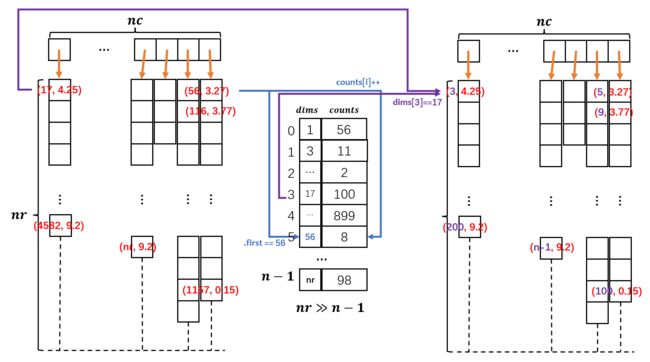
图中左侧的稀疏矩阵是本篇论文源代码采用的存储方式, nc代表列数, nr代表行数.
源文件中的数据是稀疏的, 其中涉及的实际每列数据往往不是连续存在的:

因此我们用物理上连续的二元组来存储他们, 然后用二元组的first部来存储逻辑下标 (例如上上图中的17, 56, 116 … 这些)
要注意一些细节:
- 每列的数组长度基本上是不可能达到标准列长 n r nr nr的, 因为这是个稀疏矩阵
- 每列的数组的单个数据项中的first部分存储的值是可能是 1 1 1到 ( n r − 1 ) (nr-1) (nr−1)的任意一个数
但是实际上这些维度虚拟的逻辑下标难以管理, 因为这些下标的不连续导致了我们很难提供一个连续的存储结构来构造快捷的映射.
例如第 k k k列的虚拟下标是(nr-100), 要找它的位置我们必须对 k k k列进行遍历, 逐一判断每项是否first == (nr-100)?
于是作者打算把所有列的虚拟下标全部排个序, 要是某些虚拟下标重复了就记录到counts里面表示此虚拟下标重复了几次.
于是就得到了中间那个dims和counts数组.
当然, 其实这个数组还有一些潜在的价值性, 例如: dims的长度 n n n表示了 这个稀疏矩阵中实际存储的 有非零元素 的行的个数. 比方说, 图中dims中没有2, 那么证明这个稀疏矩阵的第2行是全0的. 因此dims在逻辑上也有更进一步压缩矩阵信息的功能.
最后我们将所有的虚拟下标改为dims对应的索引下标, 这就是图中最右边的表. 如此一来, 每当我们要查询第 k k k列中的第 q q q行, 便可直接通过dims[q]来检索. 同时也可以很轻松利用这个表查询到原虚拟下标的值.
shrink_data_matrices( )函数的功能:
输入:
trn_X_Xf: 原稀疏数据矩阵 X \mathbf{X} X;
trn_X_Y: 原稀疏标签矩阵 Y \mathbf{Y} Y;
n_X: 选择的 n . I d n.Id n.Id, 这些 I d Id Id对应为稀疏矩阵的列;
输出:
n_trn_Xf_X: 处理后的稀疏数据矩阵 X ′ \mathbf{X}^{\prime} X′;
n_trn_X_Y: 处理后的稀疏标签矩阵 Y ′ \mathbf{Y}^{\prime} Y′;
n_Xf: 这个就是图中的dims, 只不过他是属于数据矩阵的
n_Y: 这个就是图中的dims, 只不过他是属于标签矩阵的
就作者给出的源码中附带的数据库EUR-Lex来说, 原稀疏数据矩阵是 X \mathbf{X} X是15539 × \times × 5000的, 对以根节点为基础的 n . I d n.Id n.Id处理之后从 n r nr nr中提取出了 n n n, 变为逻辑上15539 × \times × 5000的矩阵 (是的, 没有变化! 是存在所有Id都平均占有所有特征的情况); 原稀疏标签矩阵是 Y \mathbf{Y} Y是15539 × \times × 3993的, 对以根节点为基础的 n . I d n.Id n.Id处理之后从 n r nr nr中提取出了 n n n, 变为逻辑上15539 × \times × 3786的矩阵

这就像上面这个有5行数据的矩阵, 如果我选择列集合={0,1,2,3,4,5,6}, 那么这5行都是有效的.
但是如果我们改为选择列集合={0,1,2,3,4,5}, 那么倒数第2行就变得无意义了. 在压缩化矩阵里面, 我们其实有效存储的长度就变成4行. 这个5->4就是上述 Y \mathbf{Y} Y从3993到3786变化的本质.
倘若你选择列集合{0,1,6}, 最终这5行都还是有效行, 因此5->5保存不变. 这就是 X \mathbf{X} X从5000到5000变化的本质.
因此!!
shrink_data_matrices( )函数对于稀疏矩阵的调整极大程度受到变量n_X的影响! 也就是 n . I d n.Id n.Id
2.5.3 calc_leaf_prob函数 (注释2)
这个函数是在当前结点判定为叶子结点的时候进行的操作
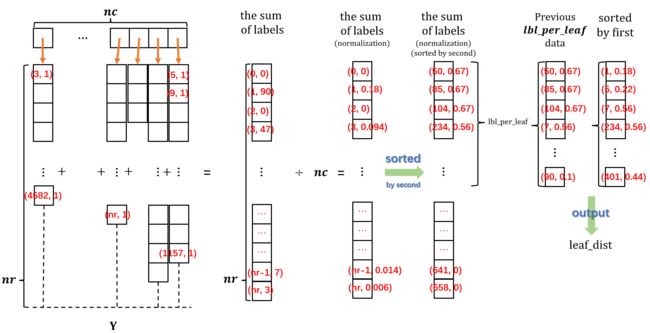 当我们判定当前结点是叶子结点时候就进行上面这样的操作.
当我们判定当前结点是叶子结点时候就进行上面这样的操作.
- 通过当前结点的 n . I d n.Id n.Id(这个时候 n . I d n.Id n.Id往往满足 ∣ n . I d ∣ < < ∣ r o o t . I d ∣ |n.Id|<<|root.Id| ∣n.Id∣<<∣root.Id∣) 和 ( X ′ , Y ′ ) (\mathbf{X}^{\prime},\mathbf{Y}^{\prime}) (X′,Y′)对应关系查询到当前 n . I d n.Id n.Id对应的标签矩阵 Y ′ \mathbf{Y}^{\prime} Y′
- 对标签的标签求和. 需要注意, 这里的单个标签是采用稀疏方式存储的, 因此任何一个标签的长度都是远小于 n r nr nr的; 而求和的标签和采用的是长度为 n r nr nr的一个数组存储. 因此这个数组必然是一个稀疏的, 有许多项的second部分都是0.
- 对长度为 n r nr nr的 标签和 的每个second项依次除以标签个数 n c nc nc, 即归一化. 言下之意就是用这一个标签 来代表这 n c nc nc个标签的平均标签特征分布.
- 对这个标签按照second值从大到小排序, 并且截取前lbl_per_leaf个标签特征.
- 再对这个截取后的长度为lbl_per_leaf标签按照每项的first从大到小排序, 即恢复原来的顺序.
4, 5步可以理解为保留原长度为 n r nr nr的归一化标签中那些归一化值排在前lbl_per_leaf的标签特征, 然后删去其他标签特征, 从而的得到一个新的长度为lbl_per_leaf的标签
论文中, 我们把最终这样提取出来的标签叫做 P leaf \mathbf{P}^\text{leaf} Pleaf
理论上, 一个叶子结点会对应一个 P leaf \mathbf{P}^\text{leaf} Pleaf
而如果我们在一个建立完善的树的树根丢进去一个测试示例 x \mathbf{x} x, 最终 x \mathbf{x} x顺着树的结构落到了一个叶子上, 我们就成这个叶子对应一个标签 P leaf ( x ) \mathbf{P}^\text{leaf}(\mathbf{x}) Pleaf(x), 这个就是后面预测的故事了.
下面给出calc_leaf_prob代码
void calc_leaf_prob( Node* node, SMatF* X_Y, Param& param ) // 带入的X_Y是标签矩阵
{
_int lbl_per_leaf = param.lbl_per_leaf;
_int num_X = X_Y->nc; // 标签数目
_int num_Y = X_Y->nr; // 标签的最大维度
_int* size = X_Y->size; // size存储了一个数组, 每项表示了一个标签的长度
pairIF** data = X_Y->data; // data存储了一个指针数组, 其中每一个指针都指向一个标签数组
VecIF& leaf_dist = node->leaf_dist; // leaf_dist采用node中leaf_dist变量的地址
leaf_dist.resize( num_Y );
for( _int i=0; i<num_Y; i++ )
leaf_dist[i] = make_pair( i, 0 );
for( _int i=0; i<num_X; i++ ) // 选择一个标签
{
for( _int j=0; j<size[i]; j++ ) // 选择这个标签的每个维度
{
_int lbl = data[i][j].first; // 取出虚拟下标
_float val = data[i][j].second;
leaf_dist[lbl].second += val; // 标签求和
}
}
// 下面是计算叶子结点的标签P^{leaf}
for( _int i=0; i<num_Y; i++ )
leaf_dist[i].second /= num_X; // 归一化
sort( leaf_dist.begin(), leaf_dist.end(), comp_pair_by_second_desc<_int,_float> );
if( leaf_dist.size()>lbl_per_leaf )
leaf_dist.resize( lbl_per_leaf );
sort( leaf_dist.begin(), leaf_dist.end(), comp_pair_by_first<_int,_float> );
}
2.5.4 postprocess_node函数 (注释3)
这个函数是个尾处理, 是2.5.2的逆过程, 前面我们将稀疏矩阵换成了第二个版本 (见2.5.2中的第一张图), 这个版本中的虚拟下标被替换为我们基于所有虚拟下标排序后重新设定的新下标, 而这个新下标并不是真正的矩阵下标, 在后续预测阶段无法使用这些资料. 因此在当前结点训练完成的时候, 我们这些结点的相关的下标还回去.
我们实际上只需要还原每个叶子结点的 P leaf \mathbf{P}^\text{leaf} Pleaf标签和常规结点的 w \mathbf{w} w就好了, 因为这些内容才是预测阶段会实际用到的.
void postprocess_node( Node* node, SMatF* trn_X_Xf, SMatF* trn_X_Y, VecI& n_X, VecI& n_Xf, VecI& n_Y )
{
if( node->is_leaf )
reindex_VecIF( node->leaf_dist, n_Y ); // n_Y为标签矩阵的dims, 重新映射每个标签特征真正对应的特征下标
else
reindex_VecIF( node->w, n_Xf ); // n_Xf为数据矩阵dims, 重新映射w对应的真正实例
}
void reindex_VecIF( VecIF& vec, VecI& index )
{
for( _int i=0; i<vec.size(); i++ )
vec[i].first = index[ vec[i].first ];
return;
}
可以参考之前的下面这个图 (这个图就是2.5.2中的第一张图) 来理解这个逆过程, 代码中的index就是下图的dims.
这里的reindex_VecIF()目的即将图右侧的某一个标签 k k k变为左侧的标签 k k k
2.6 基于训练完毕的树模型来进行数据预测
相比训练, 基于模型来进行预测要简单一些.
首先不能忘了, FastXML是基于随机森林算法的, 因此我们会训练 T T T颗不同随机种子的树, 这些树的根节点虽然都是完整的 n . I d n.Id n.Id, 但是因为种子分配的随机性, 这些根的初始正负划分完全不同, 因此伴随算法的推进, 它们最终会长成 T T T颗迥然不同的树.
而预测的目标类似于集成学习, 我们每次选择一个预测样例 x \mathbf{x} x丢到一棵树中都能得到一个近似的预测, 那么将其丢到 T T T颗树组成的森林中的话, 最终就能得到 T T T个相关预测. 最后我们将这 T T T个预测进行一次集成即可得到对于 x \mathbf{x} x的较为精确的预测.
2.6.1 预测数据在单个树中的决策
预测数据 x i \mathbf{x}_i xi在进入某个结点后, 其会与这个结点的 w \mathbf{w} w进行内积运算.
这个操作, 源码中是通过test_svm()函数实现的
输入:
X_Xf是输入的测试集 X \mathbf{X} X;
w是当前结点的 w \mathbf{w} w;
X是当前结点的实例Id集, 相当于 n . I d n.Id n.Id
输出:
values: 存储每个实例对应的内积结果
整个过程的图描述:
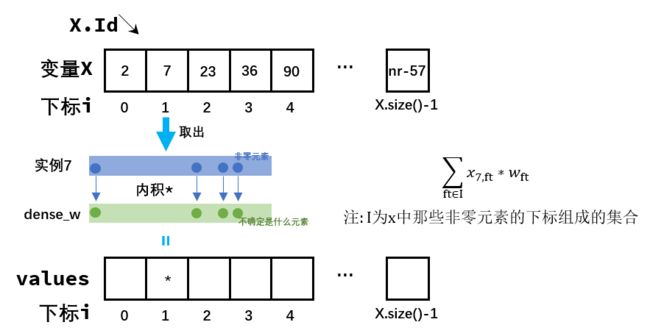
void test_svm( VecI& X, SMatF* X_Xf, VecIF& w, VecF& values )
{
values.resize(X.size());
// 若要存储每个实例对应的内积结果, 那么其长度为nr
_int num_Xf = X_Xf->nr; // 实例的最大维度
for(_int i=0; i<w.size(); i++)
// dense_w是一个全局变量, 他的长度是实例的最大额定特征长度
// w是一个压缩后的数组, 因此它的长度很短
dense_w[w[i].first] = w[i].second; // 压缩还原, 见注释1
_int* siz = X_Xf->size;
pairIF** data = X_Xf->data;
for(_int i=0; i<X.size(); i++)
{
_int inst = X[i]; // 选择一个实例inst
_float prod = 0;
for(_int j=0; j<siz[inst]; j++)
{
_int ft = data[inst][j].first; // 取出实例inst中那些非零值特征的下标
_float val = data[inst][j].second;// 取出实例inst中那些非零值
prod += val*dense_w[ft]; // 进行内积操作
}
values[i] = prod; // 内积结果保存下来, 与X保持映射的方式保存
}
for(_int i=0; i<w.size(); i++)
dense_w[w[i].first] = 0; // 因为dense_w是全局变量, 为了下次结点使用, 这里要清空
}
注释1: 将压缩后的w存储到dense_w中, 但是要注意, n r > > ∣ w ∣ nr>>|\mathbf{w}| nr>>∣w∣, 因此移植后, dense_w是极其稀疏的

抽象这个过程, 我们把预测矩阵 X \mathbf{X} X输入了一个结点 n n n的黑盒, 最终我们得到了一个values数组, 这个数组与我们 X \mathbf{X} X的 n . I d n.Id n.Id是一一对应的, 因此我们可以轻易查询到某个实例 k k k的values值, 而 sign ( values [ k ] ) \text{sign}(\text{values}[k]) sign(values[k])的二元取值就决定了我们当前 X \mathbf{X} X应当进入左孩子还是右孩子. 代码核心如下:
if(!node->is_leaf)
{
VecI& X = node->X;
test_svm(X, tst_X_Xf, node->w, values); // 对当前n.Id进行预测, 得到values
for( _int j=0; j<X.size(); j++ )
pos_or_neg[j] = values[j]>=0 ? +1 : -1; // values转换为二值pos_or_neg
Node* pos_node = nodes[node->pos_child];
// 左右儿子的X要清空, 因为其中仍然保存的是训练数据的实例集, 预测时我们会用新的测试数据去替换它们
// 这样完成一个数的测试后, 树中的信息就都是预测数据的, 方便集成
pos_node->X.clear();
Node* neg_node = nodes[node->neg_child];
neg_node->X.clear();
for(_int j=0; j<X.size(); j++) // 分割正负集
{
if(pos_or_neg[j]==+1)
pos_node->X.push_back(X[j]); // X被拆分, 但是数据也向树的更深一层下移了
else
neg_node->X.push_back(X[j]);
}
}
else // 如果X移动到了叶子结点
{
VecI& X = node->X;
VecIF& leaf_dist = node->leaf_dist;
_int* size = tst_score_mat->size; // tst_score_mat是一个特殊矩阵, 见注释1
pairIF** data = tst_score_mat->data;
for(_int j=0; j<X.size(); j++)
{
_int inst = X[j]; // 取出任一一个实例inst
// 将tst_score_mat中的inst实例的位置设置为当前叶子的P^{leaf}
size[inst] = leaf_dist.size();
data[inst] = new pairIF[leaf_dist.size()];
for(_int k=0; k<leaf_dist.size(); k++)
data[inst][k] = leaf_dist[k];
}
}
注释1:
我们会为每颗树分配一个独立的tst_score_mat, tst_score_mat的目的在于记录每个落入叶子结点的实例被分配到的 P leaf \mathbf{P}^{\text{leaf}} Pleaf.
具体来说, 当训练集 X \mathbf{X} X输入到模型中, 预测后, X \mathbf{X} X中不同的实例 x i \mathbf{x}_i xi可能会落入不同的叶子结点. 因此能确定的是, ∀ x i ∈ X \forall \mathbf{x}_i \in \mathbf{X} ∀xi∈X总会在模型的某个叶子 leaf k \text{leaf}_{k} leafk上找到, 而倘若这个 x i ∈ leaf k \mathbf{x}_i\in \text{leaf}_{k} xi∈leafk, 那么必然可以找到 x i \mathbf{x}_i xi所属叶子结点 leaf k \text{leaf}_{k} leafk的向量 P leaf k \mathbf{P}^{\text{leaf}_k} Pleafk. 故认为在测试集 X \mathbf{X} X中, ∀ x i ∈ X \forall \mathbf{x}_i \in \mathbf{X} ∀xi∈X输入到模型 f f f中, 总会得到映射: f : x i → P leaf k f: \mathbf{x}_i \rightarrow \mathbf{P}^{\text{leaf}_k} f:xi→Pleafk.
tst_score_mat就是用于记录这种映射的. 此外, 如此统一记录也会极大方便后续的 集成.
假定 X \mathbf{X} X是 n × d n \times d n×d, Y \mathbf{Y} Y 是 n × l n \times l n×l, 那么这个特殊的tst_score_mat的维度就是 n × l n \times l n×l的矩阵, 设定上, 它同 Y \mathbf{Y} Y大小一致. 如此设置的原理很简单: 1.需要记录所有实例, 因此有个 n n n; 2.所有 ∣ P leaf ∣ < l |\mathbf{P}^{\text{leaf}}|
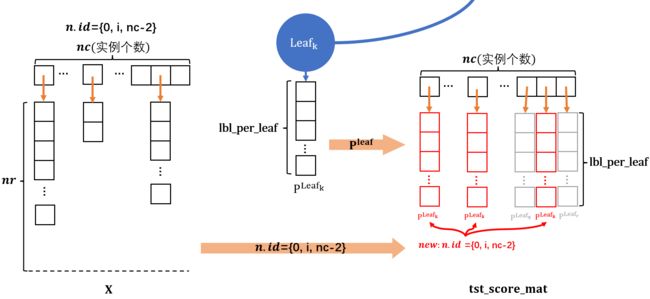
代码中, 对于单个叶子, 若测试数据落到了叶子结点, 得到测试数据的 n . I d n.Id n.Id, 那么将tst_score_mat中的那些契合 n . I d n.Id n.Id的列设置为当前叶子结点的 P leaf \mathbf{P}^{\text{leaf}} Pleaf. 当我们对每个叶子结点如此操作, 那么tst_score_mat的所有列就会刚好填满且不重复.
详见下图:
(下图tst_score_mat中的红色列为根据当前 n . I d n.Id n.Id新添加的列, 而灰色的是之前的列, 它们是其他叶子结点添加上去的. 另外要注意的一点就是实际的某些 P leaf \mathbf{P}^{\text{leaf}} Pleaf是可能小于lbl_per_leaf的, 因为训练阶段的某些Id选择下的叶子结点标签和的维度是可能比lbl_per_leaf还小的)
2.6.2 多个树预测的集成
多个树的集成在论文中是以下面这个公式呈现的: r ( x ) = rank k ( 1 T ∑ i = 1 T P i leaf ( x ) ) (13) \mathbf{r}(\mathbf{x})=\operatorname{rank}_{k}\left(\frac{1}{T} \sum_{i=1}^{T} \mathbf{P}_{i}^{\text {leaf }}(\mathbf{x})\right)\tag{13} r(x)=rankk(T1i=1∑TPileaf (x))(13)这里的 P i leaf ( x ) \mathbf{P}_{i}^{\text {leaf }}(\mathbf{x}) Pileaf (x)代表的就是某个实例 x \mathbf{x} x在第 i i i颗树中决策到一个确定的叶子之后, 得到的那个 P leaf ( x ) \mathbf{P}^{\text {leaf }}(\mathbf{x}) Pleaf (x), 因为这是第 i i i颗树干的好事, 因此记为 P i leaf ( x ) \mathbf{P}_i^{\text {leaf }}(\mathbf{x}) Pileaf (x). 然后我把这样的操作重复到 T T T颗树中, 最终将得到 T T T个 P i leaf ( x ) \mathbf{P}_i^{\text {leaf }}(\mathbf{x}) Pileaf (x)求和取平均
作者的思想是先确定一个总的线程数 T h Th Th和总的树的个数 t t t, 基本有 t > T h t>Th t>Th. 然后 t T h \frac{t}{Th} Tht表示每个线程分的树的个数, 作者的目的在于设置多线程来训练模型来优化速度, 让每个线程来分摊对于树的训练
下面的代码是一个线程中进行多个树的预测过程, 这里的t表示一个线程分配的树的个数, s代表当前线程分配的第一个树的序号
for(_int i=s; i<s+t; i++) // 确定一个当前树的序号i
{
...
Tree* tree = new Tree( model_dir, i ); // mode_dir是训练后的模拟所在的存储文件地址
...
SMatF* tree_score_mat = predict_tree( tst_X_Xf, tree, param );
// 获得这颗树的tree_score_mat, 这就是这颗树的最终预测成果
{
...
score_mat->add(tree_score_mat); // 把每棵树的tree_score_mat求和, score_mat是一个在外部定义的变量
...
}
delete tree;
delete tree_score_mat; // 删除局部变量
...
}
上述内容中, 我们将此线程中的每颗树的tree_score_mat加到了score_mat中, 此操作作用于每个线程, 就可将 T T T颗树的tree_score_mat全部加起来得到score_mat. 最终我们再对总和矩阵score_mat除 T T T就可得到均值分摊的score_mat
这里的score_mat就是我们最终预测的结果.
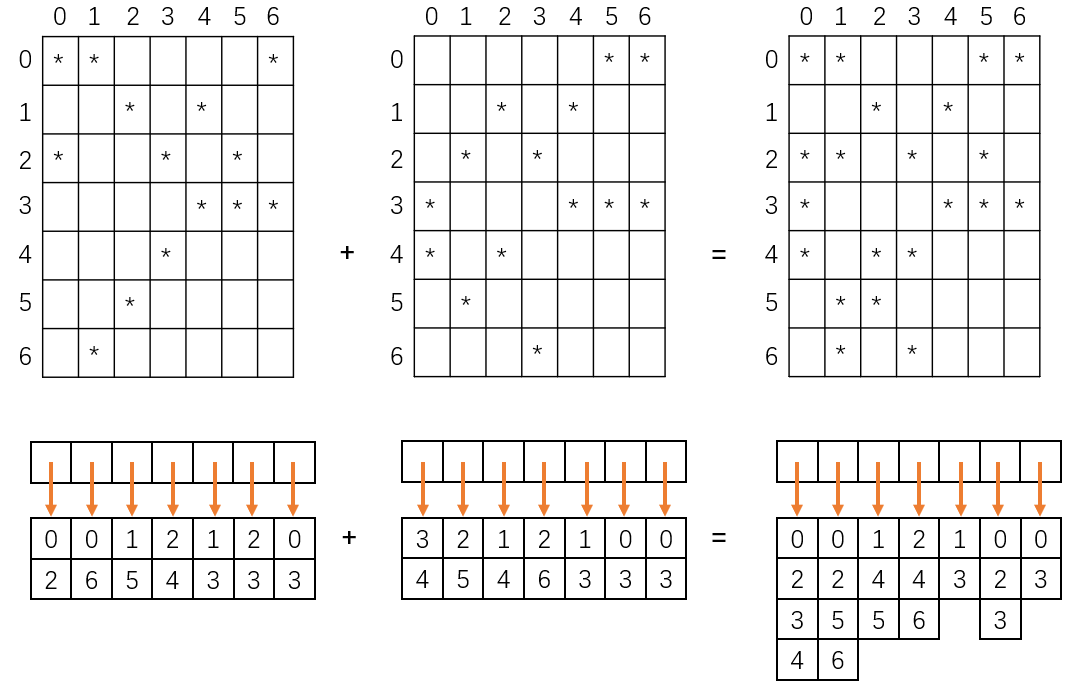
这里有个非常容易忽视的细节: 单颗树的tree_score_mat每列维度是不会超过lbl_per_leaf, 但是不可忽视的是, tree_score_mat每列的表示仍然是稀疏的压缩表示, 而对于压缩矩阵求和本质上是对于虚拟标签求和, 因此两个不同树的tree_score_mat求和得到的新tree_score_mat的某些列是可以超过lbl_per_leaf的. 下面就是一个鲜活的例子, 了解即可 (下面的压缩矩阵的每列都是2, 但是相加后有超过2的情况存在)
因此, 我们最终预测的score_mat矩阵本质上一个稀疏的 n × l n \times l n×l矩阵.
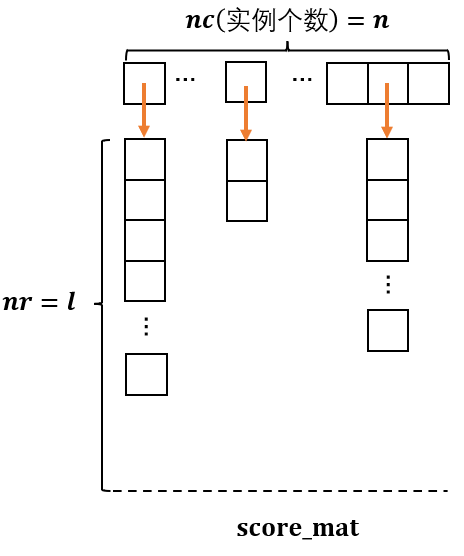
我的这篇分析喜欢用上图的转置+压缩存储的方式来形象表示这个矩阵( n c = n , n r = l nc=n, nr=l nc=n,nr=l), 在这样的表示中, 压缩矩阵的每一列都表示原 n × l n \times l n×l矩阵中的一个 1 × l 1\times l 1×l行. 这样的表示也是作者在源码中的表示方式.
我试着跑出作者提供的EUR-Lex数据集的score_mat矩阵, 然后随便查看了其中的一列(见下图), 与数据集的 Y \mathbf{Y} Y标签维度一比( l = 3993 l=3993 l=3993), 确实要稀疏太多了!
稀疏的score_mat矩阵若确定, 我们就可以与 Y \mathbf{Y} Y一道进行基本预测了.
同时, 若对score_mat和 Y \mathbf{Y} Y进行排名比较, 也可以应用一些基于评价指标例如Peak F 1 F_1 F1-score, A U C AUC AUC, N D C G NDCG NDCG.
这些内容相对容易, 不再赘述.
3.FastXML的总结与思考
FastXML的代码陆陆续续大概花了一周时间看完, 但是整理思绪写这篇总结花了大量时间, 中途因为开学到校, 上课, 处理课程等等事件拖了快一个多月了…
中途有几次拖了很长时间后, 回过头再写CSDN的时候关于代码和公式的细节都忘了{{{(>_<)}}}
所以我感觉能静下心读论文和写文章还是需要一个稳定的外部环境啊
咳咳, 不多说这些. 总结来看, FastXML是一个非常高效的处理多标签的算法.
它灵活运用了压缩矩阵的思想, 然后在很多地方用了些独具匠心的点子:
- FastXML在训练阶段分割结点的左右子树的时候采用的NDCG思路是很不错.
- 作者在代码中非常喜欢对多个标签的 “和” 进行操作, 或者说对 “求和后再求均值” 的标签操作. 实际上, XML的标签太多太多了, 这样求和后再判断标签特征的操作是非常节省时间的. 而且这样的操作是具有实际意义的: 相当于最开始, 我们是从全局的角度来考虑全部标签的特征, 而后这些提取的特征再一个个作用在每个标签上, 这就是全局特征的局部化.
这个思想非常鲜明地体现在作者 在训练模型时 对于一个结点的实例正负划分之中. - 在模型测试的时候, 作者用 w \mathbf{w} w与测试数据集 X \mathbf{X} X的每个实例的内积来判断测试数据的每个实例的正负性, 用种类似于SVM的方式来对测试数据实例进行决策是非常节约时间的. 只是可惜没时间去看相关的论文了, w \mathbf{w} w的拟合过程暂时没懂(待补).
- 交替最小化学习是个很好的方法, w \mathbf{w} w拟合花时间就先处理 r \mathbf{r} r和 δ \delta δ. 或者更甚, 若 r \mathbf{r} r和 δ \delta δ拟合后就能取得改进就放弃 w \mathbf{w} w拟合, 否则再拟合.
- matlab不一定慢. 多种语言混合编写也许能起到1+1>2的效果. 原作者是采用C++写的训练与测试, 但是评价指标与启动都是用matlab完成的. 我用VS编译器跑C++的速度是要慢于matlab作为启动器去启动C++程序的. 具体原因有待研究, 但是据观察, 好像matlab是将数据先放到电脑的cache缓存中再去读的? 这也许是一些可实现加速读取的方案.
- 用多线程总是会快些. 对于XML尽可能要去多用些这些技术
此外我也有些疑问.
是否其他基于排序的评价指标也可以应用到训练时的正负分区划分中? 似乎在逻辑上可以? 但我感觉需要注意的一个问题, N D C G NDCG NDCG是若干排序评价指标中计算实现简单的, 很大程度, N D C G NDCG NDCG中的变量很少且与排序直接相关. 但是 A U C AUC AUC, F 1 F_1 F1在参数上引入了混沌矩阵的相关参数, 他们是否与排序直接相关? 我感觉, 这些参数应用于拟合目标的研究还需要更多的数学技巧去证明的推演, 另外推演意义上合理的结果是否能程序化呢? 这些我暂且不清楚.
文中有些问题欢迎指出