概率论与数理统计学习：随机向量（一）——知识总结与C语言实现案例

hello，大家好

这里是第六期概率论与数理统计的学习。我将用这篇博客去整理知识点并在最后用C语言去实现具体案例。

本期知识点：

1. 随机向量的引入
2. 二维随机向量及其分布函数
3. 二维离散型随机变量

下面进入知识总结环节

随机向量

我们知道，随机变量是一个单值函数，也就是一个自变量对应于一个因变量。同C语言中的变量一样，一个变量只能有一个值。

在前面的一些随机试验中，我们常常是用一个随机变量来描述的，但有些随机现象只用一个随机变量来描述是往往不够的。例如，在打靶时，我们需要知道子弹在靶上的位置，可以将靶看作一个平面，然后子弹的位置就是这个平面上的一个点，也就是需要两个坐标来确定。那么这时，就需要两个随机变量了。

由向量的定义我们也可以知道。向量是有方向和大小的。一个点能有方向和大小吗？答案是否定的。到这里，我相信大家也清楚了随机向量的概念。

定义：

一般地，对某一个随机试验涉及的$n$个随机变量$X_1,X_2,...,X_n$，记为$(X_1,X_2,...,X_n)$，成为$n$维随机向量或$n$维随机变量。

二维随机向量及其分布函数

上面我们说到，一个平面上的坐标可以由两个随机变量组合表示。那么可以知道这两个随机变量的取值一定是在这个平面范围内的，也就是说二位随机向量$(X,Y)$中的两个随机变量$X$和$Y$是有联系的，它们是定义在同一样本空间上的两个随机变量。

定义：

设随机试验$E$的样本空间为$\Omega$，$X$和$Y$是定义在$\Omega$上的随机变量，由它们构成的向量$(X,Y)$，称为二维随机向量。

☁️ 分布函数

定义：

设$(X,Y)$是二维随机向量，对于任意实数$x,y$，称二元函数$$F(x,y)=P\{X\le x,Y\le y\}$$
为$(X,Y)$的分布函数。

PS:当然了，看到这里之前一定要先清楚了解随机变量的分布函数才行哦！快点击我复习一下

$F(x)$表示事件$P\{X\le x\}$发生的概率，那么$F(x,y)$表示的是什么呢？

先前说到用两个随机变量来表示平面上点的坐标，也就是两个随机变量所表示的事件一定要同时发生才行是吧，你想一下啊，如果随机变量$X$确定了，也就是$x$坐标确定了，如果$Y$没确定的话那么这个点就表示不出来。那么就有：

分布函数$F(x,y)$表示事件$\{X\le x\}$和事件$\{Y\le y\}$同时发生的概率。

如果我们就用$(X,Y)$来表示平面上随机点的坐标，那么分布函数$F(x,y)$在$(x_0,y_0)$处的函数值$F(x_0,y_0)$就是表示事件$P\{X\le x_0,Y\le y_0\}$发生的概率。在$xoy$面上表示的就是一块矩形面积，如下图：

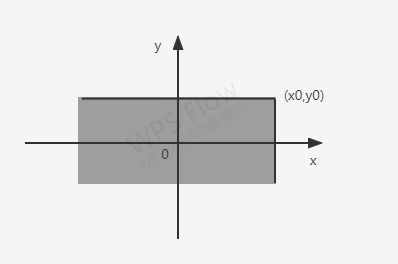
这个面积呢是无限向左下延伸的，大家自己动动脑袋想象一下噢！

如果这个还不能解释清楚随机向量的分布函数，那么别急，再来一个！

例如：对于$(X,Y)$落在矩形区域$\{(x,y):x_1<x\le x_2,y_1<y\le y_2\}$内的概率，先给出它在$xoy$面上的面积表示：
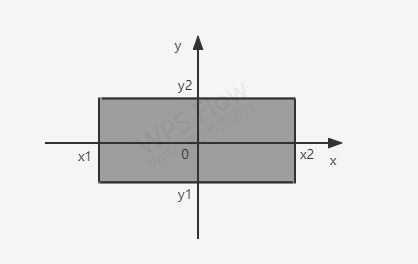
那么它的概率可表示为$$P\{x_1<X\le x_2,y_1<y\le y_2\}=F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1)$$
后面四个函数就相当于是在进行面积相加减，最后得到上图那个面积。

ok现在大致清楚了随机变量分布函数的概念，现在引入它的三个性质

☀️ 性质1

$F(x,y)$是变量$x,y$的不减函数（递增或者等于），也就是当$y$固定，$x_1<x_2$时，$F(x_1,y)\le F(x_2,y)$；当$x$固定，$y_1<y_2$时，$F(x,y_1)\le F(x,y_2)$。

☀️ 性质2

$0\le F(x,y)\le 1,-\infty <x<+\infty ,-\infty <y<+\infty$

分布函数的值就是概率噢

☀️ 性质3

对于固定的$y$，$$F(-\infty ,y)=\underset{x\to -\infty }{\lim }F(x,y)=0$$
对于固定的$x$，$$F(x,-\infty )=\underset{y\to -\infty }{\lim }F(x,y)=0$$
还有$$F(-\infty ,-\infty )=\underset{x,y\to -\infty }{\lim }F(x,y)=0$$
$$F(+\infty ,+\infty )=\underset{x,y\to +\infty }{\lim }F(x,y)=1$$
这里就需要大家用上面的面积法去想象一下噢。

二维离散型随机向量

如标题，如果一个二维随机向量是离散型的，那么它的每个分量都是离散型随机变量。

定义：

设二维离散型随机向量$(X,Y)$所有可能取得值为$(x_i,y_i),i=1,2,...,j=1,2,...$，记
$$P\{X=x_i,Y=y_i\}=p_{ij}i=1,2,...,j=1,2,...$$
称上式为二维离散型随机向量$(X,Y)$的概率分布或分布律。

也就是说，平面上一个点表示一个概率，这个点又由一个随机向量（两个随机变量）表示。

好了，知识总结完毕，接下来就是用C语言去实现做题的过程了。这期做题主要针对的就是二维离散型随机向量，因为二维连续型随机向量的指针点比较多，而且很多课后题也是针对于连续型的，所以下期就主要是对二维连续型随机向量进行知识点总结以及C语言实现。

C语言案例实现

1. 设有10件产品，其中7件正品，3件次品。现从中任取两次，每次取一件产品，取后不放回，求两次抽取的概率分布。

分析：这个题用条件概率也可以做，但这里我们就用随机向量来做。令$$X=\{\begin{array}{l}1，第一次取到的产品是次品\\ 0，第一次取到的产品是正品\end{array}$$
$$Y=\{\begin{array}{l}1，第二次取到的产品是次品\\ 2，第二次取到的产品是正品\end{array}$$
首先呢我们要写出$(X,Y)$所有可能取的值：$(0,0),(0,1),(1,1),(1,0)$。后面就用组合公式就可以算出概率了。代码如下：

#include 
#define M 90

// the algorithm of combination ——排列组合中组合的算法
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	
	return sum/p;
}
// the algorithm of abbreviation ——约分的算法
void Abbreviation(int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i < a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

// use structure to store the value of the Two-dimensioned vectors ——用结构体来存储二维向量的取值
typedef struct
{
	int X;
	int Y;
	// use an array to store the probability of the current vector ——用数组来存储当前向量表示的事件发生的概率
	// the reason why use an array is that we need to adapt to the abbreviation algorithm ——用数组的原因是为了与约分函数对应
	int p[2];
}TDVectors;

int main()
{
	TDVectors V[4];
	printf("Please input the values of X and Y:\n");
	for(int i = 0 ; i < 4 ; i++)
	{
		scanf("%d,%d",&V[i].X,&V[i].Y);
	}
	printf("The end of inputting-------------------\n");
	printf("The possible values of X and Y is :");
	for(int i = 0 ; i < 4 ; i++)
	{
		printf("(%d,%d) ",V[i].X,V[i].Y);
	}
	printf("\n");
	for(int i = 0 ; i < 4 ; i++)
	{
		// the number of quality goods ——正品的数量
		int z = 7;
		// the number of defective goods ——次品的数量
		int c = 3;
		V[i].p[0] = V[i].X == 0 ? Combination(z--,1) : Combination(c--,1);
		V[i].p[0] *= V[i].Y == 0 ? Combination(z,1) : Combination(c,1);
		// M denotes all the situations ——M表示所有的抽取情况
		V[i].p[1] = M;
	}
	// reduction of a fraction ——约分
	for(int i = 0 ; i < 4 ; i++)
		Abbreviation(V[i].p);
	for(int i = 0 ; i < 4 ; i++)
		printf("P{X=%d,Y=%d}=%d/%d\n",V[i].X,V[i].Y,V[i].p[0],V[i].p[1]);
	return 0;
}

为啥要在结构体数组再定义一个数组类型的成员变量，不麻烦吗？

别问，问就说是为了骚操作！

2. 为了进行吸烟与肺癌关系的研究，随机调查了23000个40岁以上的人，其结果如下表：

吸烟\肺癌	患	未患
吸	3	4597
不吸	1	18399

“3”表示既吸烟又患了肺癌的人数。后面的数字就不用解释了吧~~

分析：这个不同与正次品的判断，一眼看去，这啥呀，感觉好复杂~~

但实际上不然，对与这个题我们也可以引进二维随机向量$(X,Y)$来做，记
$$X=\{\begin{array}{l}1,被调查者不吸烟\\ 0,被调查者吸烟\end{array}$$
$$Y=\{\begin{array}{l}1,被调查者未患肺癌\\ 0,被调查者患肺癌\end{array}$$
然后嘛，这个题的做法就跟上面一样咯。代码也相差无几：

#include 
#define M 23000

// the algorithm of combination ——排列组合中组合的算法
int Combination(int n,int m)
{
	int sum = 1,p = 1;
	for( ; m > 0 ; m--)
	{
		sum *= n--;
		p *= m;
	}
	
	return sum/p;
}


typedef struct
{
	int X;
	int Y;
	float p;
}TDVectors;

int main()
{
	TDVectors V[4];
	int pos = 0;
	printf("Each variate has two possbible values,so there are four situations:");
	for(int i = 0 ; i < 2 ; i++)
	{
		for(int j = 0 ; j < 2 ; j++)
		{
			V[pos].X = i;
			V[pos].Y = j;
			pos++;
			printf("(%d,%d) ",i,j);
		}
	}
	printf("\n");
	printf("\n");
	printf("Now you need to input the number of each situation:\n");
	for(int i = 0 ; i < 4 ; i++)
	{
		scanf("%f",&V[i].p);
		printf("The situation(%d,%d) has %.0f people.\n",V[i].X,V[i].Y,V[i].p);
	}
	int All;
	printf("\n");
	printf("Please input the number of people in total:");
	scanf("%d",&All);
	for(int i = 0 ; i < 4 ; i++)
		V[i].p = V[i].p / All;
	printf("\n");
	for(int i = 0 ; i < 4 ; i++)
		printf("P{X=%d,Y=%d}=%.5f\n",V[i].X,V[i].Y,V[i].p);
	return 0;
}

不过有些地方还是做了一点点改动哈，一切都是为了更骚~

这期学习到这里就结束了噢。

咱们下期再见！