概率论与数理统计学习：随机向量（二）——知识总结与C语言实现案例

hello，大家好

这里是第七期概率论与数理统计的学习，我将用这篇博客去总结知识点以及用C语言实现案例的过程。

本期知识点：

1. 二维连续型随机向量

• 均匀分布
• 二维正态分布

2. 边缘分布

• 边缘分布函数
• 二维离散型随机向量的边缘概率分布
• 二维连续型随机向量的边缘概率密度

下面先总结知识点

二维连续型随机向量

上一期我们学习了二维离散型随机向量，那么这期就轮到连续型的啦。上一期

总所周知啊，连续型是一个区间的概率，离散型是一个一个点的概率~~那么先给出二维连续型随机向量的定义：

定义：

对于二维随机向量$(X,Y)$，$F(x,y)$是它的分布函数，若存在非负函数$f(x,y)$，使得对任意实数$x,y$，总有$$F(x,y)={\int }_{-\infty }^y{\int }_{-\infty }^{x}f(u,v)dudv$$
则称$(X,Y)$是二维连续型随机向量，称$f(x,y)$为二维连续型随机向量$(X,Y)$的概率密度函数，简称概率密度。

咦，等等，提问：为啥上式后面是$u,v$的函数？？？

一般来说肯定是这样的：${\int }_{-\infty }^y{\int }_{-\infty }^{x}f(x,y)dxdy$，前面积分上限的$x,y$表示的是一个具体的值，后面的$f(x,y)dxdy$中的$x,y$则是一个变量，所以为了更好地区别它们，所以把后面的$x,y$用$u,v$来替代。

☁️ 二维连续型随机向量的概率密度的性质

$f(x,y)\ge 0,-\infty <x<+\infty ,-\infty <y<+\infty$

${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(x,y)dxdy=1$

若$f(x,y)$在点$(x,y)$处连续，则有$\frac{{\partial }^{2}F(x,y)}{\partial x\partial y}=f(x,y)$

设平面$D$是平面上的任意区域，则点$(X,Y)$落在$D$内的概率$$P\{(X,Y)\in D\}=\int {\int }_{D}f(x,y)dxdy$$

最后一条性质很重要噢，它将二维连续型随机向量$(X,Y)$在平面区域$D$内取值的概率问题转化为一个二重积分的计算。从二重积分的几何意义可知，该概率在数值上等于以$D$为底，以曲面$z=f(x,y)$为顶面的曲顶柱体的体积。

不过忘了也不用太着急，在题中大多数也只是转化成在平面上的积分。

☁️ 均匀分布

定义：

设$D$是平面上的有界区域，其面积为$d$，若二维随机向量$(X,Y)$的概率密度函数为$$f(x,y)=\{\begin{array}{l}\frac{1}{d},(x,y)\in D\\ 0,其它\end{array}$$

则称$(X,Y)$服从$D$上的均匀分布，这个跟随机变量服从的均匀分布类似，用所占面积除以总面积即可。

☁️ 二维正态分布

定义：

设二维随机向量$(X,Y)$的概率密度函数为$$f(x,y)=\frac{1}{2\pi {\sigma }_1{\sigma }_2\sqrt{1-{\rho }^2}}{e}^{-\frac{1}{2(1-\rho {)}^2}[\frac{(x-{\mu }_1{)}^2}{{\sigma }_1^2}-2\rho \frac{(x-{\mu }_1)(y-{\mu }_2)}{{\rho }_1{\rho }_2}+\frac{(y-{\mu }_2{)}^2}{{\sigma }_2^2}]},-\infty <x<+\infty ,-\infty <y<+\infty$$

式中${\mu }_1,{\mu }_2$为实数，${\sigma }_1>0,{\sigma }_2>0,|\rho |<1$，则称$(X,Y)$服从参数为${\mu }_1,{\mu }_2,{\sigma }_1,{\sigma }_2,\rho$的二维正态分布，记作$(X,Y)$~$N({\mu }_1,{\mu }_2,{\sigma }_1^2,{\sigma }_2^2,\rho )$，同时称$(X,Y)$是二维正态随机向量。

emm…看看就好，看看就好…

边缘分布

☁️ 边缘分布函数

二维随机向量$(X,Y)$作为一个整体，具有分布函数$F(x,y)$，它们的分量$X$和$Y$都是随机变量，也有自己的分布函数，将它们分别记为$F(x)$和$F(y)$，依次称为$X$和$Y$的边缘分布函数。那么$F(x,y)$就称为$X$和$Y$的联合分布函数。

别太在意这个边缘与联合，它们都只是相对于彼此的一个名称而已。

边缘分布函数$F(x)$和$F(y)$都可以由$F(x,y)$确定：
$$F(x)=P\{X\le x\}=P\{X\le x,Y\le +\infty \}=F(x,+\infty )$$
$$F(y)=P\{Y\le y\}=P\{X\le +\infty ,Y\le y\}=F(+\infty ,y)$$

☁️ 二维离散型随机向量的边缘分布概率

离散型离散型，它表示一个一个点的概率，着重强调这个“点”嗷。

那么它的边缘概率分布是啥形式呢？

相当于先确定一个$X$，然后$P\{X=x_i\}$就表示它的概率，注意这里没有限制$Y$的取值，也就是说要把所有$Y$的全部取值都考虑进去。

也许结合一下“官方”知识更好理解一点呢：

设$(x,y)$是二维离散型随机向量，其概率分布为$$P\{X=x_i,Y=y_i\}=p_{ij}$$
那么$$P\{X=x_i\}=p_{i1}+p_{i2}+...+p_{ij}$$

同理，$$P\{Y=y_j\}=p_{1j}+p_{2j}+...+p_{ij}$$

怎样，懂否？

有了上面的基础，再给出它的定义

定义：

$$p_{i\cdot }=P\{X=x_i\}=\sum _j{p}_{ij},i=1,2,...$$
$$p_{\cdot j}=P\{Y=y_j\}=\sum _i{p}_{ij},j=1,2,...$$

分别称$p_{i\cdot }$和$p_{\cdot j}$为$X$和$Y$的边缘概率分布。bin~

别着急，还有一个小节的知识点！！

☁️ 二维连续型随机向量的边缘概率密度

这个有了前面的基础，我相信你们能够理解的

设$(X,Y)$是二维连续型随机向量，其概率密度函数为$f(x,y)$，由上一节可知
$$F(x)=F(x,+\infty )={\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{x}f(u,v)dudv={\int }_{-\infty }^x[{\int }_{-\infty }^{+\infty }f(u,v)dv]du$$

注意了噢（因为我在学的时候就没注意）

记$$f(u)={\int }_{-\infty }^{+\infty }f(u,v)dv(1)$$
（上式右边部分就是上上式那个$[]$中的那部分，需要跟上上式连起来一起思考！下式也一样！）

那么有$$F(x)={\int }_{-\infty }^{x}f(u)du(2)$$

那么此时此刻，恰如彼时彼刻，上式中的$f(u)$不就是$F(x)$的概率密度函数吗？$f(u)$的表达式如$(1)$，这样，我们就得到了二维连续型随机向量的概率密度。

好！又来一个定义

定义：

$$f(x)={\int }_{-\infty }^{+\infty }f(x,y)dy$$
$$f(y)={\int }_{-\infty }^{+\infty }f(x,y)dx$$
分别为$X$和$Y$的概率密度函数，！！！前提：$X,Y$都是连续型的随机变量。

呼~要结束了吧

真的真的只有最后一点了…

通过上面的内容，我们可以得到，对于服从矩形区域$D=\{(x,y):a\le x\le b,c\le y\le d\}$上均匀分布的$(X,Y)$，两个边缘概率密度分别为：
$$f(x)=\{\begin{array}{l}\frac{1}{b-a},a\le x\le b\\ 0,其它\end{array}$$

$$f(y)=\{\begin{array}{l}\frac{1}{d-c},c\le y\le d\\ 0,其它\end{array}$$

注意噢，这是对于矩形区域而言，对于其它区域上的均匀分布，不一定有上述结论！！

over over 啦！！！

C语言实现案例

1. 设二维随机向量$(X,Y)$的概率密度函数为$$f(x,y)=\{\begin{array}{l}a(6-x-y),0\le x\le 1,0\le y\le 2\\ 0,其它\end{array}$$
   1）确定常数a
   2）求$P\{X\le 0.5,Y\le 1.5\}$

分析：首先，做题是非常简单的，由二维连续型随机向量的概率密度函数的性质可知，${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(x,y)dxdy=1$。凭此就可求出$a$的值，然后第二问就是简单的换一下积分上下限即可。然而用代码实现起来却别有一番难度。下面先给出我自己写的代码，再做一些分析。
1）：

#include 
#include 
typedef struct
{
	int coe[2];		// coefficient of each item ——每一项的系数
	int X;			// the power of x of each item ——每一项中x的幂
	int Y;			// the power of t of each item ——每一项中y的幂
}Expre;

// Reduction of a fraction function ——约分函数
void Abbreviation(int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i < a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}

// The difference of fraction a and fraction b ——两个分数a、b的差
int* Differ(int* a,int* b)
{
	if(a[0] == 0)
	{
		b[0] *= -1;
		return b;
	}
	else if(b[0] == 0)
	{
		return a;
	}
	int t;
	t = a[1];
	a[1] *= b[1];
	a[0] *= b[1];
	b[1] *= t;
	b[0] *= t;
	a[0] -= b[0];
	Abbreviation(a);
	return a;
}

// The integral function ——积分函数
void Integral(Expre* ex,int* floor,int* ceil,char pos)
{
	if(pos == 'x')  // integrate x ——对x进行积分
	{
		printf("Please input the value of ceil:");		// 输入积分上限
		scanf("%d,%d",ceil,ceil + 1);
		printf("Please input the value of floor:");		//输入积分下限
		scanf("%d,%d",floor,floor + 1);
		for(int i = 0 ; i < 3 ; i++)
		{
			ex[i].X += 1;								// the power of x +1 ——x的幂加1
			ex[i].coe[1] *= ex[i].X;					// the coefficient divide the power of x ——系数再除以x的幂
			for(int j = 0 ; j < 2 ; j++)
				ceil[j] = pow(ceil[j],ex[i].X);			// put ceilling into the x ——将积分上限带入x
			for(int j = 0 ; j < 2 ; j++)
				floor[j] = pow(floor[j],ex[i].X);		// put floor into the x ——将积分下限带入x
			int* a = Differ(ceil,floor);                // calculate the difference of the values after we put ceil and floor into x ——计算带入值后积分上下限的差
			// then multiply the differenve with the coefficient of the item ——然后将这个差乘原来的系数
			ex[i].coe[1] *= a[1];
			ex[i].coe[0] *= a[0];
			Abbreviation(ex[i].coe);
			// we have embodied x,so we need to eliminate it ——因为我们已经对x进行积分了，所以后面的式子就没有x了
			ex[i].X = 0;
		}
	}
	else  			// integrate y ——对y进行积分
	{
		printf("Please input the value of ceil:");
		scanf("%d,%d",ceil,ceil + 1);
		printf("Please input the value of floor:");
		scanf("%d,%d",floor,floor + 1);
		for(int i = 0 ; i < 3 ; i++)
		{
			ex[i].Y += 1;
			ex[i].coe[1] *= ex[i].Y;
			for(int j = 0 ; j < 2 ; j++)
				ceil[j] = pow(ceil[j],ex[i].Y);
			for(int j = 0 ; j < 2 ; j++)
				floor[j] = pow(floor[j],ex[i].Y);
			int* a = Differ(ceil,floor);
			ex[i].coe[1] *= a[1];
			ex[i].coe[0] *= a[0];
			Abbreviation(ex[i].coe);
			ex[i].Y = 0;
		}
	}
}

// calculate a,the function changes with different conditions ——计算a，这个函数随着情况的不同而不同
void Calculate(Expre* ex)
{
	int a[2] = {12,1};
	for(int i = 1 ; i < 3 ; i++)
	{
		int t = a[1];
		a[1] *= ex[i].coe[1];
		a[0] *= ex[i].coe[1];
		ex[i].coe[1] *= t;
		ex[i].coe[0] *= t;
		a[0] -= ex[i].coe[0];
	}
	a[1] = a[0];
	a[0] = 1;
	Abbreviation(a);
	printf("The result is: a=%d/%d",a[0],a[1]);
}

int main()
{
	Expre ex[3];
	printf("Please input the values of coefficient and power of each item.\n"); // ——输入每一项的系数和x、y的幂
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("The NO.%d set of data is:",i + 1);
		scanf("%d,%d,%d,%d",&ex[i].coe[0],&ex[i].coe[1],&ex[i].X,&ex[i].Y);
	}
	printf("\n");
	printf("The polynomial is :\n");
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("%d/%d*a*x^%d*y^%d\n",ex[i].coe[0],ex[i].coe[1],ex[i].X,ex[i].Y);
	}
	printf("\n");
	int floor[2],ceil[2];
	char pos[2] = {'x','y'};				// pos denotes the one that you want to integrate ——pos表示你要对哪个变量积分
	Integral(ex,floor,ceil,pos[0]);			// the first integration ——第一次积分
	Integral(ex,floor,ceil,pos[1]);			// the second integration ——第二次积分
	printf("\n");
	printf("After the second integration,the polynimial is:\n");
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("%d/%d*a*x^%d*y^%d\n",ex[i].coe[0],ex[i].coe[1],ex[i].X,ex[i].Y);
	}
	printf("\n");
	Calculate(ex);
	return 0;
}

分析：

1. 积分：首先，这个题目涉及到对一个多项式的积分，说实话这个难度特别大。我想了又想也就想出了一个比较笨的方法。
   由于这个题只涉及到两个未知数（变量），所以我们可以把这个多项式的每一项分为3个部分：系数、x的幂、y的幂。然后用结构体来存储每一项的数据。
   积分也需要特别注意一下：

• 数学上的积分规则，本题就是一个幂函数，也就是每一次积分不只幂要增加，它的系数也要除以一个增加后的变量的幂。例如对于$x$，此时$X=1,a[0]=1,a[1]=1$。对它积分后，$\frac{1}{2}{x}^2$，则$X=2,a[0]=1,a[1]=1\ast X=2$。
• 积一次分后，也就是带入积分上下限并做了计算后，积分的那个变量的幂要置零，因为已经将具体的值带入那个变量去做计算了。

2. 系数：其次就是每一项的系数，为了更好地与题目相结合，我这里将系数都看作分数，用一个大小为2的整型数组来存储它，例如$a[0]=2,a[1]=3$就表示的是$\frac{2}{3}$，那么0呢就用$a[0]=0,a[1]=0$来表示。
3. 计算：由于相关计算都是对数组进行操作，针对的是分数，所以有点绕，不太直观。

2）：

#include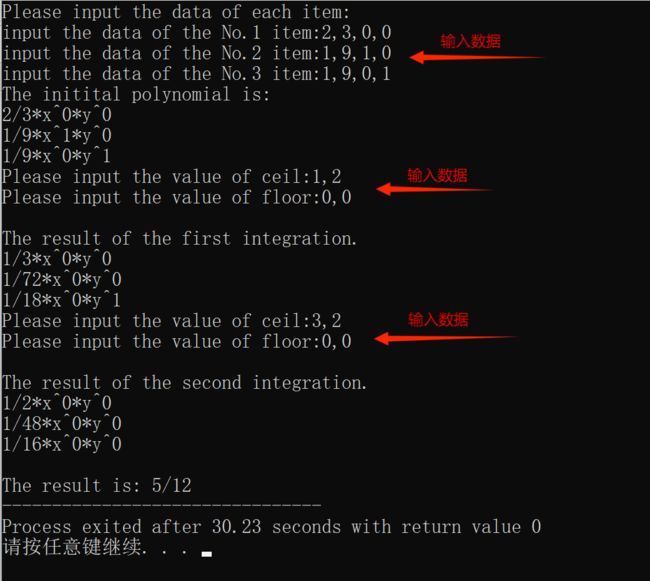 
#include 
typedef struct
{
	int coe[2];	
	int X;		
	int Y;			
}Expre;


void Abbreviation(int *a)
{
	while(a[0] % 2 == 0 && a[1] % 2 == 0)
	{
		a[0] /= 2;
		a[1] /= 2;
	}
	
	for(int i = 3 ;i <= a[1] / 2 ; i += 2)
	{
		while(a[0] % i == 0 && a[1] % i == 0)
		{
			a[0] /= i;
			a[1] /= i;
		}
	}
}


int* Differ(int* a,int* b)
{
	if(a[0] == 0)
	{
		b[0] *= -1;
		return b;
	}
	else if(b[0] == 0)
	{
		return a;
	}
	int t;
	t = a[1];
	a[1] *= b[1];
	a[0] *= b[1];
	b[1] *= t;
	b[0] *= t;
	a[0] -= b[0];
	Abbreviation(a);
	return a;
}


void Integral(Expre* ex,int* floor,int* ceil,char pos)
{
	if(pos == 'x')  
	{
		printf("Please input the value of ceil:");	
		scanf("%d,%d",ceil,ceil + 1);
		printf("Please input the value of floor:");	
		scanf("%d,%d",floor,floor + 1);
		for(int i = 0 ; i < 3 ; i++)
		{
			int a[2];
			int b[2];
			ex[i].X += 1;							
			ex[i].coe[1] *= ex[i].X;				
			for(int j = 0 ; j < 2 ; j++)
				a[j] = pow(ceil[j],ex[i].X);			
			for(int j = 0 ; j < 2 ; j++)
				b[j] = pow(floor[j],ex[i].X);		
			int* t = Differ(a,b);               
			ex[i].coe[1] *= t[1];
			ex[i].coe[0] *= t[0];
			Abbreviation(ex[i].coe);

			ex[i].X = 0;
		}
	}
	else  			
	{
		printf("Please input the value of ceil:");
		scanf("%d,%d",ceil,ceil + 1);
		printf("Please input the value of floor:");
		scanf("%d,%d",floor,floor + 1);
		for(int i = 0 ; i < 3 ; i++)
		{
			ex[i].Y += 1;
			ex[i].coe[1] *= ex[i].Y;
			for(int j = 0 ; j < 2 ; j++)
				ceil[j] = pow(ceil[j],ex[i].Y);
			for(int j = 0 ; j < 2 ; j++)
				floor[j] = pow(floor[j],ex[i].Y);
			int* a = Differ(ceil,floor);
			ex[i].coe[1] *= a[1];
			ex[i].coe[0] *= a[0];
			Abbreviation(ex[i].coe);
			ex[i].Y = 0;
		}
	}
}


int main()
{
	Expre ex[3];
	printf("Please input the data of each item:\n");
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("input the data of the No.%d item:",i + 1);
		scanf("%d,%d,%d,%d",&ex[i].coe[0],&ex[i].coe[1],&ex[i].X,&ex[i].Y);
	}
	printf("The initital polynomial is:\n");
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("%d/%d*x^%d*y^%d\n",ex[i].coe[0],ex[i].coe[1],ex[i].X,ex[i].Y);
	}
	int ceil[2],floor[2];
	char pos[2] = {'x','y'};
	Integral(ex,ceil,floor,pos[0]);
	printf("\n");
	printf("The result of the first integration.\n");
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("%d/%d*x^%d*y^%d\n",ex[i].coe[0],ex[i].coe[1],ex[i].X,ex[i].Y);
	}
	Integral(ex,ceil,floor,pos[1]);
	printf("\n");
	printf("The result of the second integration.\n");
	for(int i = 0 ; i < 3 ; i++)
	{
		printf("%d/%d*x^%d*y^%d\n",ex[i].coe[0],ex[i].coe[1],ex[i].X,ex[i].Y);
	}
	printf("\n");
	int* a = Differ(ex[0].coe,ex[1].coe);
	a = Differ(a,ex[2].coe);
	printf("The result is: %d/%d",a[0],a[1]);
	return 0;
}

第二问的代码大致一样，与第一问的差别也只是主函数上的一些差别。

☁️ 代码总结

这期主要是拓展了一下实现积分的思路，但仍有一下的局限性：

1. 只针对于幂函数
2. 积分上下限只能是某个具体的值，不能是关于一个变量的函数。例如${\int }_0^{1}dx{\int }_0^{-x+1}ydy$。其中积分后如何将$-x+1$带进去是一个待解决的问题
3. 系数的表示及相关运算太麻烦

若大家有什么意见，欢迎前来指正~

这期就到这里了，下期再见！

PS：这期案例为啥只有一个题？害，这一个题我可用代码写了好几天呢，咱就是说，够用就行！而且主要是锻炼咱写代码的思路，而不是非要每个题都用C去实现。